Dual Solutions of MHD Boundary Layer Flow of a Micropolar Fluid with Weak Concentration over a Stretching/Shrinking Sheet

Z.H.Khan,M.Qasim,Naeema Ishfaq,and W.A.Khan

Department of Mathematics,University of Malakand,Chakdara,Dir(Lower),Khyber Pakhtunkhwa,Pakistan

2Department of Mathematics,COMSATS Institute of Information Technology,Park Road,Chak Shahzad,Islamabad,Pakistan

3School of Mathematical Sciences,Peking University,Beijing 100871,China

4Department of Mechanical and Industrial Engineering College of Engineering,Majmaah University,Majmaah 11952,Kingdom of Saudi Arabia

1 Introduction

The boundary layer flows over a stretching surface are encountered in several engineering and industrial applications such as drawing of plastics, films and wires,crystal growing,continuous stretching,extrusion of polymer sheets,rolling and manufacturing plastic films and arti ficial fibers.In a melt spinning process,the extrudate from the die is generally drawn and simultaneously stretched into a sheet which is then solidi fied through quenching or gradually cooling by direct contact with water(Mahapatraet al.[1]).

In viscous fluid dynamics,the equations governing the flow are called Navier–Stokes equations. These equations are non-linear partial differential equations and exact analytical solutions corresponding to such equations are few.This is because of non-linearity regarding the inertial part of equations in the three-components of velocity,in some special situations,by means of appropriate transformations;the system of partial differential equations is reduced to that of non-linear ordinary differential equations,[2−10]which on few occasions can admit analytical solutions in closed form.[4−7]On the other hand,the resulting equations for flow of non-Newtonian fluids are more complicated and nonlinear with higher order than the Navier–Stokes equations.[11−12]Such complications in fact stem because of extra rheological parameters occurring in constitutive equations of non-Newtonian fluid.Unlike the NS equations the nonlinearity in the governing equations even for incompressible flow of non-Newtonian fluids not only appears in the inertial part but also in the viscosity,elasticity and viscoplastic parts.

The flow equation of micropolar fluid involves a microrotation vector in addition to classical velocity vector.In micropolar fluids,rigid particles in a small volume element can rotate about the centroid of the volume element.The micropolar fluids in fact can predict behavior at micro scale and rotation is independently explained by a microrotation vector.The fluid motion of the micropolar fluid is characterized by the concentration laws of mass,momentum and constitutive relationships describing the effect of couple stress,spin-inertia and micromotion.[13−17]Khanet al.[18]investigated boundary layer flow and heat transfer of a micropolar ferro fluid over a stretching surface.They considered microrotation of the ferroparticles and examined the effects of pertinent parameters on the dimensionless velocity,temperature,skin friction and Nusselt numbers for both weak and strong concentrations of ferro fluids.

Turkyilmazoglu[19]studied the flow of micropolar fluid and heat transfer past a porous shrinking sheet. He determined the bounds of multiple existing solutions and proved the presence of dual solutions for the flow field.Later,Turkyilmazoglu[20]obtained the dual solution for the flow due to a permeable stretching sheet.Besides this solution,dual solutions in the boundary layer flow of different fluids have been obtained by manyresearchers.[21−25]In this study,we obtained dual solutions for the heat transfer and flow of a micropolar fluid over stretching/shrinking sheet under the in fluence of the lf ow governing parameters.Closed-form exact solutions for the velocity,temperature and microrotation pro files are also obtained for the case of weak concentration.

2 Problem Formulation

2.1 Governing Equations

Consider the steady MHD boundary layer flow past a stretching/shrinking surface.It is assumed that sheet is stretched with a linearly velocityuw(x)=cx,wherecis a positive constant for stretching and negative for shrinking sheet.The governing boundary layer equations are

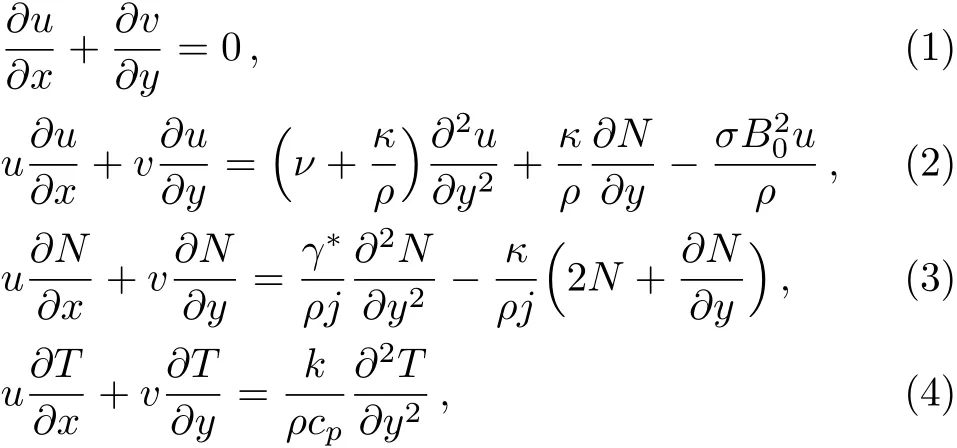
whereuandvare the velocity components parallel to thex-andy-axes,respectively,ρthe fluid density,νthe kinematic viscosity,Nthe microrotation or angular velocity,cpthe speci fic heat,kthe thermal conductivity of the fluid,j=(ν/c)is microinertia per unit mass,γ∗=(µ+κ/2)jandκare the spin gradient viscosity and vortex viscosity,respectively.

2.2 Boundary Conditions

The boundary conditions for the proposed model are

wherevwsurface mass transfer velocity withvw＜0 corresponds to suction andvw＞0 to injection velocity.

The boundary parameternin Eq.(6)varies in the range 0≤n≤1.Heren=0 corresponds to the situation when microelements at the stretching sheet are unable to rotate and denotes weak concentrations of the microelements at sheet.The casen=1/2 corresponds to the vanishing of anti-symmetric part of the stress tensor and it shows weak concentration of microelements and the casen=1 is for turbulent boundary layer flows.[13−15]

2.3 Similarity Transformations

In order to transform the governing partial differential equations into a system of non-linear ordinary differential equations,we introduce the following dimensionless and similarity variables into Eqs.(2)–(4)

Using the transformations in Eq.(8),the governing boundary layer equations can be written as

where primes denote differentiation with respect toη,Kis the microrotation parameter,Pris the Prandtl number,andMis the Hartman number.These parameters and dimensionless numbers are defined as follows

The transformed boundary conditions become

whereSis the suction/injection parameter andαis the stretching/shrinking parameter.The quantities of practical interest,are the local skin friction coeきcientCfx,and the local Nusselt numberNuxwhich are defined as

In dimensionless form,local skin friction coeきcient and the reduced local Nusselt can be written as

whereRex=ax2/νdenotes the local Reynolds number.

3 Method of Solution

3.1 Solution of Momentum Equation

For weak concentration i.e.,whenn=1/2,Eqs.(9)and(10)along with boundary conditions(13)and(14)has the exact solutions of the form

Substituting(17)in Eq.(9),we get

Solving Eq.(18)we have

Thus,the exact solution of Eq.(9)and(10)subject to the corresponding boundary conditions(13)and(14)are given by

The velocity pro file is determined after differentiating Eq.(20)once,

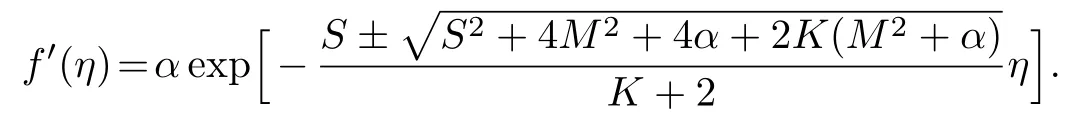
The skin friction coeきcient in closed form is obtained as

3.2 Solution of Energy Equation

To obtain the solution of Eq.(11),we introduce intermediate variableχas follows

Substituting(20)and(22)into Eq.(11),we get a secondorder decoupled boundary value problem

whereA=1 −Pr(α+βS)/β2and the corresponding boundary conditions take the form

Asχ=0 is the regular singular point of Eq.(22),we can apply the Frobenius method to seek an in finite power series solution of the form,

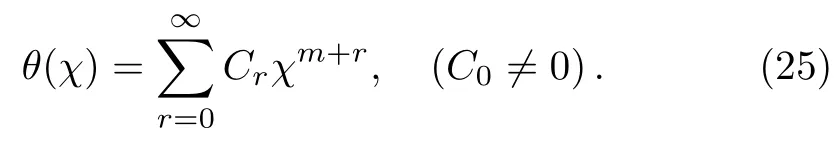
Differentiating(25)twice,we get

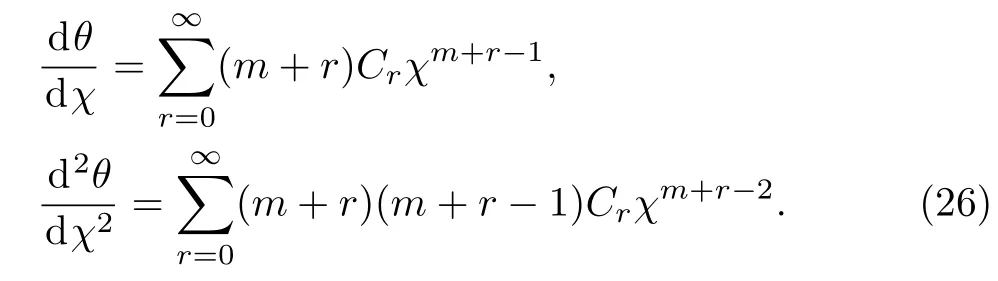
Substituting Eq.(26)in Eq.(23),we obtain

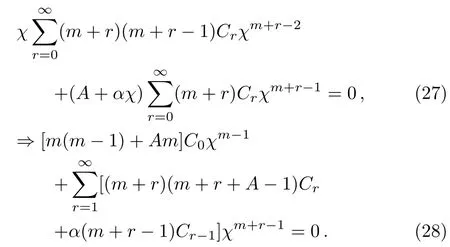
From Eq.(28),we get the indicial polynomial

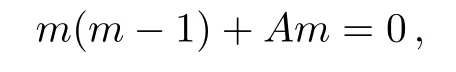
which is quadratic inmand having the indicial roots

From Eq.(28),the recurrence relation takes the form

Form=0,Eq.(29)becomes

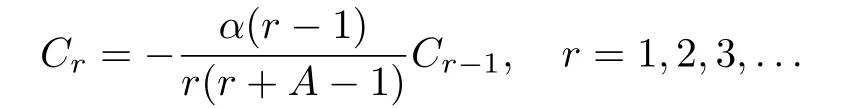
Above relation givesC1=C2= ···=Cr=0.Indicial rootm=0 gives constant solution,i.e.,θ1=constant.For the indicial rootm=1−Athe relation in Eq.(29)becomes

which on expanding gives

Using Pochhammer symbol,we can have

similarly,we can also have

Using the above so-called Pochhammer symbols,Eq.(30)takes the form

Hence the solution for indicial rootm=1−Abecomes

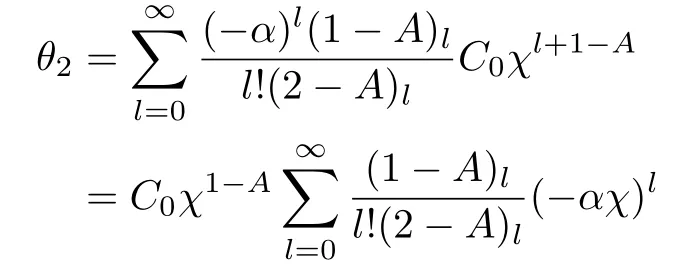
whereH(1−A,2−A,−αχ)is the con fluent hypergeometric function.Thus,the general solution of Eq.(25)is

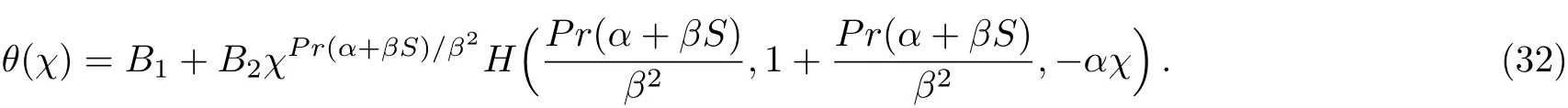
The boundary conditionθ(0)=0 givesB1=0 and the second boundary conditionθ(Pr/β2)=1 gives

Finally,substitutingB1,B2and the intermediate variableχin Eq.(32),we obtained the exact solution of energy equation

4 Results and Discussion

The solution domain forβis determined by different parameters,as shown in Figs.1 and 2.In each case,interesting behavior is observed.For the selected range of mass suction/injection,micropolar fluid parameter,stretching/shrinking parameters,and Hartman number,two solution branches(dual solutions)are found in each case.The characteristic polynomial of nonlinear boundary value problem possesses at least two distinct real roots.The upper branch corresponds to positive sign(+)and lower branch corresponds to negative sign(−)in Eq.(19).

Fig.1 The solution domain for β as function of(a)mass suction/injection parameter,S,(b)micropolar fluid parameter,K.

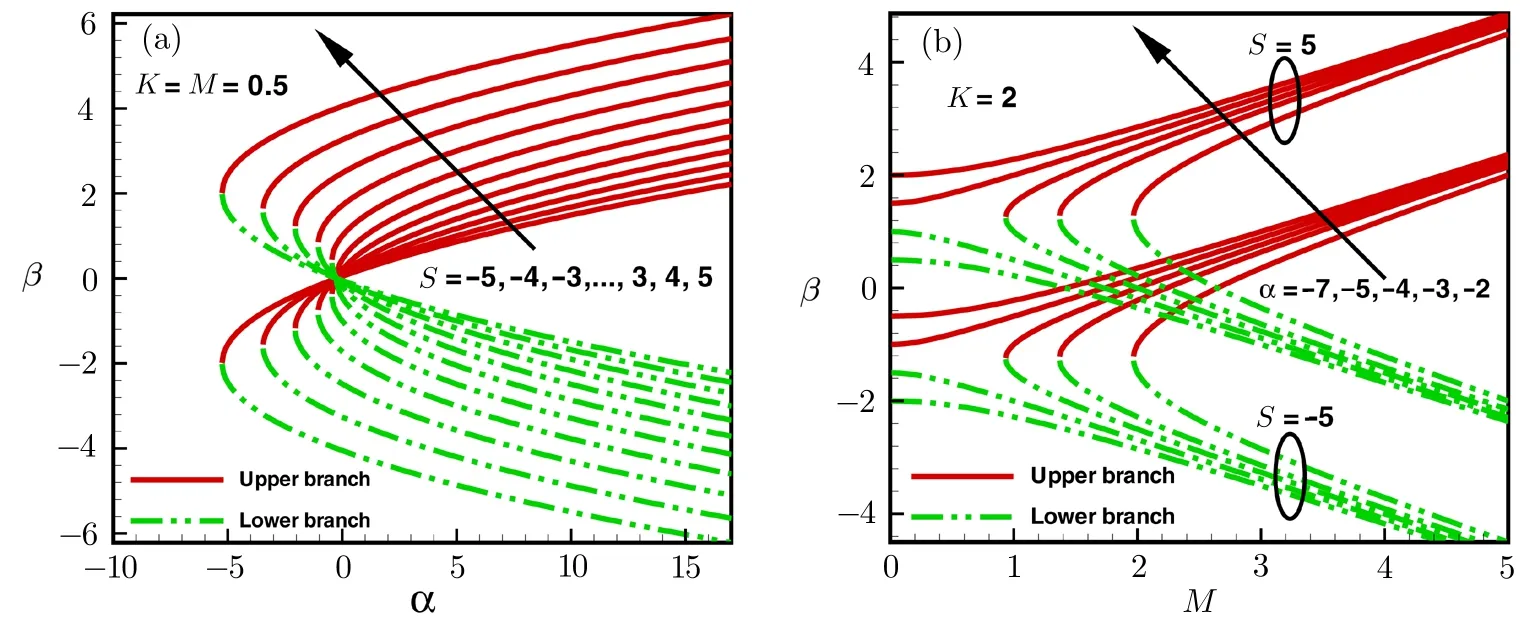
Fig.2 The solution domain for β as function of(a)stretching/shrinking parameter α and magnetic field parameter,M.

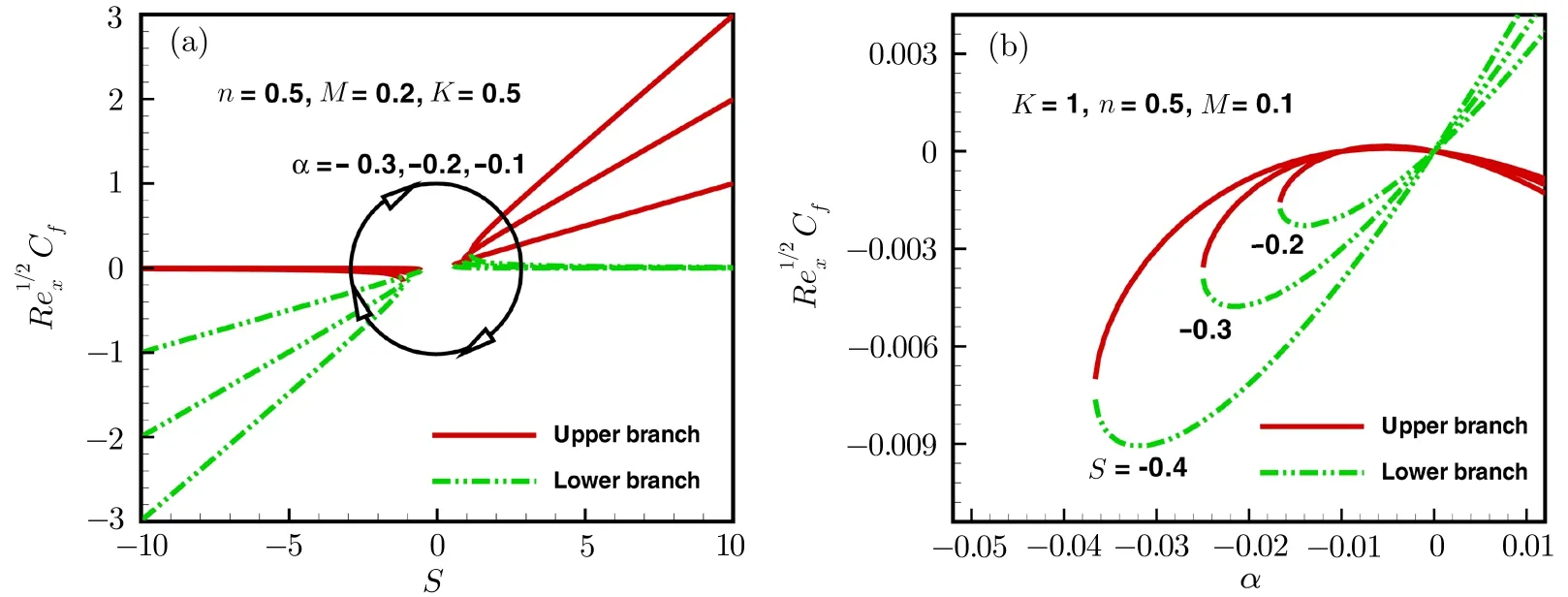
Fig.3 Variations of skin friction with suction/injection and stretching/shrinking parameters.

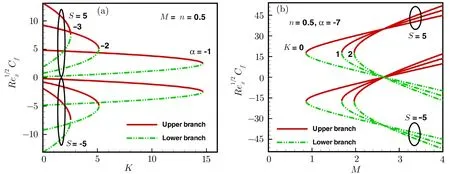
Fig.4 Variations of skin friction with microrotation fluid parameter and magnetic field parameter.

Fig.5 Variations of velocity pro files with suction and stretching/shrinking parameters.

Figures 3 and 4 illustrate the variations of skin friction coeきcient with different physical parameters.Skin friction coeきcient decreases by increasingα(for shrinking case).Further it is noticed that by increasing the velocity ratio parameters skin friction coeきcient increases for both upper and lower branch cases(Fig.3(a)).From Fig.4(a),it is noticed that the values of skin friction coeきcient are larger for the suction case as compared to injection case.This figure also shows that the skin friction coeきcient also increases by increasing the micropolar fluid parameterK.Skin friction coeきcient increases by increasing Hartman number for both suction and injection cases(Fig.4(b)).

Fig.6 Variations of velocity pro files with microrotation fluid parameter and magnetic field.

Fig.7 Variations of dimensionless microrotation pro file with suction and stretching/shrinking parameters.

Fig.8 Variations of dimensionless microrotation pro file with microrotation fluid parameter and magnetic field parameter.

The effects of suction,stretching/shrinking parameter on the dimensionless velocity(for shrinking case)are displayed in Figs.5(a)and 5(b)for both upper and lower branches.In the upper branch solution,suction parameter decreases the dimensionless velocity and thus the hydrodynamic boundary layer thickness decreases.The lower branch solution shows the opposite behavior.Similar,effects are observed from Fig.5(b)for the shrinking parameter on velocity.Figures 6(a)and 6(b)boundary layer thickness decreases by increasing the micropolar fluid parameter and Hartman number.The effects of microrotation parameter and Hartman number on the dimensionless velocity pro files are depicted in Figs.7(a)and 7(b)respectively.Figures 7(a)and 7(b)show that the behavior of micropolar fluid parameter and Hartman number are same.Inside the hydrodynamic boundary layer thickness,the effects of parameters are just opposite in both branch solutions.Boundary layer thickness increases by increasing the Harman number.Microrotation pro file decreases by increasing the microrotation fluid parameterKwhere as it increases by increasing the Hartman numberM.In Fig.9,Stream lines are plotted for different values ofS(for shrinking sheet).Flow pattern is different for upper branch case as compared to lower branch case.Figures 10 and 11 are plotted for the variation of local Nusselt number with stretching/shrinking,suction,Harman number and micropolar fluid parameter.Nusselt number increases by increasing the microrotation parameter(for both upper and lower branch).Further,we observed that Nusselt number is larger for the mass suction parameter.The effects of suction parameter,microrotation parameter and stretching/shrinking parameter on the dimensionless temperature are presented in Figs.12(a)and 12(b)respectively.The suction parameter reduces the dimensionless temperature within the thermal boundary layer,as shown in Fig.12(b)for both branch solutions.The same effect is observed for the stretching/shrinking parameter(Fig.13(a)).Thermal boundary layer increases by increasing the Hartman number(Fig.13(b)).

Fig.9 Streamlines for different values of Suction parameter(shrinking case).

Fig.10 Variations of Nusselt number with fluid flow parameters.

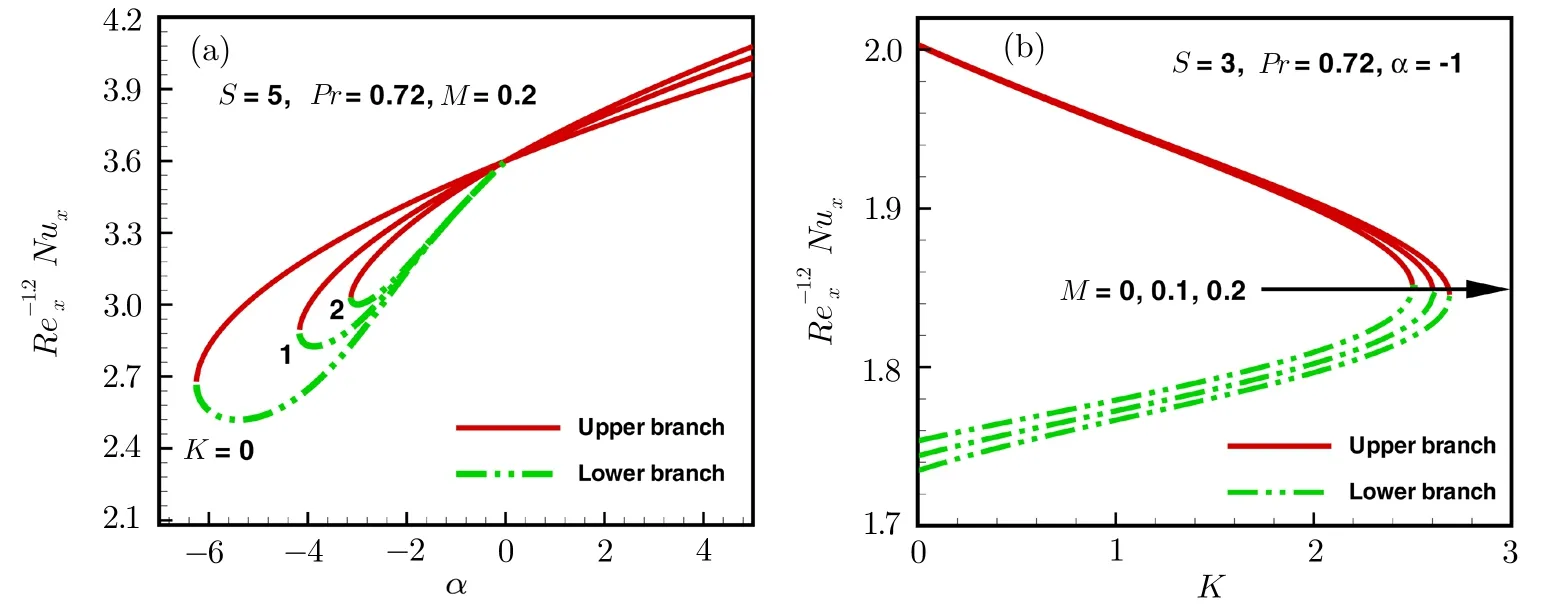
Fig.11 Variations of Nusselt number with fluid flow parameters.

Fig.12 Variations of temperature pro file with suction and microrotation fluid parameters.

Fig.13 Variations of temperature pro file with stretching/shrinking and magnetic field parameters.

5 Conclusions

In this paper,we have studied the dual nature of MHD micropolar fluid flow and heat transfer over stretching/shrinking under the in fluence of suction and injection.Exact solutions for velocity,temperature,skin friction and Nusselt number have been developed and discussed along with a detailed graphical visualization.We have shown that velocity,temperature pro files exhibits dual solutions for stretching/shrinking,suction/injection,micropolar fluid and magnetic field parameters.It is also observed that the suction and stretching/shrinking parameters reduce the dimensionless temperature within the thermal boundary layer,whereas the Hartman number increases both hydrodynamic and thermal boundary layer thickness and hence increases the overall resistance.

[1]T.R.Mahapatra,S.Dholey,and A.S.Gupta,Int.J.Non-Linear Mech.42(2007)4849.

[2]A.Ishak,R.Nazar,and I.Pop,Heat Mass Transf.44(2008)921.

[3]M.Z.Salleh,R.Nazar,and I.Pop,J.Taiwan Inst.Chem.Eng.41(2010)651.

[4]T.Fang and J.Zhang,Commun.Nonlinear Sci.Numer.Simul.14(2009)2853.

[5]S.Yao,T.Fang,and Y.Zhong,Commun.Nonlinear Sci.Numer.Simul.16(2011)752.

[6]T.Fang,S.Yao,and I.Pop,Int.J.Non-Linear Mech.46(2011)1116.

[7]M.Qasim,Alexandria Eng.J.52(2013)571.

[8]M.Qasim and S.Noreen,Eur.Phys.J.Plus 129(2014)1.

[9]S.Nadeem,R.Haq,and Z.Hayat,Alexandria Eng.J.53(2014)219–224.

[10]O.D.Makinde,W.A.Khan,and Z.H.Khan,Int.J.Heat Mass Transf.62(2013)526.

[11]Y.Lin,L.Zheng,X.Zhang,L.Ma,and G.Chen,Int.J.Heat Mass Transf.84(2015)903.

[12]Y.Lin,L.Zheng,and G.Chen,Powder Technol.274(2015)324.

[13]R.Nazar,N.Amin,D.Filip,and I.Pop,Int.J.Nonlinear Mech.39(2004)1227.

[14]A.Ishak,R.Nazar,and I.Pop,Can.J.Phys.84(2006)399.

[15]A.Ishak,R.Nazar,and I.Pop,Phys.Lett.A 372(2008)559.

[16]N.A.Yacob and A.Ishak,Meccanica 47(2012)293.

[17]M.Qasim,I.Khan,and S.Sha fie,PloS One 4(2013)e59393.

[18]W.A.Khan,Z.H.Khan,and M.Qasim,J.Nano fluids,5(2016)567.

[19]M.Turkyilmazoglu,Int.J.Heat Mass Transf.72(2014)388.

[20]M.Turkyilmazoglu,Int.J.Non-Linear Mech.83(2016)59.

[21]K.Bhattacharyya,Int.J.Heat Mass Transf.7(2011)917.

[22]N.S.Akbar,S.Nadeem,R.Ul Haq,and S.Ye,Ain Shams Eng.J.5(2014)1233.

[23]S.V.Subhashini and R.Sumathi,Int.J.Heat Mass Transf.71(2014)117.

[24]M.A.El-Aziz,Journal of the Egyptian Mathematical Society 24(2016)479.

[25]N.Freidoonimehr and A.B.Rahimi,Adv.Powder Technol.28(2016)685.