Higgs and Single Top Associated Production at the LHC in the Left-Right Twin Higgs Model∗

Xing-Yu Jiang(蒋兴雨),Jin-Zhong Han(韩金钟), Guang Yang(杨光),and Chun-Xu Yu(喻纯旭)School of Physics,Nankai University,Tianjin 300071,China

2School of Physics and Electrical Information,Shangqiu Normal University,Shangqiu 476000,China

3School of Physics and Telecommunications Engineering,Zhoukou Normal University,Zhoukou 466001,China

4Basic Teaching Department,Jiaozuo University,Jiaozuo 454000,China

1 Introduction

After the discovery of the Higgs boson at the Large Hadron Collider(LHC),it is always one of the forefront topics and has been studied heatedly.In order to ultimately establish its nature,a precise measurement of the Higgs couplings is needed at current and future LHC runs.One of the important contents is the Yukawa coupling,which can play a key role in testing the Standard Model(SM)and probing the new physics.In the SM,the Yukawa couplings of fermions to the Higgs boson are proportional to their masses.Being the heaviest particle,the top quark owns the strongest Yukawa coupling so that it has the preference to reveal the electroweak symmetry breaking(EWSB)mechanism and new physics.

As a necessary supplement to thethproduction,the Higgs boson in association with a single top quark production contains the important relative phase information on the couplings of the Higgs toWboson and to top quark.[1]The production processes can be conveniently classi fied in three main channels:(i)t-channel,where theWis spacelike;(ii)s-channel,where theWis timelike;(iii)W-associated,where theWis on-shell.In some new physics models,the couplings of the Higgs boson and the single top quark can be generated at tree level,or enhanced to observable levels through radiative corrections,many relevant works have been carried out extensively.[2]

To solve the so-called hierarchy or fine-tuning problem of the SM,the left-right twin Higgs(LRTH)model was proposed.[3]The LRTH model is a concrete realization of the twin Higgs mechanism,[4]which can be implemented with the discrete symmetry being identi fied with left-right symmetry.The LRTH model predicted some new particles,such asWH,T,ϕ±,they can contribute to the Higgs production processes.Besides,some Higgs couplings with respect to the SM are changed.As a result,the Higgs properties in the LRTH model is different from the SM Higgs.So,the studies of various Higgs production and decay can provide a good opportunity to test the LRTH model.[5]

In this work,we focus on the production of a Higgs boson in association with a single top quark at 8(14)TeV LHC in the LRTH model.This paper is organized as follows.In Sec.2 we brie fly review the basic content of the LRTH model related to our work.In Sec.3 we study the cross sections of the three production channels and show the numerical results.Finally,we give a summary in Sec.4.

2 Left-Right Twin Higgs Model

In the LRTH model,the SM symmetry is extended to SU(2)L×SU(2)R×U(1)B−L,which is embedded into a global U(4)×U(4)symmetry.The twin symmetry is identi fied as the left-right symmetry which interchangesLandR,implying that the gauge couplings of SU(2)Land SU(2)Rare identical(g2L=g2R=g2).Two Higgs fields,Hand,are introduced and each transforms as(4,1)and(1,4),respectively.After the two Higgs obtain vacuum expectation values(VEVs)〈H〉=(0,0,0,f)and〈〉=(0,0,0,),the global symmetry U(4)breaks down to U(3),and SU(2)R×U(1)B−Lbreaks down to the SM U(1)Y.Three Goldstone bosons are eaten by the massive gauge bosonsZHandW±H,while the rest fourteen contain the SM SU(2)LHiggs doublet fromHL,an extra SU(2)LHiggs doublet fromL,a neutral real pseudoscalarϕ0and a pair of charged scalar fieldsϕ±.

The masses for the heavy gauge bosons and scalars are given by

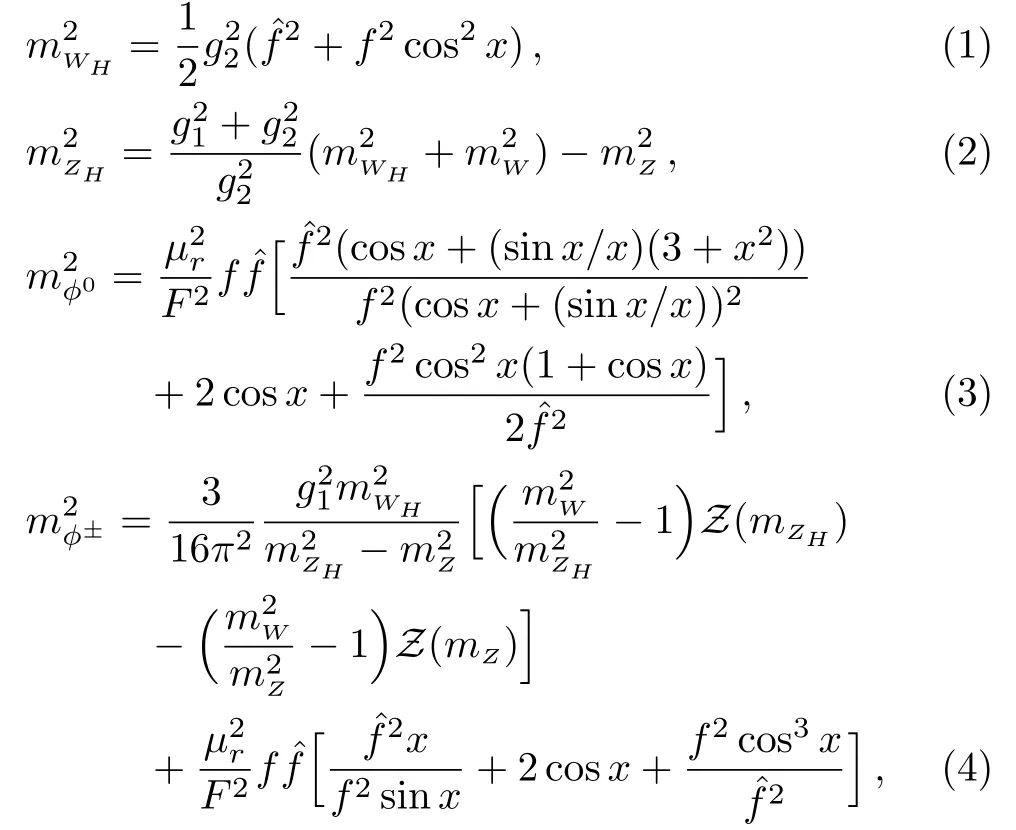
In order to cancel the one-loop quadratic divergence of Higgs mass induced by top quark,a heavy top quark partnerTis introduced.Their masses are given by

The new vertices related to our calculations are given as follows:[6]

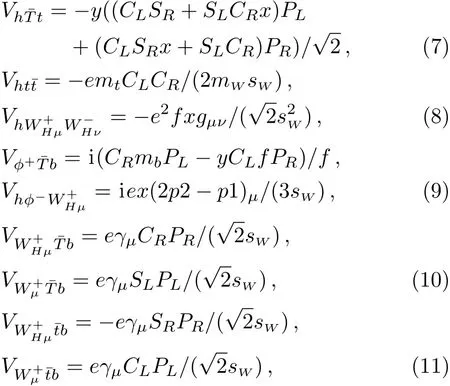
where

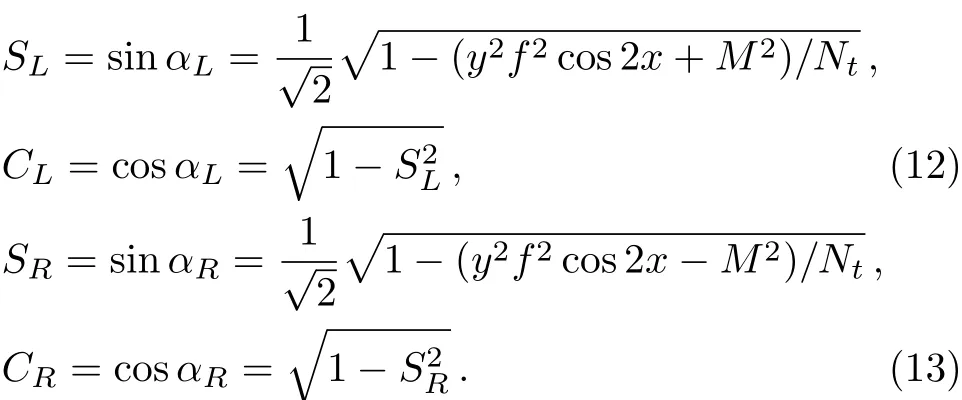
3 Numerical Results and Discussions

As shown in Figs.1–3,the Higgs boson in association with a single top quark can be produced at the LHC throught-channel,s-channel,andW-associated channel.In comparison with the SM,we can see that the Feynman diagrams receive the additional contributions arising from the heavy gauge bosonsWH,the charged Higgs bosonsϕ±and the heavy top quarkT.In our calculations,the conjugate processes have been considered,unless stated otherwise.

Fig.1 Feynman diagrams for pp→thj in the LRTH model at tree level.

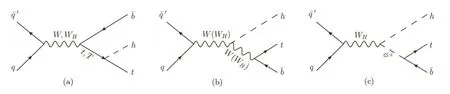
Fig.2 Feynman diagrams for pp → th in the LRTH model at tree level.

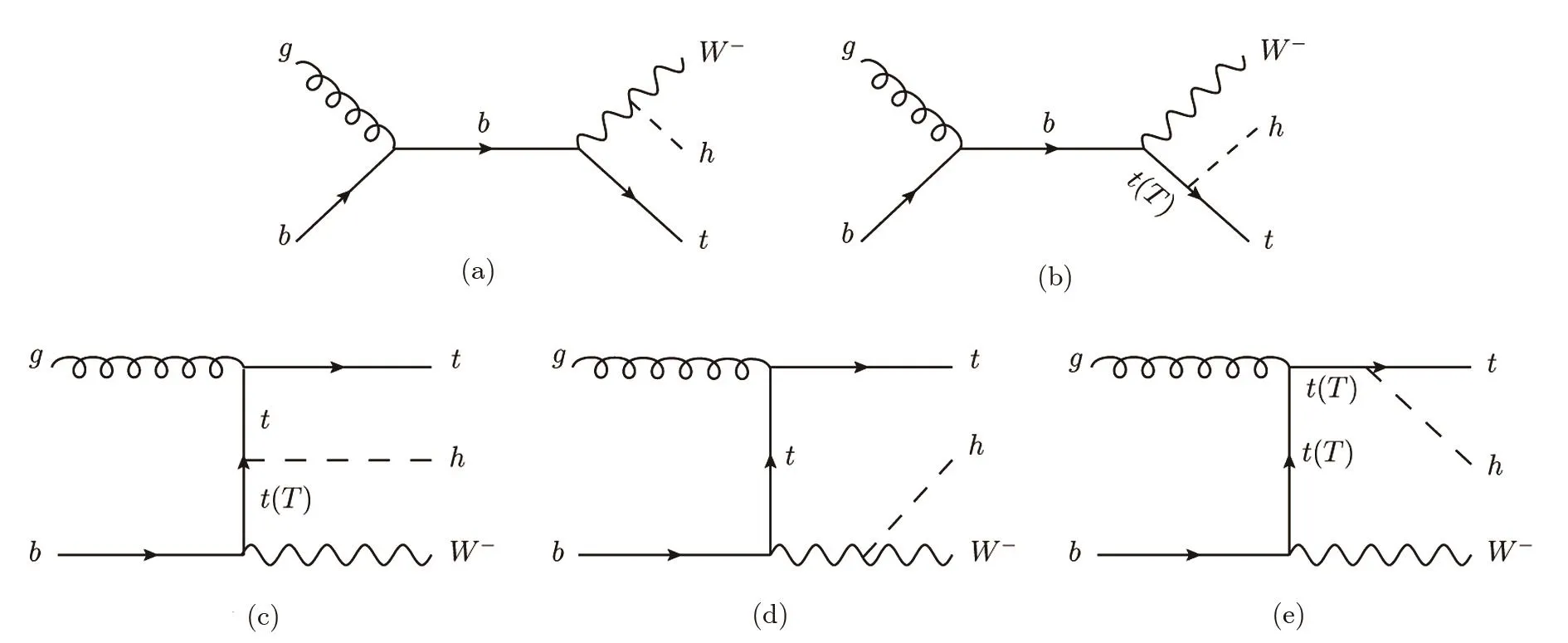
Fig.3 Feynman diagrams for pp→thW−in the LRTH model at tree level.

In our calculations,we use CalcHEP3.6.25[7]to compute the tree-level production cross sections.We take CTEQ6L as the parton distribution function(PDF)[8]and set the renormalization scaleµRand factorization scaleµFto beµR=µF=mt+mh.The SM input parameters are taken as follows:[9]

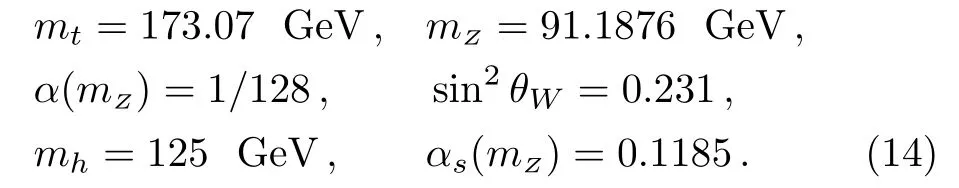
For the LRTH model parameters,there are three parametersf()andMare involved in the amplitudes.The parametercan be determined by requiring that the SM Higgs boson obtains an EWSB VEV of 246 GeV.Considering the current constrains,[10]we take the scalefin the range of 500 GeV≤f≤1500 GeV andM=150 GeV.

In Fig.4(a),we show the production cross sectionσthjat 8(14)TeV LHC as a function of the scalefforM=150 GeV.When the scalefis small,the on shell decayT→tharising from Fig.1(b)dominates the single top production process so that the cross sectionσthjis enhanced sizably.The maximum of the cross section can reach 22 fb(108 fb)for 8(14)TeV LHC,which deviates from its SM value obviously.To be clear,we also show the production cross sectionσT−thjof the subprocess only included heavy topTat 8(14)TeV LHC as a function of the saclefforM=150 GeV in Fig.4(b).Due to the branching ratio of the decayT→thdecreases quickly for largermT(this corresponds to the larger scalef),the production cross sectionσT−thjdecreases with the increasing scalef,[6]so that the other negative contribution will dominate at the high scalef.The cross sections of the processpp→thjtend to the SM values with the increasing scalef,which indicates that the effects of the LRTH model will decouple at the high scalef.

In Fig.5(a),we show the production cross sectionσthbat 8(14)TeV LHC as a function of the scalefforM=150 GeV.From Fig.2,we can see that the processpp→thcan be produced vias-channelWorWHexchange at the LHC.SinceWHis heavier thanTin the LRTH model,thes-channel on shell decayWH→T(→th)from Fig.2(a)dominates this production process so that the cross section can be enhanced sizably.For clarity,we also show the production cross sectionσT−thbof the subprocess only included heavy topTat 8(14)TeV LHC as a function of the saclefforM=150 GeV in Fig.5(b).We can see that the branching ratios of the heavy topTdecreases quickly with the increasing scalef,so that thepp→thproduction cross section decreases.Besides,we can see that the effects of the LRTH model decouple in the processpp→that the high scalef.

Recently,the CMS collaboration has searched for massiveWHresonances for several new physics models at 8 TeV and 13 TeV LHC.[11]Considering the conservative limit from the little Higgs model,the heavy gauge bosonWHwith masses lower than 1.4 TeV are excluded,which correspond to the limitf＞600 GeV.Besides,The CMS collaboration has performed searches for thetHqproduction withκt= −1 in multiple decay channels of the Higgs boson.[12]but it will hardly exclude the parameter space.Under this constraint,we can see that the cross sectionσthbcan be enhanced to 40 fb(160 fb)for 8(14)TeV LHC,which has already exceeded the production cross section of the processpp→thj.

Same as above,we show the production cross sectionσthWand the production cross sectionσT−thWof the subprocess only included heavy topTat 8(14)TeV LHC as a function of the scalefforM=150 GeV in Figs.6(a)and 6(b),respectively.We can see that the LRTH production cross sections are less than the relevant SM values,this is because the contribution arising from the heavy topTis weak in this process.

Fig.4 The dependence of the σthjat 8(14)TeV LHC on the scale f in the LRTH model.

Fig.5 Same as Fig.4,but for the σthb.

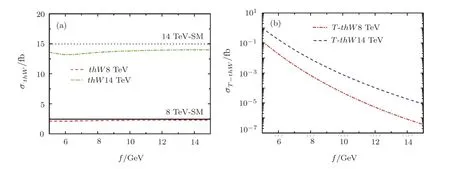
Fig.6 Same as Fig.4,but for the σthW.

In Fig.7,we display the normalized transverse momentum distributions of thethfinal state particles and the normalized invariant mass distributionMhtin the SM and the LRTH for the scalef=800 GeV at 14 TeV LHC.We can see that the transverse momentum distributions of the final state particles move towards the high energy region due to the effect of the heavy particles.The invariant mass distributionMhthas a peak at∼mT,which is caused by thes-channel on shell decayT→thfrom Fig.2(a).Since these differential distributions of the final state particles in the LRTH model are very different from that in the SM,we can use them to distinguish the SM and the LRTH signals at the LHC.

For the processpp→th,requiring a semileptonic top and the decayh→bleads to the signal 4b+l±+E/T.For this signal,tZwith decayZ→bandtbare two of the main backgrounds.Due to the large rate oftandtj,when bothcandsquarks from the hadronically decayingWare mistagged,these processes will be the dominant backgrounds. In order to investigate the observability of the processpp→th,a detailed signal-to-background analysis by the Monte Carlo simulations will be needed.

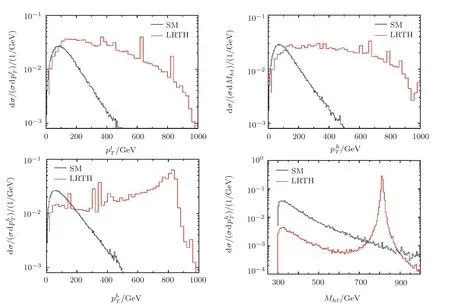
Fig.7 Normalized distributions of pp → th at 14 TeV LHC in SM and LRTH for f=800 GeV.

4 Summary

In this work,we investigated the production of the Higgs boson associated a top quark at the LHC.We find that the LRTH effect is obvious in the region with small scalef,especially for the processpp→th.If these effects are indeed observed in the future,then it would require further analysis to identify the reason responsible for the enhancement as well as a realistic model that can contribute to the enhancement of the production cross sections.If no evidence is found for an excess,it will give stringent limit to the LRTH model.

[1]G.Bordes and B.van Eijk,Phys.Lett.B 299(1993)315;A.Ballestrero and E.Maina,Phys.Lett.B 299(1993)312;W.J.Stirling and D.J.Summers,Phys.Lett.B 283(1992)411;J.L.Diaz-Cruz and O.A.Sampayo,Phys.Lett.B 276(1992)211.

[2]V.Barger,M.McCaskey,and G.Shaughnessy,Phys.Rev.D 81(2010)034020;M.Farina,C.Grojean,F.Maltoni,E.Salvioni,and A.Thamm,J.High Energy Phys.1305(2013)022;L.Wu,J.High Energy Phys.1502(2015)061;A.Kobakhidze,L.Wu,and J.Yue,J.High Energy Phys.1410(2014)100;A.Greljo,J.F.Kameni,and J.Kopp,J.High Energy Phys.1407(2014)046;S.Khatibi and M.M.Najafabadi,Phys.Rev.D 89(2014)054011;D.Atwood,S.K.Gupta,and A.Soni,J.High Energy Phys.1410(2014)57;L.Feng and Z.F.Kang,J.Cosmol.Astropart.Phys.1310(2013)008;Y.Wang,F.P.Huang,C.S.Li,B.H.Li,D.Y.Shao,and J.Wang,Phys.Rev.D 86(2012)094014;J.Chang,K.Cheung,J.S.Lee,and C.T.Lu,J.High Energy Phys.1405(2014)062;B.F.Yang,J.Z.Han,and N.Liu,J.High Energy Phys.04(2015)148;Y.M.Zhang and B.F.Yang,Europhys.Lett.110(2015)21001;F.Demartin,F.Maltoni,K.Mawatari,and M.Zaro,Eur.Phys.J.C 75(2015)267;John Campbell,R.Keith Ellis,and Raoul Röntsch,Phys.Rev.D 87(2013)114006;P.Agrawal,S.Mitra,and A.Shivaji,J.High Energy Phys.1312(2013)077;B.F.Yang,Z.Y.Liu,J.Z.Han,and G.Yang,Adv.High Energy Phys.2016(2016)2613187.

[3]Z.Chacko,H.S.Goh,and R.Harnik,J.High Energy Phys.01(2006)108.

[4]Z.Chacko,H.S.Goh,and R.Harnik,Phys.Rev.Lett.96(2006)231802;Z.Chacko,Y.Nomura,M.Papucci,and G.Perez,J.High Energy Phys.01(2006)126;R.Foot and R.R.Volkas,Phys.Lett.B 645(2007)75;A.Falkowski,S.Pokorski,and M.Schmaltz,Phys.Rev.D 74(2006)035003;S.Chang,L.J.Hall,and N.Weiner,Phys.Rev.D 75(2007)035009.

[5]L.Wang and J.M.Yang,J.High Energy Phys.1005(2010)024;L.Wang and X.F.Han,Nucl.Phys.B 850(2011)233;L.Wang,L.Wu,and J.M.Yang,Phys.Rev.D 85(2012)075017;W.Ma,C.X.Yue,and T.T.Zhang,Chin.Phys.C 35(2011)333;W.Ma,C.X.Yue,and Y.Z.Wang,Phys.Rev.D 79(2009)095010;Y.B.Liu and Z.J.Xiao,J.Phys.G 42(2015)065005;J.Z.Han,S.F.Li,B.F.Yang,and N.Liu,Nucl.Phys.B 896(2015)200;J.Z.Han and B.Z.Li,Commun.Theor.Phys.60(2013)205;J.F.Shen,Y.B.Liu,H.Zhao,and J.Cao,Commun.Theor.Phys.54(2010)701.

[6]H.S.Goh and S.Su,Phys.Rev.D 75(2007)075010.

[7]A.Belyaev,N.Christensen,and A.Pukhov,Comput.Phys.Commun.184(2013)1729.

[8]J.Pumplin,D.R.Stump,J.Huston,H.L.Lai,P.M.Nadolsky,and W.K.Tung,J.High Energy Phys.0207(2002)012.

[9]K.A.Olive,et al.,(Particle Data Group),Chin.Phys.C 38(2014)090001.

[10]Y.B.Liu,S.Cheng,and Z.J.Xiao,Phys.Rev.D 89(2014)015013.

[11]CMS Collaboration,Eur.Phys.J.C 76(2016)237.

[12]CMS Collaboration,CMS PAS HIG-14-015(2014);J.High Energy Phys.06(2016)177;CMS PAS HIG-14-001(2014);CMS PAS HIG-14-026(2015).