A Simple Method on Generating any Bi-Photon Superposition State with Linear Optics∗

Ting-Ting Zhang(张婷婷),Jie Wei(魏杰),and Qin Wang(王琴),3,†1Institute of Signal Processing and Transmission,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

2Key Laboratory of Broadband Wireless Communication and Sensor Network Technology,Nanjing University of Posts and Telecommunications,Ministry of Education,Nanjing 210003,China

3Key Laboratory of Quantum Information,CAS,University Science and Technology of China,Hefei 230026,China

1 Introduction

The coherent superposition state plays an important role in the field of quantum information[1−3]and quantum computing.[4−6]In the past few decades,plenty of experimental and theoretical work have been carried out on the generation of superposition states,such as the generation of the eight-photon GHZ states,[7−8]the spin-motion entanglement in a trapped ion,[9]the generation and observation of the micro-macro entanglement state with linear optics,[10−11]and the generation of hybrid entanglement of light.[12]Up to today,many kinds of approaches have been proposed on generating coherent superposition states with either continuous or discrete variables[13−14]through both linear and nonlinear optics.[15−17]However,among them most are either limited on generating certain speci fic states,[8]or con fining to the superposition of single photons.[18−19]

In this paper,we present a simple method on generating any given bi-photon superposition state state,i.e.,c0|0〉+c1|2〉,by making use of the entangling property of a beam-splitter(BS)and the post-selection characteristics of threshold single-photon detectors.In the scheme,a bi-photon Fock state(|2〉)and a two-mode squeezed state(|β〉)incident on two input channels of a BS,generating the temporo-spatial mode entangled output states.When a quantum measurement is performed on one of the output channels,the other one will collapse to certain ensemble.Our work is to characterize the post-selected ensemble and demonstrate that we can obtain any superposition state of|0〉and|2〉by modulating the initial conditions.During this process,the two-mode squeezed state(|β〉)works as a seed state,and the input bi-photon Fock state(|2〉)can be seemed as quantum-optical catalysis,[11]because itself keeps unchanged after this transformation.While the resulting signal state will show drastic difference from the original seed state(|β〉).

Besides,it is required both the intensity of the seed state(β)and the transmission rate of the beam-splitter(t)are very weak(β∼t2≪1)in this scheme.The seed state can be approximated as|β〉=|0〉+β|2〉.When a two-mode squeezed state and a bi-photon state meet on the input channels of a beam-splitter,via performing biphoton projection measurement on one(“idler”)of the two output channels,the other(“signal”)one will collapse to:

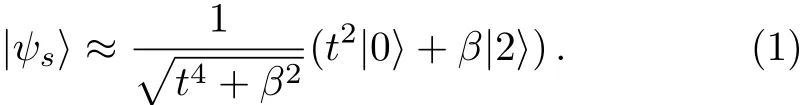
Although the generated quantum state has the similar elements as the primary input state,the arbitrary amplitude of|0〉and|2〉can be controlled by manipulating the ratio betweenβandt2.Obviously,by reducing the value oftor increasing the size ofβ,it will perform a gradual transition between the classical(|0〉)to the nonclassicalstate(|2〉).In this sense,we can take it as a bridge between the particle and the wave aspects of the electromagnetic field,and thus similar to a bi-photon “Schrödinger-Cat-like State”.

The outline of the paper is organized as follows:In Sec.2,we introduce detailed scheme on generating the superposition state and present corresponding theory on taking practical experimental conditions into account,e.g.,imperfect seed state and non-ideal single-photon detectors.In Sec.3,we carry out corresponding numerical simulations and calculate both the Wigner function and the state fidelity of the final states.Finally,discussions and conclusions are given out in Sec.4.

2 The Theory on Generating any Bi-photon Superposition State

In this section,we introduce the detailed scheme on how to generate any superposition state of|0〉and|2〉and explore its performance under either ideal or realistic experimental conditions.The schematic of the experimental setup is displayed in Fig.1.It mainly consists of two parts,i.e.,the state preparation and the state characterization.First,a bi-photon state|2〉and a two-mode squeezed state|β〉simultaneously incident on the two input channels of the beam-splitter(BS1),resulting an entangled state in the two output modes,one is idler mode,and the other is signal mode.After doing post-selection measurement on the idler mode,the signal mode will collapse to certain ensemble.Wherein the post-selection process can be realized by applying two-photon coincidence measurement,made up of one beam-splitter(BS2)and two single-photon detectors(D1 and D2).The state characterization can be accomplished by utilizing a balanced homodyne detection,see the right side of Fig.1.

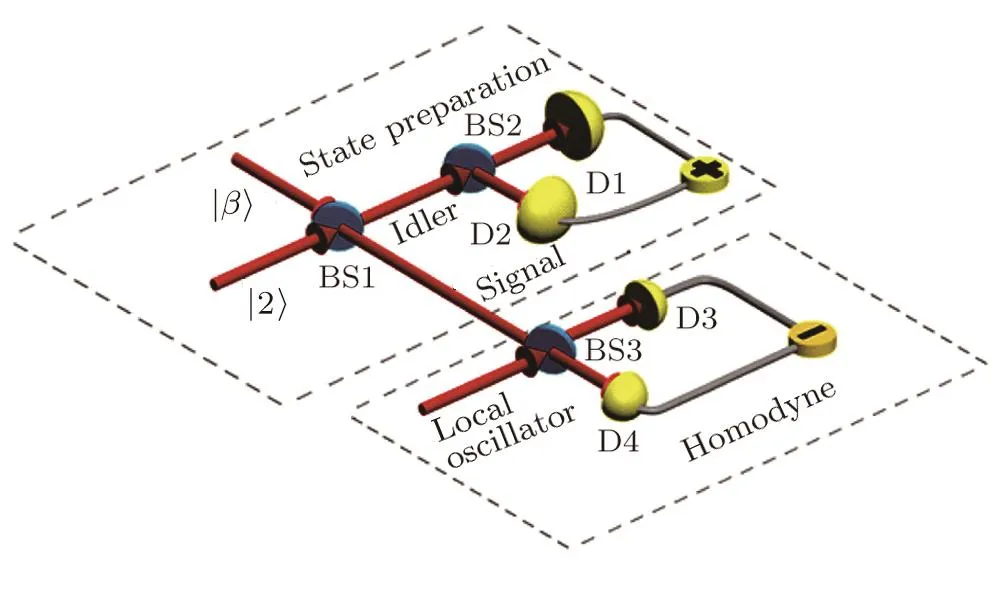
Fig.1 (Color online)The schematic experimental setup of generating the superposition state of|0〉and|2〉.It includes the state preparation part and the state characterization part.BS1∼BS3:beam-splitters.D1∼D4:single-photon detectors.

In the scheme,the input states,|2〉and|β〉,each can be generated by spontaneous emission of bi-exitons in quantum dots or parametric down-conversion process with nonlinear crystal.Below let us start from assuming the preparation of|2〉and|β〉are ideal.When they mix on two input arms of a beam-splitter,the entangled output state can be found by the BS generator:[18]

where

Herer2=1−t2is the BS re flectivity andare binomial coeきcients.

In present commercial single-photon detector,it has a“click”as long as photons(the photon numbern≥1)incident on its sensitive area,which is called the threshold single-photon detector.In our experiment,we use two such kinds of threshold single-photon detectors for coincidence measurement,i.e.,the two detectors“click” simultaneously.It can be described by the following positive operator-valued measurement(POVM):[18]

whereηSPDis quantum eきciency of the single-photon detector.

In the event of the “click”,the corresponding state|ψout〉in the signal channel can be expressed as:

Assuming the transmission of the beam-splitter is sufficiently low to ensure that the higher-order terms can be neglected,then the output state in the signal channel can be written as:

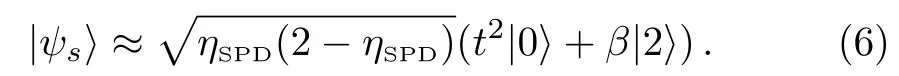
However,in practical implementation,the bi-photon state can not be prepared with 100%eきciency and the vacuum component will also have contribution,i.e.,ρ|2〉=η|2〉|2〉〈2|+(1 −η|2〉)|0〉〈0|,whereη|2〉is the preparation eきciency of state|2〉.Taking the imperfect preparation eきciency into account,the output ensemble will be:

The ensemble in the signal channel can be expressed as:

which can be re-normalized as:

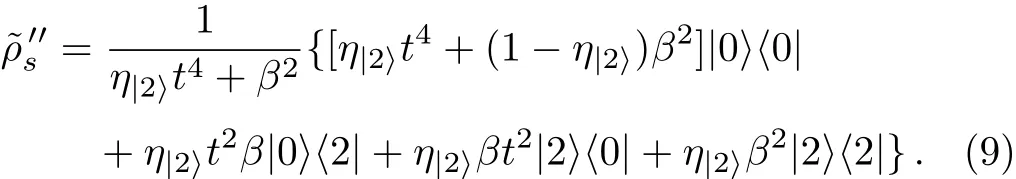
We find from the above that,the detection eきciency of single-photon detectors only contribute an overall factor and have no in fluence on the relative phase or proportion of the final state.While the composition of the initial state(η|2〉)will indeed affect the construction of the final ensemble.

3 Numerical Simulations

In order to evaluate the final generation states,let us investigate the Wigner functions under different experimental conditions.Here,we set a reasonable parameter for the detection eきciency of single-photon detectors,i.e.,ηSPD=0.5.First,assuming the preparation eきciency of the input stateη|2〉is ideal,we do corresponding numerical simulations and plot the Wigner functions with various squeezed parameters,as shown in Figs.2(a)–2(d).

Here Figs.2(a)–2(d)each corresponds to different intensity of the initial two-mode squeezed states,i.e.,β=0,0.005,0.01,0.05,respectively. As expected,Fig.2(a)shows only classical feature,while they perform distinct nonclassical characteristics in Figs.2(c)–2(d).Moreover,from Fig.2(a)to Fig.2(d),it displays a gradual transition from highly classical to highly nonclassical state with the increasing of the squeezed parameterβ,very similar to a“Schrödinger-Cat-like State”.

Then let us consider more realistic conditions,i.e.,the preparation eきciency of the input bi-photon Fock state|2〉is imperfect,corresponding simulation results are shown in Figs.3(a)–3(d).Here the preparation eきciency of the bi-photon state is reasonably set at the value of 80%.Similar to Fig.2,from Figs.3(a)–3(d),they exhibit a gradual transition from highly classical state to highly nonclassical state with the increasing ofβ,but in each case corresponding amplitude of the Wigner function decreases a little bit than in Fig.2.

Furthermore,we calculate the state fidelity of the final state in our scheme by applying the following formula:[20]

whereρsandeach represents the density matrix of the ideal target state and the generation state with our scheme,individually.Corresponding results are shown in Figs.4(a)and 4(b).

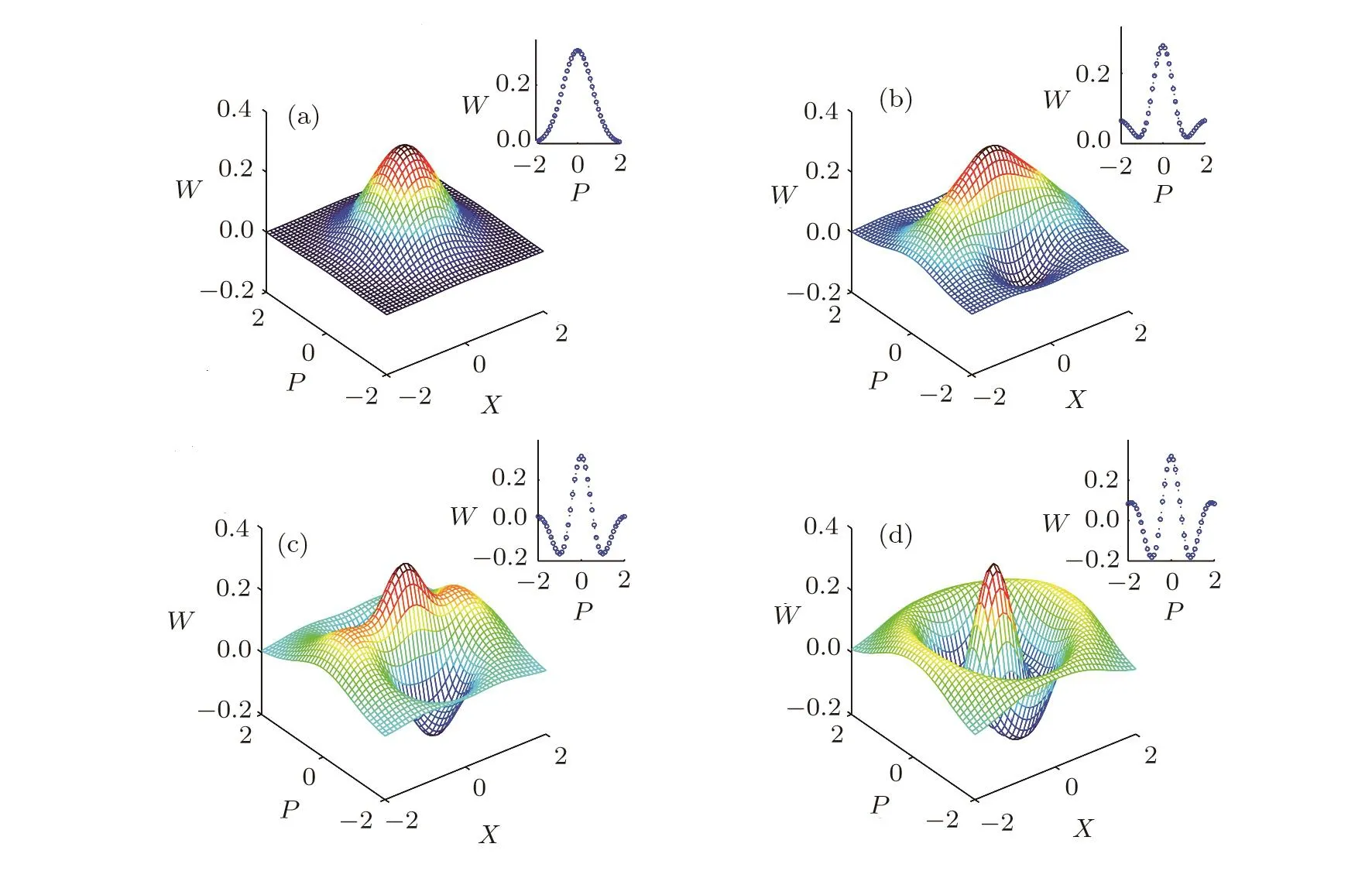
Fig.2 (Color online)Wigner functions of the conditional states under ideal experimental conditions.(a)–(d)The quantum states are calculated with various squeezed parameters:(a)β=0,(b)β=0.005,(c)β=0.01,(d)β=0.05.The inset is the Wigner function in the plane of X=0.

In Fig.4(a),the variation of the state fidelity with the noise(1−η|2〉)in the initial bi-photon state is plotted out for two squeezed parameters,i.e.,β=0.005,0.01,individually.Clearly,the state fidelity decreases with the increasing of noise.Besides,the largerβ,the faster the slope declines.For example,within certain noise(1−η|2〉)≤ 0.2,the state fidelity is always greater than 99%forβ=0.005,while it keeps above 94%forβ=0.01.

Fig.3 (Color online)Wigner functions of the conditional states under imperfect experimental conditions.Here,we set reasonable values for the preparation eきciency of the initial bi-photon state: η|2〉 =0.8,and the detection eきciency of single-photon detector:ηSPD=0.5.The quantum states are calculated with various squeezed parameters:(a)β=0,(b)β=0.005,(c)β=0.01,(d)β=0.05.The inset is the Wigner function in the plane of X=0.

Fig.4 (Color online)(a)The state fidelity versus the noise in the preparation of|2〉(1 − η|2〉)for two different squeezed parameters,β =0.005,β =0.01.(b)The fidelity variation with either the noise(1−η|2〉)or the squeezed parameters β.The horizontal axis represents the noise in the preparation of|2〉(1 − η|2〉)and the vertical axis corresponds to the squeezed parameters(β).The colors denote different values of state fidelity,as scaled in the legend.

Moreover,in order to give a more vivid picture,we also plot out the continuous variation of the state fidelity with both the noise in the preparation of|2〉and the squeezed parametersβ,see Fig.4(b).As expected,the state fidelity gradually declines with the increasing of either the noise in the preparation of|2〉or the squeezed parametersβ.Within practical experimental conditions,e.g.,the noise(1 −η|2〉)is less than 0.2,andβis below 0.05,the state fidelity is always above 80%.

In addition,if the output state becomes mixed state instead of superposition state of|0〉and|2〉due to some experimental operation errors,this can be easily veri fied either by measuring its Winger function or state fidelity.Below we use the typical mixed stateρ=|0〉〈0|+η|2〉|2〉〈2|as an example,and plot out its Winger function and state fidelity,respectively,see Figs.5(a)and 5(b).Obviously,from Fig.5(a)its Winger function does not show any nonclassical characteristic compared with Fig.3(c),and from Fig.5(b)its state fidelity also keeps with much lower value compared with Fig.4(b).

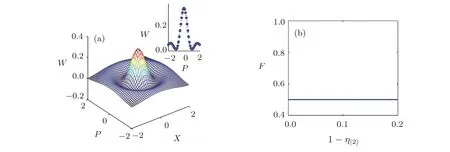
Fig.5 (Color online)(a)The Wigner function for the mixed state=|0〉〈0|+η|2〉|2〉〈2|.(b)Corresponding state fidelity versus noise for the above mixed state.

4 Conclusions

In conclusion,we have presented a new approach on generating any bi-photon superposition state by making use of the entanglement property of the beam-splitter and the post-selection process of threshold single-photon detectors.Furthermore,we do investigation on both the Wigner function and state fidelity of those generation states and carry out corresponding numerical simulations.Our simulation results demonstrate that even with practical experimental conditions,i.e.,non-ideal initial input state or imperfect single-photon detectors,we can still observe a gradual transition from the classical to the nonclassical characteristics,and a quite high state fidelity can be achieved as well.In addition,this scheme needs only linear optics and can be realized with current technology.Therefore,it shows a promising venue in generating nonclassical states in the field of quantum optics.

[1]S.J.Van and O.Hirota,Phys.Rev.A 64(2001)022313.

[2]H.Jeong,M.S.Kim,and J.Lee,Phys.Rev.A 64(2001)052308.

[3]X.Wang,Phys.Rev.A 64(2001)022302.

[4]A.P.Laund,T.C.Ralph,and H.L.Haselgrove,Phys.Rev.Lett.100(2008)030503.

[5]P.Marek and J.Fiurasek,Phys.Rev.A 82(2010)014304.

[6]A.Tipsmark,R.Dong,A.Laghaout,P.Marek,M.Jezek,and U.L.Andersen,Phys.Rev.A 84(2011)050301.

[7]Y.F.Huang,B.H.Liu,L.Peng,Y.H.Li,L.Li,C.F.Li,and G.C.Guo,Nat.Commun.2(2011)546.

[8]X.C.Yao,T.X.Wang,P.Xu,H.Lu,G.S.Pan,X.H.Bao,C.Z.Peng,C.Y.Lu,Y.A.Chen,and J.W.Pan,Nature Photo.6(2012)225

[9]K.Lake,S.Weidt,J.Randall,E.D.Standing,S.C.Webster,and W.K.Hensinger,Phys.Rev.A 91(2015)012319

[10]U.L.Andersen and J.S.N.Nielsen,Phys.Rev.A 88(2013)022337.

[11]A.I.Lvovsky,R.Ghobadi,A.Chandra,A.S.Prasad,and C.Simon,Nature Phys.9(2013)541.

[12]H.Jeong,A.Zavatta,M.Kang,S.W.Lee,L.S.Costanzo,S.Grandi,T.C.Ralph,and M.Bellini,Nature Phys.8(2014)564.

[13]O.Tetsuo,U.Masahito,and I.Nobuyuki,Phys.Rev.A 43(1991)6458.

[14]L.Amine,S.N.N.Jonas,R.Ioannes,K.Christian,T.Anders,and L.A.Ulrik,Phys.Rev.A 87(2013)043826.

[15]M.Dakna,T.Anhut,T.Opatrny,L.Knöll,and D.G.Welsch,Phys.Rev.A 55(1997)3184.

[16]C.W.Lee,J.Lee,H.Nha,and H.Jeong,Phys.Rev.A 85(2012)063815.

[17]Y.Shen,S.M.Assad,N.B.Grosse,X.Y.Li,M.D.Reid,and P.K.Lam,Phys.Rev.Lett.114(2015)100403.

[18]A.I.Lvovsky and J.Mlynek,Phys.Rev.Lett.88(2002)250401.

[19]K.J.Resh,J.S.Lundeen,and A.M.Steinberg,Phys.Rev.Lett.88(2002)113601.

[20]Q.Wang and Y.S.Zhang,Eur.Phys.J.B 85(2012)225.