基于期望语义距离的不确定k近邻分类方法

赵秦怡，黑韶敏

（大理大学数学与计算机学院，云南大理 671003）

分类是数据挖掘一个重要的研究方向，国内外诸多学者进行了大量的研究工作，提出了如决策树分类、贝叶斯分类、基于规则的分类、神经网络分类、支持向量机等各具特色的分类算法，传统的分类算法都是针对确定性数据提出的。在大数据环境下，不确定数据是普遍存在的，如原始数据不准确、使用粗粒度数据集合、处理缺失值、数据集成中引入的不确定性等都会导致数据的不确定。

近年来，不确定性数据在数据挖掘领域的研究得到越来越多的关注，不确定数据分类研究是其中重要的研究分支。BI J B等〔1〕提出了一种面向不确定数据的基于支持向量机分类方法。杨志民等〔2〕利用未确知理论，建立离散型属性不确定性数据模型，将其引入到支持向量机分类模型中。CHENG R等〔3〕提出一种属性级不确定数据的朴素贝叶斯分类方法，方法采用了基于均值和基于分布的类条件概率密度函数。QIN B等〔4〕提出了两种针对区间不确定数据的朴素贝叶斯分类方法，方法基于不确定数据在区间上满足高斯分布的假设，通过不确定数据类条件概率密度函数上的积分预测未知类别样本的类别标签。QIN B等〔5〕提出了一种基于规则的不确定分类方法。QIN B等〔6〕提出了一种不确定决策树分类算法，决策树中不确定数据的属性分裂度量准则是基于概率势的思想。吕艳霞等〔7〕提出了一种大数据环境下的不确定数据流在线分类算法，其决策树的叶子节点利用加权贝叶斯分类算法提高分类准确率，算法可以快速高效地分析不确定数据流。

不确定性数据主要分为元组存在不确定和元组属性值不确定两种类型。本文针对元组属性值不确定提出了一种基于期望语义距离的k近邻（KNN）分类方法，对象的不确定属性值用概率分布向量描述，对象间的距离用期望语义距离计算。

1 相关定义

值不确定性是指一个对象的某个属性可能取这个值，也可能取另一个值。在概率论方法中，对于不确定性连续属性，采用概率密度函数表达数据对象的属性值，而对于不确定性离散属性，可以采用概率分布向量表达数据对象的属性值〔8-10〕。在基于不确定性数据的KNN分类中，需要建立描述对象间期望语义距离关系的数学模型〔11〕。期望语义距离计算模型基于离散型属性，对于连续值属性来说，只需用攀升概念层次树的方法将其离散化〔12〕。

例1对象o1、o2、o3由不确定性离散属性“成绩”描述，“成绩”的值域为{优秀、良好、及格、不及格}，o1的“成绩”属性值的概率分布向量o1.P=（0.9，0.1，0，0），o2.P=（0，0，0.9，0.1），o3.P=（0，0，0.1，0.9）。从语义的角度，可以判断出o2离o1较近。

定义1在概念层次树T中，结点node的深度d（node）是指从根结点到node的路径长度。结点node的高度h（node）是指从node到以node为根结点的子树中的叶结点的最长路径长度。概念层次树T的高度h（T）是指根结点的高度。结点node的层次l（node）定义为l（node）=h（T）-d（node）。

例2 关于气候对象“区域”属性的概念层次树，如图1所示。

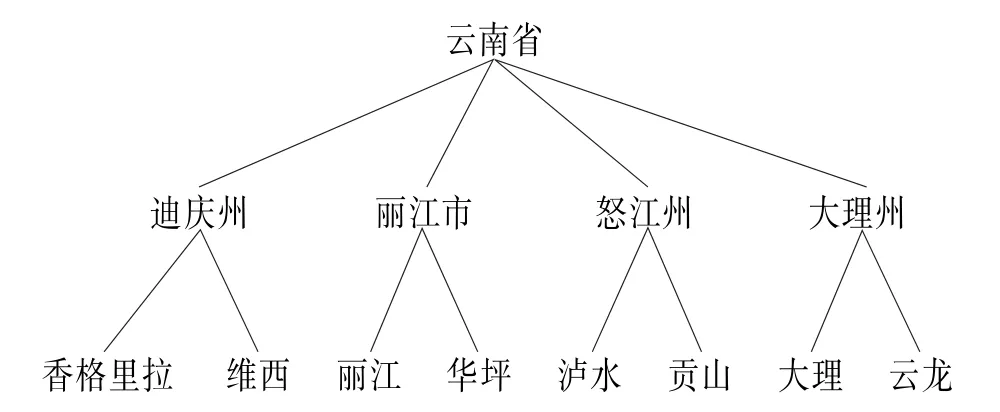
图1 “区域”属性的概念层次树

定义2在概念层次树T中，设结点node1和node2的最近公共祖先是a（node1，node2）。结点node1和node2的语义距离定义为：

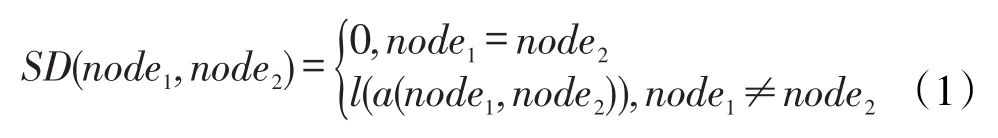
定义3当假设对象独立时，值不确定性离散对象ou和ov的属性值（概率分布向量）ou［Ai］=ou.PAi和ov［Ai］=ov.PAi之间的期望语义距离定义为〔11〕：

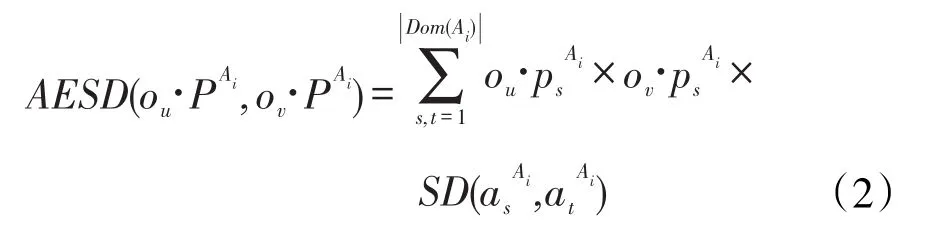
定义4值不确定性离散对象ou和ov之间的期望语义距离定义为〔11〕：

其中，当q=1时，求出的语义距离是曼哈顿距离，当q=2时，求出的语义距离是欧几里得距离，当q＞2时，求出的语义距离是闵可夫斯基距离。在该方法计算语义距离时，设不确定离散属性的值域有n个值，则属性的不确定语义距离最多有n（n-1）∕2个。

定义5设不确定离散属性Ai有nsdAi个不同值的语义距离，这些语义距离从小到大排列为当假设对象独立时，值不确定性离散对象ou和ov的属性值（概率分布向量）o［uA］i=ou.PAi和o［vA］i=ov.PAi之间的期望语义距离定义为〔11〕：

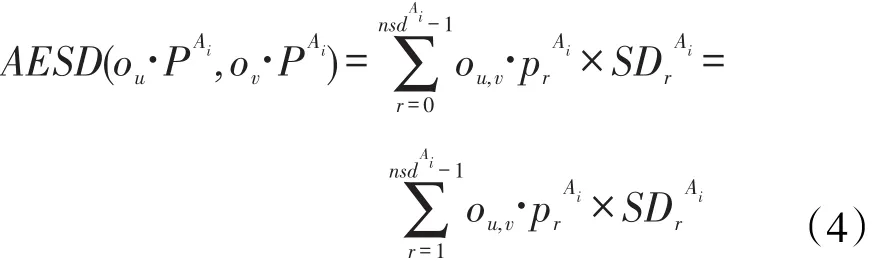
2 基于期望语义距离的不确定k近邻分类法

2.1 算法思想在众多的分类算法中，KNN分类法有难得的优点，如易于编程，不需要优化和训练，在某些问题上具有很高的分类精确度，并且随着设计样本容量的增大估计出的概率偏差会降低等优点〔12〕。KNN分类法的基本形式为：要分类一个输入的新对象y，可在训练数据集合中找出与y距离最近的k个对象，然后把这k个对象中大多数对象所属的类赋给新对象y。

对象间的语义距离反映了对象间的相似性，语义距离越小，对象之间相似度越高，反之亦然。在不确定数据环境下，训练集中对象的属性取值具有不确定性，对于离散型属性可用概率分布向量描述属性的可能取值概率，向量中的分量表示属性取某个值域可能的概率。离散型不确定性属性值间的距离实际上是指两个概率分布向量之间的距离，用传统的距离计算方法不适用，算法中用了期望语义距离计算。由式（1）根据属性的概念层次树计算对象属性值概率分布向量中所有分量间的期望语义距离，由式（2）计算不确定属性间期望语义距离，但此方法计算耗费较大，由式（4）定义可知，根据不同的语义距离值建立属性值分量语义距离索引表，可简化值不确定性属性之间期望语义距离的计算。待分类对象和训练集中对象间期望语义距离的计算由式（3）定义。

例3o1，o2，o3，o44个气候对象的“区域”属性描述，在该属性上的值概率分布如表1所示，“区域”属性的概念层次树见图1。

表1 4种气候在“区域”属性上的概率分布（概率向量）

根据概念层次树，计算“区域”属性值域中的分量之间的语义距离，计算结果见表2。

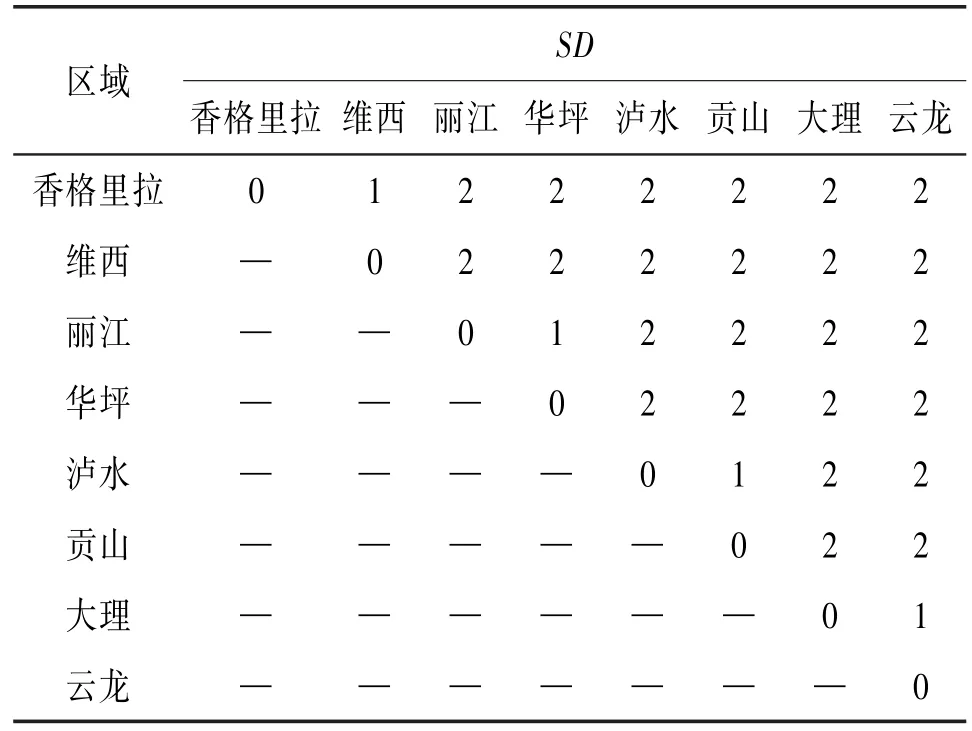
表2 “区域”属性值域中分量之间的语义距离

根据定义5，建立“区域”属性值域语义距离的索引表，见图2。

图2 “区域”属性值概率分布向量语义距离索引表

计算“区域”属性值（概率分布向量）的期望语义距离及o1，o2，o3，o44个气候对象之间的期望语义距离，结果见表3。

表3 4个对象间的期望语义距离

由表3可知，距离o1最近的对象是o3，距离o2最近的对象是o4。

2.2 算法描述

输入：不确定训练数据库T、待分类对象集合O、属性概念层次树、k

输出：待分类对象所属类标签

算法伪代码：

forall attributeAiinN∕∕对训练集中的每一属性

{

compute_elements_SD（Ai）； ∕∕计算属性值概率分布向量中分量值间的语义距离

create_attribute_index（Ai）；∕∕建立属性值概率分布向量语义距离索引表

}

foralloinO∕∕对每一个待分类对象

{ foralltinT∕∕对训练集中的每一对象

{ compute_stribute_instance_distance（o，t）； ∕∕计算属性间的语义距离

compute_expected_instance_distance（o，t）；

∕∕计算对象间的语义距离

sort（distance）；∕∕语义距离排序

min（k，distance）→objects（C）； ∕∕找出前k个语义距离最小的对象

max_class（C）→label； 获得前k个最近邻对象的最大类

}

}

3 算法分析及实验

本算法的时间耗费主要集中在属性间语义距离的计算阶段，设训练集有n个对象，每个对象m个属性，每个属性最多有k个概率分布分量，则算法的时间复杂度为O（nmk2）。由于KNN分类法是基于要求的学习法，当需要与待分类对象比较距离的近邻对象数量很大时，算法可能招致高的计算开销，且当数据中存在大量与分类不相关属性时，分类准确率会产生误差。在数据预处理阶段，对训练集进行属性相关分析，可以去除与分类任务不相关的属性，降低训练集的维度，提高分类的精确度。属性相关分析可采用计算属性信息增益的方法实现〔12〕，信息增益较大的属性与类属性相关较大，计算各属性的不确定因子U（A）。

定义6 属性的不确定U（A）定义如下：

其中Gain（A）为属性A的信息增益，I（s1，s2，…，sm）为待分类对象集的信息熵。由公式可知属性A的不确定因子在0和1之间变化，U（A）为0说明属性A与类属性之间统计无关，U（A）为1说明属性A与类属性之间最大相关。相关分析的目的就在训练数据库中保留前n个相关程度高的属性或不确定因子大于阈值的属性。

本次实验采用合成数据，训练集中含2 000个对象，10个属性，每个属性值概率分布向量含5个分量，期望语义距离计算采用欧氏距离。实验环境：intel core（TM）i7-7500U 的 CPU，2.7 GHz主频，8 GB内存，Windows 10操作系统，编程环境为Vc++6.0，数据库管理系统为SQL Server 2008。

（1）取不同k值时的分类准确率比较，结果见表4。

表4 取不同k值的分类准确率比较

（2）将本算法与文献〔3〕中的属性值不确定贝叶斯分类方法比较，结果见表5。

表5 算法分类准确率比较

实验结果表明，此算法是一个分类准确率好的基于不确定数据分类方法。算法中k的取值对分类结果有一定的影响，但这种影响是无规律的，分类时，k值可由领域专家指定，或通过实验数据给定。

4 结束语

在关系数据库的众多分类算法中，KNN分类法有难得的优点，但如果训练集较大时，算法的时间耗费也增大〔12〕。在本算法中，在期望语义距离计算阶段进行合理剪枝，降低算法的时间耗费，是今后的努力方法。

〔1〕BI J B，ZHANG T.Support Vector Classification with input Data Uncertainty〔J〕.IN Advances in Neural In⁃formation Processing Systems，2005（17）：161-168.

〔2〕杨志民，绍元海，梁静.未知支持向量机〔J〕.自动化学报，2013，6（30）：895-901.

〔3〕CHENG R，REN J，LEE S D，et al.Naïve bayes classi⁃fication ofuncertain data〔C〕∕∕Data Mining，2009，ICDM’09，Ninth IEEE InternationalConferenceon.2009：944-949.

〔4〕 QIN B，XIA Y，WANG S，et al.A novel Bayesian classification foruncertain data〔J〕.Knowledage-Based Systems，2011，24（8）：1151-1158.

〔5〕 QIN B，XIA Y，PRABHAKAR S， et al.A Rule-Based Classification Algorithm for Uncertain Data〔C〕∕∕Data Engineering，ICDE 2009，IEEE International Con⁃ference on.2009：1633-1640.

〔6〕QIN B，XIA Y，LI F.Dtu：A decision tree for uncer⁃tain data〔C〕∕∕In Proceedings of the 13th Pacific-Asia Conference on Knowledge Discovery and Data Mining，PAKDD.2009：4-15.

〔7〕吕艳霞，王翠荣，王聪，等.大数据环境下的不确定数据流在线分类算法〔J〕.东北大学学报（自然科学版），2016，37（9）：1245-1248.

〔8〕高世健，王丽珍，肖清.一种基于U-AHC的不确定空间co-location模式挖掘算法〔J〕.计算机研究与发展，2011，48（S）：60-66 ．

〔9〕陆叶，王丽珍，陈红梅，等.基于可能世界的不确定空间co-location模式挖掘研究〔J〕.计算机研究与发展，2010，47（S）：215-221．

〔10〕肖清，陈红梅，王丽珍.基于DS理论的不确定空间co-location模式挖掘〔J〕.云南大学学报（自然科学版），