求复函数极点、本质奇点的新方法

王凡彬

（1.内江师范学院数学与信息科学学院，四川内江 641110；2.四川省数据恢复重点实验室，四川内江 641110）

众所周知，复变函数f(z)的孤立奇点分为3类：可去奇点，极点，本质奇点。一般来说，可去奇点较易求得。如果z0是f(z)的孤立奇点，而a≠∞，为复常数，则z0就是f(z)的可去奇点。但是极点、本质奇点的求得就较为困难。现行的教材〔1〕也给出了一些方法，但在具体的求解过程中，往往比较麻烦。已有学者对求复函数的极点及其阶数的新方法进行了探讨，得到了相关的一些结果〔2-6〕；而对求复函数的本质奇点新方法的探讨，并不多见，甚至可以说是一个空白。笔者通过研究复函数极点、本质奇点的相关性质，得出了求f(z)的极点及其阶数，求其本质奇点的新方法。这些新方法较之现有的结果，更加方便、快捷。

1 求极点及其阶数的新方法

定理1设f(z)=φ(z)±ψ(z)，并且z=z0(z0≠∞)是φ(z)的m阶极点，而ψ(z)在z=z0解析，则z=z0也是f(z)的m阶极点。

证明：因为z=z0是φ(z)的m阶极点，则

令k(z)=h(z)±(z-z0)mψ(z)，显然k(z)在z=z0解析，且

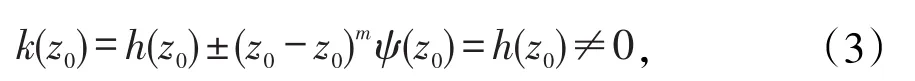
从而z=z0是f(z)的m阶极点。

定 理 2设f(z)=φ(z)ψ(z),

其中h(z)在z=z0解析，且h(z0)≠0。则并且z=z0(z0≠∞)是φ(z)的m阶极点，而ψ(z)在z=z0解析，且ψ(z0)≠0，则z=z0也是f(z),g(z)的m阶极点。

证明：因为z=z0是φ(z)的m阶极点，则

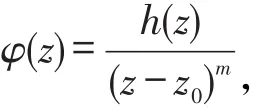
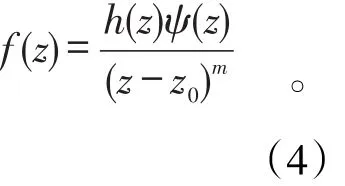
显然，h(z)ψ(z)在z=z0解析，又由ψ(z0)≠0，知h(z0)ψ(z0)≠0,从而z=z0也是f(z)的m阶极点。

其中h(z)在z=z0解析，且h(z0)≠0。则由已知条件知z)在 z=z0解析，且，由前面所证结果知z=z0也是g(z)的m阶极点。

对z0=∞,也有相应的结果。

定理3设 f(z)=φ(z)±ψ(z),并且z0=∞是φ(z)的m阶极点，而ψ(z)在z0=∞解析，即存在，则z0=∞也是f(z)的m阶极点。

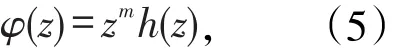
证明：因为z0=∞是φ(z)的m阶极点，则其中h(z)在z0=∞解析，a为有限数，a≠0,那么

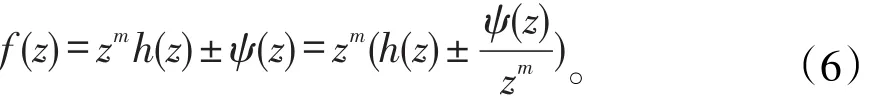
注意

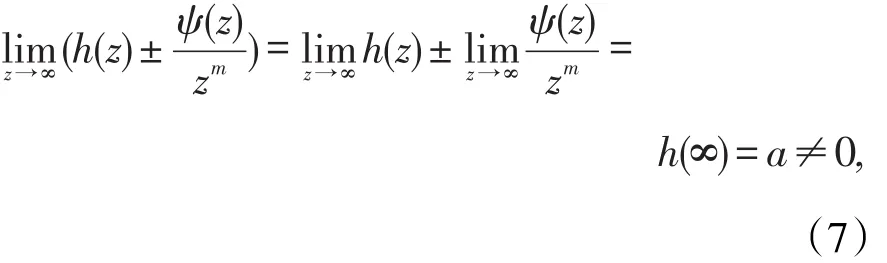
故z0=∞是f(z)的m阶极点。

定理4设并且z0=∞是φ(z)的 m 阶 极 点 ，而 ψ(z)在 z0=∞ 解 析 ，即=ψ(∞)=a存在，且a≠0，则 z0=∞也是 f(z),g(z)的m阶极点。

证明：因为z0=∞是φ(z)的m阶极点，则

其中h(z)在z0=∞解析h(z)=h(∞)=b，b为有限数，b≠0，则

根据条件，可 知 h(z)ψ(z)在 z0=∞ 解析，而，说明 z0=∞ 也是 f(z)的m阶极点。

定理1，定理2，定理3，定理4的优点在于，在满足一定的条件下，我们可以只求出φ(z)的极点及其阶数，就可以求出f(z)的极点及其阶数，简化了工作过程，提高了效率。

2 求本质奇点的新方法

定理5设 f(z)=φ(z)±ψ(z)，并且z=z0(z0≠∞)是φ(z)的本质奇点，而 ψ(z)在 z=z0解析，则 z=z0也是f(z)的本质奇点。

证明：因为z=z0是φ(z)的本质奇点，所以不存在。但ψ(z)在z=z0解析，所以存在。故不存在，这说明 z=z0也是f(z)的本质奇点。

定理6设，并且 z=z0(z0≠∞)是φ(z)的本质奇点，而 ψ(z)在 z=z0解析，且ψ(z0)≠0，则z=z0也是 f(z)，g(z)的本质奇点。

证明：因为z=z0是φ(z)的本质奇点，所以不存在。而ψ(z)在z=z0解析，所以故不存在，所以 z=z0也是 f(z)的本质奇点。

对z0=∞，我们也有如下相应的结果。

定理7设 f(z)=φ(z)±ψ(z)，并且z0=∞是φ(z)的本质奇点，而ψ(z)在z0=∞解析，ψ(∞)≠∞，则z0=∞也是f(z)的本质奇点。

证明：因为z0=∞是φ(z)的本质奇点，所以不存在。而ψ(z)在z0=∞解析，所以存在。故不存在，所以z0=∞也是f(z)的本质奇点。

定理 8设是φ(z)的本质奇点，而ψ(z)在z0=∞解析，且ψ(∞)=a≠0，a为有限数，则z0=∞也是f(z),g(z)的本质奇点。

证明：因为z0=∞是φ(z)的本质奇点，则不存在。而ψ(z)在z0=∞解析，ψ(∞)=a≠0，则也不存在，即z0=∞也是f(z)的本质奇点。

定理5，定理6，定理7，定理8的优点在于，在满足一定的条件下，我们可以只求出φ(z)的本质奇点，就可以求出f(z)的本质奇点。抛掉了ψ(z)，“轻装前进”，提高了工作效率。

3 新方法的应用

对于上述8个定理的优越性，我们通过例题可以看得更清楚。

例 判断下列函数的奇点及其类别（包括无穷远点）。

解：，故z=0为f(z)可去奇点。

对zk=2kπi,k=±1,±2,…,取ψ(z)在zk显然是解析的。

根 据 定 理 1，zk=2kπi，k=±1，±2，…，就 是的一阶极点。

而zk→∞(k→∞)，故∞为非孤立奇点。

对z=0，取ψ(z)=ez。ψ(z)在z=0解析，且ψ(0)=1≠0。

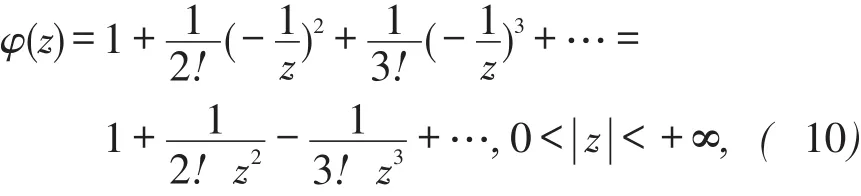
根据定理6，z=0也是的本质奇点。

对z=∞，取ψ(z)在z=∞解析，且ψ(∞)=1。

取φ(z)=ez，

说明z=∞是φ(z)的本质奇点。

按定理8，z=∞是的本质奇点。

（3）对z=0，sinz在z=0解析。而

z=0为的本质奇点。根据定理5，z=0也是f(z)的本质奇点。

故z=∞为sinz的本质奇点。根据定理7，z=∞是f(z)的本质奇点。

上述例题如果不用新方法处理，而按教材的方法做的话，相当繁杂。因此可见，新方法是值得推广的。

〔1〕钟玉泉.复变函数论〔M〕.4版.北京：高等教育出版社，2015.

〔2〕刘国忠.关于极点级数的判定及其留数计算的两个问题〔J〕.北京师范学院学报（自然科学版），1990，11（4）：80-84.

〔3〕王文琦.确定复杂复变函数极点阶数的一种方法〔J〕.山西大同大学学报（自然科学版），2012，28（1）：19-20.

〔4〕申卯兴.一类复变函数极点的判定〔J〕.工科数学，1992，2（8）：97-98.

〔5〕杨艳红.复变函数零点与孤立奇点探析〔J〕.甘肃联合大