空间co-location模式挖掘表实例的计算方法

曾 新，李晓伟，杨 健

（大理大学数学与计算机学院，云南大理 671003）

随着移动技术的快速发展和广泛普及，人们可以利用先进的空间数据收集系统，例如地理信息系统（GIS）、全球位置系统（GPS）等，以至于积累了大量的空间数据集。

面对具有海量性、高维性、非线性、多尺度和模糊性等特点的空间数据集，如何从空间数据库当中挖掘出潜在的、人们感兴趣的知识或其他没有显示在存储空间数据库中的模式，从而指导科学决策，显得尤为重要，目前空间数据挖掘已经成为热点研究内容之一。

空间co-location模式表示空间对象的一个子集，其对象实例经常被发现同时出现在同一邻近区域内，如交通堵塞常常伴有交警、车祸和救护车的出现；在生态学中，尼罗鳄出现的地方也会频繁出现埃及鸻〔1〕。

1 相关工作

自从Agrawal等人研究出Apriori算法以来，colocation模式挖掘成为数据挖掘的研究热点之一，基于确定数据集、不确定数据集和空间数据集的研究成果不断涌现。Join-based算法首次在文献〔1〕中被提出，将频繁模式通过全连接的方式产生候选模式，然后计算所有候选模式的表实例，最后确定其频繁度；针对模式连接操作产生的时间开销问题，文献〔2〕和文献〔3〕分别提出部分连接算法和无连接算法，部分连接算法首先事务化连续的空间数据，并将在事务中未识别的剩余实例采用实例连接的方法，而无连接算法通过星型邻近方式对数据集进行划分，然后采用行实例查找方式来代替时间开销巨大的行实例连接操作；对于不确定数据集，模糊参与率、模糊参与度和模糊对象的co-location模式挖掘算法（FB）在文献〔4〕中被提出；文献〔5〕针对空间对象实例存在约束条件问题，提出带有时间约束的co-location模式挖掘；文献〔6〕针对模式当中存在稀有特征，导致有些模式无法获取的情况，提出一种带稀有特征的空间co-location模式挖掘新方法。

除此之外，文献〔7〕将效用概念引入到空间colocation模式挖掘中，定义了模式效用、模式效用率、扩展模式效用等概念，并提出完全剪枝算法；文献〔8〕针对高平均效用项集挖掘算法需要耗费大量的时间问题，提出将效用信息保存到效用列表当中，并给出高平均效用项集挖掘的改进算法FHAUI；文献〔9〕充分考虑同一特征不同实例间的差异，提出带效用值的空间实例，定义了新的效用参与度UPI作为高效用co-location模式的有趣度量指标，并将领域知识应用到挖掘过程当中；文献〔10〕提出一个高效用项集的增量挖掘算法；目前为止，空间co-location模式挖掘都只关注某一个时刻的空间co-location模式，然而，在实际应用中，数据库中的数据是随着时间变化的，文献〔11〕提出高效的空间co-location模式增量挖掘算法；针对发展的空间数据库当中新的数据和邻近关系，文献〔12〕提出在发展的空间数据库当中有效的更新高效用co-location模式。

2 相关定义及性质

图1中，有A,B,C3个不同空间对象，分别表示不同种类的事务，例如：医院、商店、餐馆，而每个对象出现在不同的位置表示对象实例，对象A,B,C分别有4、2和3个对象实例。

图1 空间对象及其实例

空间邻近关系R用来表示空间对象实例之间的空间关系，一般采用欧几里得距离来表示：

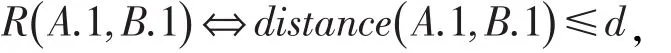
d是预先设定的距离阈值，例如图1中A.1和B.1是邻近的，用实线连接。

假设实例集为I={i1,i2,…,in}，如果I中的任何两个实例间都满足{R(ix,iy)|1≤x≤n,1≤y≤n}则称I为团，例如在图1中{A.1,B.1,C.1}就是一个团。

空间co-location模式表示空间对象的一个子集，用c表示，例如在图1中c={A,B,C}就是一个空间co-location模式。模式c的行实例是一个团，它包含模式c的全部对象，而其任何子集不包含模式c的全部对象。例如在图1中{A.4,B.2,C.2}就是模式c的一个行实例。而模式c的所有行实例组成的集合称为c的表实例，用table_instance(c)来表示。例如在图1中模式c的表实例为：

{{A.1,B.1,C.1},{A.4,B.2,C.2}}。

假设fi为空间的某个对象，fi在模式c={f1,f2,…,fk}中的参与率表示为：

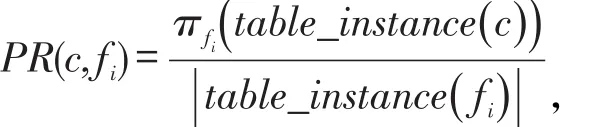
其中π是关系的投影操作，例如在图1中模式c的表实例为{{A.1,B.1,C.1},{A.4,B.2,C.2} }，而对象A,B,C的实例个数分别为4、2和3，模式c中对象参与率为：

模式c的参与度是其所有空间对象参与率的最小值，记为则模式c的参与度为：PI(c)=min(0.5,1,0.67)=0.5。如果模式c的参与度PI(c)大于或等于用户预先设定的最小参与度阈值min_prev，则c是频繁模式，否则c是非频繁模式。例如用户预先设定min_prev=0.5，而PI(c)=0.5≥min_prev，因此模式c是频繁模式。

定理1参与度和参与率随着co-location模式c的阶的增大而单调递减。

证明：假设模式c的行实例中包含某一空间对象fi的实例，如果模式c′是c的子集，那么fi的实例也一定被包含在c′的行实例中，反之则不然，因此空间对象的参与率随着模式阶的增长而递减。

假设c={ }f1,f2,…,fk，

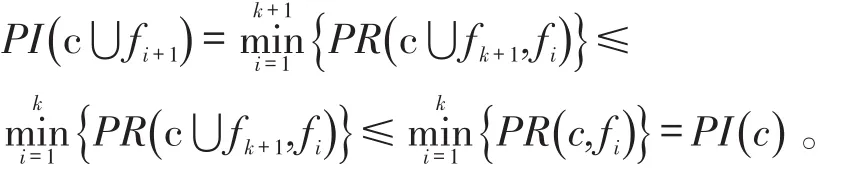
所以模式c的参与度也是单调递减的。

3 算法

3.1 问题描述假设最小参与度阈值min_prev=0.5，图1中模式{A,B}的表实例为{{A.1,B.1},{A.4,B.2}}，{A,C}的表实例为{{A.1,C.1},{A.3,C.3},{A.4,C.2} }，根据参与率和参与度的计算公式有：

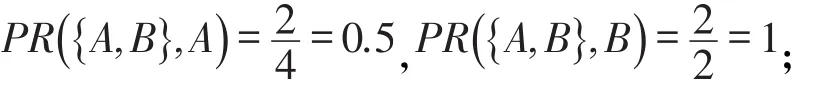
模式{A,B}为频繁模式；

模式{A,C}为频繁模式。同理可知，模式{B,C}也是频繁的。

假定候选模式c={f1,f2,…,fk}，根据co-location模式的反单调性，候选模式c的k-1阶模式都是频繁的，我们称c′={f1,f2,…,fk-1}为模式c的前缀模式，而其他的k-1阶模式均不为前缀模式。例如候选模式{A,B,C}的前缀模式为{A,B}，其他二阶模式不作为其前缀模式。

将频繁模式{A,B}和{A,C}进行连接得到候选模式{A,B,C}，然后，我们通过前缀模式{A,B}的表实例来计算候选模式{A,B,C}的表实例。如果{A,B}的一个行实例{A.i,B.j}中的每个实例都与对象C的一个实例C.m是空间邻近的，那么{A.i,B.j,C.m}为候选模式{A,B,C}的一个行实例，所有行实例的集合为表实例。

例如前缀模式{A,B}的表实例{{A.1,B.1},{A.4,B.2} }，行实例{A.1,B.1}中的每个实例都与对象C的实例C.1空间邻近，所以{A.1,B.1,C.1}为候选模式{A,B,C}的一个行实例，而{A.4,B.2}中每个实例都与C.2空间邻近，{A.4,B.2,C.2}为{A,B,C} 的行实例，最终得出{A,B,C}的表实例为{{A.1,B.1,C.1},{A.4,B.2,C.2}}。

3.2 基本算法在候选模式表实例的计算中，joinbased-D方法与join-based-Z方法的主要区别在于前者将候选模式的前缀模式表实例存储于数据库中，后者将其存放于字典中，但是二者都是基于joinbased算法进行算法设计，具体的算法描述如下：

输入

空间实例集S；

空间邻近距离阈值dis_thre；

最小参与度阈值min_prev;

中间变量

模式的阶k；

k阶co-location模式候选集Ck；

Ck中表实例的集合Tabk；

k阶频繁模式集合Pk；

空间邻近关系集neiR

输出

频繁模式集P

过程：

（1）频繁1项集P1为所有对象；

（2）P=∅；

（3）由实例的坐标和距离阈值dis_thre，产生不同对象实例间的空间邻近关系集neiR；

（4）for( )k=2;Pk-1≠∅;k++

a.将Pk-1连接产生k阶候选模式集Ck；

b.根据Ck、neiR和前缀模式表实例生成候选模式的表实例集Tabk，若通过扫描数据库获取前缀模式作为join-based-D方法，而从字典中获取前缀模式作为join-based-Z方法；

c.根据Tabk计算每个候选模式的参与度；

d.候选模式的参与度大于或等于min_prev，则为频繁模式pk，否则丢弃；

e.P=P⋃Pk；

f.返回频繁模式集P。

4 实验分析

为了评估join-based-D方法和join-based-Z方法在不同的实例集、不同的距离阈值和不同的参与度阈值下的运行效率，本文进行了大量实验，并以对比图的方式呈现实验结果。实验基于的硬件平台为Intel core i3处理器、4 GB内存、64位Win⁃dows 7操作系统；软件编程环境为Python 2.7版本。

4.1 不同实例集下join-based-D与join-based-Z的效率数据集共有10个对象，每个对象的实例个数都是随机生成的，其中邻近距离阈值dis_thre＝5，最小参与度阈值min_prev=0.5，分别在实例个数为152、390、623、940和1 306下比较join-based-D方法和join-based-Z方法的运行效率，见图2。

图2 不同实例集下运行效率

从图2中可以看出，在其他条件一定的情况下，随着实例数目的增大，join-based-Z方法的运行效率要远高于join-based-D方法，但是join-based-Z方法中采用字典存储前缀模式，字典的大小受到内存大小的限制，实例个数达到一定数目时，joinbased-Z方法将无法计算模式的表实例，所以小数据集下采用join-based-Z方法，运行效率高。

4.2 不同距离阈值下join-based-D与join-based-Z的效率数据集共有10个对象，每个对象的实例个数都是随机产生的，在实例数目为623、最小参与度阈值min_prev=0.5的情况下，分别对距离阈值为1、2、3、4和5进行实验，比较join-based-D方法与join-based-Z方法的运行效率，见图3。

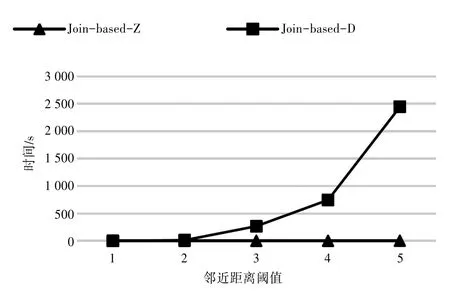
图3 不同邻近距离阈值下运行效率

同一实例集下，随着邻近距离阈值的增大，邻近关系集会随之扩大，候选模式的行实例数目可能会增大，导致表实例的计算开销增加。join-based-D方法多次扫描数据库带来极大的时间开销，而joinbased-Z方法运行效率高。

4.3 join-based-D与join-based-Z在不同参与度阈值下的效率在10个空间对象下，共随机生成623个实例，最小距离阈值dis_thre＝3，分别在参与度阈值为0.5、0.6、0.7、0.8和0.9下进行实验，比较joinbased-D方法和join-based-Z方法在不同参与度阈值下的运行效率，见图4。

图4 不同参与度阈值下运行效率

由于join-based算法的主要时间开销为连接操作和表实例的计算，而参与度阈值用来衡量模式是否频繁的标准。随着参与度阈值的增大，频繁模式的数目会相应减少，导致连接操作和表实例的计算开销适当减少。但是，join-based-Z方法的运行效率仍然高于join-based-D方法。

5 结束语

空间co-location模式挖掘中，模式表实例的计算尤为重要，join-based-D和join-based-Z方法能够实现对候选模式表实例的计算。但是，在内存大小允许的情况下，join-based-Z方法的执行效率要远高于join-based-D方法。由于join-based-Z方法受到内存大小的限制，所以，未来我们将主要研究join-based-Z方法的优化策略。

〔1〕 HUANG Y，SHEKHAR S，XIONG H.Discovering colocation patterns From spatial data sets：a general ap⁃proach〔J〕.IEEE Transactions on Knowledge and Data Engineering， 2004，16（12）：1472-1485.

〔2〕 YOO J S，SHEKHAR S.A partial Join Approach for Mining Co-location Patterns〔C〕∕∕Proc.of the 12th An⁃nualACM Int.Workshop on Geographic Information Systems.Washington DC.USA，2004：241-249.

〔3〕YOO J S，SHEKHAR S，CELIK M.A join-less ap⁃proach for co-location pattern mining：A summary of results〔C〕∕∕In： Proc.of the 5th IEEE Int.Conf.on Data Mining.Washington：IEEE ComputerSociety，2005：813-816.

〔4〕欧阳志平，王丽珍，陈红梅.模糊对象的空间co-location模式挖掘研究〔J〕.计算机学报，2011，34（10）：1947-1955.

〔5〕 ZENG X，YANG J.Co-location patterns mining with time constraint〔J〕.Computer Science，2016，2（43）：293-296.

〔6〕冯岭，王丽珍，高世健.一种带稀有特征的空间co-loca⁃tion模式挖掘新方法〔J〕.南京大学学报（自然科学），2012，48（1）：99-107.

〔7〕杨世晟，王丽珍，芦俊丽，等.空间高效用co-location模式挖掘技术初探〔J〕.小型微型计算机系统，2014，35（10）：2302-2307.

〔8〕王敬华，罗相洲，吴倩.基于效用表的快速高平均效用挖掘算法〔J〕.计算机应用，2016，36（11）：3062-3066.

〔9〕江万国，王丽珍，方圆，等.领域驱动的高效用co-loca⁃tion模式挖掘方法〔J〕.计算机应用，2017，37（2）：322-328.

〔10〕LIN C W，LAN G C，HONG T P.An incremental⁃mining algorithm for high utility itemsets〔J〕.Expert Systems with Applications，2012，39：7173-7180.

〔11〕芦俊丽，王丽珍，肖清，等.空间co-location模式增量挖掘及演化分析〔J〕.软件学报，2014，25（2）：189-200.

〔12〕WANG X X，WANG L Z，LU J，et al.Effectively Updating High Utility Co-location Patterns in Evolv⁃ing Spatial Databases〔C〕∕∕InternationalConference on Web-Age Information Management.Springer Inter⁃