LAT模型频谱感知机制的性能优势研究

俞启明，金 虎，刘轶凡，郑文庆

(国防科技大学电子对抗学院, 安徽 合肥 230037)

0 引言

传统的认知无线电在进行频谱感知时，需要将时隙划分为感知时隙和发送时隙，只有当次用户在感知时隙判决确定没有主用户时，才在发送时隙进行数据传输，这样的模型称为LBT(Listen-Before-Talk)模型。由于主用户的出现是随机的，LBT模型并不能很好地避免数据冲突，其感知时隙的划分也造成了一定的资源浪费。

2011年有学者提出全双工认知无线电的概念[1]，同时同频全双工技术使得在同一时刻同一频率的双向通信成为现实[2-4]，能够将频谱利用率近乎翻倍，两项技术的结合使得认知无线电的频谱利用效率进一步提升。2015年Liao等人对全双工认知无线电进行了系统的阐述，使其具备了完善的理论与应用前景[5]。目前被广泛认可的全双工认知无线电模型是LAT(Listen-And-Talk)模型，即次用户具备同时传输和感知的能力。LAT模型同样会因为主用户出现的随机性，而不可避免地造成数据冲突和一定程度的资源浪费。

由于认知无线电中主次用户的非协作本质，造成了无论是何种感知机制，都会带来不可避免的数据冲突可能和资源浪费可能。本文对比了LAT模型与LBT模型在感知机制上的性能优劣，即比较二者在数据冲突和频谱资源浪费上的差异。通过建立风险函数的方法，证明了LAT模型会带来更少的数据冲突和资源浪费。其相对于LBT模型的优势也说明了研究LAT模型的必要性。

1 LAT模型和LBT模型

全双工认知无线电网络由一个主用户(PU-Primary User)、多个次用户(SUs-Secondary Users)组成，每个次用户配置有两根天线，分别用作数据的收发，次用户均具备自干扰消除的能力。在某一频段上，主用户随机出现。主用户工作时，所有次用户利用接收天线进行频谱感知。主用户退出该频段后，多个次用户竞争出一个工作次用户(假设为SU1)。工作次用户SU1通过发射天线传输数据，同时利用接收天线对该频段进行实时感知，并利用自干扰消除技术，实时地将接收信号中的自干扰排除。一旦判断主用户出现，SU1立即停止数据发送。

传统半双工认知无线电LBT模型的统计判决模型为二元判决，如公式(1)所示：

(1)

式中，r表示感知次用户接收信号，p表示主用户信号，n表示高斯白噪声。H0表示没有主用户出现；H1表示主用户占用频段。

而LAT模型中，受自干扰的影响，感知次用户的检测模型为四元判决问题，如公式(2)所示：

(2)

式中，H00表示PU和SU1同时不占用频段；H01表示仅有PU占用频段；H10表示SU1占用频段而PU不占用频段；H11表示PU和SU1同时占用该频段；s表示工作次用户SU1发出的信号；γ为自干扰消除系数，表示SU1通过射频域、模拟域、数字域联合消除自干扰可以达到的程度[6]。

2 频谱感知风险函数

通过建立风险函数比较LAT与LBT的感知策略：风险函数由两部分组成，即数据冲突带来的干扰和信道空闲带来的浪费，以两部分风险之和更小为标准，判定该型认知无线电的感知机制优越与否。

设：空闲成本为Cw，冲突成本为Cc，且Cc/Cw=k，k≥1，即认知无线电中，主次用户的数据冲突是更恶劣的因素。

考虑到感知机制的比较不涉及具体认知无线电的类型以及频谱感知的方法，所以做如下基本假设：

1)LAT与LBT模型需要的感知时长相同。并且在感知时段内，次用户即可以做出判决。

2)设每个时隙长度为T，时隙被分为感知时隙Ts和数据传输时隙TT。其中Ts=qT,q∈0,1，q表示感知时隙占总时隙的比，次用户在Ts进行感知，当判决没有主用户信号时，在TT时段进行数据传输。

3)检测过程中没有误检测发生。

2.1 LBT模型的风险函数

假设主用户出现的时间段为μ～η，由于主用户的随机性，不妨假设μ和η均服从均匀分布，表示为μ～U0,T，η～UξT,ξT+T，ξ=1,2,…，ξ为主用户信号持续时隙的个数。

LBT模型中，主用户出现的情况如图1所示，四种情况(C1～C4)分别为：

C1：μ∈0,Ts且η∈ξT,ξT+Ts

C2：μ∈0,Ts且η∈ξT+Ts,ξT+T

C3：μ∈Ts,T且η∈ξT,ξT+Ts

C4：μ∈Ts,T且η∈ξT+Ts,ξT+T

四种情况下风险函数不同。以C3为例：当μ∈Ts,T时，次用户在0,Ts时段感知无主用户出现，决定在Ts,T时段进行数据传输，此时造成了时长为Ts的频谱资源浪费，和时长为T-μ的数据冲突。所以此时风险Rμ,TT为：

Rμ,TT=CcT-μ+CwTs

(3)

当η∈ξT,ξT+Ts时，次用户正确感知到主用户的存在，并决定不使用该频段的后续时段，此时不造成数据冲突，但是会造成T-η的资源浪费，所以此时风险Rη,Ts为：

Rη,Ts=CwT-η

(4)

同理，可得：

当μ∈0,Ts时，

Rμ,Ts=Cwμ

(5)

当η∈ξT+Ts,ξT+T时，

Rη,TT=CwT-η

(6)

综合以上四种情况，LBT模型的风险函数可以统一表示为：

RLBT=P(μ∈TS)Rμ,TS+P(μ∈TT)Rμ,TT+

P(η∈TS)Rη,TS+P(η∈TT)Rη,TT

(7)

由于风险函数RLBT是随机变量μ和η的函数，且μ和η均服从均匀分布,而冲突成本和资源浪费成本成倍数关系Cc/Cw=k，k≥1，在此不妨假设Cw=1，则Cc=k。对RLBT求数学期望ERLBT，得：

ERLBT=P(μ∈Ts)ERμ,Ts+

P(μ∈TT)ERμ,TT+

P(η∈Ts)ERη,Ts+P(η∈TT)ERη,TT

=T/2 + (T-Ts)Ts/T+kT-Ts-

=T/2 +k+ 2Ts+kTT-Ts/(2T)

(8)

2.2 LAT模型的风险函数

在LAT模型中，感知时隙始终为Ts。所以只有一种情况，如图2所示：当主用户出现在某个Ts中的μ点时，次用户此时会造成Ts-μ时间的冲突。当主用户在另一个Ts中的η点退出频段后，次用户此时造成2Ts-η时长的浪费。所以LAT模型下的风险函数及其均值如公式(9)、(10)所示：

RLAT=P(μ∈Ts)Rμ,Ts+P(η∈Ts)Rη,Ts

=Cw2Ts-η+Ccμ

(9)

ERLAT=Cw2Ts-Eη+CcEμ

=2Ts-Ts/2+kTs/2

=(3+k)Ts/2

(10)

3 频谱感知性能数值分析

比较两种模型风险的数学期望，显然，当ERLAT≤ERLBT时，全双工认知无线电的性能更好。现令方程Fk=ERLBT-ERLAT，研究方程Fk≥0成立的条件，则该条件等价于LAT模型，优于LBT模型。

由公式(8)、(10)可得：

Fk=T/2+k+2Ts+kTT-Ts/(2T)-

(3+k)Ts/2

(11)

将Ts=qT，q∈0,1代入公式(11)，并进一步化简可得：

Fk,q=k+1-q2-q+1≥0

(12)

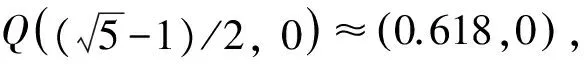
通过分析知道，q∈0,0.618时，LAT性能好于LBT性能，而该条件在当前的认知无线电系统显然是满足的。目前在各型认知无线电中虽然没有对感知时隙有着固定的划分，但是通常而言，感知时隙划分得越长，认知无线电的效率越低。根据文献[7]，感知时隙一般为整个时隙的1/10，并且一般不会超过整个时隙的1/5，即通常Ts=0.1T～0.2T，远不会超过0.618T。可见，LAT的优越性能可以在现实情况下得到保障。

4 结束语

本文通过建立风险函数，从感知机制上证明了LAT模型相对于LBT模型产生数据冲突和资源浪费的可能性更小，从理论上证实了LAT模型具有更高的频谱利用效率。然而，本文在假设中忽略了感知方法造成误检测的可能性，从现有的文献来看，LAT模型造成误检测的可能性高于LBT模型。如何降低LAT模型的误检测性能是未来研究的重点。■

[1] Cheng W, Zhang X, Zhang H. Imperfect full duplex spectrum sensing in cognitive radio networks[C]∥ACM Workshop on Cognitive Radio Networks. ACM, 2011:1029-1034.

[2] Choi JI, Jain M, Srinivasan K, et al. Achieving single channel, full duplex wireless communication.[C]∥ International Conference on Mobile Computing and Networking, MOBICOM 2010, Chicago, Illinois, USA, 2010:1-12.

[3] Everett E, Sahai A, Sabharwal A. Passive self-interference suppression for full-duplex infrastructure nodes[J]. IEEE Trans. on Wireless Communications, 2013, 13(2):680-694.

[4] Duarte M, Sabharwal A. Full-duplex wireless communications using off-the-shelf radios: feasibility and first results[C]∥Signals, Systems and Computers. IEEE, 2010:1558-1562.

[5] Liao Y, Song L, Han Z, et al. Full duplex cognitive radio: a new design paradigm for enhancing spectrum usage[J]. IEEE Communications Magazine, 2015, 53(5):138-145.

[6] 唐友喜. 同时同频全双工原理与应用[M].北京： 科学出版社, 2016.

[7] Robert CQ. 认知无线电通信与组网:原理与应用[M]. 北京：机械工业出版社, 2013.