基于压缩感知的单通道多频带信号感知技术

杨树树， 宁 勇， 董宁斐

(1.中国航天科工集团8511研究所，江苏 南京 210007；2.南京理工大学电子工程与光电技术学院，江苏 南京 210094)

0 引言

传统的数字信号处理是以奈奎斯特(Nyquist)采样定理为基础的，在该框架下，数字系统采样速率必须达到模拟信号带宽的2倍才能无失真地恢复原始模拟信号[1]。然而，随着信息需求量的日益增加，信号带宽越来越宽，信息获取对采样速率和处理速度提出了越来越高的要求，人们迫切需要去寻求新的数据采集和处理的方法。在这种情况下，针对具有稀疏特性信号的采样和处理技术的压缩感知(CS)[2-3]理论应运而生。

目前压缩采样系统主要有基于多陪集(MC)[4]的方法、基于调制宽带转换器(MWC)[5-7]的方法等，这些方法均采用多通道结构，在频率支集未知的情况下能够显著降低采样频率，但是此系统硬件复杂，对通道间的幅相一致性要求较高，系统的稳健性差。本文提出了一种基于周期非均匀采样的多频带信号感知技术，它是一种基于单通道结构的压缩采样系统[8]，重点解决了上述方法实现时硬件复杂度高、设备要求高的问题。

1 周期非均匀压缩采样系统

1.1 理论采样过程

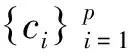
yi[n]=x(nLTnyq+ciTnyq),1≤i≤p

(1)

以上周期非均匀采样过程可用图1表示。

由图1可知，周期非均匀采样系统可由p个起始点不同的采样频率为fnyq/L的A/D转换器实现，图2为周期非均匀采样时序。

1.2 实际采样模式

实际应用过程中，为了避免各通道的不一致性，图1所描述的多通道采样系统可通过一个由非均匀时钟控制的A/D转换器实现，则该采样系统变为一个单通道采样系统，如图3所示。

图3中的非均匀脉冲信号p(t)为周期性的，周期为LTnyq，每个周期内包含p个脉冲，即进行p次采样。一个周期非均匀脉冲信号在一个周期内的波形如图4所示。

图4中脉冲信号的每个上升沿控制A/D转换器的一次采样，各上升沿对应的时间点应该分别为c1Tnyq,c2Tnyq,…,cpTnyq。

2 信号重构

完成对信号的周期非均匀采样后，需要对数据进行信号重构，恢复出原始信号的奈奎斯特采样序列。

2.1 信号加窗

周期非均匀采样系统可以采样得到任意长度的样本序列，但重构算法在一段时间内只能处理有限长的序列，因此，可以利用窗函数对采样序列进行分段[9]。适当的加窗处理可以有效地防止边缘效应，并且可以避免频谱泄露破坏信号频域的稀疏性。为了完全重构出原信号，首先利用分析窗将接收到的无限长序列分段，经过信号处理过程后，再通过综合窗将各段信号拼接起来，恢复出原来的无限长信号。

为了描述整个分段加窗的处理过程，用y′表示周期非均匀采样系统的采样输出序列，用x表示序列y′所对应的原始信号的奈奎斯特采样序列。首先将序列y′插零，将相对于奈奎斯特率采样而言的周期非均匀采样未采到的位置均补零，得到奈奎斯特速率的序列y。将序列y分段，各段长度为N(N/L为偶数)，重叠率为50%，并将各段序列与分析窗函数w1相乘，则得到的第j(j=0,1,…)段序列为：

yj(i)=w1(i)y(i+jN/2),i=0,1,…,N-1

(2)

由于加窗后yj中补零的位置依然为0，因此实际处理过程中无需对序列y′插零。直接将y′按长度M=pN/L进行重叠率为50%的分段，并将分段后序列中的各元素分别与w1中对应位置的窗函数元素相乘，可得到序列yj，则yj中的元素为序列yj中所有的非补零位置的元素。因此，yj可以理解为对分段加窗信号xj(i)=w1(i)x(i+jN/2)进行周期非均匀采样的结果。

分析可知，除去最初的N/2个样本点和最后的N/2个样本点，x(k)中的其他样本点都被映射到xj中的两个位置：第「|2k/N⎤-1段序列的第kmod(N/2)+N/2个点，第「|2k/N⎤段序列的第kmod(N/2)个点。

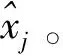
(3)

式中，i∈0,1,…,N-1，j为整数。由式(3)可知，为保证信号的完全重构，窗函数w1、w2需满足：

w1(i)w2(i)+w1(i+N/2)w2(i+N/2)=1

(4)

式中，i=0,1,…,N/2-1。

2.2 重构过程

将周期非均匀采样系统的输出序列y′[n]分为p组新序列yi[n]=y′[np+i-1]，其中1≤i≤p，n=0,1,2,…，则yi[n]=x(nLTnyq+ciTnyq)，其速率为fp=fnyq/L。序列yi[n]的离散时间傅里叶变换可表示为：

exp(j2πfciTnyq),f∈Fp

(5)

式中，Tp=1/fp，Fp=-fp/2,fp/2。

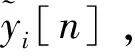
(6)

将式(6)表示为矩阵形式，可得：

(7)

Aik=1/Lexp(j2πci(k-1-L/2)/L)

(8)

向量z(f)是L×1维未知向量，其第i个元素为：

zi(f)=X(f+(i-L/2-1)fp)

(9)

将式(7)转换为时域形式，有：

(10)

频带个数为N的多频带信号所对应向量z(f)的联合稀疏度K满足K≤2N。向量z(f)的联合支撑集S=suppz(f)可以利用一种连续-有限(CTF)模块进行估计，其框架如图5所示。

令：

(11)

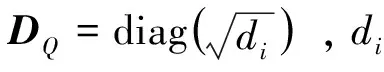
用CTF模块估计出支撑S后，可求出：

(12)

zi[n]=0,i∉S

(13)

(14)

3 仿真实验

3.1 系统重构成功率

设计一个多频带信号周期非均匀采样系统，参数设计为：L=256，p=32。ci在[0,L-1]中随机选取，实验过程中，假设A/D转换器的实际有效位数为13位。

选用由三个符号速率为fd=100 kHz的QPSK信号组成的多频带信号进行实验，分析输入信号的信噪比对系统重构成功率的影响。

由图6可知，对于输入信号的能量系数为Ei=1,10,106的情况，最小信号与白噪声之间信噪比为5dB时，最小信号的重构成功率已达到90%以上。而对于输入信号的能量系数为Ei=1,10,107的情况，即使输入信噪比增高，系统重构成功率也保持在93.5%左右不再提高，这是由有效数字为13位的A/D转换器引起的量化噪声导致的。

3.2 系统重构精度仿真

选用由正弦信号，符号速率均为fd=200 kHz的QPSK信号和BPSK信号三个子信号组成的多频带信号进行实验，分析输入信号的信噪比与重构信号精度的关系。

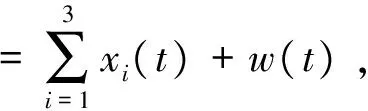
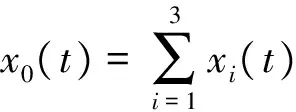
(15)

3.3 压缩比对系统性能的影响

定义周期非均匀采样系统压缩采样的压缩比为β=L/p，因此参数L=256保持不变，通过改变参数p改变系统的压缩比β。

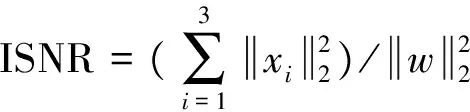
4 结束语

本文介绍了周期非均匀压缩采样工作原理，提出了一种基于单通道结构的压缩采样系统，对该系统进行了仿真实验以及性能分析，相对于传统的多通道压缩采样系统而言，该系统能克服传统多通道压缩采样系统硬件复杂度高、设备要求高的问题，易于工程实现。■

[1] 杨真真，杨震，孙林慧．信号压缩重构的正交匹配追踪类算法综述[J]．信号处理，2013，29(4)：486-496．

[2] Donoho DL，Tsaig Y．Extensions of compressed sensing[J]．Signal Processing，2006，86(3)：533-548．

[3] Candes EJ，Wakin MB．An introduction to compressive sampling[J]．IEEE Signal Processing Magazine，2008，25(2)：2l-30．

[4] Herley C, Wong PW. Minimum rate sampling and reconstruction of signals with arbitrary frequency support[J]. IEEE Trans. on Information Theory，1999，45(5)：1555-1564．

[5] Mishali M，Eldar YC．From theory to practice：sub-Nyquist sampling of sparse wideband analog signals[J]．IEEE Journal of Selected Topics in Signal Processing，2010,4(2)：375-391．

[6] Mishali M，Eldar YC．Xampling：analog to digital at sub-Nyquist rates[J]．Circuits Devices & Systems，IET，2011，5(1)：8-20．

[7] Mishali M，Eldar YC．Wideband spectrum sensing at sub-Nyquist rates[J]．Signal Processing Magazine，2011，28(4)：102-135．

[8] Grigoryan R, Jensen T, Arildsen T, et al. Reducing the computational complexity of reconstruction in compressed sensing nonuniform sampling[C]∥Proceedings of European Signal Processing Conference (EUSIPCO)，2013: 1-5．

[9] Wakin M, Becker S, Nakamura E, et al. A nonuniform sampler for wideband spectrally-sparse environments[J]. IEEE J. Emerg. Sel. Topics Circuits Syst.，2012, 2(3): 516-529．

[10] Grigoryan R, Arildsen T, et al. Performance comparison of reconstruction algorithms in discrete blind multi-coset sampling [C]∥Proceedings of IEEE Int. Sym. Signal Processing, Information Technology (ISSPIT)，2012: 147-152．

[11] Becker SR, Candes EJ, Grant MC. Templates for convex cone problems with applications to sparse signal recovery[J]. Math. Program. Comput.，2011, 3(3): 165-218．

[12] Lee K, Bresler Y. Subspace-augmented music for joint sparse recovery with any rank[C]∥Proceedings of IEEE Sensor Array and Multichannel Signal Processing Workshop (SAM)， 2010: 205-208．