幅相误差对多发多收模式SAR成像影响分析∗

李舆坤,洪 峻,明 峰

(1.中国科学院电子学研究所,北京100190;2.微波成像技术国家重点实验室,北京100190;3.中国科学院大学,北京100049)

0 引言

传统星载单通道合成孔径雷达(SAR)存在最小天线面积限制,宽距离测绘带和高方位分辨率是一对难以调和的矛盾量。星载多通道SAR系统采用数字波束形成技术(Digital Beamforming,DBF)可以有效地突破此限制[1],实现高分辨率宽测绘带对地观测。目前,HRWS SAR系统的主要实现体制有单星方位多通道SAR(Multi-Channel SAR,MC-SAR)系统[2]和分布式小卫星SAR系统[3]等。其中MC-SAR系统又可分为单相位中心多波束SAR(Single Phase Center Multiple-Beam SAR)和偏置相位中心多波束SAR(Displaced Phase Center Multiple-Beam SAR)[4]。偏置相位中心多波束SAR较为常用,其具有两种工作模式:单发多收模式和多发多收模式。单发多收模式下只有一个天线发射信号,所有天线接收信号;而多发多收模式下所有天线均可发射、接收信号。方位多通道SAR在实现高分辨率、宽测绘带的过程中,需要对信号进行DBF解模糊,这就要求各通道的特性一致,通道位置也必须精确已知[5]。然而,对于实际星载SAR系统,各接收通道的幅相特性不可能完全一致,并且各通道天线相位中心位置测量也存在误差,这两类非理想因素造成了通道间幅相不一致,将影响星载MC-SAR系统DBF解模糊性能,对成像造成严重影响。

文献[6]阐述了各通道幅相特性不一致对系统产生的影响,但未考虑天线相位中心误差。文献[7]对星载MC-SAR系统的误差源进行了分析,阐述了各种误差导致的不同影响,并以此对误差源进行了分类,但只对误差影响进行了文字概述,没有通过建立误差模型来定量地分析误差影响。文献[8]通过建立误差模型,分析了天线相位中心误差对导向矢量的影响,但未通过仿真分析该误差对系统成像性能的影响。文献[4]通过数学模型和仿真定量地分析了在单发多收模式下,通道幅相特性误差对系统成像性能的影响,并未考虑到多发多收模式下的情况,也未对各通道天线相位中心误差的影响进行分析。基于此,本文将针对多发多收模式,系统地分析通道幅相特性误差和天线相位中心误差对星载MC-SAR成像性能的影响。

1 方位多通道SAR多发多收模式的基本原理及回波模型

如图1所示,设系统有3个天线,沿方位向排列。3个天线的发射机同时发射相同的信号,由地面点目标反射后3个天线的接收机分别接收。

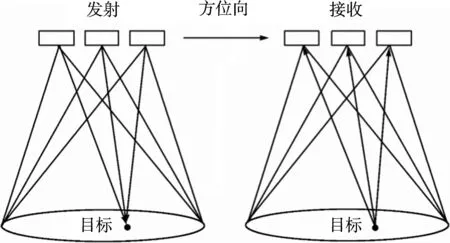
图1 多发多收模式工作原理示意图

因此,每个天线将接收到3个不同的回波,其中,一个回波的信号是该天线自身发射产生的,另外两个回波是其余两个发射机发射产生的,即每个天线接收一个自发自收的信号和两个收发

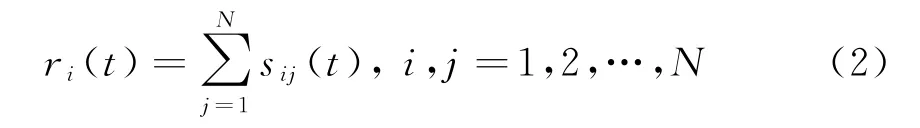
为了进行自发自收等效采样,需要将每个通道接收的不同回波进行分离。文献[11]提出了两种将各回波相互分离的方法。分离后,进而可将该系统3个通道接收的回波等效为单通道在一个PRT内的5次采样得到的回波,具体说明如下。设5个等效采样点分别为a,b,c,d,e,等效单通道在这5个位置得到的回波为s1,s2,s3,s4,s5。由文献[9],等效过程中补偿的常数相位为分置的信号。由文献[9],收发分置得到的回波经补偿一个固定的常数相位后,可等效为一个虚拟天线在接收天线和发射天线相位中心连线的中点处自发自收得到的回波。因此,在多发多收模式下得到的回波数据也可等效为单波束SAR在多个点的采样结果。文献[10]对该等效原理进行了详细说明。

如图1所示,假设各天线同时发射信号,经点目标反射后得到回波。r i(t)表示第i个子天线接收的回波信号;s ij(t)表示由第j个天线发射、第i个天线接收的回波信号。由系统原理可知:其中,d z表示发射天线和接收天线相位中心的间隔距离,R0为天线到点目标的最短斜距,λ为发射信号的波长。在多发多收模式下,三通道的系统存在两种不同的收发天线间隔距离,因此存在两种不同的补偿相位,分别为由此也可得到,由接收天线序号数i和发射天线序号数j所决定的补偿相位的通式:

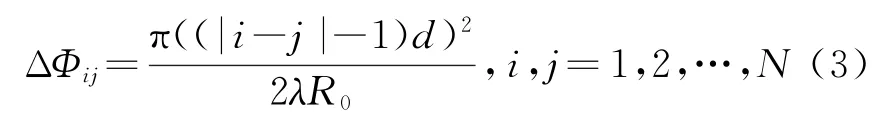
因此,一个PRT内,等效单通道在各方位位置处得到的回波信号为

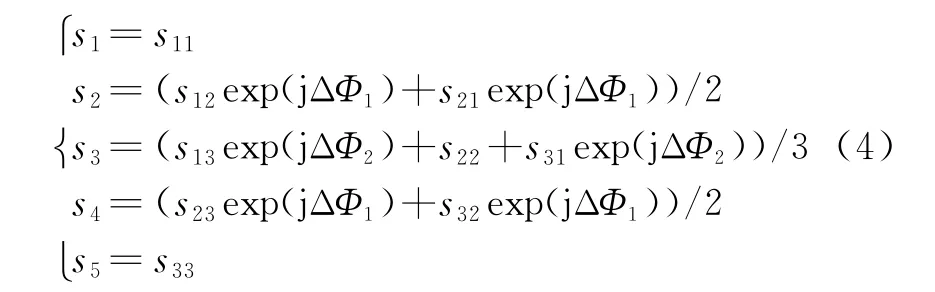
将每个PRT内得到的5个回波依次在方位向排列,即可等效为单波束SAR系统在观测时间内连续采样的结果。为方便以后的分析,将s1,s2,s3,s4,s5和s ij的定义进行拓展,将s1,s2,s3,s4,s5看作沿方位向排列的5个自发自收的虚拟天线分别在观测时间内连续采样得到的回波,其中某一虚拟天线的回波用s m表示,m=1,2,3,4,5;设s ij为由第j个天线发射、第i个天线接收后补偿了固定相位的回波,即用s ij表示s ijexp(jΔΦij)。

2 方位多通道SAR多发多收模式的回波误差模型

在上述内容中,假设了各个通道的幅相特性一致,这样在幅相特性方面,多个通道的采样可以等效为单个通道的采样;还假设了实际的天线相位中心相较于测量值没有偏差,这样就可以达到等效采样位置在同一航线均匀分布的要求。然而,在工程实现时,以上两种理想条件均无法达到。由于各通道的前端组成部分(如天线、微波器件、A/D变换器等)的工作性能不可能完全一致,且这种不一致性会随着外界环境的变化而改变[4],所以各通道的幅相特性会不一致。设Γnr=γnrejζnr为第n个天线接收通道的幅相特性误差,Γnt=γntejζnt为第n个天线发射通道的幅相特性误差(以第一个天线的通道为参考,则γ1r=1,ζ1r=0,γ1t=1,ζ1t=0)。

同时,实际情况下天线的相位中心也总会偏离理想位置,造成等效后虚拟天线的相位中心与理想条件不一致。图2表示的是5个虚拟天线。

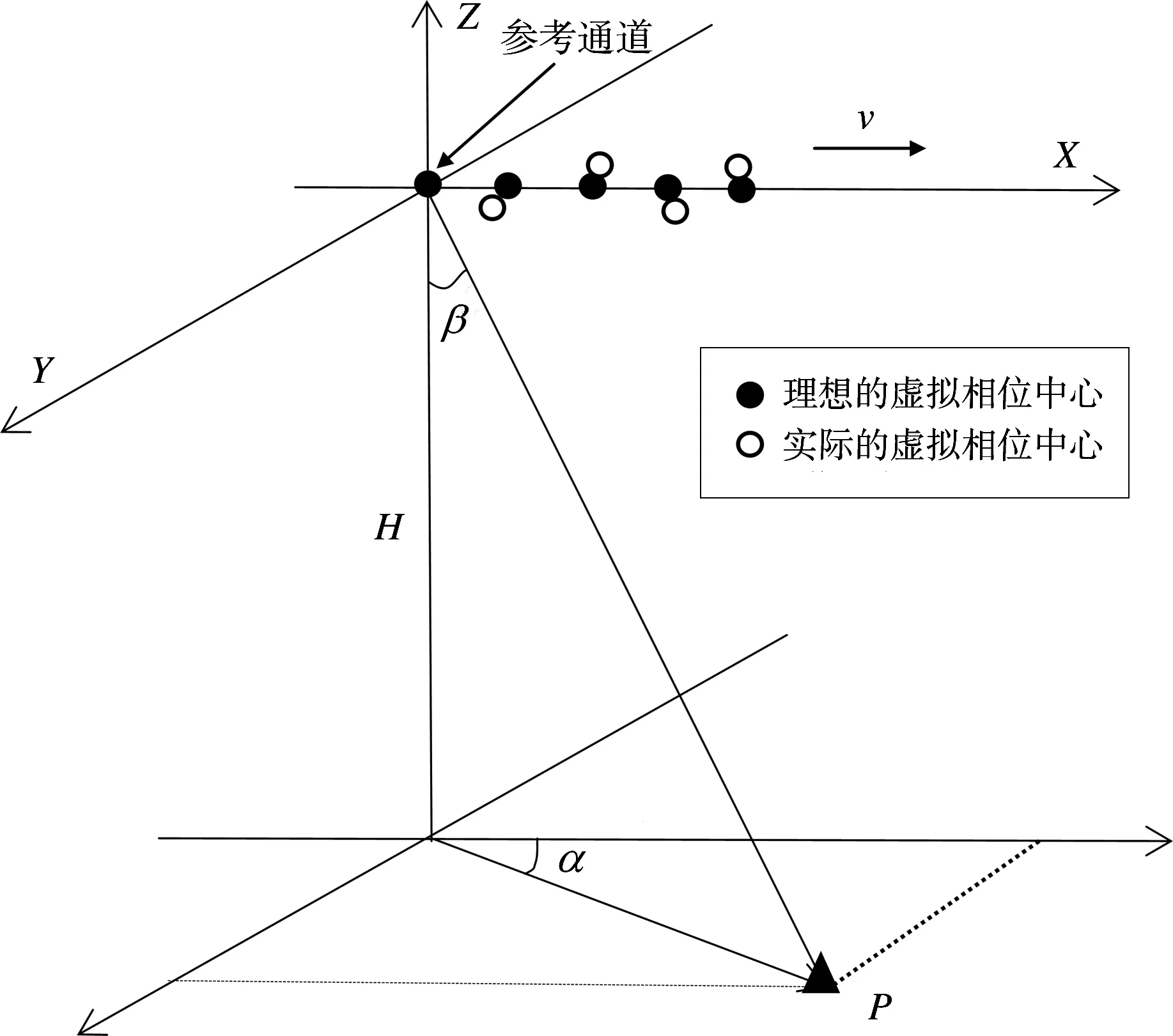
图2 相位中心误差示意图

首先定义方位向多通道SAR系统空间坐标系:X轴方向为卫星速度方向,Y轴方向垂直于X轴方向,Z轴背向地球中心。P点为目标点,β为最短斜距矢量与Z轴负方向的夹角,α为最短斜距矢量在地面投影与X轴方向的夹角。图中有3个天线,天线1坐标为(0,0,0)。实心点代表天线相位中心理想位置,均在X轴上,空心点代表天线相位中心实际位置,与理想位置有偏差。设第m个虚拟天线的相位中心偏差为(Δx m,Δy m,Δz m)(以天线1为参考,则有(Δx1,Δy1,Δz1)=(0,0,0))。显然,天线相位中心位置误差会使天线与目标的距离改变。当不存在天线相位中心位置误差时,第m个天线的相位中心坐标为(x m+vst,0,0)。设点目标的坐标为(x,y,z),则通道到点目标的距离为R m=当存在相位中心位置误差时,第m个天线的相位中心坐标为(x m+Δx m+vst,Δy m,Δz m),则到点目标的距离为对其进行泰勒级数展开,忽略误差小项的平方项、3次及3次以上的高次项,则距离历程可近似为

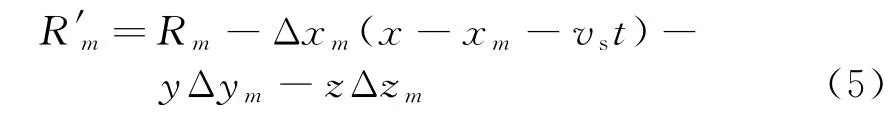
由式(5)可得出由相位中心偏差引起的相位误差为

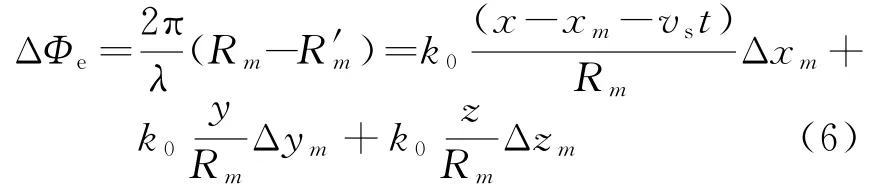
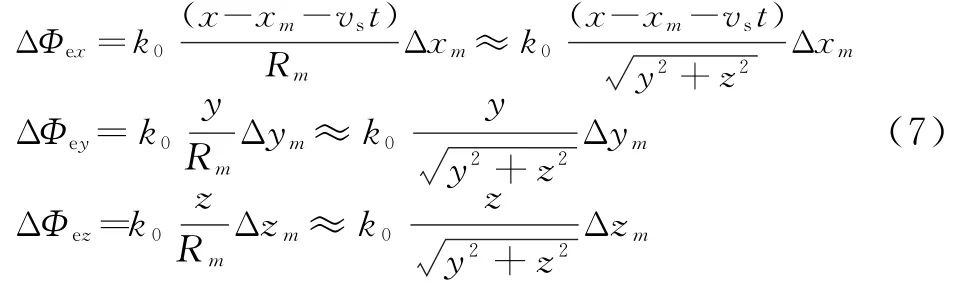
式中,ΔΦex为相位中心沿X轴方向的偏差Δx m引起的相位误差,ΔΦey为沿Y轴方向的偏差Δy m引起的相位误差,ΔΦez为沿Z轴方向的偏差Δz m引起的相位误差。其中,ΔΦex随方位向时间t变化,由文献[9],对于地面某一散射单元(x,y,z)的回波而言,方位慢时间域也为一线性调频信号,方位慢时间t与多普勒频率fa的关系为

代入式(7)得到

因此ΔΦex将随回波多普勒频率变化,而ΔΦey,ΔΦez可等效为通道的相位特性误差。需要补充说明的是,在多发多收模式下,同一虚拟天线相位中心可能是由不同的收发分置组合等效而来,则虚拟天线的相位中心误差Δx m需考虑到等效的来源,所以将(Δx m,Δy m,Δz m)改写为(Δx ij,Δy ij,Δz ij)。(Δx ij,Δy ij,Δz ij)表示第j个天线发射信号、第i个天线接收信号的收发分置组合所等效的虚拟天线的相位中心误差,则Δx ij=Δx i+Δx j,Δy ij=Δy i+Δy j,Δz ij=Δz i+Δz j,其中(Δx i,Δy i,Δz i)表示接收天线的相位中心误差,(Δx j,Δy j,Δz j)表示发射天线的相位中心误差。由式(7)、式(9)可得

3 幅相特性误差及天线相位中心误差对系统成像性能的影响

下面从理论上来分析通道特性误差和天线相位中心误差对系统成像性能的影响。因为本文研究的是误差对方位向的成像性能的影响,所以在接下来的分析中,将不考虑回波的距离向,只关注回波方位向信号,使分析过程简化至一维。本文参考了文献[4]的推导思路,针对多发多收模式,在回波信号中加入了相位中心误差。由文献[9]可知,回波方位向慢时间域也为一线性调频信号,因此可将方位向信号设为一个典型的线性调频信号。

设一个复数形式的线性调频信号[4]为

式中,η为方位慢时间,T a为脉冲宽度,K a表示该信号的调频率。由线性调频信号性质,该信号的带宽即多普勒带宽B a=K a T a。对s(η)进行采样,由奈奎斯特采样定理可知,当采样频率fs＞B a时,频谱不会发生混叠。在该系统中,多通道联合进行采样,由之前分析可知,每个通道的采样频率可以降为fs/M,M为虚拟天线数。设第m个虚拟天线采样得到的信号为s m(n),n=1,2,3,4,…。由方位多通道原理,需将各个通道采样得到的信号依次按方位向排列,即可得到等效为单通道对s(η)采样的信号s(n)。为了便于分析,将s m(n)每个采样点之间补上M-1个零,得到新的序列则有

这样就将向量组的排列转化为加法运算。由式(12)可得

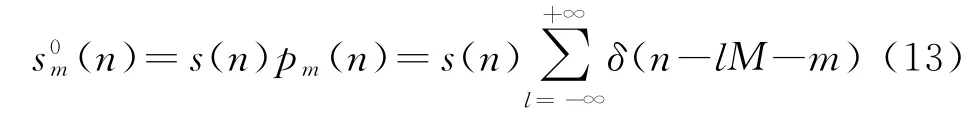
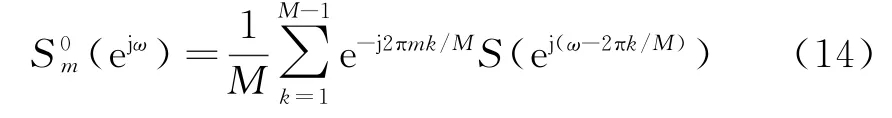
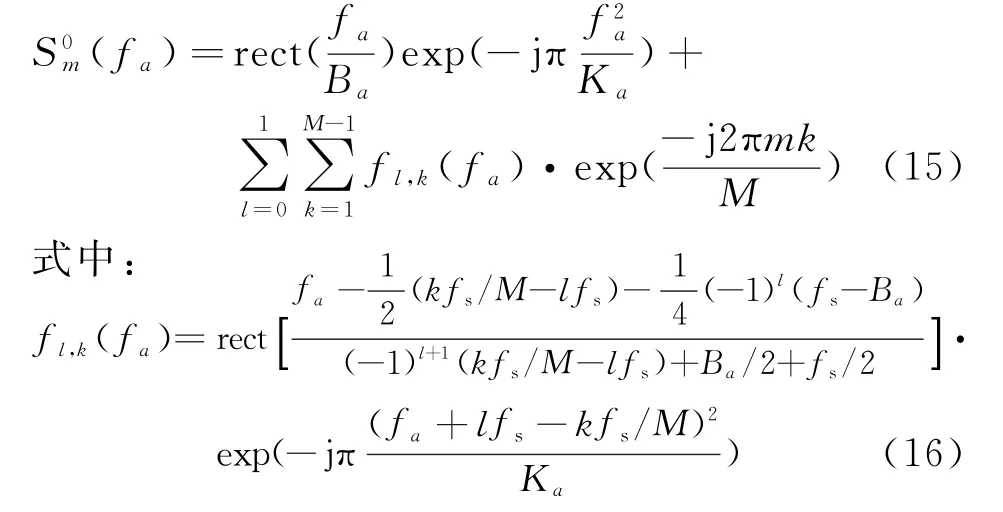
式中,lfs-kfs/M为方位模糊的频率偏移量,l决定方位模糊频谱偏移的正负,且l只取0和1是因为取其他值时方位模糊的频谱搬移将超过|f a|≤fs/2这一范围。下面将讨论加入幅相特性误差和天线相位中心误差后的方位向回波表达式。上文中,s ij为第j个发射机发射、第i个接收机接收,补偿相位后等效为自发自收的回波。现只考虑方位向,该信号可写为s ij(n),将其每个采样点之间补上M-1个零,得到以3个阵元为例,则有

式中,Γij=ΓirΓjtexp(jΔΦeyij)exp(jΔΦezij),m ij为第i个通道作接收通道和第j个通道作发射通道对应的虚拟天线次序。

由多发多收模式原理可知:

因此得到等效采样序列s(n)的频谱为

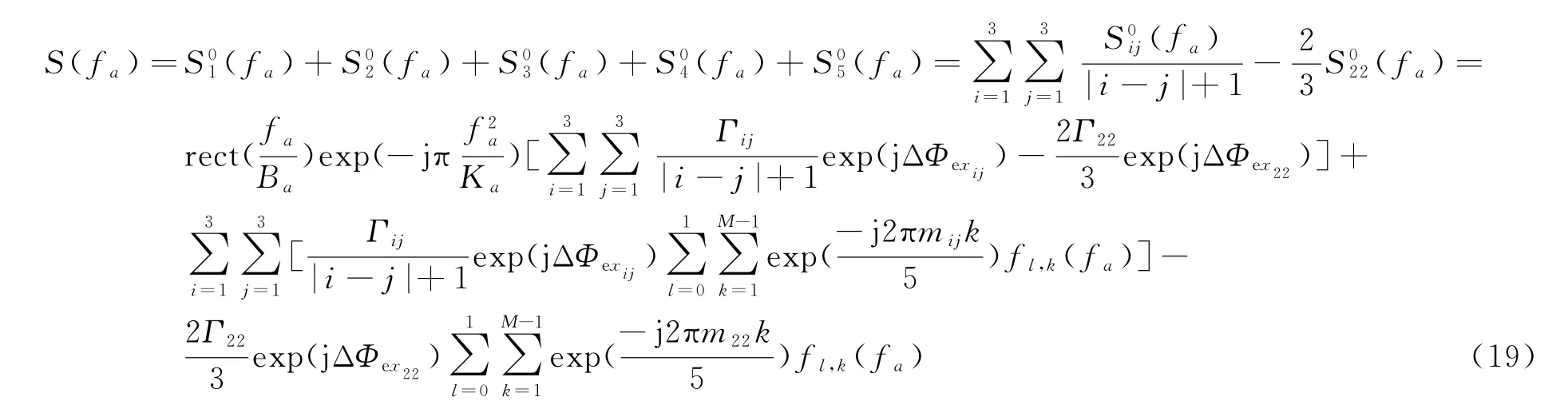
对S(f a)进行方位脉冲压缩,频域滤波器的表达式为

得到脉冲压缩的结果为

式中,q ij(η)为随着l,k,i,j变化的函数:

当通道特性一致,各天线无相位中心误差时,即Γij=1,(Δx ij,Δy ij,Δz ij)=(0,0,0),则式(21)可转化为

由式(29)可知,通道特性一致且无相位中心误差的情况下,成像结果无假目标存在。当通道特性不一致或由相位中心误差时,由式(21)可知,这种情况下有2(M-1)个假目标存在,假目标位置为

峰值-假目标比(假目标电平与真实目标电平大小的比值)的表达式为

由式(27)、式(28)可知,假目标在真实目标两侧成对出现,大小相等,位置对称。

4 仿真分析

下面利用仿真实验来分析通道幅相特性误差和天线相位中心误差对系统成像的影响,仿真参数如表1所示。整个实验分为两个部分:第一部分通过点目标成像的结果,直观地分析各类误差的影响,通过成像指标,包括峰值旁瓣比(PSLR)、积旁瓣比(ISLR)、分辨率展宽因子,定量地评价各类误差对系统成像的影响;第二部分验证上一节的数学推导结果。

表1 仿真参数

通过第3节的分析可知,通道幅相特性误差可分为幅度特性误差和相位特性误差。天线相位中心位置误差可分为沿X,Y,Z三个方向的误差,其中沿X方向的误差引起与多普勒频率有关的相位误差[12],沿Y,Z方向的误差产生常数相位误差,故可以将3个方向的相位中心位置误差分为沿航向(沿X方向)误差和沿垂直向(沿Y,Z方向)误差。设幅度特性误差、相位特性误差、沿航向和沿垂直向相位中心误差分别为在(0.8,1.2),(-π/2,π/2),(-d/4,d/4)范围内的随机数,参照表1的参数,分别加入各类误差进行点目标仿真。

图3(a)～图3(e)分别为不加误差和分别加入以上4类误差得到的点目标方位向截面图。

图3 点目标方位向截面图

由图3可知,对于方位向3个通道的系统,通道幅相特性误差和天线相位中心误差使得方位向上出现了8个虚假目标,验证了上节的推导。

图4～图7分别给出了通道幅度误差、通道相位误差和沿航向、沿垂直向的天线相位中心误差对点目标成像指标的影响,包括积分旁瓣比、峰值旁瓣比和分辨率展宽因子。假设各类误差均服从零均值高斯分布,横坐标为相应的均方差值,每个误差值均进行了100次统计实验,平均后得到成像性能指标。

图4 通道幅度误差对成像指标的影响

图5 通道相位误差对成像指标的影响

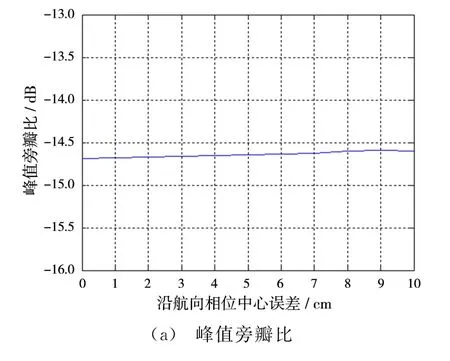
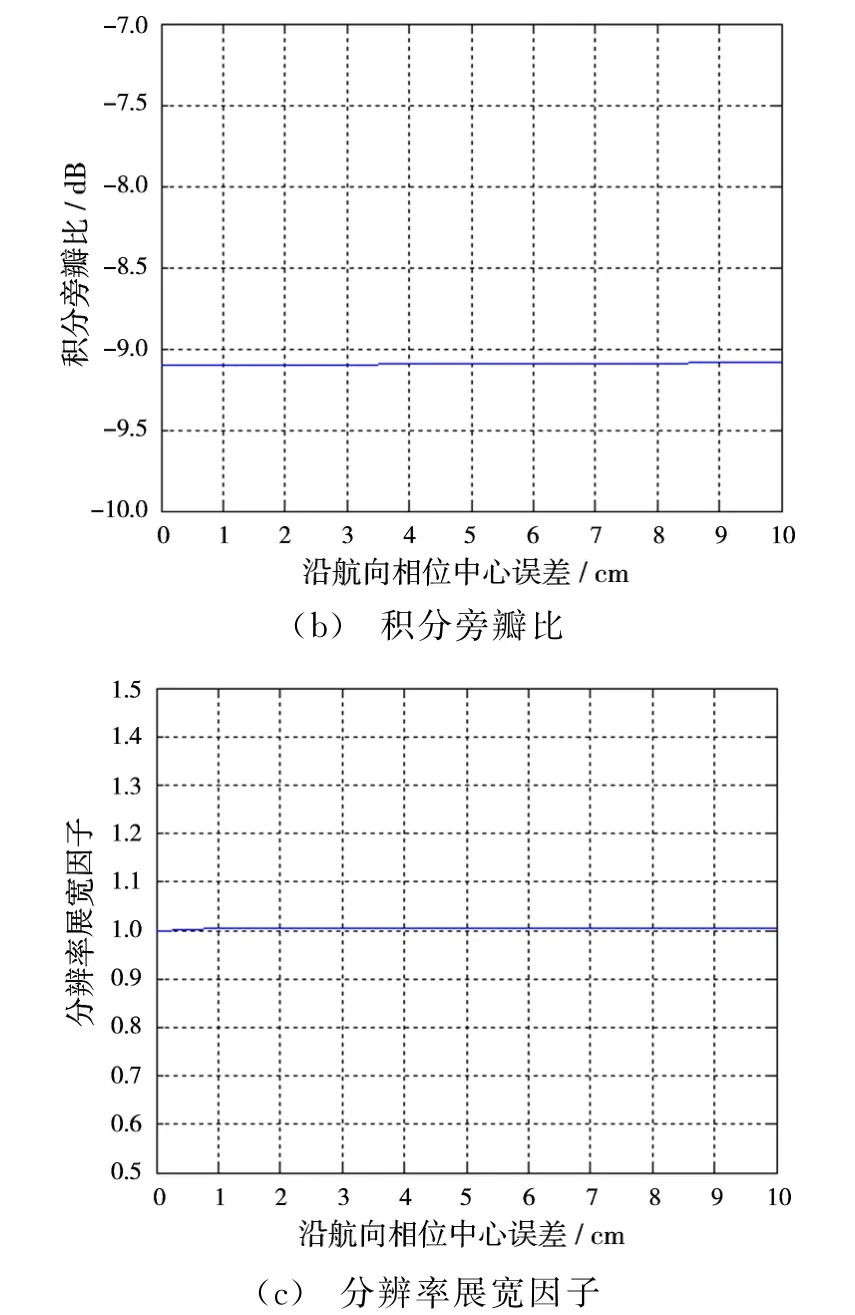
图6 沿航向相位中心误差对成像指标的影响

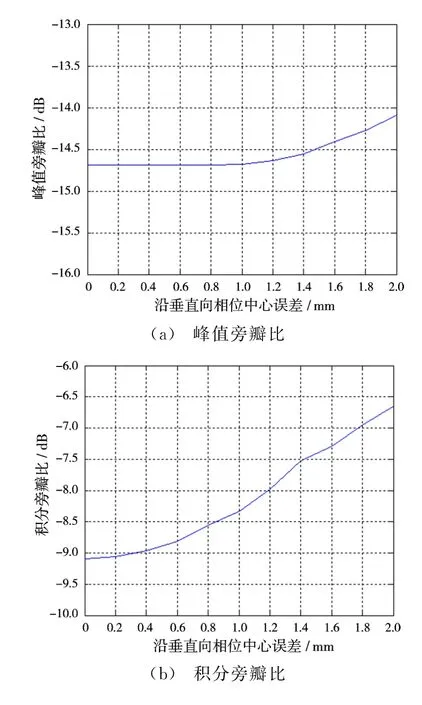
图7 沿垂直向相位中心误差对成像指标的影响

从图中可以看出,幅度误差主要影响积分旁瓣比,而对其他两项指标的几乎没有影响;通道相位误差主要影响积分旁瓣比,对分辨率几乎没有影响,相对于通道幅度误差,它对峰值旁瓣比影响略微明显;沿航向相位中心误差对3项指标的影响都较小,可以看到,即使当相位中心偏差10 cm时,峰值旁瓣比仅恶化0.08 dB,积分旁瓣比仅恶化0.01 d B,但它是4类误差中唯一一类对分辨率有明显影响的误差;沿垂直向的相位中心误差特别敏感,仅2 mm的误差就会使峰值旁瓣比恶化0.6 dB,积分旁瓣比恶化2.4 dB。

为验证上节推导的峰值-假目标比解析式,本文按照表1的参数进行方位向的一维仿真。为了便于将误差代入解析式计算,这里没有假设误差随机生成。设各通道幅度为γn=γ0(1+(-1)nΔγ),n=2,3,γ0为参考通道幅度,0≤Δγ≤0.2为幅度误差。各通道相位为ϕn=ϕ0(1+(-1)nΔϕ),n=2,3,ϕ0为参考通道相位,0°≤Δϕ≤10°为相位误差。各天线沿航向相位中心误差为Δx(0≤Δx≤5 cm),各天线沿距离向相位中心误差范围在(0,2)mm。以上误差均在范围内取9个值,分别代入解析式和加入回波模型进行成像仿真,得到理论值与仿真值两组曲线,进行对比,如图8所示。图中,虚线表示理论值,实线表示仿真值,纵轴为峰值假目标比,横轴为各类误差。仿真时,对称的两个假目标取电平较大者,因此在每类误差下得到4条曲线,分别对应4个假目标。

由图8可知,随着误差的增加,峰值-假目标比在升高,成像性能在恶化。通过对比仿真值和理论值两组曲线可知,理论值与仿真结果比较接近,从而证明了上节得出的峰值-假目标解析式的正确性。

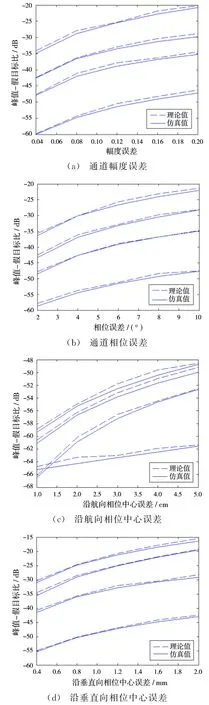
图8 峰值 假目标比仿真值与理论值对比

SAR系统存在以上分析的各类误差,会影响成像质量。在系统设计时,需要考虑利用内定标或外定标对以上误差进行估计。对于衡量误差是否在允许范围,本文的分析提供了一定的参考。由以上分析可知,系统的成像性能指标中,主要是积分旁瓣比受到了显著影响,因此这里只将积分旁瓣比的损失作为衡量误差的指标,提出参考建议。工程指标一般认为使积分旁瓣比损失1 d B以内的误差均可接受,由于本文是对每类误差进行单独分析,综合实际中各类误差同时存在,所以将可允许的积分旁瓣比损失定为0.5 dB。由图4(b)、图5(b)、图6(b)和图7(b)可知,对应的误差允许范围为:通道幅度特性误差不超过2 d B;通道相位特性误差不超过12°;沿航向相位中心误差影响较小,控制在一般范围内即可;沿垂直向相位中心误差不超过1 mm。

5 结束语

本文分析了多发多收模式下,通道幅相特性误差和天线相位中心误差对偏置相位中心方位向多通道SAR成像性能的影响。通过理论分析及数学推导,得出存在以上各类误差时,成像结果会出现假目标的结论,并得到了假目标位置和峰值-假目标比的计算公式。通过点目标仿真结果验证了公式的正确性,得出了各类成像性能指标随各类误差变化的曲线。

[1]杨桃丽.星载多通道高分辨宽测绘带合成孔径雷达成像处理技术研究[D].西安:西安电子科技大学,2014.

[2]BAUMGARTNER S V,KRIEGER G.Simultaneous High-Resolution Wide-Swath SAR Imaging and Ground Moving Target Indication:Processing Approaches and System Concepts[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2015,8(11):5015-5029.

[3]HONG F,WANG R,ZHANG Z,et al.Integrated Time and Phase Synchronization Strategy for a Multichannel Spaceborne-Stationary Bistatic SAR System[J].Remote Sensing,2016,8(8):628.

[4]郜参观,邓云凯,冯锦.通道不平衡对偏置相位中心多波束SAR性能影响的理论分析[J].电子与信息学报,2011,33(8):1828-1832.

[5]刘艳阳,李真芳,杨桃丽,等.一种单星方位多通道高分辨率宽测绘带SAR系统通道相位偏差时域估计新方法[J].电子与信息学报,2012,34(12):2913-2919.

[6]KIM H,CHANG Y K.Mission Scheduling Optimization of SAR Satellite Constellation for Minimizing System Response Time[J].Aerospace Science and Technology,2015,40(1):17-32.

[7]马仑,廖桂生,李真芳.多通道SAR误差估计与补偿方法及其实测数据验证[J].电子与信息学报,2009,31(6):1305-1309.

[8]ZHANG S,GUO Y,GOH C H,et al.A Novel Doppler Chirp Rate and Baseline Estimation Approach in Time Domain for Multi-Channel in Azimuth HRWS SAR System[C]∥IEEE 5th Asia-Pacific Conference on Synthetic Aperture Radar,Singapore:IEEE,2015:396-399.

[9]徐青.多通道雷达系统阵列误差校正方法研究[D].西安:西安电子科技大学,2011.

[10]LI Z,BAO Z,WANG H,et al.Performance Improvement for Constellation SAR Using Signal Processing Techniques[J].IEEE Trans on Aerospace and Electronic Systems,2006,42(2):436-452.

[11]宋岳鹏,杨汝良.应用多收发孔径实现高分辨率宽测绘带的合成孔径雷达研究[J].电子与信息学报,2007,29(9):2110-2113.

[12]马喜乐,孙造宇,董臻,等.方位多通道SAR信号重建性能分析[J].电子与信息学报,2014,36(3):545-551.