基于T-S模型的FNN降水粒子相态识别方法∗

李 海,邵海洲,章 涛,吴仁彪

(中国民航大学天津市智能信号与图像处理重点实验室,天津300300)

0 引言

云内降水粒子相态合理的识别在云降水物理、人工影响天气等领域具有非常重要的科学意义[1],不仅对了解水凝物在云中的生长和转换、提高定量降水的精确测量有重要的应用价值,而且能为人工影响天气的作业决策和评估提供重要的参考依据。传统的单偏振气象雷达由于只发射和接收单一方向的功率信息,因此得到的信息有限,限制了其对降水粒子相态识别的准确性。双线偏振气象雷达是一种新型的对云内降水粒子探测工具,由于同时发射和接收水平、垂直方向的偏振信息,因此较常规单偏振气象雷达,双线偏振气象雷达可以得到更多的偏振信息,其对降水粒子相态识别具有一定的优势[2]。

近年来,基于数学统计方法运用到双线偏振气象雷达对降水粒子相态识别的方法不断出现,包括统计决策[3]、判决图[4-5]、模糊逻辑方法[6-7]等。其中,统计决策理论是一种对降水粒子相态识别的可行算法,由于很难获得各降水粒子的先验概率和概率密度函数,使得数据模型很难建立,进而影响其对降水粒子的相态识别[3];判决图方法是一种基于布尔逻辑的算法,该方法根据预先确定的类型边界来进行分类,但是气象雷达接收到的不同降水粒子的协方差矩阵不是相互独立的,对降水粒子分类精度有一定的影响[5];相较上述两种方法,模糊逻辑方法[8-10]对不同降水类型各偏振参量建立隶属函数和规则基,解决了回波信号间相互排斥的问题,在降水粒子的相态识别方面具有一定的优势,但是不同降水类型各偏振参量隶属函数的参数一般采用经验值,使得其对降水粒子相态识别性能不稳定[11]。

基于上述问题,本文提出一种基于T-S模型的模糊神经网络降水粒子相态识别方法。该方法通过建立一种多层前馈的神经网络,首先对双线偏振气象雷达接收的偏振参量进行模糊化、规则计算、模糊推理和退模糊处理,然后利用模糊神经网络误差反馈的思想自适应地调节模糊化过程中不同降水类型各偏振参量隶属函数参数,最后对感兴趣的降水粒子相态进行识别。相较传统的模糊逻辑方法,本文方法能够很好地对降水粒子相态进行识别和更好地反映天气情况。

1 T-S模型的模糊神经网络降水粒子相态识别方法

模糊神经网络是近些年发展起来的一种新型网络结构,具有模糊逻辑系统和神经网络的双重优点,且收敛速度快。本文提出的基于T-S模型的模糊神经网络由前件网络、后件网络和反馈网络三部分组成,如图1所示。

图1 T-S模型的模糊神经网络

1.1 前件网络

前件网络包括输入层和隐含层。前件网络的作用是对输入的偏振参量进行模糊化、规则计算、归一化处理,为后件网络提供连接权值。

在输入层中,输入值为x1,x2,x3,x4。其分别表示双线偏振气象雷达的各偏振参量:反射率因子ZH,差分反射率因子ZDR,差分相移率KDP,互相关系数ρHV。

隐含层包括模糊化层和规则计算层。

在模糊化层中,对各偏振参量进行模糊化处理,建立不同降水类型各偏振参量的隶属函数如图2所示,钟型隶属函数具有一个宽泛的平坦区域,两端有较宽的过渡区,其可以改善降水粒子相态识别的鲁棒性。此外,钟型隶属函数是连续的,对于模糊神经网络训练学习来计算不同降水类型各偏振参量隶属函数参数修正参量是可行的。

式中,x j(j=1,2,3,4)是双线偏振气象雷达的第j个偏振参量是第j个偏振参量对应第i(i=1,2,…,8,本文假设存在8种降水类型)类降水类型的隶属函数曲线中心是第j个偏振参量对应第i类降水类型的隶属函数曲线宽度是第j个偏振参量对应第i类降水类型的隶属函数曲线斜率,隶属函数是一个在[0,1]之间的数越接近于0,表示第j个偏振参量x j属于第i类降水的程度越小;反之,其越靠近1,表示第j个偏振参量x j属于第i类降水类型的程度越大。

图2 钟型隶属函数

在规则计算层,每个节点代表一条模糊规则,对待识别的降水粒子各偏振参量的隶属函数进行模糊计算,可计算得到待识别降水粒子隶属于不同降水类型的规则适用度R。待识别的降水粒子隶属于第i类降水类型的规则适用度R i可由下式计算得到:

对R i进行归一化处理,计算得到归一化后的结果¯R i,并将其作为连接权值传输到后件网络的隐含层:

1.2 后件网络

后件网络包括输入层、隐含层和输出层。后件网络接收由前件网络传输进来的降水粒子规则适用度,结合后件网络的模糊推理结果计算每种降水类型的聚类中心。

在后件网络的输入层中,输入可表示为

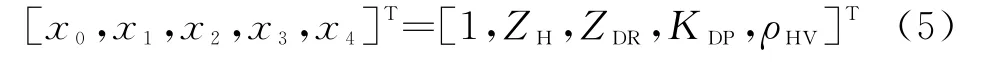
式中,第0个节点的输入值x0=1,其作用是提供模糊规则后件中的常数项。

后件网络的隐含层由r个结构相同的并列子网络组成,每个子网络产生一个输出量。每个子网络拥有i个节点数,每个节点数代表一条模糊推理。该推理规则如下:

此时,有下式成立:

式中,y ri(i=1,2,…,8)为后件网络的第r个子网络中第i类降水类型的模糊推理值为第r个子网络的权值系数为第j个偏振参量对应第i类降水类型隶属函数值的模糊集。后件网络的隐含层输出如下式所示:

网络的输出y可表示为

1.3 反馈网络

反馈网络的作用是计算不同降水类型各偏振参量的隶属函数参数值。在反馈网络中,首先对后件网络的输出结果进行退模糊处理,然后结合不同降水类型聚类中心的先验信息,返回前件网络的模糊化层,自适应地调节不同降水类型各偏振参量隶属函数参数。

后件网络的子网络输出y k(k=1,2,…,r)是一个模糊集合,为了在降水粒子相态中找到最能代表模糊集合输出的清晰值,需对其进行退模糊处理。本文利用最大集成法把最大真值的结果作为最终结果,即C=Max(y k)。对于假设存在的8种降水类型,建立如表1所示的8种降水类型聚类中心C ei索引表。

表1 8种降水类型聚类中心Cei索引表

在建立的T-S模型的模糊神经网络中,利用误差反馈的思想对网络学习。在模糊神经网络中对前件网络模糊化层中的不同降水类型各偏振参量隶属函数参数重新计算,得到不同降水类型各偏振参量新的隶属函数参数,分别用表示,下面给出推导过程。

取降水粒子聚类中心代价函数为

式中,C ei为第i类降水类型网络期望输出的聚类中心,C i为第i类降水类型网络实际输出的聚类中心,e i为第i类降水类型的聚类中心期望输出和实际输出的误差。

当第i类降水类型聚类中心的实际输出值与期望输出值不一致时,则从后件网络的输出层返回前件网络的模糊化层,对不同降水类型各偏振参量隶属函数参数重新计算。模糊化层中第i类降水类型的第j个偏振参量隶属函数参数的修正参量用下式进行计算[11]:

式中,l aij,l bij,l cij分别为第i类降水类型的第j个偏振参量隶属函数参数的训练权值[11]。

根据式(12)～式(14)计算得到的不同降水类型各偏振参量隶属函数参数的修正参量更新原隶属函数参数,更新后的不同降水类型各偏振参量隶属函数参数分别为可由下式计算得到:

模糊神经网络学习结束后,利用计算得到的不同降水类型各偏振参量隶属函数参数建立新的隶属函数,对感兴趣的降水粒子进行相态识别。

2 方法流程及实现步骤

本文方法流程图如图3所示,具体操作步骤如下。

图3 本文方法流程图

步骤1 建立T-S模型的模糊神经网络。该网络由前件网络、后件网络和反馈网络三部分组成。前件网络由输入层和隐含层中的模糊化层和规则计算层组成。后件网络由输入层和隐含层的模糊推理层以及输出层组成。反馈网络的功能是对模糊神经网络进行学习训练,自适应地调节不同降水类型各偏振参量隶属函数参数。

步骤2 网络初始化。对前件网络模糊化处理过程中不同降水类型各偏振参量隶属函数参数进行初始化处理,即给不同降水类型各偏振参量隶属函数参数设置初始值,为了使得网络快速地收敛,在对不同降水类型各偏振参量隶属函数初始化时采用文献[12]和文献[13]的隶属函数参数经验值作为其初始化值。在输出层,对不同降水类型聚类中心初始化,不同降水类型的聚类中心初始值如表1所示。

步骤3 利用多组双线偏振气象雷达探测降水的回波样本对网络初始化后的模糊神经网络训练学习。在前件网络中对输入层偏振参量(ZH,ZDR,KDP,ρHV)进行模糊化,规则计算处理,计算降水粒子隶属于不同降水类型的规则适用度。在后件网络中,计算各降水粒子的聚类中心,并对其进行退模糊处理。在反馈网络中,将退模糊后的降水粒子聚类中心与网络期望输出的降水类型聚类中心比较,如果不一致,则返回前件网络的模糊化层,通过误差反馈的思想自适应调节不同降水类型各偏振参量隶属函数参数。

步骤4 利用步骤3中模糊神经网络训练学习得到的不同降水类型各偏振参量隶属函数参数并建立相应的隶属函数,对感兴趣的降水粒子进行相态识别。

3 实验与结果分析

本文采用美国俄克拉荷马州的WSR-88D雷达(KTLX)不同时刻扫描得到的多组LEVEL-II实测数据对模糊神经网络训练学习,计算不同降水类型各偏振参量隶属函数参数。利用模糊神经网络训练计算得到的不同降水类型各偏振参量隶属函数参数建立相应隶属函数,分别对KTLX双线偏振气象雷达的一次冰雪云降水(2015年5月13日,19∶30,GMT)和CSAPR双线偏振气象雷达一次强对流降水(2011年5月20日,11∶01,GMT)的相态进行识别,验证所提降水粒子相态识别算法的性能。

3.1 模糊神经网络训练

将KTLX雷达不同时刻(2015年5月13日,19∶00—19∶29,GMT)接收的1450组降水数据作为训练样本,对本文建立的基于T-S模型的模糊神经网络训练学习,计算不同降水类型各偏振参量(ZH,ZDR,KDP,ρHV)隶属函数参数。表2为本文方法计算得到的8种降水类型各偏振参量隶属函数参数。

表2 8种降水类型的各偏振参量隶属函数参数

图4分别给出了4个偏振参量(ZH,ZDR,KDP,ρHV)对应8种降水类型的共计32个隶属函数。本文利用多组降水数据对模糊神经网络训练学习来自适应地调节隶属函数参数,经模糊神经网络训练学习后的不同降水类型各偏振参量隶属函数参数符合Straka[4]和Ryzhkov[14]等对不同降水类型偏振特性的研究成果。例如,冰雹(H A)的ZH和其尺寸大小、粒子数量有关,ZH值在50 dBz附近;冰雹降落时趋向于翻滚运动,形状接近于球形,ZDR值一般在0 d B左右;由于冰雹粒子降落时各相同性,KDP值接近0°/km;冰雹在降落过程中的翻滚运动也使得返回的水平和垂直偏振信号的相关性较差,ρHV值在0.9附近。

图4 8种降水类型各偏振参量(ZH,ZDR,KDP,ρHV)隶属函数

3.2 冰雪云降水粒子相态识别及结果分析

选取美国俄克拉荷马州的KTLX雷达(2015年5月13日,19∶30,GMT)在降雨模式下捕获的一块降水区域(600 km×600 km),该降水区域的雷达回波基本产品包括反射率因子ZH、差分反射率因子ZDR、差分相移ΦDP和互相关系数ρHV。各偏振参量读取结果如图5所示。图6为美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration,NOAA)提供的KTLX雷达PPI模式下各偏振参量(ZH,ZDR,ΦDP,ρHV)显示结果。NOAA作为美国权威的气象预报部门,本文对KTLX雷达的数据处理结果以NOAA提供的雷达显示为参考。将图5和图6结果进行比较可见,本文读取各偏振参量的结果与NOAA提供的各偏振参量结果一致。

因为差分相移率KDP不是WSR-88D双线偏振气象雷达直接测量的参量,可以通过差分相移ΦDP计算得到,本文采用文献[15]方法计算差分相移率KDP。KDP计算结果如图7所示。图8为NOAA提供的KDP显示结果。将图7和图8结果进行比较可见,由文献[15]计算得到的KDP结果与NOAA提供的KDP结果一致。

图5 本文读取的KTLX雷达回波偏振参量(方位角:0.5°)

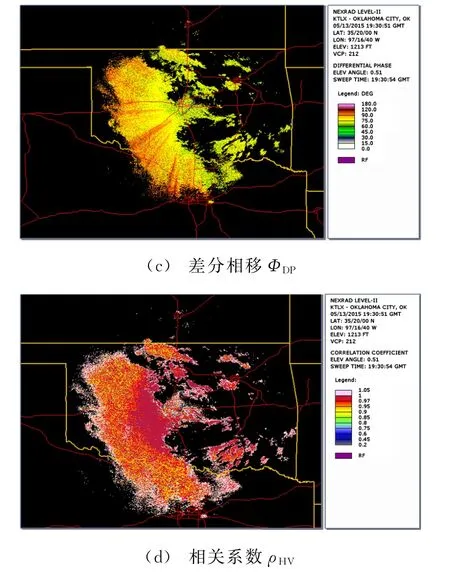
图6 NOAA提供的KTLX雷达PPI模式下各偏振参量显示(方位角:0.51°)

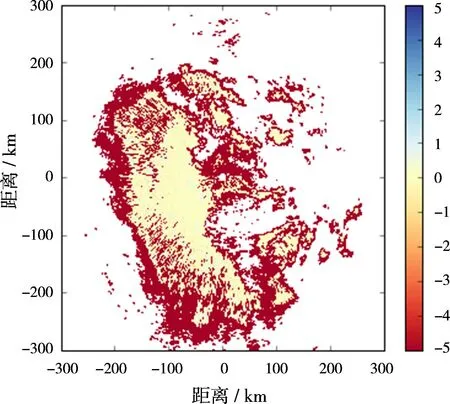
图7 差分相移率KDP

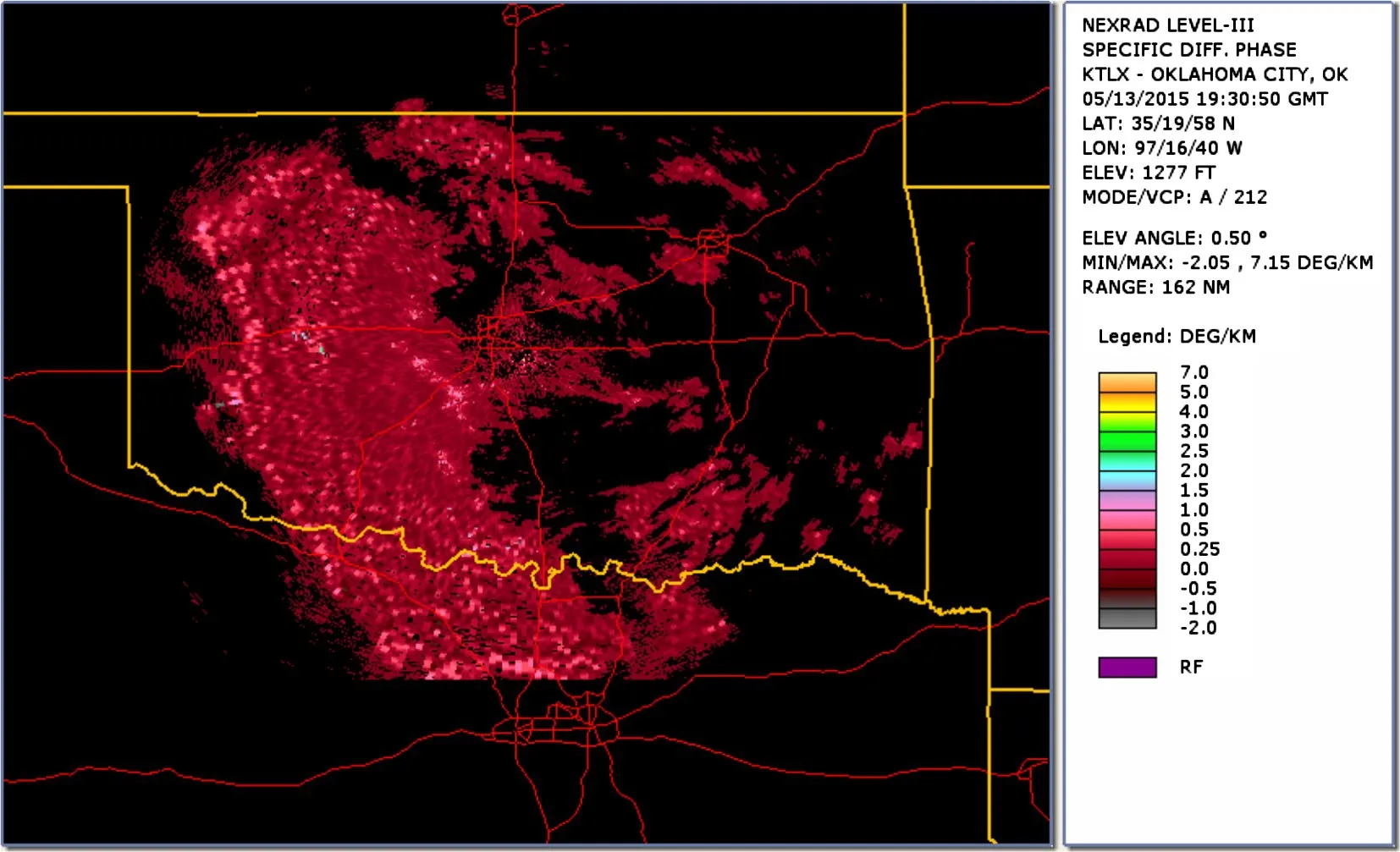
图8 NOAA提供的KDP显示结果

对KTLX雷达(2015年5月13日,19∶30,GMT)各偏振参量(ZH,ZDR,KDP,ρHV)利用网络训练得到参数建立的隶属函数进行模糊化、规则计算、模糊推理和退模糊处理,识别降水粒子相态,降水粒子相态识别结果如图9所示。图10为NOAA提供的本次降水的降水粒子相态识别结果。由图9和图10比较可见,在距离KTLX双线偏振气象雷达半径100 km的距离范围内,毛毛雨(DR)和雨(RA)的相态被有效区分开;此外,在距离KTLX双线偏振气象雷达220 km附近被湿雪粒子(WS)信号淹没的冰晶粒子(IC)相态得到有效识别。

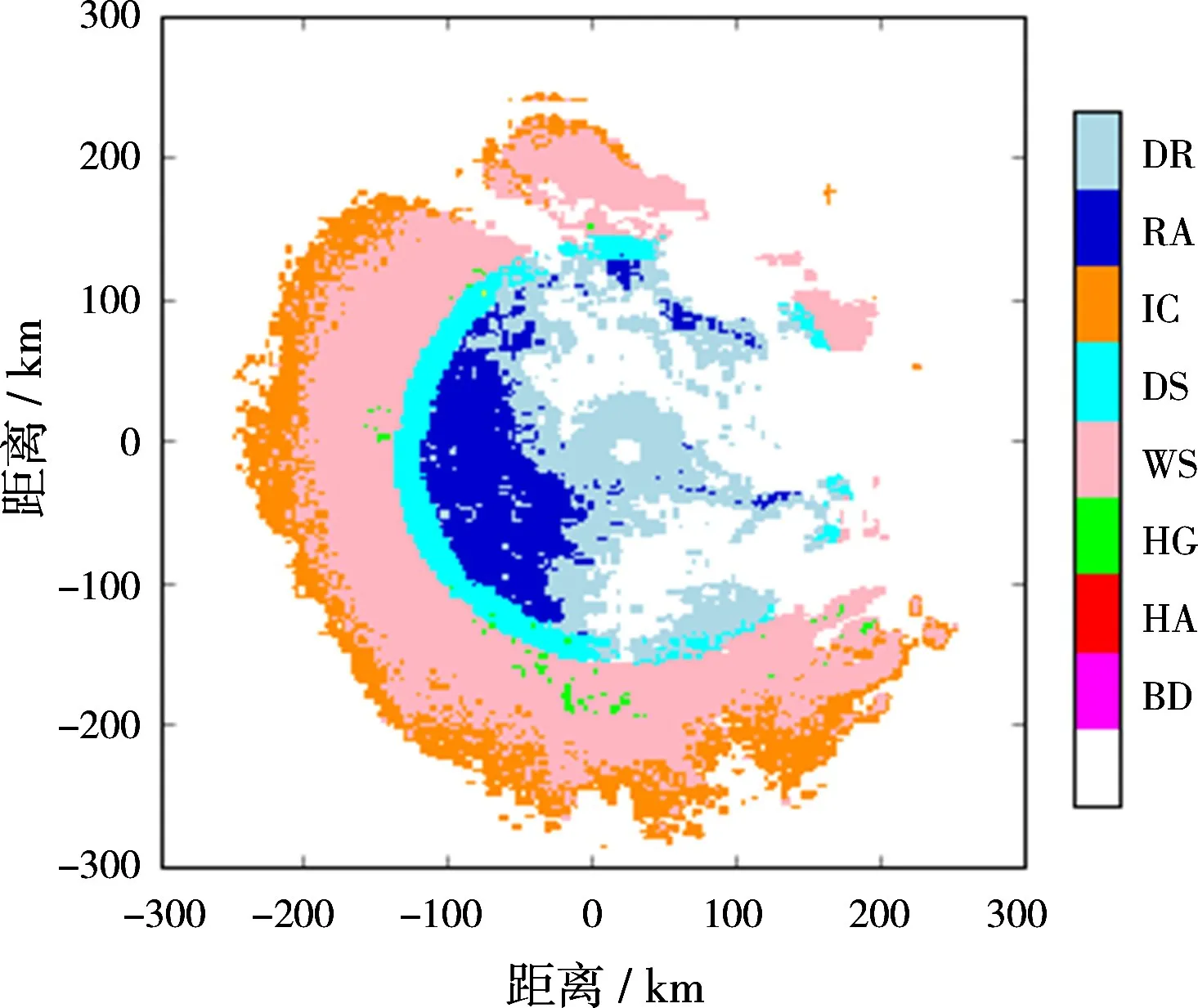
图9 本文方法降水粒子相态识别结果

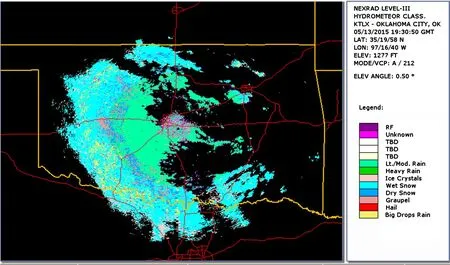
图10 NOAA提供的降水粒子相态识别结果

3.3 强对流降水粒子相态识别结果及分析

选取美国俄克拉荷马州CSAPR双线偏振气象雷达(2011年5月20日,11∶01,GMT)在强对流降雨模式下捕获的一块降水区域(240 km×240 km),该降水区域的雷达回波基本产品包括反射率因子ZH、差分反射率因子ZDR、差分相移率KDP和互相关系数ρHV。各偏振参量读取结果如图11所示。

图11 CSAPR雷达回波偏振参量(方位角:0.8°)

利用训练好的模糊神经网络对CSAPR雷达(2011年5月20日,11∶01,GMT)接收到的降水粒子进行相态识别,降水粒子相态识别结果如图12所示。图13为美国大气辐射测量机构(Atmospheric Radiation Measurement,ARM)提供的本次强对流降水的降水粒子相态识别结果。由图12和图13比较可见,本文建立的8种降水类型可以更精细化地对降水粒子相态进行识别。例如毛毛雨(DR)和强降雨(RA)的相态得到有效区分;此外,被强降雨(RA)信号淹没的干雪(DS)粒子相态得到有效识别。

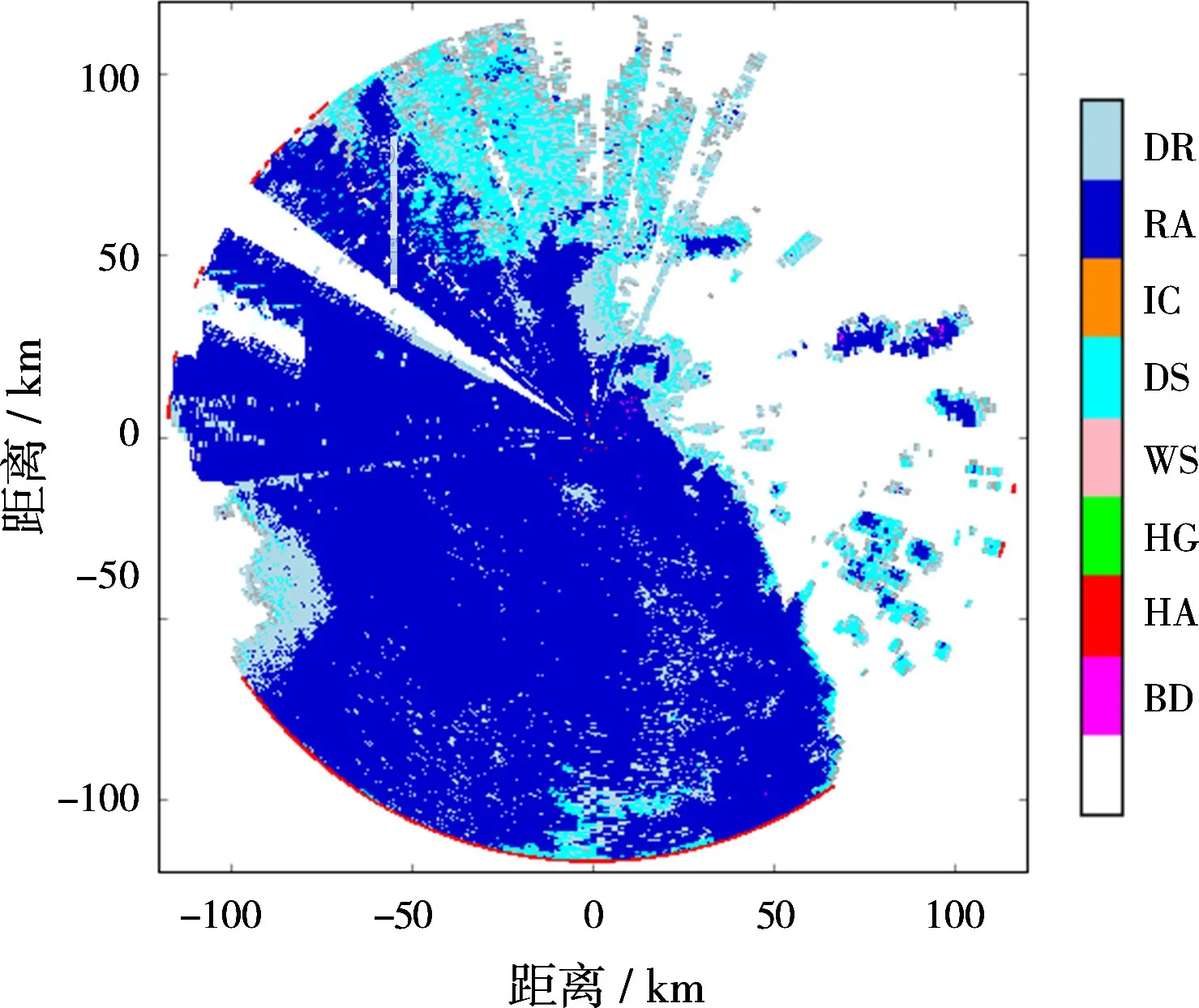
图12 本文方法降水粒子相态识别结果

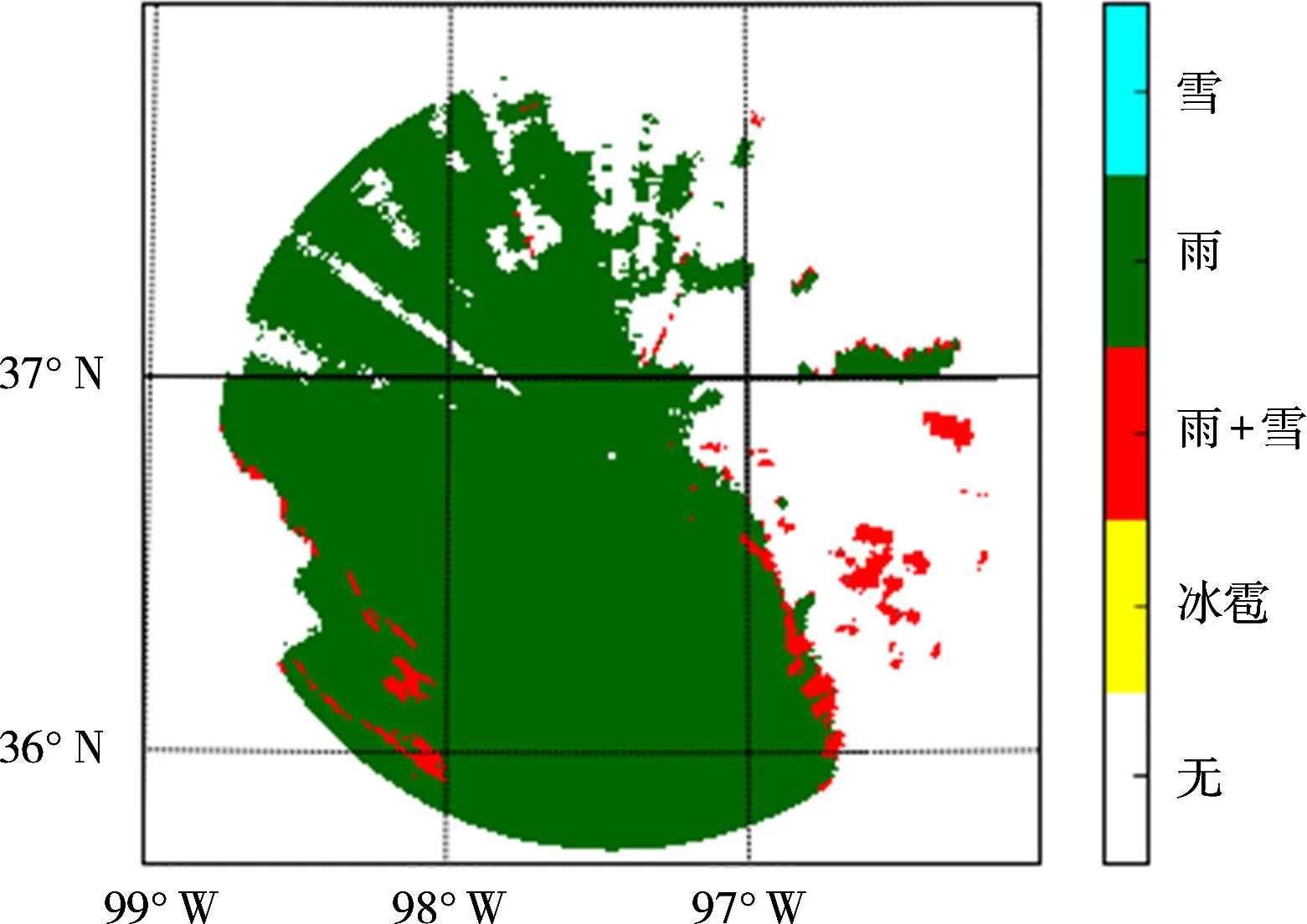
图13 ARM提供的降水粒子相态识别结果

4 结束语

针对降水粒子相态识别过程中不同降水类型各偏振参量建立隶属函数时参数使用经验值,不能有效反映真实降水粒子相态的问题,本文提出一种基于T-S模型的模糊神经网络降水粒子相态识别方法。该方法在传统的模糊逻辑系统基础上,建立一种多层前馈的模糊神经网络,利用多组降水样本对模糊神经网络训练学习,自适应地调节不同降水类型各偏振参量隶属函数参数,进而对感兴趣的降水粒子进行相态识别。通过实测数据的处理结果验证了本文所提降水粒子相态识别方法的有效性。

[1]刘黎平,胡志群,吴翀.双线偏振雷达和相控阵天气雷达技术的发展和应用[J].气象科技进展,2016,6(3):28-33.

[2]MAHALE V N,ZHANG G F,XUE M.Characterization of the 14 June 2011 Norman,Oklahoma,Downburst through Dual-Polarization Radar Observations and Hydrometeor Classification[J].Journal of Applied Meteorology and Climatology,2016,55(12):2635-2655.

[3]黄钰,阮征,郭学良,等.垂直探测雷达对北京地区夏季降水分类统计[J].高原气象,2016,35(3):745-754.

[4]STRAKA J M,ZRNIC D S.An Algorithm to Deduce Hydrometeor Types and Contents from Multi-Parameter Radar Data[C]∥26th Conference on Radar Meteorology,Boston,MA:American Meteorological Society,1993:513-515.

[5]HOLLER H,BRINGI V N,HUBBERT J.Life Cycle and Precipitation Ormation in a Hybrid-Type Hailstorm Revealed by Polarimeteric and Doppler Radar Measurements[J].Journal of the Atmospheric Science,1994,51(17):2500-2522.

[6]LEE J K,KIM H L,KIM J H.Case Study of the Hydrometeor Classification with the S-Band Dual-Polarization Radar[J].Journal of Korean Society of Hazard Mitigation,2014,14(5):57-66.

[7]PARK H,RYZHKOV A V,ZRNIC D S,et al.The Hydrometeor Classification Algorithm for the Polarimetric WSR-88D:Description and Application to an MCS[J].Weather and Forecasting,2008,24(3):730-746.

[8]BECHINI R,CHANDRASEKAR V.A Semisupervised Robust Hydrometeor Classification Method for Dual-Polarization Radar Applications[J].Journal of Atmospheric and Oceanic Technology,2015,32(1):22-47.

[9]曹俊武,刘黎平.双线偏振雷达判别降水粒子类型技术及其检验[J].高原气象,2007,26(1):116-127.

[10]何宇翔,肖辉,吕达仁.利用极化雷达分析层状云中水凝物粒子性状分布[J].大气科学,2010,34(1):23-34.

[11]许哲万,李晶皎,王爱侠,等.一种基于改进T-S模糊推理的模糊神经网络学习算法[J].计算机科学,2011,38(11):196-199.

[12]RYZHKOV A V,GIANGRANDE S E,MELNIKOV V M,et al.Calibration Issues of Dual-Polarization Radar Measurements[J].Journal of Atmospheric and Oceanic Technology,2004,22(8):1138-1155.

[13]KOUKETSU T,UYEDA H,OHIGASHI T,et al.A Hydrometeor Classification Method for X-Band Polarimetric Radar:Construction and Validation Focusing on Solid Hydrometeors Under Moist Environments[J].Journal of Atmospheric and Oceanic Technology,2015,32(11):2052-2074.

[14]RYZHKOV A,ZRNIC D S,BURGESS D,et al.Observation and Classification of Echoes with the Polarimetric WSR-88D Radar[R].Norman,Oklahoma:National Servere Storms Laboratory,2003.

[15]HUANG H,ZHANG G,ZHAO K,et al.A Hybrid Method to Estimate Specific Differential Phase and Rainfall with Linear Programming and Physics Constraints[J].IEEE Trans on Geoscience and Remote Sensing,2016,55(1):96-111.