基于主动磁轴承的机床切削系统动态特性分析

方朋杰 乔晓利,2

(1.绍兴文理学院 元培学院,浙江 绍兴 312000;2.浙江大学 电气工程学院,浙江 杭州 310027)

0 引言

数控机床正在朝着高速度、高精度、高效、高智能化的方向发展.机床高速化是继数控加工技术之后制造技术的又一次革命性飞跃，已成为现代制造技术发展的重要方向，具有切削速度高、运转平稳、切削效率高、散热快、表面精度高等优点.

作为支承高速高档机床电主轴的主动磁悬浮支承技术，被公认为是当前世界上的高新技术之一.主动磁悬浮轴承利用磁场力将主轴部件悬浮于空间，即转子与定子无直接接触，工作时不产生机械摩擦,具有零润滑、零振动、无噪声及温升小等优点.人们可通过改变控制器参数的方法来调整主动磁轴承的支承刚度和阻尼，从而改变其对电主轴转子的支承特性，进而改变电主轴转子的动力学特性.

电主轴转子转速的升高使得磁悬浮电主轴的运行稳定性变差,这是由于在高速情况下，电主轴转子表现出来的柔性特性，使得电主轴切削系统的动态性能复杂化，从而使切削系统稳定性变差.鉴于此，对主动磁轴承支撑的柔性电主轴转子系统动力学特性的研究被很多学者关注.近几年也有不少的学者研究柔性电主轴的动态特性，如Zhang Lingling,Wan Min等人借用ANSYS软件分析了柔性电主轴的动态特性[1-2].关于磁悬浮柔性电主轴动态特性的研究还较少.2014年，Xie Zhenyu研究了主动磁轴承结构对柔性电主轴的影响[3],Xu Xin等人研究了低损耗的磁悬浮柔性电主轴[4]等.文献[5]研究了主轴及磁轴承缺陷对磁悬浮电主轴系统动态特性的影响.文献[6]主要对磁悬浮电主轴的切削参数及振动特性进行了分析和研究.Barkallah,M.等[7]主要研究了参数(切削率、切削速度及轴向切削深度)对切削力及铣削过程中颤振的影响.Huang Tao等[8]主要研究了如何对铣削过程中的颤振进行主动控制.

在高速机械加工过程中，切削过程是否稳定，不仅取决于高速磁悬浮电主轴转子系统的动力特性，还取决于切削过程的动力特性，二者又不是完全独立的系统，它们互相作用，互相影响.因此，必须把机械加工过程中的动态切削特性与磁悬浮柔性电主轴转子系统的特性结合起来，研究整个系统的动态特性，才能得出较科学的理论根据，而这在国内外未见有人研究.

为此，本文综合主动磁轴承的可控特性和切削过程的动态特性，深入研究了柔性电主轴转子在主动磁轴承及动态切削的影响下的动力学特性.

1 主动磁轴承的工作原理

一个简化的主动磁轴承控制原理图如图1所示，转子自由悬浮在所设定的(x0,y0)处，非接触式位置传感器实测转子的实际位置(x,y)与设定位置(x0,y0)之间的偏差，并反馈至控制器.控制目标为维持转子在期望值(x0,y0)附近.为此，根据转子的实际位置(x,y)与设定位置(x0,y0)之间的偏差信号，控制器发出位置调整指令信号，功率放大器将该信号转换为电流输入轴承电磁铁线圈中，使其产生所需的控制电磁力(Fm,x,Fm,y)，从而使转子稳定悬浮[10].

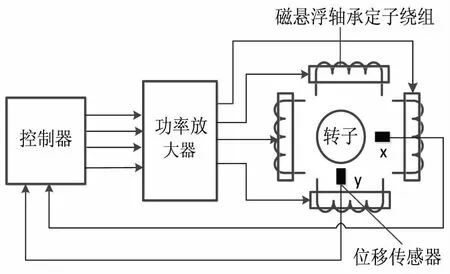
图1 主动磁轴承工作原理

2 主动磁轴承支承下柔性电主轴切削系统的动力学模型

2.1 主动磁轴承-柔性电主轴切削系统的有限元模型

由主动磁轴承支撑的柔性电主轴切削系统的简化结构如图2所示.该系统的主要部件有：高速电机转子、粗细不等的弹性电主轴轴段、主动磁轴承、刀具等.在建立基于主动磁轴承支撑的柔性电主轴切削系统有限元模型时，假设电机的转子、刀具夹及刀具的材料都是各向同性的.

把不同粗细的轴段、磁轴承、刀具等沿电主轴中心轴线划分为不同的单元，磁轴承的特性和动态切削过程以力的形式施加在电主轴转子相应的节点上.以电主轴转子的中心轴线为z轴，xy平面是垂直于z轴建立的oxyz坐标系平面，主动磁轴承柔性电主轴切削系统的有限元模型为[9]：

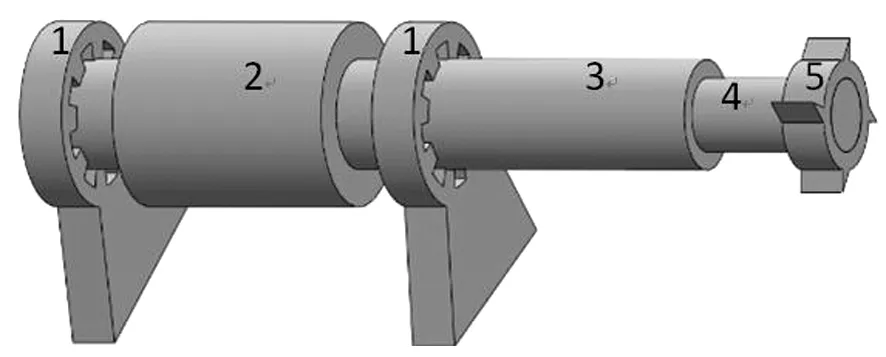
1—磁轴承；2—转子；3—电主轴；4—刀具夹；5—刀具图2 磁轴承-柔性电主轴简化结构

(1)

式中：Ms为质量矩阵，Ks为刚度矩阵，Ds为阻尼矩阵，Gs为陀螺矩阵，Ωs为电主轴稳态工作转速;Fcu,x和Fcu,y分别为刀具与工件之间的切削力在x和y方向上的量，Fam,x和Fam,y分别为主动磁轴承径向电磁控制力在x和y方向上量，n为单元节点的总个数.下标x和y分别表示坐标轴的x和y方向.

式(1)中的刚度和阻尼主要指由主动磁轴承及控制器产生的等效刚度和阻尼、电主轴转子的刚度和结构阻尼及动态切削过程中的刚度和阻尼.

2.2 主动磁轴承的等效电磁力模型

主动电磁轴承的等效电磁力模型在有关书籍及文献中已有详细推导，这里就不再推导其过程.本文仍然采取差动的电磁结构建立主动电磁力模型[12].差动控制结构电磁轴承如图3所示.

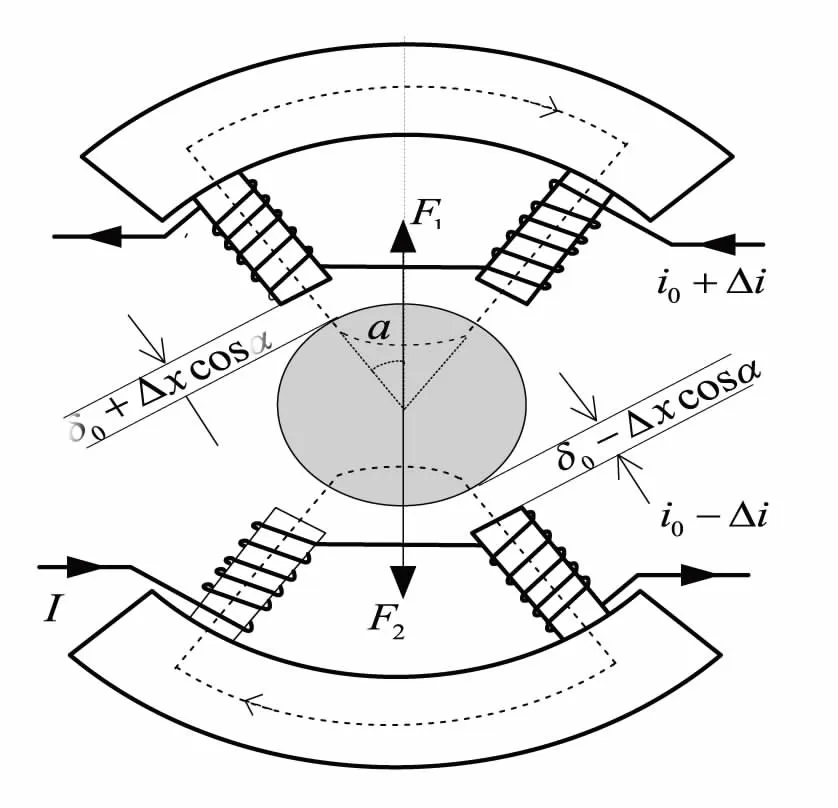
图3 主动磁轴承差动结构

差动控制结构电磁轴承在x方向上的对置C型磁极的等效电磁合力为：

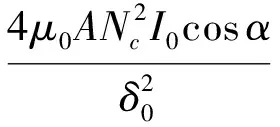
(2)

同理，差动控制结构电磁轴承在y方向上的等效电磁合力为：

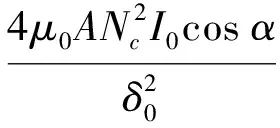
(3)

2.3 等效刚度及等效阻尼

当主动磁轴承采用经典的PID控制器时，则磁轴承控制系统的等效刚度及等效阻尼可表示如下.

若电主轴转子节点ni和nj处各设有一个径向磁轴承，根据式(2)和式(3)，则主动磁轴承的电磁控制力矩阵为：

(4)

而ni和nj分别在x和y方向的PID控制器可写成如下表达式：

(5)

由式(4)和式(5)整理可得式(6).

(6)

式中，Keq和Deq分别为磁轴承控制系统的等效刚度和等效阻尼：

2.4 动态切削力模型

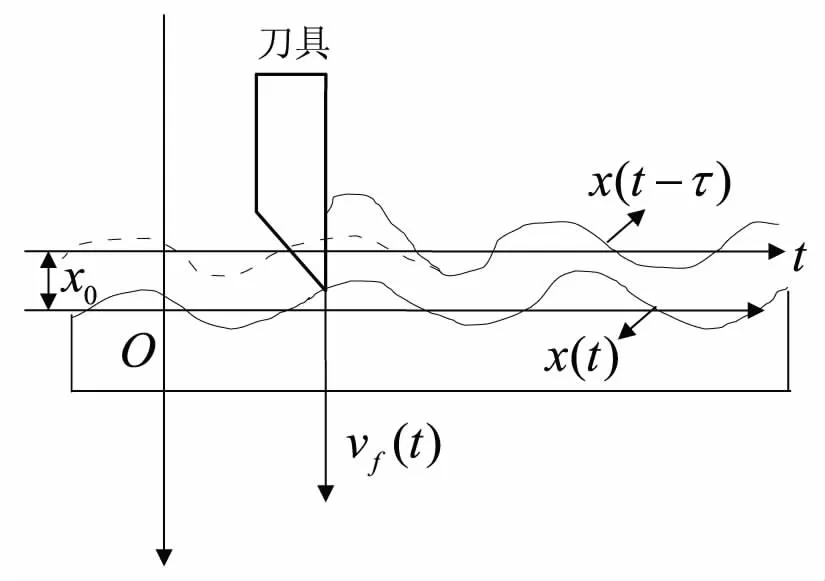
图4 动态切削过程

机床在切削过程中产生振动，导致切削力不断变化，动态切削过程如图4所示[11].x方向上的动态切削力可表示为：

ΔFcu,x(t)=

Kcb[-x(t)+x(t-τ)]-DtΔvf(t)=

(7)

其中x(t),x(t-τ)分别是本次和上一次振动幅值；τ是两次相邻切削之间的延时时间，b是切削宽度，Kc是切削厚度方向上的静态切削力系数，Dt为切削阻尼，vf是进给速度，方向见图4.

以该切削过程x方向上的振动为研究对象，根据式(1)、式(6)和式(7)，可得主动磁轴承动态切削整理后的运动方程为：

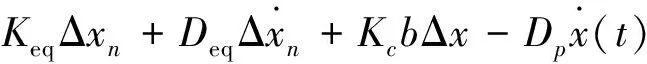
(8)

式中:Δx=[-x(t)+x(t-τ)];Dsep为综合了主动磁轴承切削阻尼后的阻尼矩阵;Kse为综合了主动磁轴承等效刚度后的刚度矩阵.

3 主动磁轴承支承及切削的刚度对柔性电主轴转子动态特性的影响

本文利用matlab开发的有限元软件，在动态切削下对由主动磁轴承支承的柔性电主轴转子系统的动态特性进行了研究，研究所用电主轴参数为：电主轴质量为m=9.6 kg，电主轴长度l=720 mm，铁心长度le=200 mm，转子外径Dr,out=100 mm，转子内径Dr,in=50 mm.

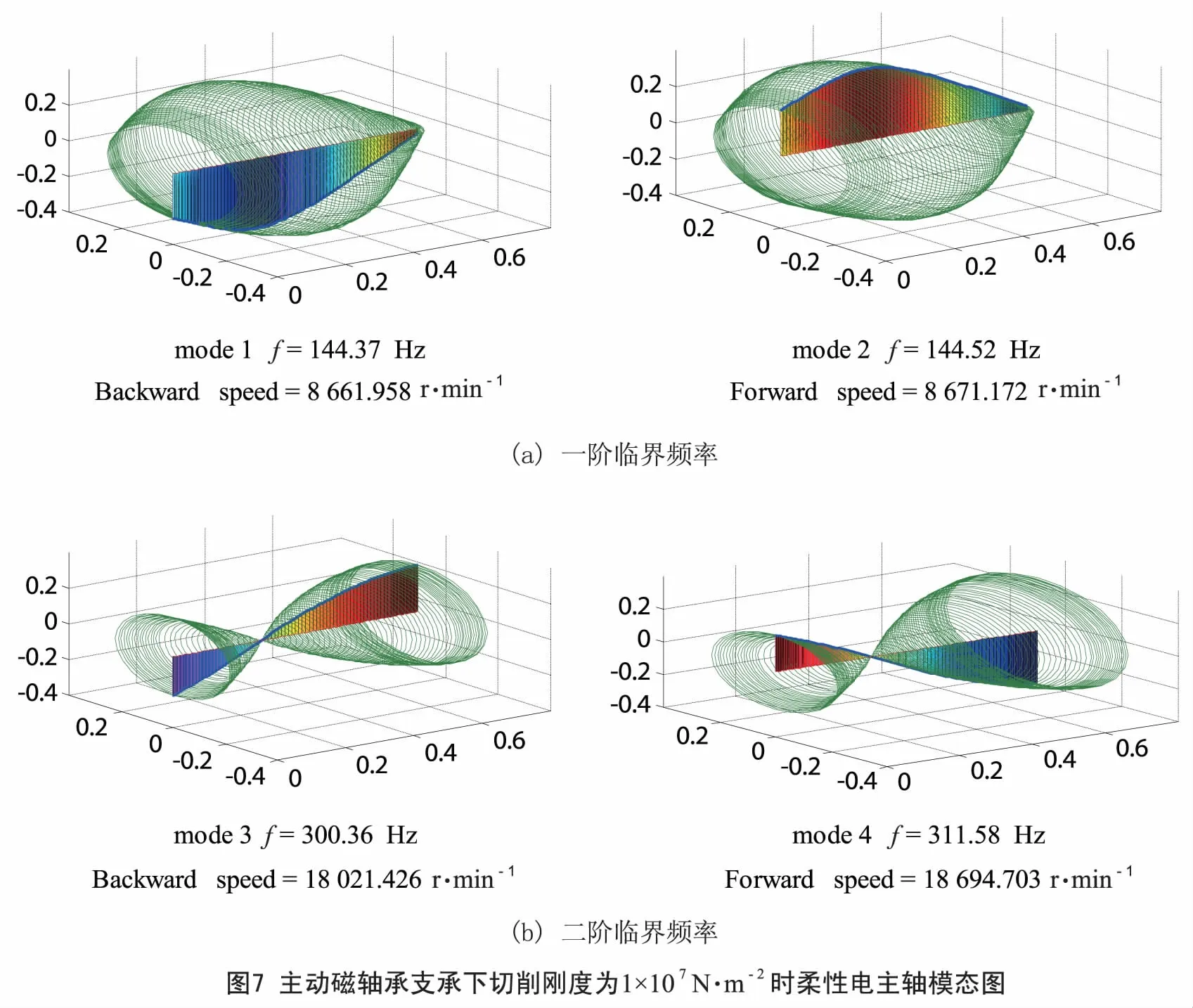
在分析主动磁轴承等效刚度及切削力系数对柔性电主轴转子的动态影响前，首先给出刚性轴承下柔性电主轴的动态特性图，如图5所示.该电主轴的前二阶正向和反向涡动临界频率分别为：206.70 Hz,208.70 Hz,410.54 Hz,417.35 Hz.若换为主动磁轴承，当主动磁轴承的等效刚度为Keq=1×107N·m-2、等效阻尼设为零时，由图6可知，该电主轴的前二阶正向和反向涡动临界频率分别将为：136.43 Hz,137.02 Hz,151.71 Hz,153.13 Hz.在此主动磁轴承等效刚度下，图7给出了切削力系数为Kc=1×107N·m-2时电主轴的特性图，可看出此时电主轴的前二阶正向和反向涡动临界频率分别为：144.37 Hz,144.52 Hz,300.16 Hz,311.58 Hz.由以上分析可知，主动磁轴承的等效刚度将较大幅度地影响柔性电主轴的各阶临界频率，切削力系数的变化也会改变柔性电主轴的各阶临界频率.

4 主动磁轴承及切削力参数对切削动态特性的影响

机床在切削过程中刀具处的频率响应将直接决定着切削过程的稳定性，从而决定切削工件的表面质量.因此，分析主动磁轴承的等效刚度和阻尼、所切削工件的材料(切削力系数)及切削的阻尼对刀具处频率响应的影响等，将具有重要的意义.

4.1 等效刚度的影响

图8分析了主动磁轴承不同的等效刚度(Keq=5×106N·m-2,Keq=1×107N·m-2,Keq=5×107N·m-2)对刀具端频率响应的影响.图8表明，随着主动磁轴等效刚度的增大，刀具端频率响应的最大负实部所对应的频率也逐渐增大，负实部的值却随之减小，这表明磁轴承等效刚度的增大，将增大切削过程稳定区域的临界频率及稳定区域.

4.2 主动磁轴承阻尼的影响

在主动磁轴承刚度Keq=5×107N·m-2时，图9分析了不同的主动磁轴承阻尼(Deq=5×103N·s·m-1,Deq=1×104N·s·m-1)对刀具端频率响应的影响.从图9可以看出，主动磁轴承的等效阻尼将影响刀具端频率响应负实部的大小，随着阻尼的增大，负实部的绝对值随之减小；而对其临界频率却无影响.

4.3 切削阻尼的影响

在主动磁轴承等效刚度Keq=5×107N·m-2、等效阻尼Deq=1×103N·s·m-1时,图10分析了不同的切削阻尼(Dt=100 N·s·m-1,Dt=500 N·s·m-1)对刀具端频率响应的影响.图10表明，不同的切削阻尼对刀具端频率响应的影响，与主动磁轴承的等效阻尼影响规律相同，但影响力度较大.

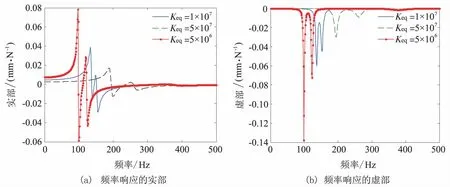
图8 不同主动磁轴承刚度下刀具端频率响应

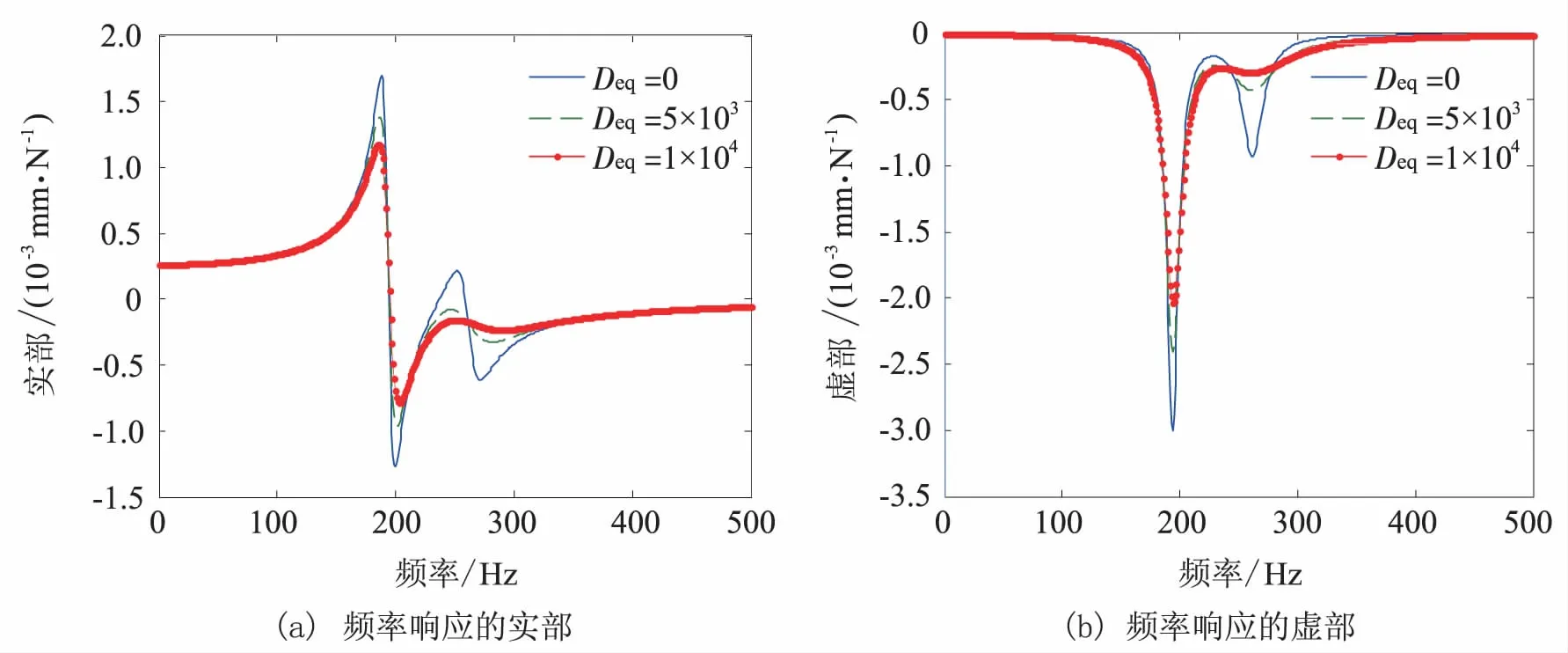
图9 不同主动磁轴承阻尼下刀具端频率响应

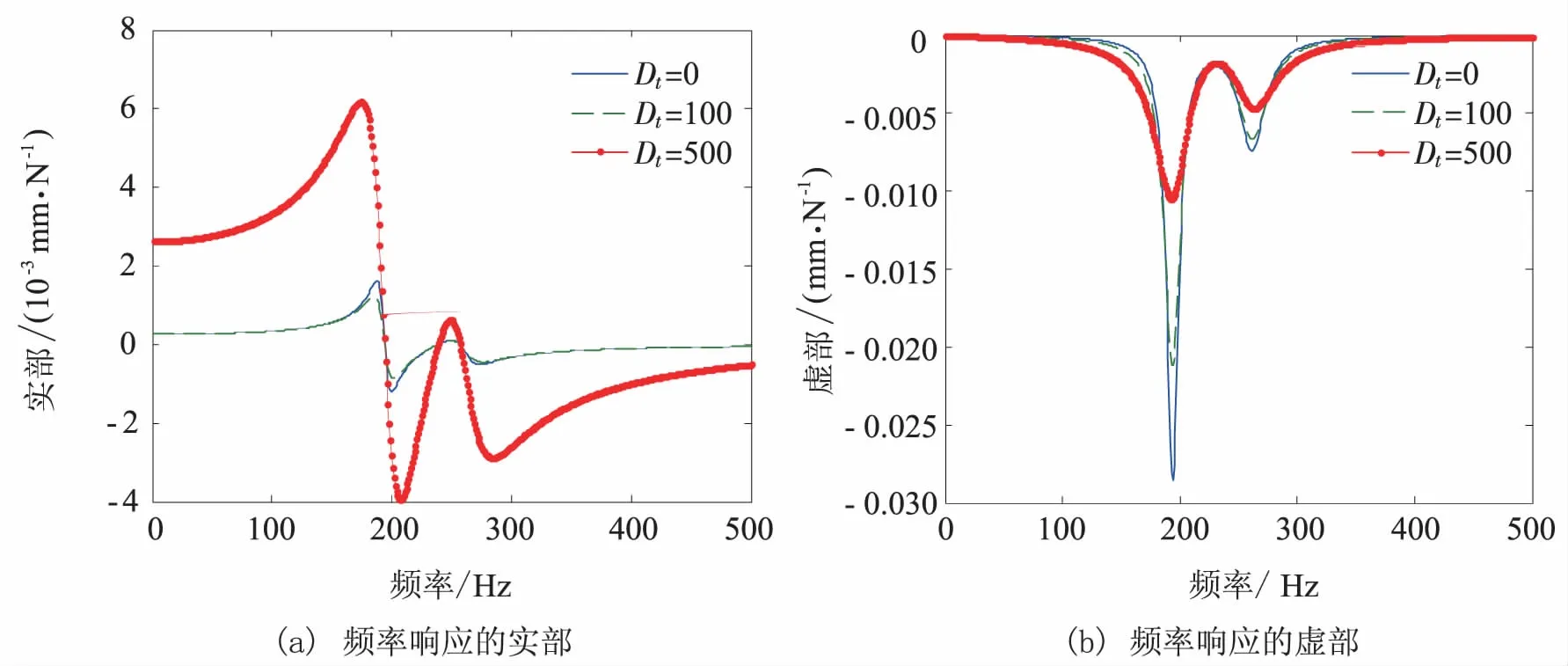
图10 不同切削阻尼下刀具端频率响应

5 主动磁轴承及切削阻尼对切削稳定性的影响

系统的动态响应是反映主动磁轴承切削系统稳定性的前提，令主动磁轴承柔性电主轴切削系统的频率响应为：

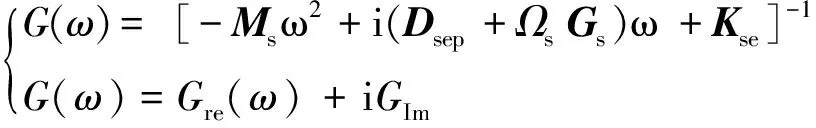
(9)

则求解式(9)得

G(ω)[kcb[-x(t)+x(t-τ)]⟹

(10)

要使切削系统稳定，则必须满足

(11)

对式(10)两边平方并整理得

(12)

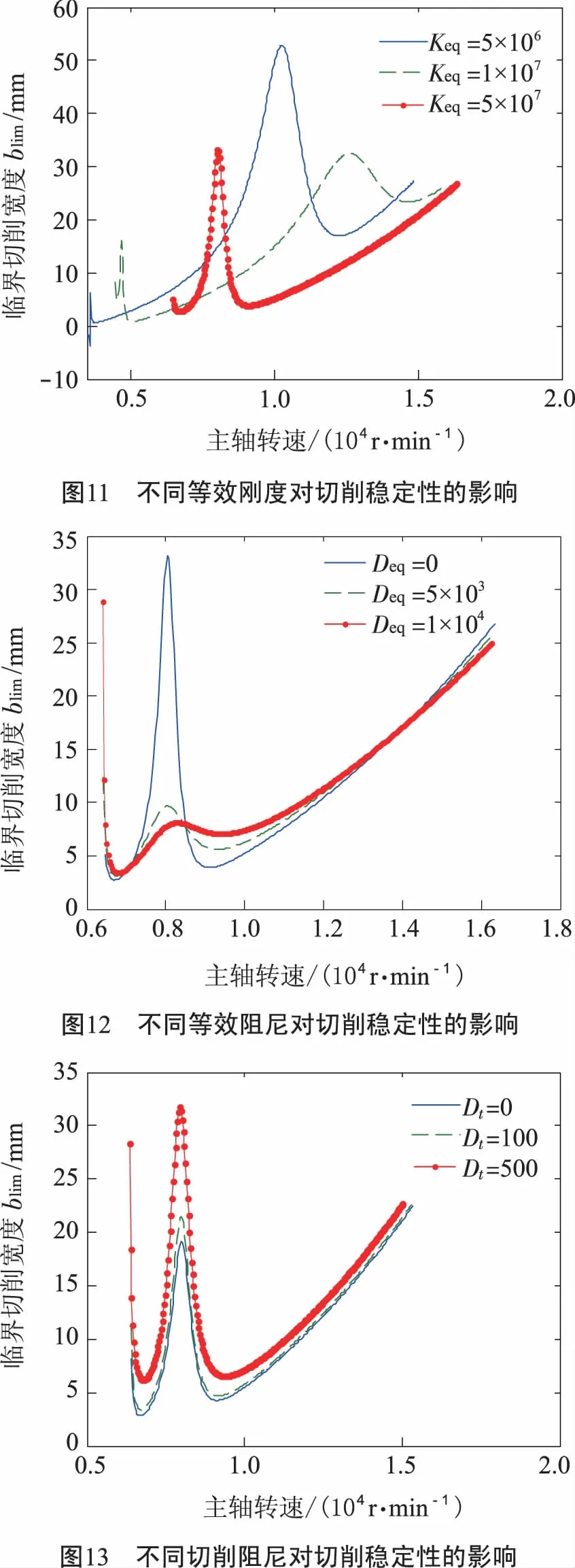
主动磁轴承不同的等效刚度、等效阻尼及切削阻尼对切削稳定性的影响，如图11至图13所示.

图11表明，随着主动磁轴承等效刚度的增大，切削的稳定性区域向右移动，即切削的临界转速升高，这与图8相吻合，但稳定性区域减小.

图12表明，随着主动磁轴承等效阻尼的增加，最小切削宽度增加，稳定性区域增大，这也与图9的主动磁轴承等效刚度对刀具端频率响应的影响一致.

在主动磁轴承等效刚度Keq=5×107N·m-2、等效阻尼Deq=103N·s·m-1时,图13分析了不同的切削阻尼(Dt=100 N·s·m-1,Dt=500 N·s·m-1)对切削稳定性的影响.图13表明，切削阻尼能够增大切削的最小临界宽度，提高切削的稳定性区域，而不改变切削的临界转速.

6 结论

本文以主动磁轴承支撑的柔性电主轴转子为研究对象，分析了主动磁轴承不同的等效刚度及切削力系数对电主轴模态及临界转速的影响，考虑了主动磁轴承等效刚度和阻尼对刀具端频率响应的影响，进而讨论了主动磁轴承不同的等效刚度、等效阻尼及切削阻尼对切削稳定性的影响.分析结果表明，主动磁轴承等效刚度对电主轴的模态频率影响较大；而对刀具端的频率响应分析可知，随着主动磁轴承等效刚度的增大，将增大频率响应的最大负实部及虚部的位置和其最大值；主动磁轴承的等效阻尼和切削阻尼仅影响刀具端频率响应大的最大负实部及负虚部的值，且切削阻尼的影响较大；刀具端的频率响应同样也反映了切削的稳定性，这在图11、图12和图13中得到了验证.

[1]ZHANG L L,QIN X Y. Dynamic analysis of electric spindle based on ANSYS [J].Applied Mechanics and materials,2013,288:75-79.

[2]WANG M, ZHANG X Y,ZAN T, et al. Investigation of static and dynamic characteristics of a high-speed electric spindle based on ANSYS[J]. Journal of Beijing Unversity of Technology,2012,38(7):987-991.

[3]XIE Z Y, YU K, WEN L T, et al. Characteristics of motorized spindle supported by active magnetic bearings[J].Chinese journal of Aeronautics,2014,27(6):1619-1624.

[4]XU X, XIE Z Y, LONG Y W. Dynamic characteristics of low loss motorized spindle suspended by magnetic bearings[J].Journal of Aerospace Power,2014,29(2):343-349.

[5]BOUAZIZ A, BOUAZIZ S, HENTATI T, et al. Vibrations monitoring of high speed spindle with active magnetic bearings in presence of defects[J]. International Journal of Applied Electromagnetics & Mechanics,2015,49(2):207-221.

[6]BOUAZIZ A, BARKALLAH M, BOUAZIZ S, et al. Cutting parameters and vibrations analysis of magnetic bearing spindle in milling process[J]. Journal of Theoretical & Applied Mechanics,2016,54(3):691.

[7]HUANG T,CHEN Z Y,ZHANG H T, et al. Active control of an active magnetic bearings supported spindle for chatter suppression in milling process[J].Journal of Dynamic Systems, Measurement and control,Transactions of the ASME,2015，11(137):345-356.

[8]BARKALLAH M, BOUAZIZ A, BOUAZIZ S, et al. Modeling and Analysis of Spindle with Active Magnetic Bearings for High-Speed Milling Process[J]. Journal of Mechanics, 2016,32(2):131-141.

[9]乔晓利,祝长生.基于内置力执行器的电主轴铣削颤振的主动控制[J].机械工程学报,2012,1(48):187-192.

[10]蒋科坚.主动电磁轴承——转子系统振动控制技术[D].杭州：浙江大学,2011.

[11]杨橚,唐恒龄,廖伯瑜.机床动力学[M].北京：机械工业出版社,1983:25-98.