The Mod 2 Kauffman Bracket Skein Module of Thickened Torus

YAN XIN-MINGAND SUN MENG

(1.Department of Mathematics,Guangdong University of Education,Guangzhou,510303)

(2.The China-Russian Joint Training Graduate School,Heilongjiang University,Harbin,150080)

Communicated by Lei Feng-chun

1 Introduction

We are concerned with framed links in thickened torusT2×Iby using skein theory.We will extend the Kauffman bracket skein module to the mod 2 Kauffman bracket skein module and obtain an expression of a framed link as a new ambient isotopic invariant.

Skein relations have their origin in an observation by Alexander[1],Conway found a way to calculate the Alexander polynomial of a link using a so-called skein relation[2].This is an equation that relates the polynomial of a link to the polynomial of links obtained by changing the crossings in a projection of the original link.Skein modules were introduced by Przytycki in[3].Skein modules are quotients of free modules over ambient isotopy classes of framed links in a 3-manifold by properly chosen local skein relations.The skein module based on Kauffman bracket skein relation is one of the most extensively studied object of the algebraic topology based on framed links,which is also an important invariant of 3-manifolds.There have been extensive study and application of Kauffman bracket skeinmodule(see[4]–[8]).

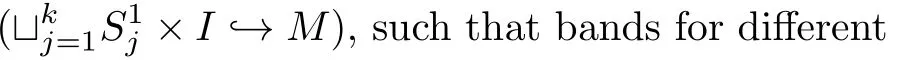
If we work with regular projections of links,then the topology of links is reflected by Reidemeister moves.Regular isotopy is the equivalent relation on link projections generated by the Reidemeister moves of types II and III.The Reidemeister moves of types II and III on the cores of bands extend to the bands themselves,while the type I move dose not extend(it corresponds to a full twist on the band).Consequently,regular isotopy corresponds to ambient isotopy of framed links.

Noted that torus knot is a kind of knot that had been investigated and used widely(see[9]).We are concerned in this paper with the torus knot,which is defined below.Given two generatorsx1,x2inπ1(T2),where

and consider the closed curve

If(p,q)=(0,0)orp,qare relatively prime,thenγis called a(p,q)knot inT2,denoted byK(p,q).Obviously,

This paper is organized by two sections:In Section 2,we cover the necessary definitions and lemmas.The main result and its proof are provided in Section 3.

2 Preliminary

The data that determine a knot in R3are usually given by a projection onto a plane.Now we derive it in thickened surfaceF×Ias inR3.

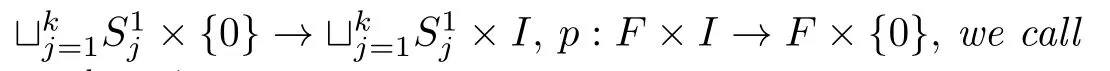
Definition 2.2[10]A projection ℓ of a framed link L is called regular if

(1)ℓ is an immerse;

(2)there are only finitely many intersections in ℓ and all intersections are double points;

(3)ℓ is transverse to the every intersection point.

Moreover,if the upper crossing line and the lower crossing line are marked at every double point in a regular projection,then this regular projection of a link is called a link projection.

We work always in the smooth-category.We do not make any distinction between two ambient isotopic framed links,while two framed links,LandL′,inMare said to be ambient isotopic if there is a smooth orientation preserving automorphismh:M→Msuch thath(L)=L′.

Then we give the definition of the Kauffman bracket skein module ofF×Ifor an oriented surfaceFand an intervalIas follows:

Definition 2.3[3],[11]The Kauffman bracket skein module of3-manifold F×I,S2,∞(F×I;R,A)is defined as follows:Let L be the set of unoriented framed links in F×I(including the empty knot Ø),R any commutative ring with identity and A an invertible element in R.Let RL be the free R-module generated by L,S2,∞be the submodule of RL generated by two skein expressions:L+−AL0−A−1L∞,L⊔T1+(A2+A−2)L,where the triple L+,L0and L∞as presented by their regular projections ℓ+,ℓ0and ℓ∞on F are shown in Fig.2.1,which can be ambient isotopy except within the neighborhood shown,and T1denotes the trivial framed knot.Set S2,∞(F×I;R,A)=RL/S2,∞.The notation is shortened for special case:

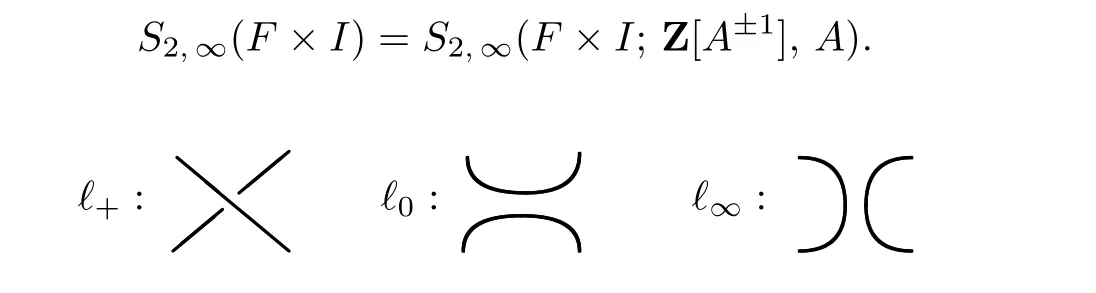
Fig.2.1 Link projections

From the above definition,we have:

Proposition 2.1For a framed link L in F×I,its expression in S2,∞(F×I)is an ambient isotopic invariant of L.

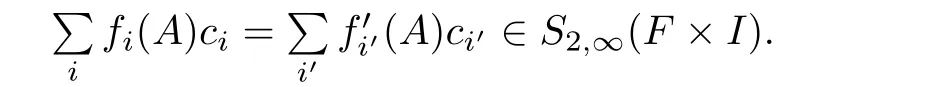
Moreover,the expression ofLin the free module is unique.Hence,it is an ambient isotopic invariant of the framed linkL.

The following lemmas are used later.

Lemma 2.1[8]S2,∞(F×I;R,A)is a free R-module with a basis B(F)consisting of links in F without contractible components(but including the empty knot).

Lemma 2.2[9]Suppose that K(p,q)and K(p′,q′)are two knots in T2.If K(p,q)∩K(p′,q′)=Ø,then K(p,q)=K(p′,q′)or one of them is K(0,0).

3 Main Results

Beginning with our main ingredient,we consider the special caseT2×I.GivenS2,∞(T2×I;R,A)the Kauffman bracket skein module ofT2×Iand

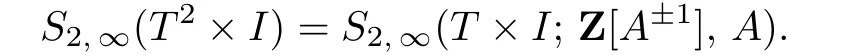
For a framed linkLinT2×I,by Lemma 2.1,its expression in the free moduleS2,∞(T2×I)is presented as

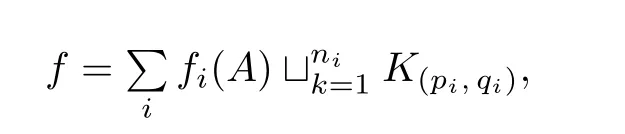
whereK(pi,qi)is a(pi,qi)knotinT2.

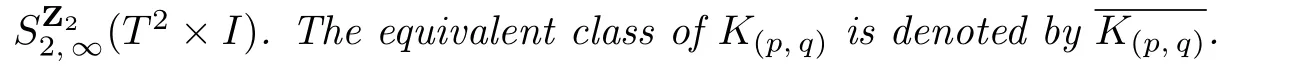
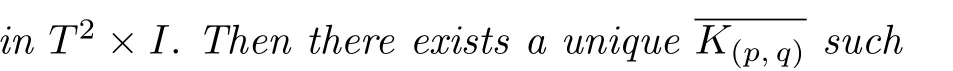
Proof.Suppose thatLis a framed link inT2×Iwith framing(ϕ1,···,ϕk).By skein expression,we have

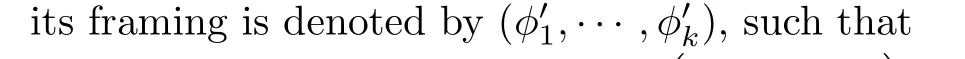
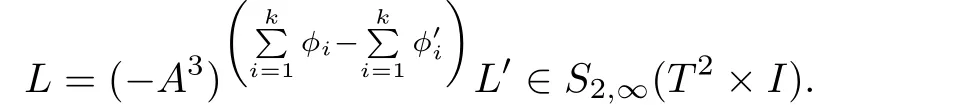
By the first skein expression of Definition 2.3,we also have

it is followed that

whereSdenotes one of the states ofℓ;

obviously,a(S)+b(S)=V(ℓ);LSdenotes the framed link without crossing in the stateS,including contractible components.In fact,LSis a union of some(p,q)knots inT2.

Nextly,by the second skein expression of Definition 2.3,we see

wherem(S)denotes the number of contractible components,andn(S)denotes the number of uncontractible components.

From the above analysis we obtain

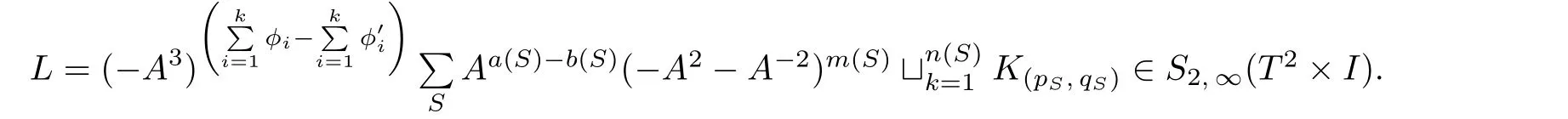
By Lemma 2.1,the expression ofLis unique after collecting the link terms.

Without loss of generality we assume that

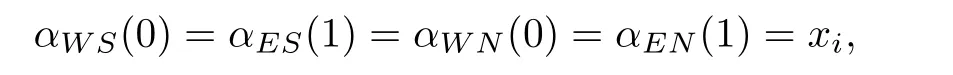
which decides the direction of four paths as shown in Fig.3.1.

Fig.3.1 The directions of four paths

We are now in a position to discuss the following three cases:

Case 1.Provided thatαWS(1)=αES(0),αWN(1)=αEN(0),we have

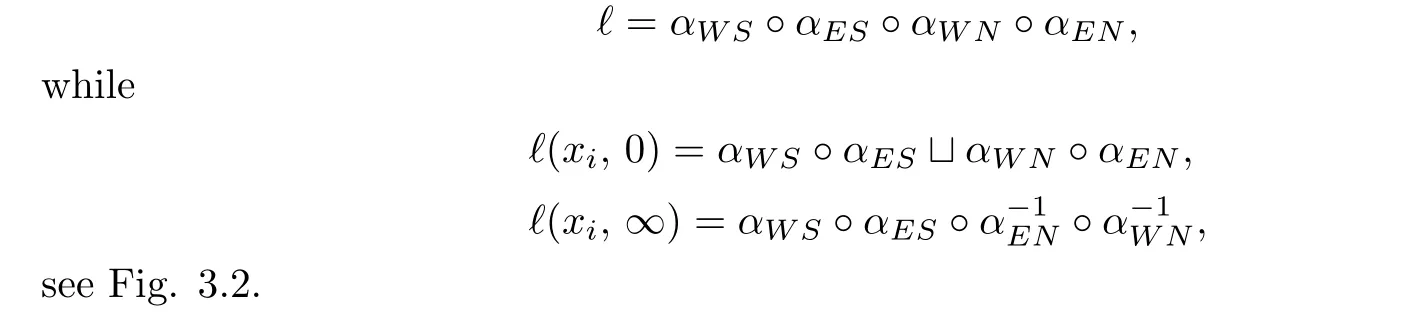
Fig.3.2 The link projections for Case 1

Notice that inℓ(xi,0),αWN◦αEN∩αWS◦αES=Ø.Using Lemma 2.2,we can now deriveαWN◦αEN=αWS◦αESor one ofαWN◦αEN,αWS◦αESisK(0,0).The results of these calculations are given in Table 3.1.

It should be noted that the subtraction here is a formal subtraction,and the result of each subtraction is obtained by the analysis of actualℓ(xi,0)andℓ(xi,∞).Besides,for unoriented(p,q)knot,K(p,q)=K(−p,−q).

Table 3.1 The results for Case 1

It follows from Table 3.1 that there exists a uniqueK(p,q)∈π1(T2),such that

Case 2.Provided thatαWS(1)=αEN(0),αWN(1)=αES(0),we have

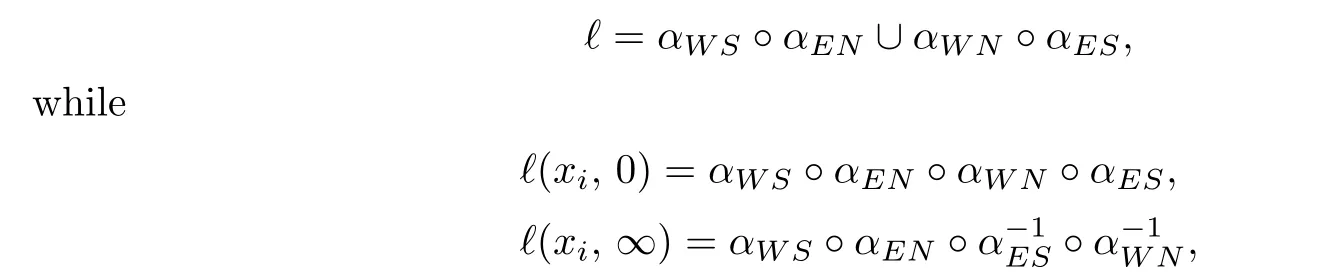
see Fig.3.3.

Fig.3.3 The link projections for Case 2

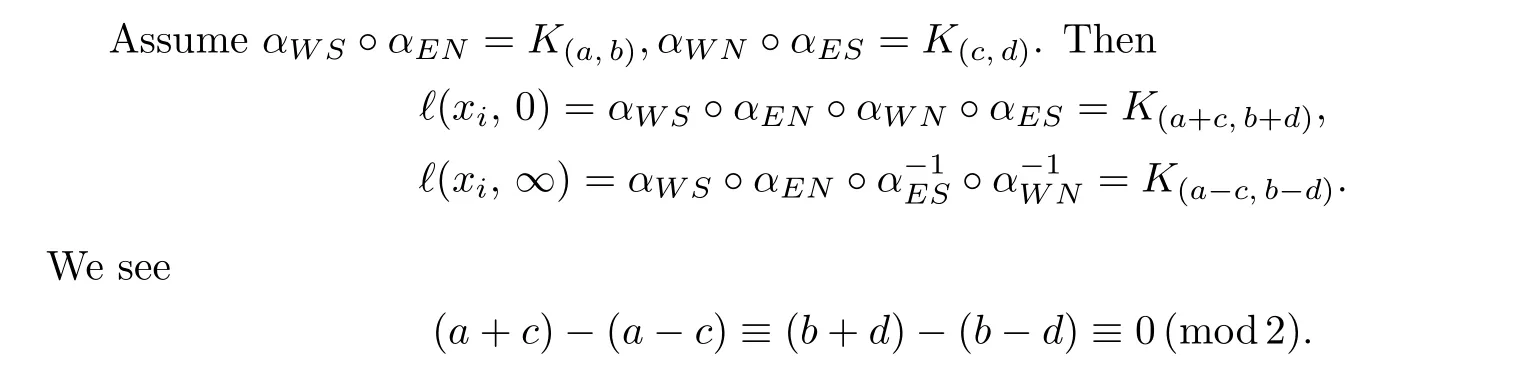
Case 3.Provided thatαWS(1)=αWN(1),αEN(0)=αES(0),we have

Fig.3.4 The link projections for Case 3

By Lemma 2.2,we also have the results in the Table 3.2.

Table 3.2 The results for Case 3

It follows from Table 3.2 that there exists a uniqueK(p,q)∈π1(T2),such that

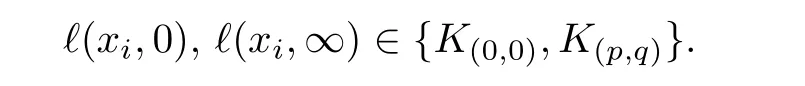
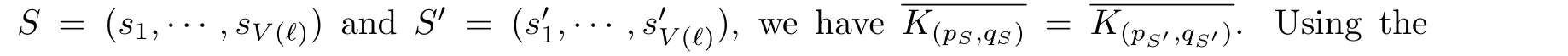
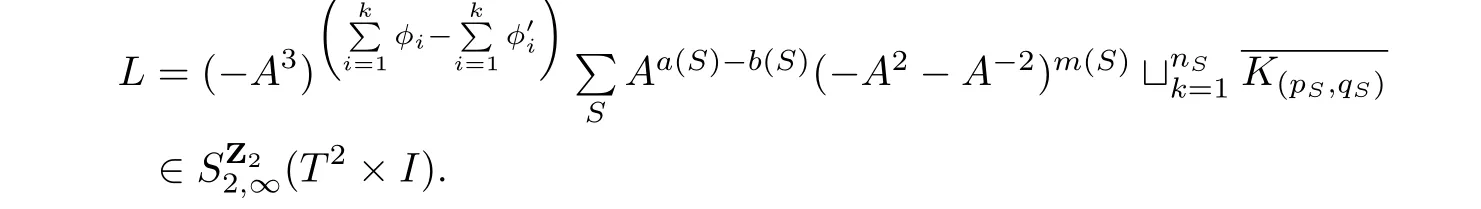
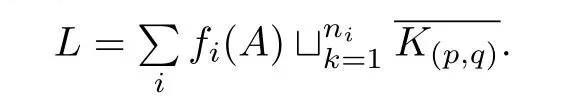
being an ambient isotopic invariant ofLby Proposition 2.1.

We complete the proof.

[1]Alexander J W.Topological invariants of knots and links.Trans.Amer.Math.Soc.,1928,30(2):275–306.

[2]Conway J H.An enumeration of knots and links,and some of their algebraic properties.in:1970 Computational Problems in Abstract Algebra Proc.Conf.,Oxford:Pergamon,1967,pp.329–358.

[3]Przytycki J H.Skein modules of 3-manifolds.Bull.Polish.Acad.Sci.Math.,1991,39(1-2):91–100.

[4]Bullock D,Przytycki J H.Multiplicative structure of Kauffman bracket skein module quantizations.Proc.Amer.Math.Soc.,2000,128(3):923–931.

[5]Bullock D.A finite set of generators for the Kauffman bracket skein algebra.Math.Z.,1999,231:91–101.

[6]Bullock D.Rings of SL2(C)-characters and the Kauffman bracket skein module.Comment.Math.Helv.,1997,72(4):521–542.

[7]Hoste J,Przytycki J H.Homotopy skein modules of orientable 3-manifolds.Math.Proc.Cambridge Philos.Soc.,1990,108(3):475–488.

[8]Przytycki J H.Fundamentals of Kauffman bracket skein modules.Kobe J.Math.1999,16(1):45–66.

[9]Rolfsen D.Knots and Links.in:Mathematics Lecture Series,No.7.Berkeley:Publish or Perish,Inc.,1976:53–55.

[10]Yan X M.Estimating the self-intersection number of closed curves on surface by knot method.Geom.Dedicata,2015,175:65–67.

[11]Hoste J,Przytycki J H.A survey of skein modules of 3-manifolds.in:Knots 90,Proceedings of International Conference on Knot Theory and Related Topics,Osaka(Japan),August 15–19,1990,(ed.Kawauchi A.),Berlin:Walter de Gruyter,1992:363–379.