On Lie 2-bialgebras

QIAO YU AND ZHAO JIA

(School of Mathematics and Information Science,Shaanxi Normal University,Xi’an,710119)

Communicated by Du Xian-kun

1 Introduction

1.1 Background

This paper is a sequel to[1],in which the notion of Lie 2-bialgeras was introduced.The main purpose of this paper is to give an equivalent condition for Lie 2-bialgebras.Generally speaking,a Lie 2-bialgebra is a Lie 2-algebra endowed with a Lie 2-coalgebra structure,satisfying certain compatibility conditions.As we all know,a Lie bialgebra structure on a Lie algebra(g,[·,·])consists of a cobracketδ:g→g∧g,which squares to zero,and satisfies the compatibility condition:for allx,y,z∈g,

Consequently,one may ask what is a Lie 2-bialgebra.A Lie 2-bialgebra is a pair of 2-terms ofL∞-algebra structure underlying a 2-vector space and its dual.The compatibility conditions are described by big bracket(see[1]).And anL∞-algebra structure on a Z-graded vector space can be found in[2]–[4].This description of Lie 2-bialgebras seems to be elegant,but one cannot get directly the maps twisted between them and compatibility conditions.This is what we will explore in this paper.

This paper is organized as follows:In Section 1,we recall the notion of big bracket,which has a fundamental role in this paper.Then,we introduce the basic concepts in Section 2 which is closely related to our result,that is,Lie 2-algebras and Lie 2-coalgebras,most of which can be found in[3].Finally,in Section 3,we give an equivalent description of Lie 2-bialgebras,whose compatibility conditions are given by big bracket.

1.2 The Big Bracket

We introduce the following Notations.

(1)LetVbe a graded vector space.The degree of a homogeneous vectoreis denoted by|e|.

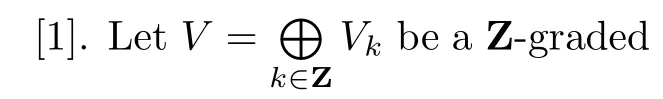
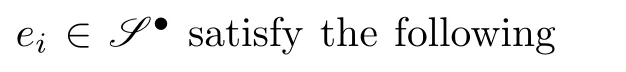
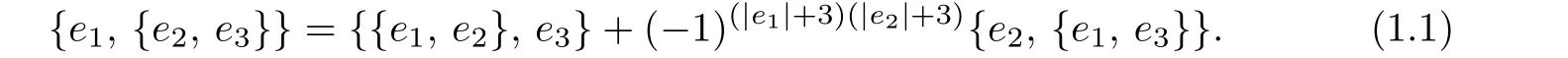
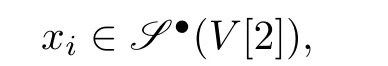
Lemma 1.1The following equations hold:

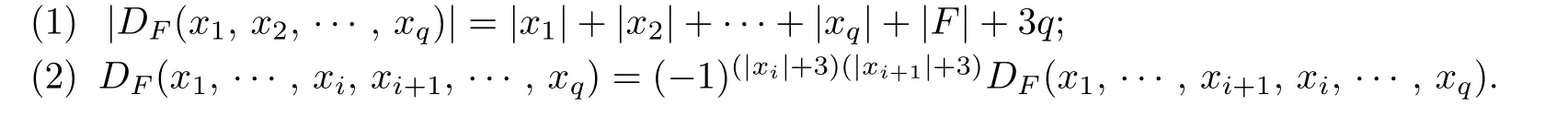
Proof.Since the degree of big bracket is 3,we apply this factq-times to obtain(1).

Ifq=2,by(1.1),we have

It is easy to check that if{x1,{x2,F}}={{F,x2},x1},then

and if{x1,{x2,F}}=−{{F,x2},x1},then

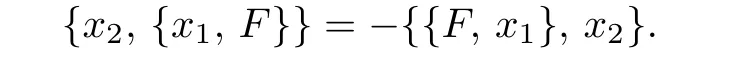
By induction,we conclude the proof.

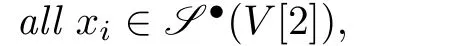
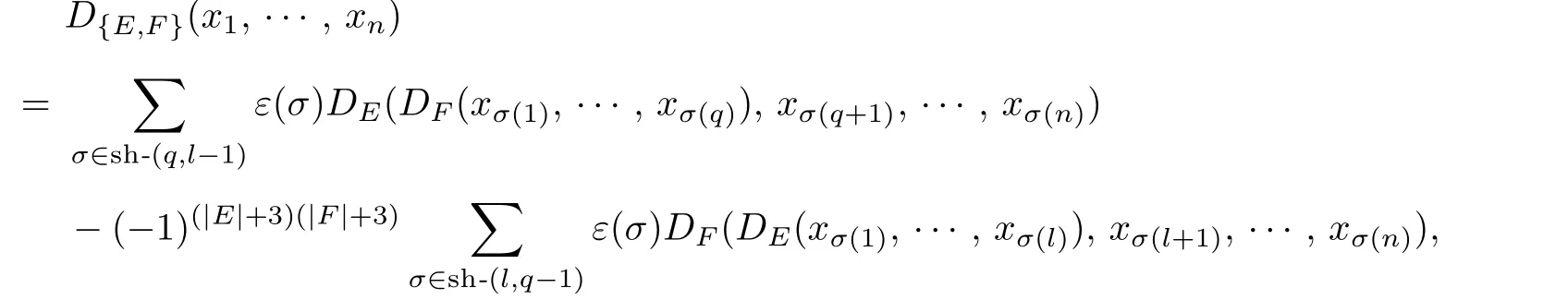
where n=q+l−1,and heresh-(j,n−j)denotes the collection of all(j,n−j)-shuffles,and ε(σ)means that a sign change(−1)(|xi|+3)(|xi+1|+3)happens if the place of two successive elements xi,xi+1are changed.

Proof.Ifn=1,by(1.1),we get that

Ifn≥2,by(1.1)and Lemma 1.1,the result can be derived easily.

2 Lie 2-algebras and Lie 2-coagebras

2.1 Lie 2-algebras

We now pay special attention toL∞-algebra structure restricted to 2-termsV=θ⊕g,whereθis of degree 1,and g is of degree 0,while the shifted vector spaceV[2]andV∗[1]should be considered.One can read[1]and[6]for more details ofL∞-algebras,where the notion ofL∞-algebra is called an SH(strongly homotopy)Lie algebras.And the degrees of elements in g,θ,g∗,andθ∗can be easily obtained by a straight computation(see[1]and[4]).The following concept is taken from[1]and[6]:

Definition 2.1A Lie2-algebra structure on a2-graded vector spacesgand θ consists of the following maps:

(1)a linear map ϕ:θ→g;

(2)a bilinear skew-symmetric map[·,·]:g∧g→g;

(3)a bilinear skew-symmetric map·≻·:g∧θ→θ;

(4)a trilinear skew-symmetric map h:g∧g∧g→θ,

such that the following equations are satisfied:for all x,y,z,w∈g,u,v∈θ,

(c)ϕ(u)≻v+ϕ(v)≻u=0;

(d)ϕ(x≻u)=[x,ϕ(u)];

(e)h([x,y],z,w)+c.p.=−w≻h(x,y,z)+c.p.,wherec.p.stands for cyclic permutation.

In the sequel,we denote a Lie 2-algebra by(θ,g;ϕ,[·,·],·≻·,h)or simply(θ,g).One may be confused with these notions since in[1]the same notions are used to denote the strict Lie 2-algebras,which are different from our weak sense.But in this paper,the notions denote the weak cases without other statements.

We should point out that the notion of Lie 2-algebras stands for different meaning in different literatures.The notion of semidirect Lie 2-algebras is not a special case of our Lie 2-algebras in[2],where Baez and Crans treat semidirect Lie 2-algebras as a 2-vector space endowed with a skew-symmetric bilinear map satisfying the Jacobi identity up to a completely antisymmetric trilinear map called Jacobiator,which also makes sense in terms of its Jacobiator identity.By contract our definition of Lie 2-algebras is that of 2-termL∞-algebra in[1]and[6].The reader should distinguish these concepts.However,Baez and Crans[2]have given a one-to-one correspondence between the notion of Lie 2-algebras and 2-termL∞-algebra.

Before we prove a proposition,we give the following lemma.

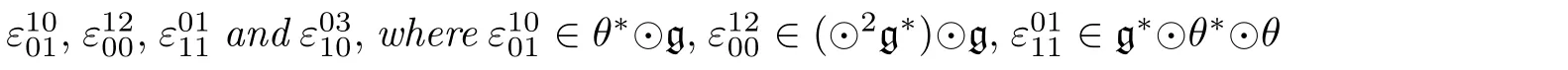
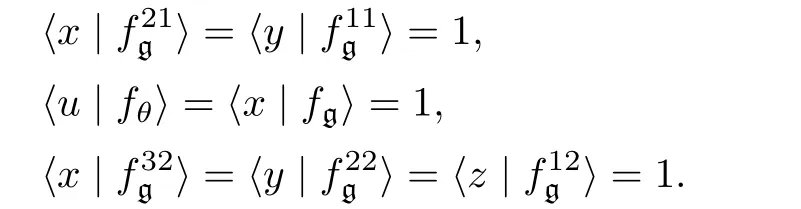
By the language of big bracket,a Lie 2-algebra can be described in a beautiful manner:

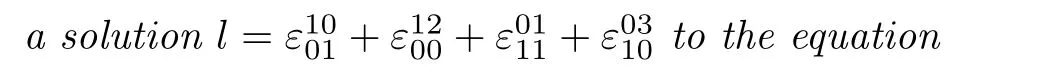
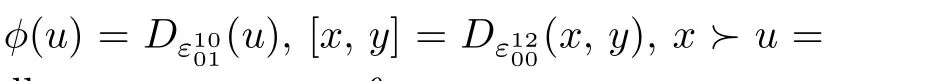
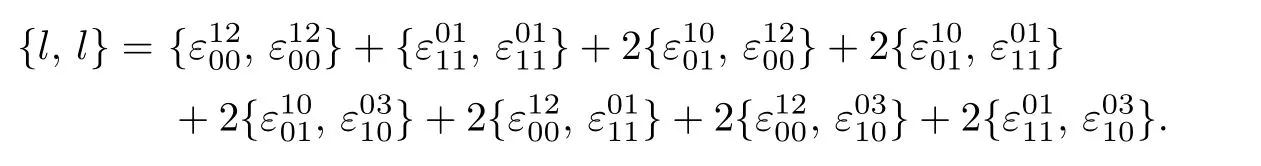
By Lemma 1.2,we have

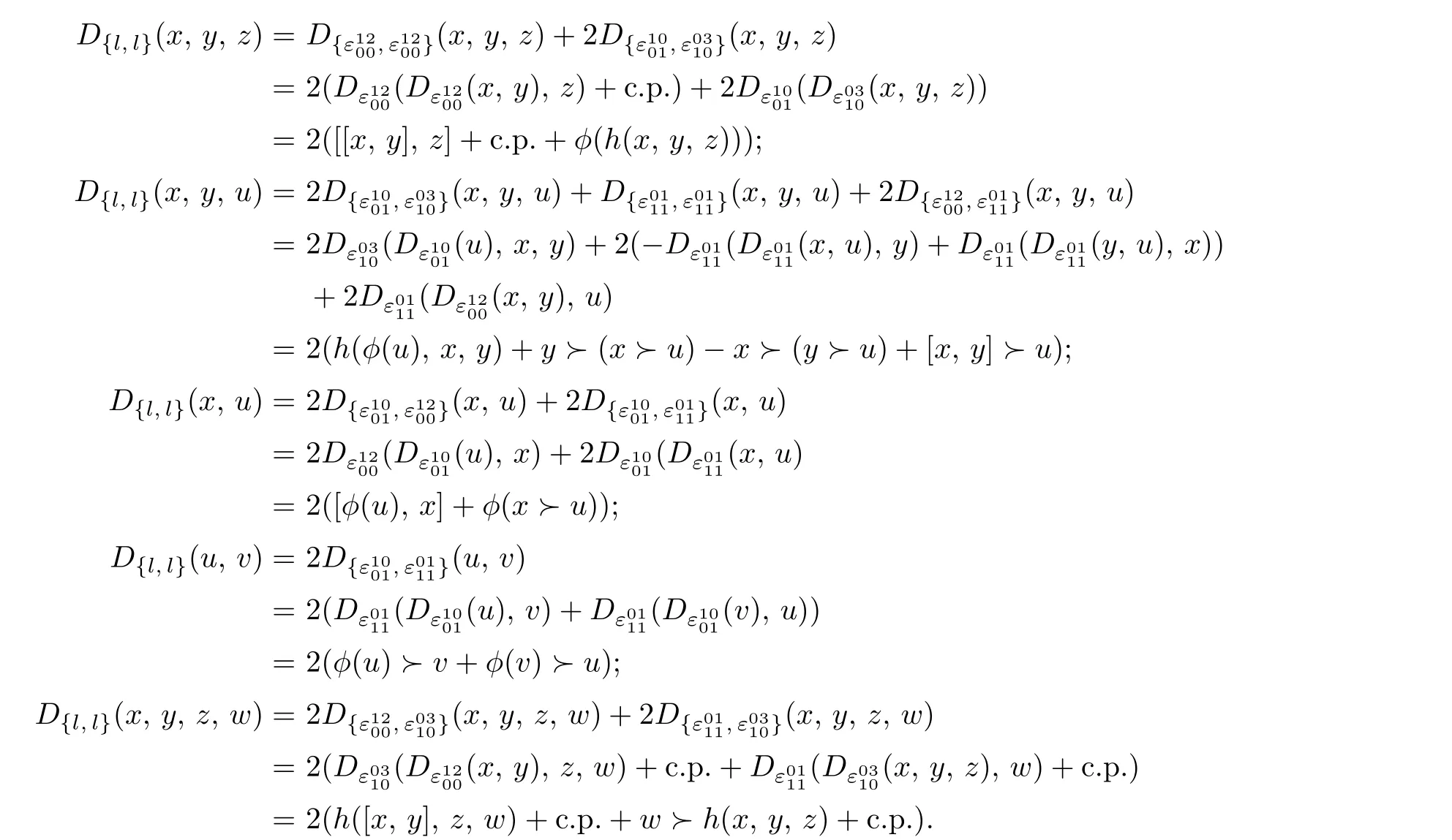
Hence,{l,l}=0 if and only if the right hand side of these equations vanish,which implies that(θ,g)is a Lie 2-algebra.

Remark 2.1Note that in[1],a strict Lie 2-algebra is equivalent to a Lie algebra crossed module.Similarly,one may ask what is a Lie 2-algebra crossed module,this work has been solved in[8].The reader can read this for more details.

Example 2.1LetV3be a 3-dimensional vector space.Then we can construct a Lie 2-algebra as follows:

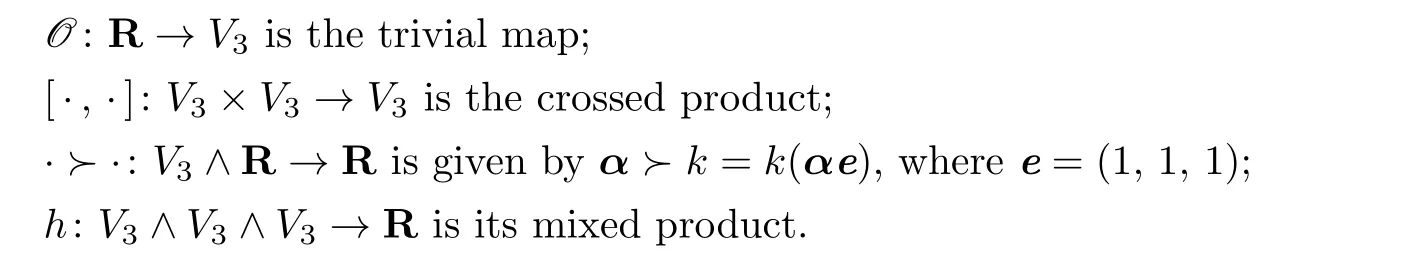
One can easily check thatR⊕V3becomes a Lie 2-algebra.

2.2 Lie 2-coalgebras

As we all know,if(g∗,[·,·]∗)is a Lie algebra,then(g,δ)is a Lie coalgebra,where〈x|[ξ,ς]∗〉=−〈δ(x)|ξ∧ς〉for allx∈g,ξ,ς∈g∗.Similar to the relation between Lie algebras and Lie coalgebras,if(g∗,θ∗)is a Lie 2-algebra,then we call(θ,g)a Lie 2-coalgebra.Besides,we have the following:

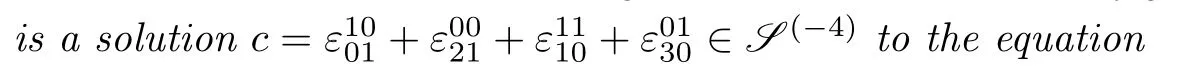
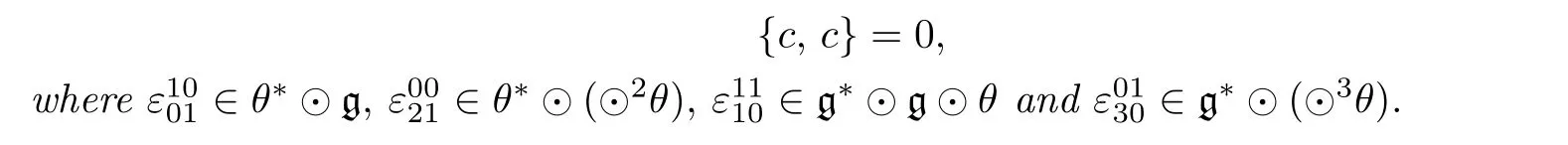
We would give an equivalent condition of a Lie 2-coalgebra by the language of maps and compatibility conditions.The following notations are taken from[1]:

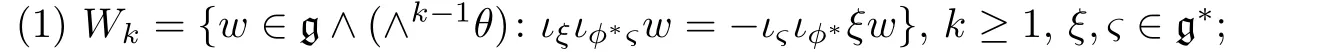
(2)The bilinear map:for allx∈g,u∈θ,

is a degree-0 derivation with respect to the wedge product.

The maps and compatibility conditions of a Lie 2-coalgebra can be summarized as follows.

Theorem 2.1A Lie2-coalgebra structure on(θ,g)is equivalent to the following linear maps δ:g→W2⊂g∧θ,ω:θ→θ∧θ,and η:g→θ∧θ∧θ such that

Proof.According to Proposition 2.1,a Lie 2-coalgebra structure on(θ,g)is equivalent to the fact that(g∗,θ∗)is a Lie 2-algebra,which consists of the following linear maps:

such that for allξ,ς∈g∗,κ,κ1,κ2,κ3,κ4∈θ∗,

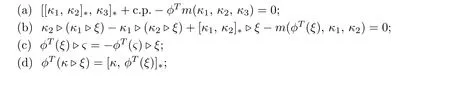
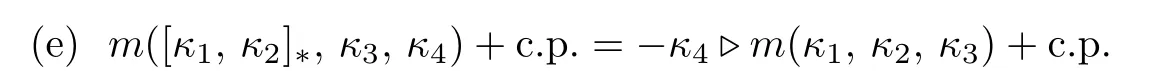
Then a triple of linear maps(δ,ω,η)is defined by:for allx∈g,u∈θ,ξ,ς∈g∗,κ,κ1,κ2,κ3∈θ∗,

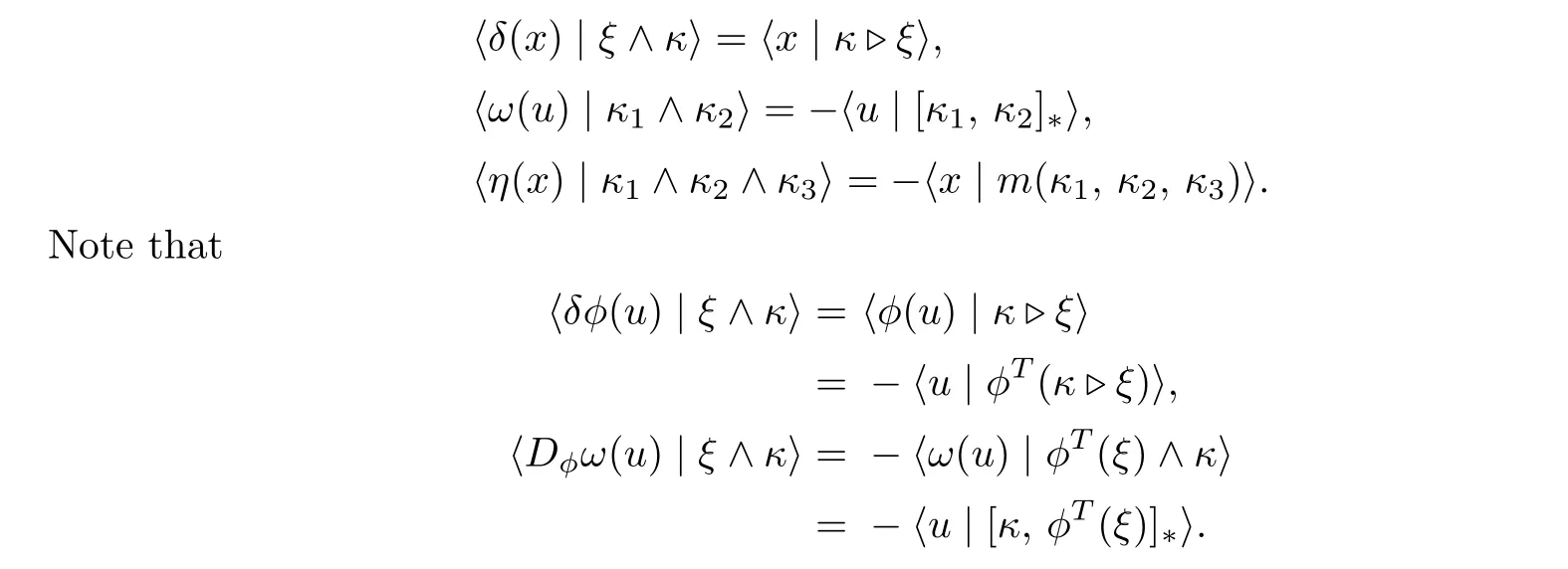
So,Dϕω=δϕis equivalent to(d).

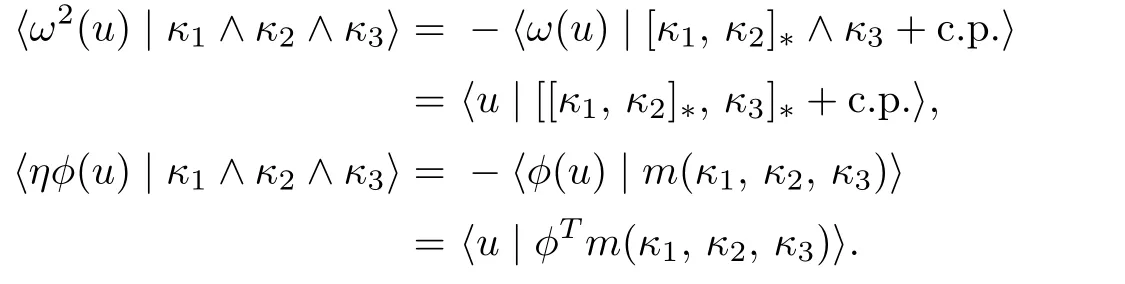
Hence,ω2=ηϕis equivalent to(a).

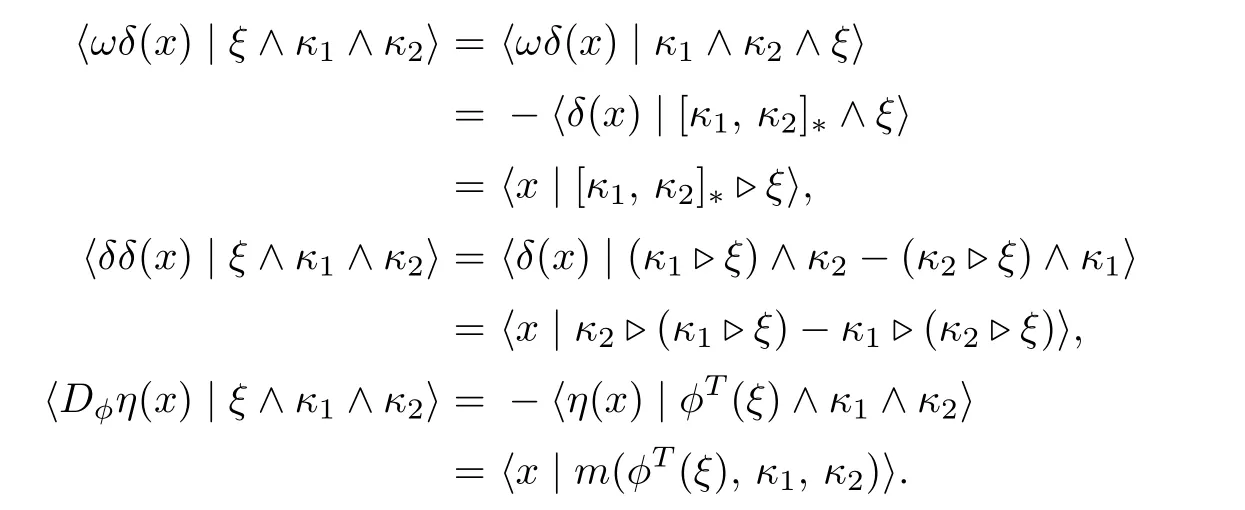
Therefore,(ω+δ)δ=Dϕηif and only if(b)holds.

Thus,ωη=ηδif and only if(e)holds.

Meanwhile,sinceιξιϕ∗ςw=(ξ∧ϕ∗(ς))w,we have thatδ(x)∈W2if and only if(c)holds.

3 Lie 2-bialgebras

3.1 Basic Concepts

The following concept is taken from[1].

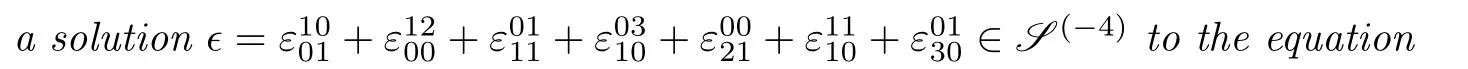
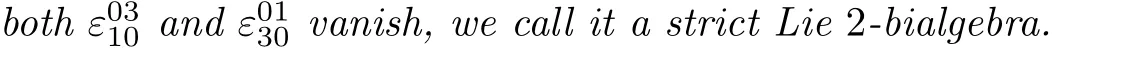
It is known that if(g,[·,·],δ)is a Lie bialgebra,then(g,[·,·])is a Lie algebra and(g,δ)is a Lie coalgebra.Similarly,we have the following lemma which can also be found in[1].

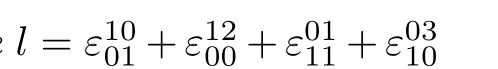
In the view of the proof of Lemma 3.2 below,this fact can be obtained easily.

3.2 Main Theorem

Before we state and prove our main theorem,we give the following lemma.

Lemma 3.2If(θ,g;ϵ)is a Lie2-bialgebra,then it is equivalent to the following equations:

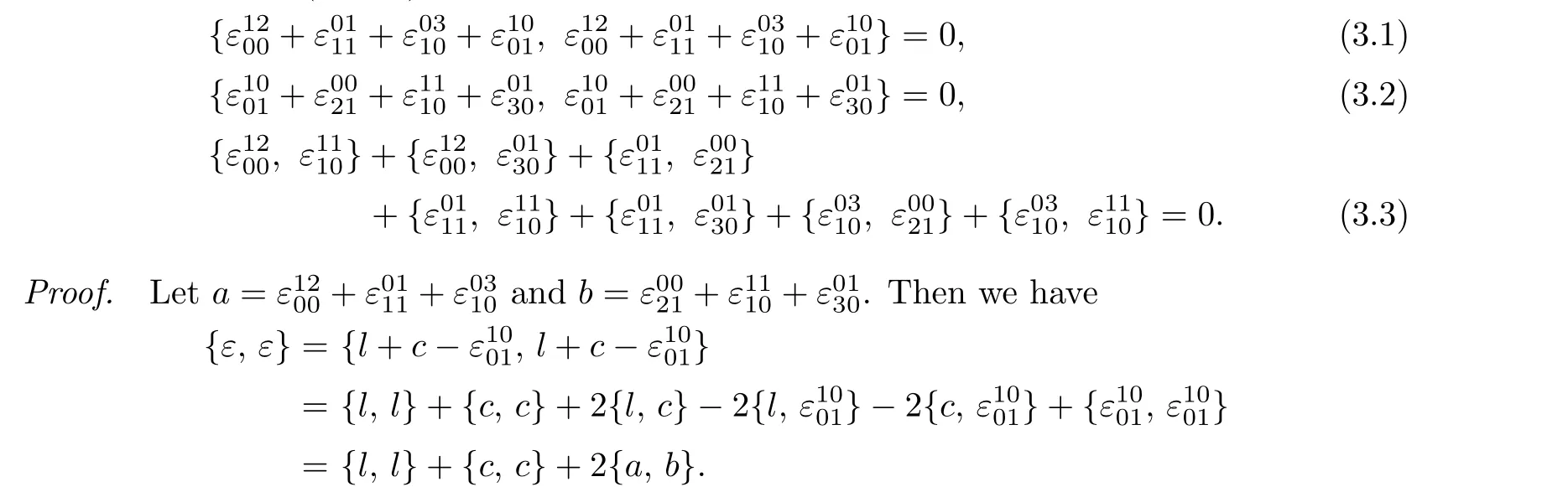
By examining each component,we have that{l,l}∈Sp(V∗[1])⊙V[2],{c,c}∈Sq(V[2])⊙V∗[1]and{a,b}∈Sk(V∗[1])⊙Sl(V[2]),wherep,q,k,l≥2.

Hence,we have{ϵ,ϵ}=0 if and only if{l,l}=0,{c,c}=0 and{a,b}=0.Expanding these three terms gives the desired result.The proof is completed.

Our main theorem is now ready to be stated.

Theorem 3.1Given a Lie2-coalgebra structure(δ,ω,η)on a Lie2-algebra(θ,g;ϕ,[·,·],·≻·,h),it forms a Lie2-bialgebra if and only if the following equations are satisfied:for all x,y,z∈g,u∈θ,

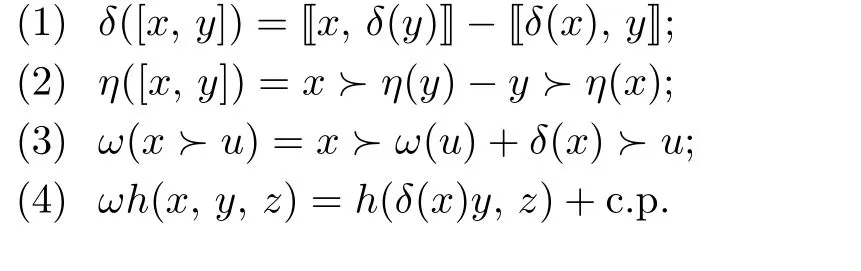
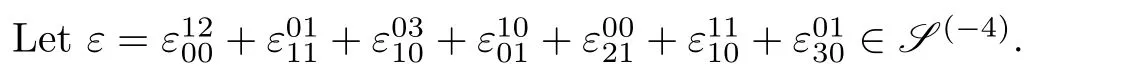
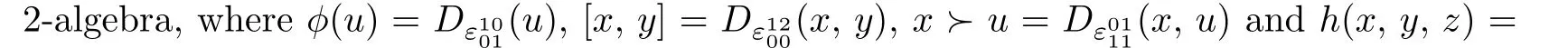
Hence,by Lemma 3.2,it suffices to prove that(3.3)is equivalent to the four conditions in this theorem.

Then the triple of linear m

aps(δ,ω,η)is introduced by:for allx∈g,u∈θ,κ,κ1,κ2,κ3∈θ∗,ξ∈g∗,

Since the left hand side of(3.3)belongs to(⊙2g∗)⊙g⊙θ+(⊙2θ)⊙g∗⊙θ∗+(⊙2g∗)⊙(⊙3θ)+(⊙3g∗)⊙(⊙2θ),we have

Hence,it follows that(3.3)is equivalent to that the triple(δ,ω,η)satisfies four compatibility conditions.This concludes the proof.

In the following,we give two examples of Lie 2-bialgebras to end up this paper.The first is a strict one.

Example 3.1Consider a 2-term complex(g→g/h,π),where g is a Lie algebra and h is one of its ideal andπis the canonical map.Equip the trivial action of g on g/h,then(g→g/h,π)is a strict Lie 2-algebra.

As in[3],any Lie 2-bialgebra structure underlying(g→g/h,π)is equivalently assigning a Lie 2-algebra structure on((g/h)∗→g∗,πT).

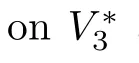
[1]Chen Z,Stienon M,Xu P.Weak Lie 2-bialgebras,J.Geom.Phys.,2013,68:59–68.

[2]Baez J C,Crans A S.Higher-dimensional algebras VI:Lie 2-algebras.Theory Appl.Categ.,2003,301:492–538.

[3]Bai C M,Sheng Y H,Zhu C C.Lie 2-bialgebras.Comm.Math.Phys.,2013,320:149–172.

[4]Chen Z,Stienon M,Xu P.Posisson 2-groups.J.Differential Geom.,2013,94:209–240.

[5]Kravchenko O.Strongly homotopy Lie bialgebras and Lie quasi-bialgebras.Lett.Math.Phys.,2007,81:19–40.

[6]Liu Z J,Sheng Y H,Zhang T.Deformations of Lie 2-algebras.J.Geom.Phys.,2014,86:66–80.

[7]Lada T,StasheffJ.Introduction to sh Lie algebras for physicists,Internat.J.Theoret.Phys.,1993,32(7):1087–1103.

[8]Lang H L,Liu Z J.Crossed modules for Lie 2-algebras.Appl.Categ.Structure,2016,24:53–78.