Reversible Properties of Monoid Crossed Products

YIN YUEZHAO LIANGAND GU QIN-QIN

(1.School of Mathematics&Physics,Anhui University of Technology,Maanshan,Anhui,243032)

(2.School of Mathematics Sciences,Nanjing Normal University,Nanjing,210046)

Communicated by Du Xian-kun

1 Introduction

Throughout,unless otherwise indicated,Rdenotes an associative ring with identity andMis a monoid.In[1],Cohn introduced the notion of a reversible ring.A ringRis said to be reversible ifab=0 impliesba=0 for alla,b∈R.Anderson and Camillo[2]used the term ofZC2for what is called reversible.It was proved in[3]that polynomial rings over reversible rings need not be reversible.A ringRis called reduced if it has no non-zero nilpotent elements(see[4]),i.e.,a2=0 impliesa=0 for alla∈R.Recall from[5]that a ringRis strongly reversible if polynomialsf(x),g(x)∈R[x]withf(x)g(x)=0 impliesg(x)f(x)=0.It is clear that all reduced rings are strongly reversible,but the inverse is not true.Rage and Chhawchharia[6]introduced the concept of an Armendariz ring.AringRis an Armendariz ring,whenever polynomialsf(x)=a0+a1x+a2x2+···+anxn,g(x)=b0+b1x+b2x2+···+bmxmare inR[x]and iff(x)g(x)=0,thenaibj=0 for alli,j.In the following,we denote byR[M]the monoid ring constructed from ringRand the monoidM,andealways stands for the identity ofM.According to[7],a ringRis called anM-Armendariz ifα=a1g1+a2g2+···+angn,β=b1h1+b2h2+···+bmgm∈R[M]satisfyαβ=0,thenaibj=0 for alli,j.A ringRis stronglyM-reversible ifαβ=0 impliesβα=0 for allα,β∈R[M](see[8]).Recall from[9]that a ringRis skew stronglyM-reversible wheneverαβ=0 impliesβα=0,whereα,β∈R∗M.

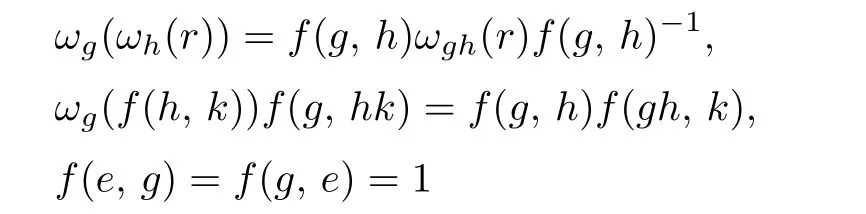
for allg,h,k∈M.

Monoid crossed products are a quite general ring construction.LetR♯Mbe a monoid crossed product with twistingfand actionω.If the twistingfis trivial,i.e.,f(x,y)=1 for allx,y∈M,thenR♯Mis the skew monoid ringR∗M.If the actionωis trivial,i.e.,ωg=iRwithiRthe identity map overR,thenR♯Mis the twisted monoid ringRτ[M].If both the twistingfand the actionωare trivial,thenR♯Mis a monoid ring,denoted byR[M].Motivated by the results of[3],[5],[8]and[9],in this paper we introduce and study the concept of stronglyCM-reversible rings,which is a generalization of strongly reversible rings,stronglyM-reversible rings and skew stronglyM-reversible rings.The main idea is to study the reversible condition defined for the monoid ring crossed productR♯M.It is shown that ifRis anM-rigid ring,thenRis stronglyCM-reversible.Moreover,ifRis a right Ore ring with classical right quotient ringQ,then we show thatRis stronglyCM-reversible if and only ifQis stronglyCM-reversible.Suppose thatR/Iis stronglyCM-reversible for someω-invariant idealIofR.IfIis anM-rigid ring,it is proved thatRis stronglyCM-reversible.Some well-known results on this subject are generalized and extended.

2 Main Results

In this section,we introduce the notion of stronglyCM-reversible rings and investigate its properties.Some characterizations of this class of rings are given.

We start with the following definition.

Definition 2.1Let R be a ring,M be a monoid with a twisting f:M×M→U(R)and an action ω:M→Aut(R).We call that the ring R is a strongly CM-reversible ring if αβ=0implies βα=0for all α,β∈R♯M.

Remark 2.1LetRbe a stronglyCM-reversible ring.Then we have the following facts:

(1)IfRis an arbitrary ring andM={e},then the trivial monoid homomorphismω:M→Aut(R)is the only monoid homomorphism and the twistingfis trivial.Clearly,Ris stronglyCM-reversible if and only ifRis stronglyM-reversible.

(2)LetM=(N,+).If the monoid homomorphismω:M→Aut(R)and the twistingfare trivial,then it is clear that a ringRis stronglyCM-reversible if and only ifRis stronglyM-reversible if and only ifRis strongly reversible.

(3)If the twistingfis trivial,then the class of stronglyCM-reversible rings is precisely the class of skew stronglyM-reversible rings.

(4)IfRis a stronglyCM-reversible ring with a trivial twistingf,then everyM-invariant subringS(i.e.,ωg(S)⊆Sfor allg∈M)is also stronglyCM-reversible.

The next proposition gives the relationship between the stronglyCM-reversible property of a ringRand that of its subrings induced by a central idempotent.

Proposition 2.1Let R be a ring,M be a monoid with a twisting f:M×M→U(R)and an action ω:M→Aut(R).If a is a central idempotent of R such that ωg(a)=a for each g∈M,then the following statements are equivalent:

(1)R is a strongly CM-reversible ring;

(2)aR and(1−a)R are strongly CM-reversible rings.Proof.(1)⇒(2).It is straightforward.

(2)⇒(1).LetaRand(1−a)Rbe stronglyCM-reversible rings.Suppose thatα=a1g1+···+angn,β=b1h1+···+bmhm∈R♯Msuch thatαβ=0.Let

It is easy to see thatα1,β1∈(aR)♯Mandα2,β2∈((1−a)R)♯M.Sinceais a central idempotent ofRsuch thatωg(a)=afor eachg∈M,we have

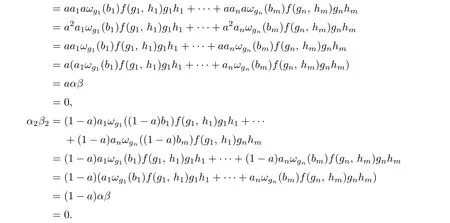
BecauseaRand(1−a)Rare stronglyCM-reversible subrings ofR,we conclude that

Therefore,we have

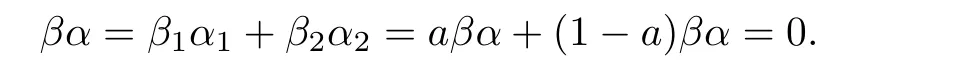
This implies thatRis stronglyCM-reversible.The proof is completed.

According to Krempa[11],an endomorphismαof a ringRis rigid ifaα(a)=0 implies thata=0 fora∈R.A ringRisα-rigid if there exists a rigid endomorphismαofR.A ringRisα-compatible if for everya,b∈R,ab=0 if and only ifaα(b)=0.By Lemma 2.2 of[12],a ringRisα-rigid if and only ifRisα-compatible and reduced.

For a ringRand a monoidMwithω:M→End(R)a monoid homomorphism,we say thatRisM-compatible(resp.,M-rigid)ifωgis compatible(resp.,rigid)for anyg∈M.

Corollary 2.1Let R be an M-compatible ring and M be a monoid with a twisting f:M×M→U(R)and an action ω:M→Aut(R).If a is a central idempotent of R,then R is strongly CM-reversible if and only if aR and(1−a)R are both strongly CM-reversible.

Proof.IfRisM-compatible,thenωg(a)=afor each idempotenta∈Randg∈Mby Lemma 2.11 of[13],and the result follows from Proposition 2.1.This completes the proof.

According to[14],a ringRis said to beCM-Armendariz ifα=a1g1+···+angn,β=b1h1+···+bmhm∈R♯Msuch thatαβ=0,thenaiωgi(bj)=0 for alli,j.

Lemma 2.1Let R be a ring and M be a u.p.-monoid with a twisting f:M×M→U(R)and an action ω:M→Aut(R).If R is M-rigid,then R♯M is reduced.

Proof.Suppose thatα=a1g1+···+angn∈R♯Msuch thatα2=0.ThenRis aCMArmendariz ring by Proposition 2.2 of[14],and thusaiωgi(aj)=0 for alli,j.Since everyM-rigid ring isM-compatible and reduced,we haveai=0 for all 1≤i≤n.It follows thatα=0.This implies thatR♯Mis reduced.

Corollary 2.2Let M be a u.p.-monoid and R be a reduced ring.Then R[M]is reduced.Proposition 2.2Let M be a u.p.-monoid with a twisting f:M×M→U(R)and an action ω:M→Aut(R).If R is an M-rigid ring,then R is strongly CM-reversible.

SinceRisM-rigid,we haveβα=0 by Lemma 2.1.HenceRis stronglyCM-reversible.

Lemma 2.2Direct products of strongly CM-reversible rings are strongly CM-reversible.Proposition 2.3Let R be a ring,M be a commutative cancellative monoid with a twisting f:M×M→U(R)and ω:M→End(R)a monoid homomorphism.Suppose that N is an ideal of M such that ωg(r)=1Rfor every g∈N and r∈R.If R is strongly CN-reversible,then R is strongly CM-reversible.

SinceRis stronglyCN-reversible,we have

This implies that

for eachi,j.Therefore,we havebjωhj(ai)=0 for alli,j,and thus

This proves thatRis stronglyCM-reversible.

Example 2.1LetRbe a ring with unity andM={e,g,g2,···,gn−1}a cyclic group of ordern.Let

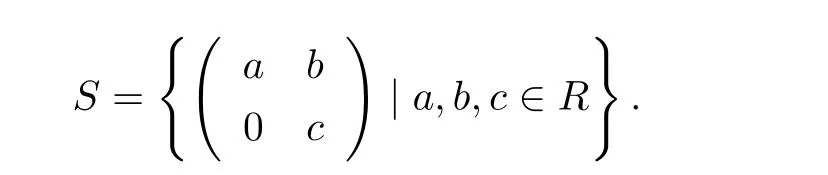
If the twistingfis trivial(i.e.,f(x,y)=1 for allx,y∈M),thenSis not stronglyCM-reversible.In fact,let

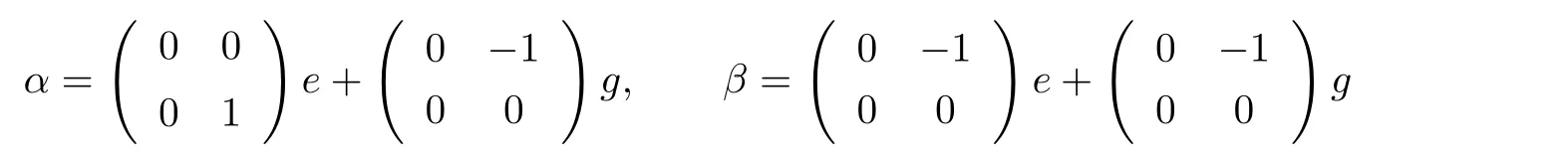
be elements inS♯M.It is easy to see thatαβ=0.But

This implies thatβα/=0.Therefore,Sis not stronglyCM-reversible.

Lemma 2.3Let M be a monoid and N be a submonoid of M.If R is a strongly CM-reversible ring,then R is strongly CN-reversible.

Lemma 2.4[7]If M and N are u.p.-monoids,then so is M×N.

LetT(G)be the set of elements of finite order in an Abelian groupG.ThenT(G)is fully invariant subgroup ofG.Gis said to be torsion-free ifT(G)={e}.

Theorem 2.1Let G be a finitely generated Abelian group.Then the following conditions on G are equivalent:

(1)G is torsion-free;

(2)There exists a ring R with|R|≥2such that R is strongly CG-reversible.

(1)⇒(2).LetGbe a finitely generated Abelian group withT(G)={e}.ThenG=Z×Z×···×Z is a finite direct product of group Z.By Lemma 2.4,Gis a u.p.-monoid.IfRis a commutativeM-rigid ring,thenRis stronglyCG-reversible by Proposition 2.2.

Proposition 2.4Let M be a cancellative monoid with a twisting f:M×M→U(R)and an action ω:M→Aut(R).Then R is strongly CM-reversible if and only if△−1R is strongly CM-reversible.

Proof.It suffices to show the necessity.Assume thatRis stronglyCM-reversible.Let

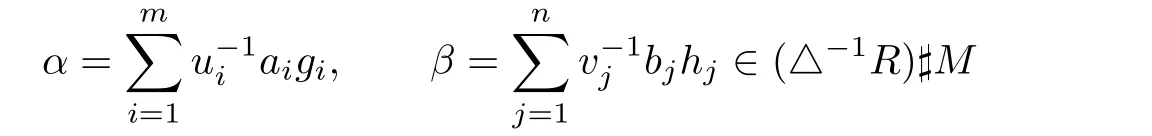
such thatαβ=0.Since△is a multiplicative monoid consisting of central regular elements ofR,we have

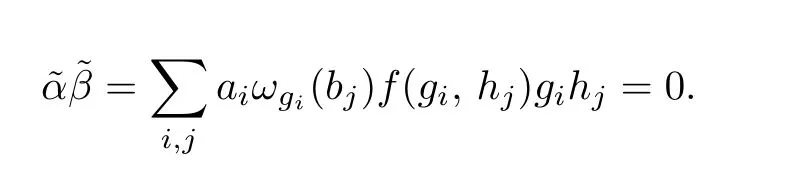
SinceRis stronglyCM-reversible,we have

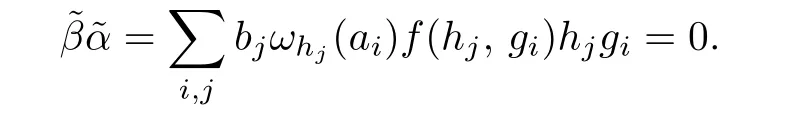
This implies that

sinceui,vjare central regular elements ofR.

For a ringSandn≥2,let

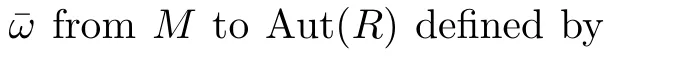
The following example shows that there exists a ringRsuch thatR/Iis stronglyCM-reversible for every non-zero stronglyCM-reversible proper idealI(as a ring without identity),butRis not stronglyCM-reversible.

Example 2.2LetSbe a division ring,and

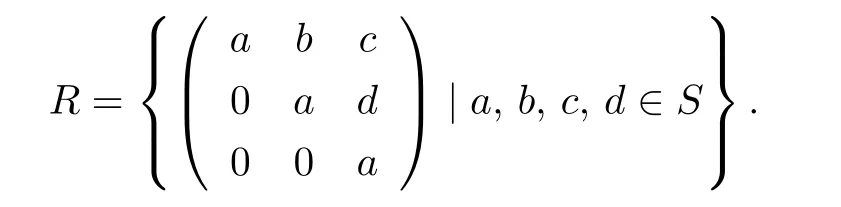
It is clear thatRis not stronglyCM-reversible since it is not a reversible ring.LetMbe a monoid with|M|≥2.Take a non-zero proper ideal

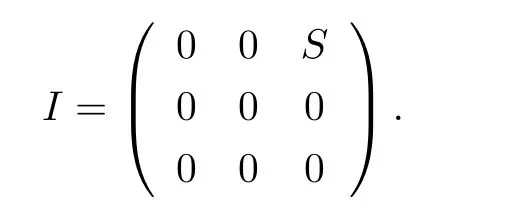
It is easy to see thatIis a stronglyCM-reversible ideal ofR.Next we show thatR/Iis a stronglyCM-reversible ring.To this end,if

are elements in(R/I)♯Msuch thatαβ=0,then we have

Therefore,we have

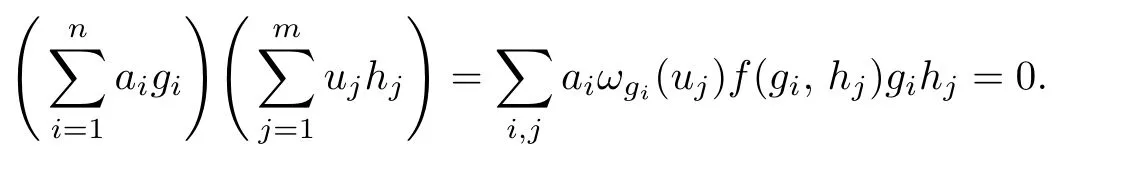
However,we have an affirmative answer as the following proposition.

Proposition 2.5Let R be a ring and M be a monoid with a twisting f:M×M→U(R)and an action ω:M→Aut(R).Suppose that R/I is strongly CM-reversible for some ωinvariant ideal I of R.Ifiis M-rigid,then R is strongly CM-reversible.

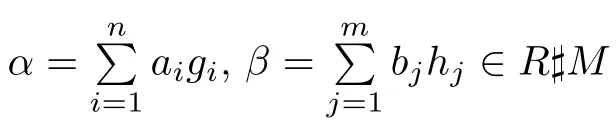
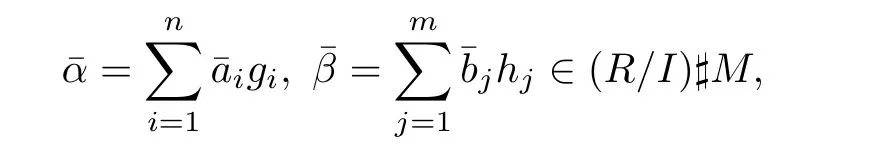
in(R/I)♯M.Therefore,we have

sinceR/Iis stronglyCM-reversible,and thusβα∈I♯M.SinceIis anM-rigid ring,I♯Mis reduced by Lemma 2.5.It follows that

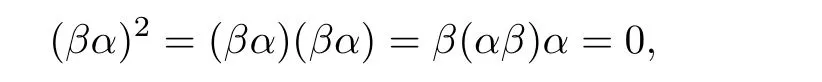
which implies thatβα=0.This shows thatRis a stronglyCM-reversible ring.

It was shown in Theorem 2.6 of[3]that a ringRis reversible if and only if its classical right quotient ring is reversible.Moreover,the authors of[15]also proved that a ringRis strongly rightα-reversible if and only if its classical right quotient ring is strongly rightα-reversible.More generally,we have the following theorem.

Theorem 2.2Let M be a monoid with a twisting f:M×M→U(R)and an action ω:M→Aut(R).If R is a right Ore ring with a classical right quotient ring Q,then R is strongly CM-reversible if and only if Q is strongly CM-reversible.

sinceωhjis an automorphism ofRfor eachhj.Therefore,we haveα1β2=0,and henceα1β1=0 inR♯M.

It follows thatα2β1=0 inR∗M,and thusβ1α2=0 sinceRis a stronglyCM-reversible ring.Therefore,we have

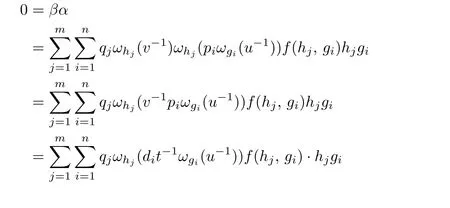
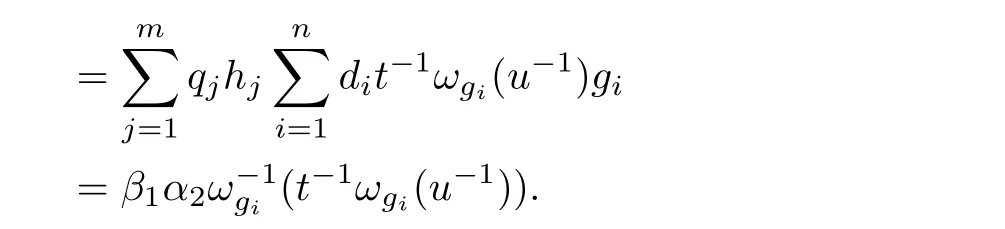
By the definition of a stronglyCM-reversible ring,Qis a stronglyCM-reversible ring and we are done.

Proposition 2.6Let M be a monoid with a twisting f:M×M→U(R)and an action ω:M→Aut(R).If R is an M-rigid CM-Armendariz ring,then R is strongly CM-reversible.

Proof.Letα=a1g1+a2g2+···+angn,β=b1h1+b2h2+···+bmhm∈R♯Msuch thatαβ=0.SinceRisCM-Armendariz,we getaiωgi(bj)=0 for alli,j.This implies thataibj=0 for alli,jsinceRisM-compatible.BecauseRis a reversible ring,bjai=0 for alli,j.Thenbjωhj(ai)=0 for alli,j,and hence

This implies thatRis stronglyCM-reversible.

[1]Cohn P M.Reversible rings.Bull.London Math.Soc.,1999,31:641–648.

[2]Anderson D D,Camillo V.Semigroups and rings whose zero products commute.Comm.Algebra,1999,27(6):2847–2852.

[3]Kim N K,Lee Y.Extension of reversible rings.J.Pure Appl.Algebra,2003,185(1):207–223.

[4]Kim N K,Lee Y.Armendariz rings and reduced rings.J.Algebra,2000,223(2):477–488.

[5]Yang G,Liu Z K.On strongly reversible rings.Taiwanese J.Math.,2008,12(1):129–136.

[6]Rage M B,Chhawchharia S.Armendariz rings.Proc.Japan.Acad.Ser.A Math.Sci.,1997,73:14–17.

[7]Liu Z K.Armendariz rings relative to a monoid.Comm.Algebra,2005,33(3):649–661.

[8]Singh A B,Juyal P,Khan M R.Strongly reversible rings relative to a monoid.J.Pure Appl.Algebra,2010,63(1):1–7.

[9]Peng Z M,Gu Q Q,Zhao L.On skew strongly reversible rings relative to a monoid.J.Math.Res.Appl.,2016,36(1):43–50.

[10]Kelarev A V.Ring Constructions and Applications.Singapore:World Scientific Publishing Co.Pte.Ltd.,2002.

[11]Krempa J.Some examples of reduced rings.Algebra Colloq.,1996,3(4):289–300.

[12]Hashemi E,Moussavi A.Polynomial extensions of quasi-Baer rings.Acta Math.Hungar.,2005,107(3):207–224.

[13]Habibi M,Manaviyat R.A generalization of nil-Armendariz rings.J.Algebra Appl.,2013,12(6):1–30.

[14]Zhao L,Zhou Y Q.Generalized Armendariz properties of crossed product type.Glasgow Math.J.,2016,58:313–323.

[15]Zhao L,Zhu X S.Extensions of stronglyα-reversible rings.Bull.Iranian.Math.Soc.,2012,38(1):275-292.

[16]Mcconnell J C,Robson J C.Noncommutative Noetherian Rings.New York:Wiley,1987.