微载荷连续球压痕法评价金属材料的屈服强度和应变硬化指数
,
(南京工业大学机械与动力工程学院, 南京 211816)
0 引 言
石油化工、核电等领域中需要用到大量的承压设备,这些设备的工作环境大多为高温、高压甚至存在腐蚀介质,这对承压设备提出了极高的要求,为保证设备的安全运行,需要对设备用材料的力学性能进行在役检测。然而,传统的单轴拉伸试验方法和以小冲杆试验为代表的微试样试验方法均需要从在役设备上取样,这将对设备造成一定的伤害,因此其实际应用范围受到一定的限制[1]。球压痕法作为一种新的测试方法,在测试过程中几乎不会对设备造成任何伤害,非常适合用于检测在役设备材料的力学性能,因此球压痕法近年来得到了越来越多的关注[2]。
FIELD等[3]利用球压痕法,提出了测金属材料的硬度、弹性模量、应力-应变曲线和应变硬化指数[4]等的方法。KUCHARSKI等[5]也利用球压痕法,提出了一个新的系统性测试金属材料应力-应变曲线的方法。这两种方法虽然都用于测试金属材料,但仍有不同之处。在FIELD等提出的方法中,压头的下压深度以纳米为单位,最大下压深度约为1.2 μm,在此深度下需考虑尺度效应的影响[6],但FIELD等并未对尺度效应进行讨论。在KUCHARSKI等提出的方法中,压头的下压深度以微米为单位,因此可忽略尺度效应。这两种方法均是基于硬度测试原理发展而来的,需要获取加载及卸载时的载荷以及压头与材料的接触面积,因此需考虑在压头下压材料过程中,材料被压区域所产生的塑性鼓凸(pile-up)或凹进(sink-in)现象,但FIELD等忽略了此现象的影响,而KUCHARSKI等虽然考虑了塑性鼓凸或凹进的影响,但不够准确,仍需进一步的研究。HERNOT等[7]采用数值模拟方法确定了大部分金属材料由球形压头产生的塑性区周围压入深度和接触半径之间的关系,但仍不能很好地解决此问题,并且计算过程较为繁琐。
CAO等[8]将DAO等[9]在锥形压头压痕法中提出的表观应变概念引入到了球形压头压痕法中,并提出了一个新的分析框架,同时通过对24种已知性能参数材料的压痕过程模拟和根据分析获得的载荷、压痕深度数据,得出给定压入深度下不随应变硬化指数改变的无量纲函数及对应的表观应变,最后将试验获得两次压入深度的载荷带入无量纲函数来计算材料的屈服强度和应变硬化指数。CAO等的方法只需利用压痕深度和对应的载荷来计算材料的性能参数,从而避免了接触面积不好确定及计算不准确的问题。但CAO等的方法仅在应用于屈服应变为0.001 43~0.015 39范围内的金属材料时才可获得较准确的结果。虽然崔航等[10]在CAO等的研究基础上,采用同样的方法补充了屈服应变为 0.007 69~0.040 00范围内金属材料性能的计算公式,但其应用范围仍有一定的局限性。
为了使CAO等的计算方法更适用于在役设备材料的检测以及适用于更多的金属材料,作者对CAO等的方法进行了改进,采用球形压头连续加载方法代替CAO等使用的球形压头单次加载法,采用量纲分析法和有限元模拟得到无量纲函数及其表观应变规律,并计算材料的屈服强度和应力-应变曲线,同时对文献[10]以外的金属材料进行了分析,补充了屈服应变在0.000 95~0.002 00范围内金属材料性能的计算公式,然后对该计算方法进行了试验验证。

图1 具有应变硬化特征的应力-应变曲线Fig.1 Stress-strain curve with strain hardening characteristics
1 力学模型及数学模型
1.1 力学模型
对于大多数的金属材料而言,在均匀塑性变形阶段的应变硬化行为均可用简单地用Ludwik或Hollomon方程来描述。图1为具有应变硬化特征材料的应力-应变曲线,可用下式进行描述。
(1)
ε=εy+εp
(2)
当σ>σy时,应力σ也可表示成
(3)
式中:σy为初始屈服强度;ε为总应变;εy为初始屈服应变;εp为塑性应变;E为弹性模量;K为强度系数;n为应变硬化指数。
1.2 表观应变的定义
DAO等[9]和CHOLLACOOP[11]在研究锥形压头时提出了表观应变概念,即在给定压入深度下,存在一个应变使得无量纲函数П1与E*/σr(E*为有效弹性模量,σr为表观应力)相关,与应变硬化指数n无关,这个应变被定义为表观应变εr。令εp=εr,代入式(3)中,即得到表观应变对应的表观应力σr。
CAO等对24种弹塑性金属材料球形压头压痕测试进行了有限元模拟,找到了与压入深度相关,但与应变硬化指数n无关的表观应变εr,并给出了无量纲函数П1。崔航等[10]在CAO和LU研究结果的基础上对56种弹塑性金属材料进行了分析,给出了使用范围更广的表观应变εr和无量纲函数П1。
1.3 量纲分析及数学模型
量纲分析法是球形压头压痕试验中经常使用的一种分析方法。CHENG等[12]在分析有限元模拟方法获得数据的基础上,建立了许多无量纲函数。在CAO等和崔航等[10]的研究中也均采用量纲分析与有限元分析相结合的方法来获取材料的力学性能。因此,作者同样也采用基于无量纲函数和有限元分析相结合的方法进行研究。
在加载过程中,压入载荷P可以通过几个相关参数的函数式来表达。
P=f(E,ν,Ei,νi,σy,n,h,R)
(4)
式中:E为被测金属材料的杨氏模量;ν为材料泊松比;σy为屈服强度;n为应变硬化指数;Ei为压头材料的弹性模量;νi为压头的泊松比;R为压头半径;h为压痕下压深度。
1.2.1 不同因素对甜菜苷类色素提取率的影响 色素提取工艺流程:新鲜原料→去除外层果皮→将果皮打碎→加入溶剂浸泡并搅拌→离心分纯→过滤→真空浓缩→色素溶液。
引入有效弹性模量E*(reduced Young′s modulus)后,可得到
P=f(E*,σy,n,h,R)
(5)
式(4)可以写成
(6)
引入表观应变εr对应的应力σr,式(5)可以写成
P=f(E*,σr,n,h,R)
(7)
П定理作为量纲分析的核心理论,可以提供在不知道等式具体形式的情况下由所给变量计算无量纲参数的方法。根据П定理可得
(8)
由于压痕深度hg和压头半径R已给定,可得到
(9)
2 有限元模型的建立
采用ABAQUS有限元仿真软件进行压痕试验模拟,考虑到模型结构和载荷的对称性,将试验过程简化为二维轴对称模型。根据圣维南原理,远离压痕区域处的应力和应变趋近于零,且实际试样尺寸远大于压痕区域尺寸,因此为减少模型的单元数目,节约计算成本,模拟只需建立局部材料模型,即模型尺寸远小于实际试样尺寸。模型中球形压头的半径为0.5 mm,试样尺寸为5 mm×5 mm。
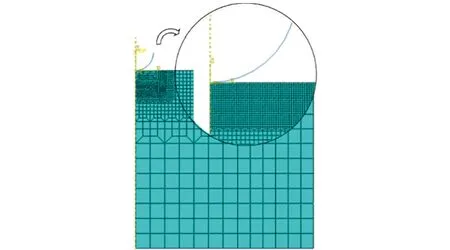
图2 有限元模型网格划分Fig.2 Finte element mesh generation
在压痕试验模拟中,变形主要集中在压头与试样接触区域,因此采用相关文献[13]中的过渡网格来划分模型单元,如图2所示。由于网格细分程度兼顾计算精度与效率,因此在靠近压头的区域网格较密,随着与压头距离的增大,网格逐渐稀疏,从模型接触区到边界,单元尺寸逐渐增大。整个模型网格包括2 280个单元,单元类型为CAX4R。边界条件采用底面固定,对压头参考点施加载荷。通过控制位移方式实现加载,最大位移为0.05 mm,加载过程为准静态过程。
压头材料为类金刚石材料,弹性模量远大于被测材料的弹性模量。在压头模型中,球形压头设置为刚体。材料模型遵循Von Mises屈服准则、各向同性强化准则以及大变形准则。试样所选材料为屈服应变为0.007 69~0.040 00范围内的钢,弹性模量为190~210 GPa,泊松比设置为0.3,模拟中各弹塑性能参数的设置如表1所示。

表1 有限元模拟中金属材料的弹塑性能参数Tab.1 Parameters of elastic-plastic properties of metalmaterials in finite element simulation
3 模拟结果与分析
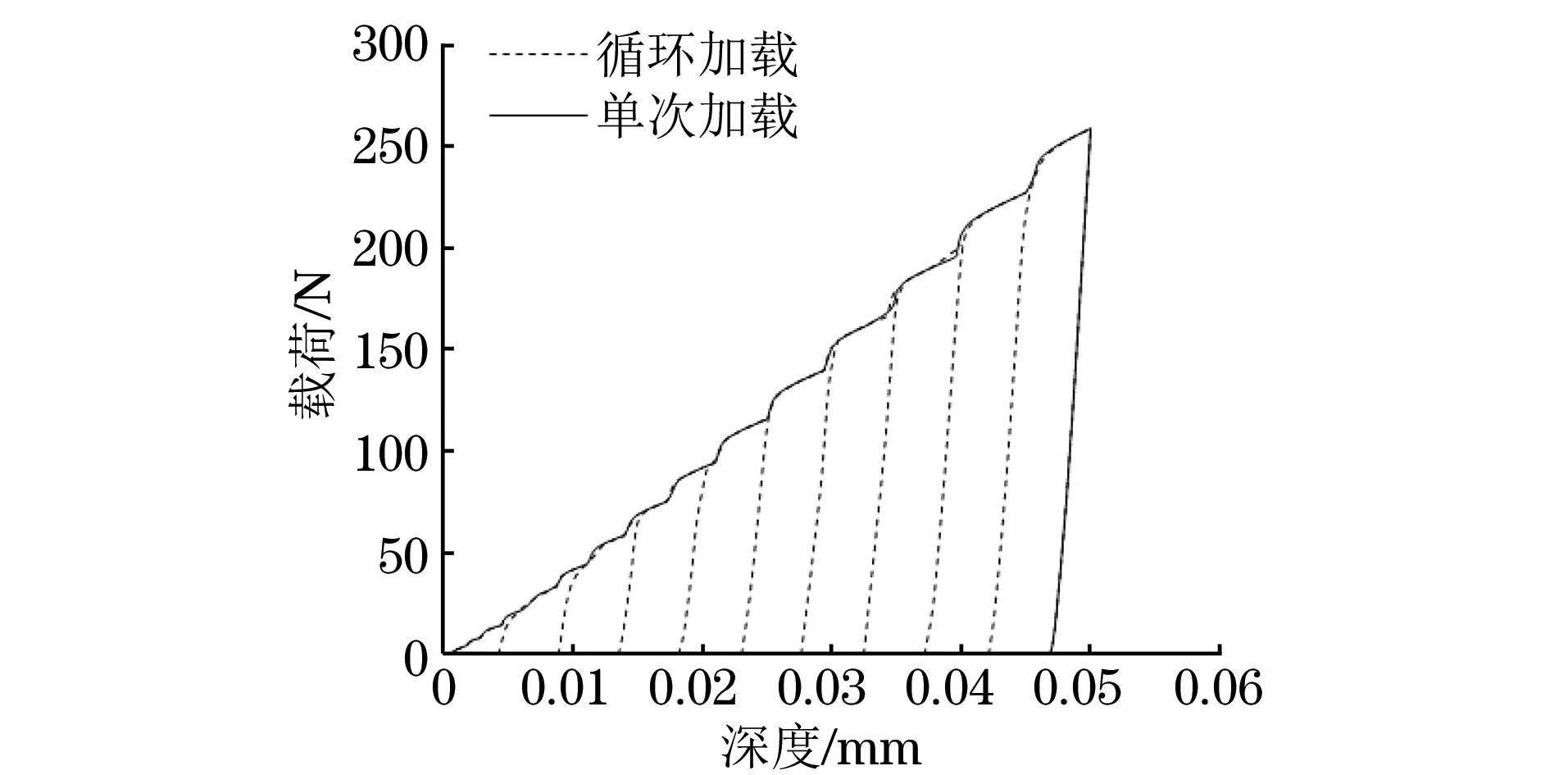
图3 单次加载-深度曲线与多次循环加载-深度曲线的对比Fig.3 Comparison of single load-displacement curve and cyclic load-displacement curve
3.1 连续循环加载载荷-深度曲线与单次加载载荷-深度曲线对比
连续循环加载是指对一个点进行往复循环加卸载,每次下压的深度不同。单次加载是指对材料只进行一次加卸载。CAO等采用的加载方法为对材料上多点进行单次加载,每次下压深度不同。作者采用的方法是对材料的一点进行往复循环加卸载,所得到的载荷-深度曲线如图3所示。由图可以发现,连续循环加载所得到的载荷-深度曲线与单次加载获得的载荷-深度曲线基本吻合。因此,在采用CAO等的计算方法时,可以采用连续循环加载方法代替多点单次加载方法来得到不同深度下的载荷,简化了采用球形压痕法获取载荷-深度曲线的步骤。
3.2 摩擦因数对载荷-深度曲线的影响
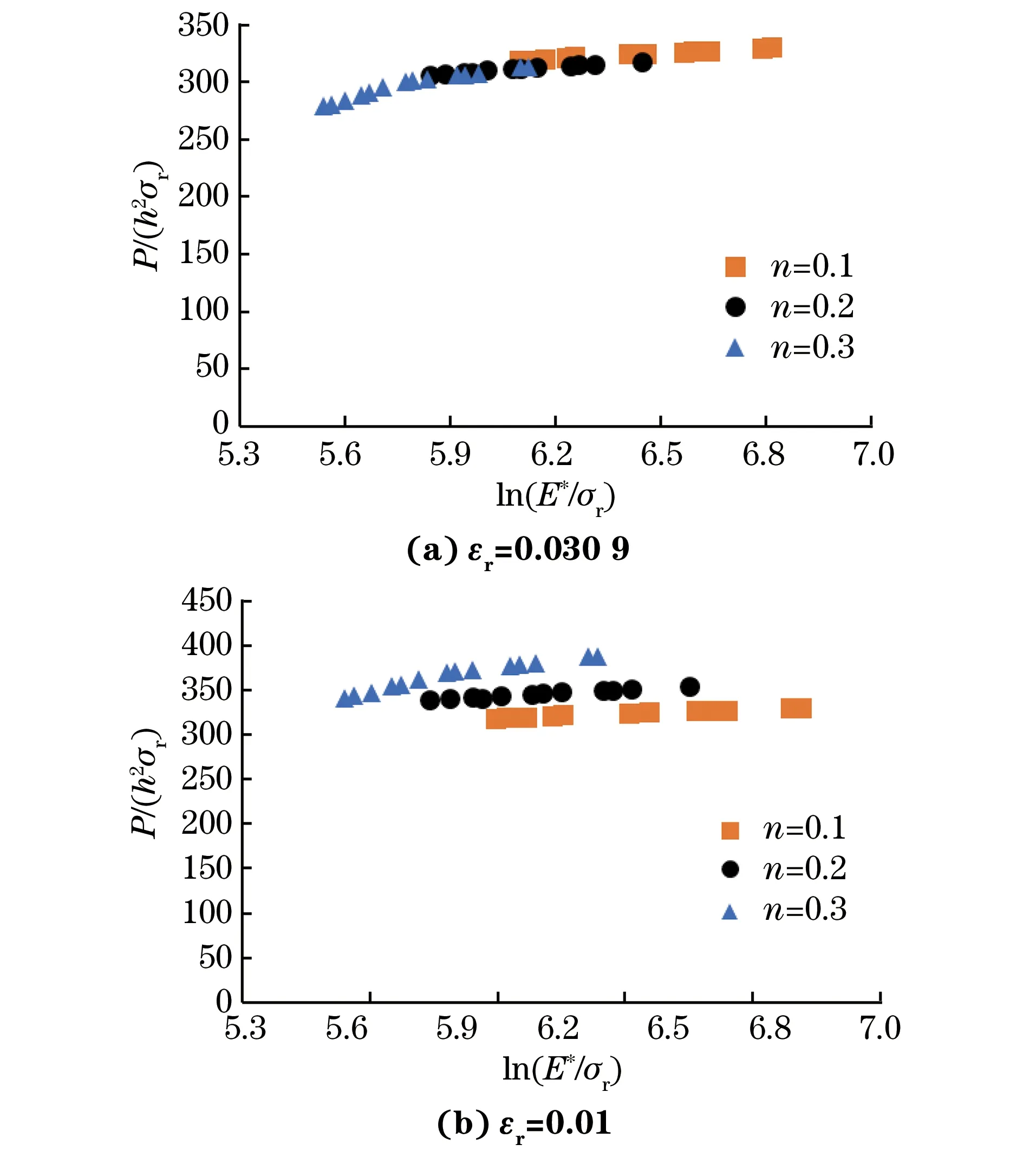
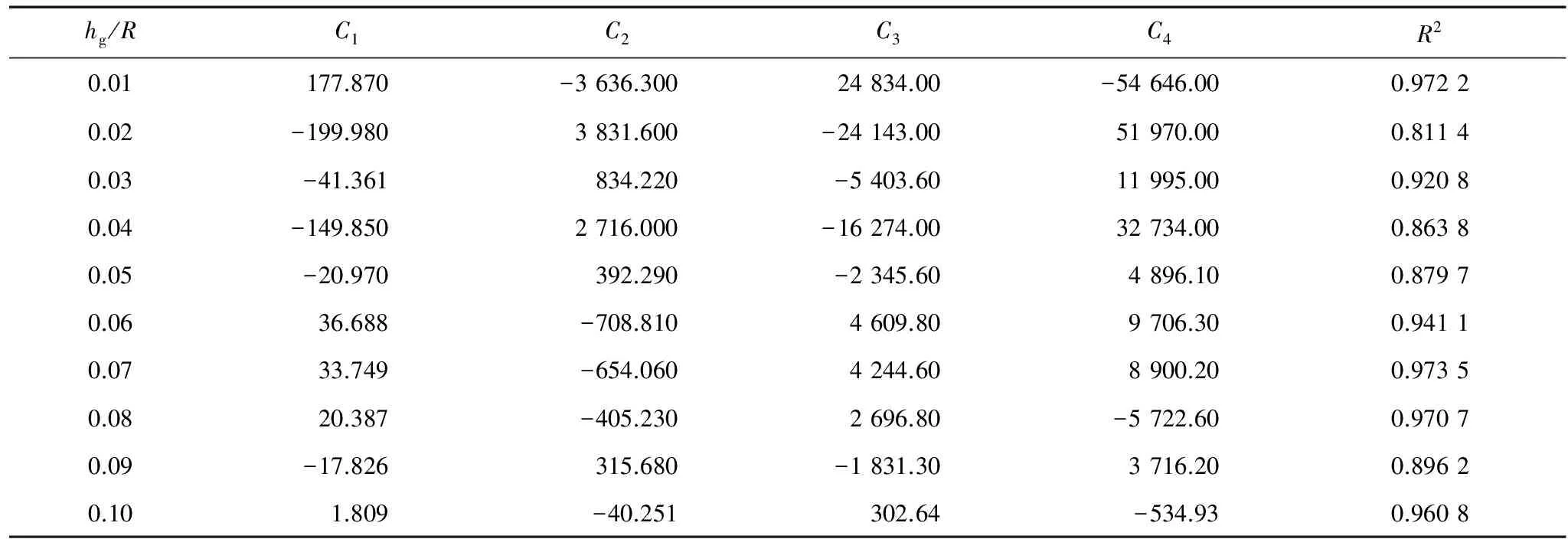
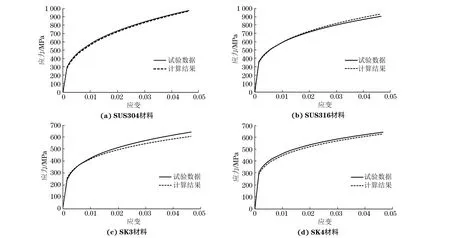
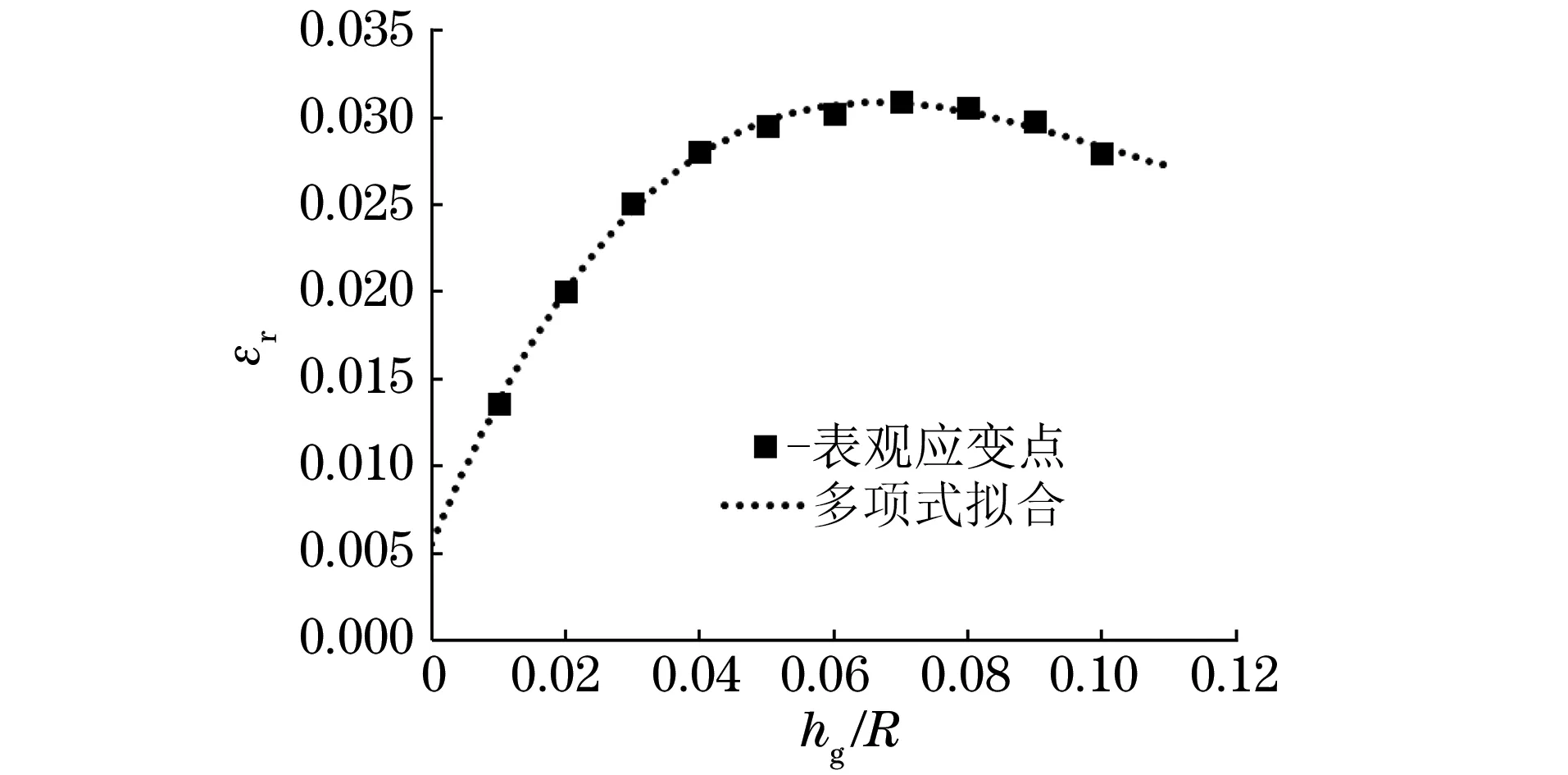
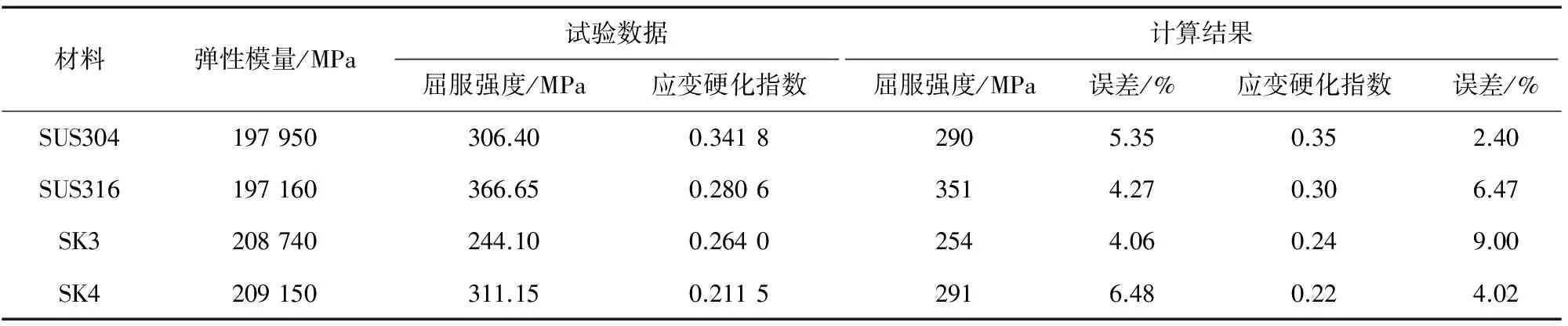
压头与试样接触时会存在摩擦,但不能确定摩擦因数μ的大小。文献[14]中讨论了摩擦因数对微压痕试验的影响,认为摩擦因数对载荷-深度曲线的影响可以简化。文献[10]提出了当压入深度满足0.01 图4 不同摩擦因数下单次加载-位移曲线Fig.4 Single load-displacement curve for different friction factors 图5 不同摩擦因数下循环加载-位移曲线Fig.5 Cyclic load-displacement curve for different friction factors 对45种已知参数的金属材料进行压痕试验模拟,对得到的载荷-深度曲线进行处理,得到不同深度下对应的表征应变,然后用三次多项式可拟合出无量纲函数П1,其公式为 (10) 式中:C1,C2,C3,C4为系数,在不同hg/R下其取值也不同。 以hg/R=0.07为例来阐述表观应变的确定方法。图6为压痕深度hg/R=0.07时,不同应变对无量纲函数П1的影响。由图可以看出,当εr=0.030 9时,无量纲函数П1与应变硬化指数n无关。因此,0.030 9为直径为1 mm的压头在下压深度0.035 mm、hg/R=0.07时所对应的表观应变。对图6(a)中各点进行拟合,所得函数即为hg/R=0.07时无量纲函数П1的表达式。 图6 hg/R=0.07时不同应变硬化指数和表观应变下的无量纲函数Fig.6 Dimensionless function for different strain hardening exponent and representative strain at hg/R=0.07 对材料进行10次压入模拟,每次间隔距离均为0.005 mm,可获得10次不同深度所对应的表观应变。采用三次多项式对不同深度时的表观应变进行拟合,得到式(11),不同hg/R对应的表观应变如图7所示。根据不同深度下的表观应变,对各点进行拟合即可求出不同深度下无量纲函数П1表达式的系数,如表2所示。 (11) 表2 不同hg/R下无量纲函数的系数Tab.2 Coefficients of dimensionless function for various hg/R 图8 不同金属材料应力-应变曲线的计算结果与试验数据的对比Fig.8 Comparison of stress-strain curves of different metal materials between calculation results and test data 图7 不同hg/R对应的表征应变Fig.7 Representative strain corresponding to various hg/R 通过对文献[15]中已知弹塑性参数的金属材料进行模拟得到载荷-深度曲线,然后采用无量纲函数式(9)~式(11)进行计算,得到的屈服强度及应变硬化指数结果列于表3中。由表可以看出:屈服强度计算结果与试验数据的最大误差为6.48%,最小误差为4.06%,平均误差为5.04%;应变硬化指数计算结果与试验数据的最大误差为9.00%,最小误差为2.40%,平均误差为5.47%。 将金属材料屈服强度和应变硬化指数的试验数据和计算结果分别带入式(1)~式(3)中,得到的应力-应变曲线如图8所示。由图可知,由该方法得到不同金属材料的应力-应变曲线与由试验数据得到的基本吻合。由此可见,采用该方法可以获得较精确的结果。 表3 屈服强度和应变硬化指数的计算结果与试验数据的比较Tab.3 Comparison of yield strength and strain hardening exponent between calculation results and test data (1) 对CAO等的方法进行了改进,采用连续循环加卸载方法代替多点单次加载法来获得不同深度下的载荷,简化了采用球形压痕法来获得载荷-深度曲线的步骤;当压痕深度满足0.01 (2) 以球形压头压痕理论为基础,采用量纲分析和有限元分析相结合的方法,拟合出了压头压入金属材料过程中的无量纲函数及对应的表观应变函数;通过拟合公式计算得到的弹塑性参数与试验结果相比,其误差均为5%左右,且两者的应力-应变曲线基本吻合。 [1] 关凯书,邹镔,伍声宝. 连续球压痕法评价钢的塑性[J]. 机械工程材料, 2016,40(9):18-21. [2] 伍声宝,徐彤,喻灿,等.采用球压痕法测16MnR钢的拉伸性能[J].机械工程材料, 2015,39(1):82-85. [3] FIELD J S, SWAIN M V. Determining the mechanical properties of small volumes of material from submicrometer spherical indentations[J]. Journal of Materials Research, 1995, 10(1):101-112. [4] THAI-HOAN P, JUNG J K, SEUNG-EOCK K. Estimating constitutive equation of structural steel using indentation[J]. International Jounal of Mechanical Sciences, 2015, 90:151-161. [5] KUCHARSKI S, MROZ Z. Identification of plastic hardening parameters of metals from spherical indentation tests[J]. Journal of Engineering Materials &Technology,2001,318(1/2):65-76. [6] 马增胜,周益春,龙士国. 纳米压痕法表征金属薄膜材料的力学性能[D].湘潭:湘潭大学,2011:58-75. [7] HERBERT E G, PHARR G M, OLIVER W C,etal. On the measurement of stress-strain curves by spherical indentation[J].Mrs Online Proceedings Library,2001,s398/399:331-335. [8] CAO Y P, LU J. A new method to extract the plastic properties of metal materials from an instrumented spherical indentation loading curve[J]. Acta Materialia, 2004,52: 4023-4032. [9] DAO M, CHOLLACOOP N, VLIET K J V,etal. Computational modeling of the forward and reverse problems in instrumented sharp indentation[J]. Acta Materialia, 2001,49(19):3899-3918. [10] 崔航,陈怀宁,陈静,等. 球形压痕法评价材料屈服强度和应变硬化指数的有限元分析[J]. 金属学报, 2009,45(2):189-194. [11] CLLOLLAEOOP N W. Computational and experimental study of instrumented indentation[M]. [S.l.]: Massachusetts Institute of Technology, 2004. [12] CHENG Y T, CHENG C M. Can stress-strain relationships be obtained from indentation curves using conical and pyramidal indenters[J]. Journal of Materials Research, 1999, 14(9):3493-3496. [13] HYUNGYIL L, JIN H L, PHARR G M. A numerical approach to spherical indentation techniques for material property evaluation[J]. Journal of the Mechanics and Physics of Solids, 2005,53(9):2037-2069. [14] 张帆, 黄克智, 黄永刚, 等. 摩擦因素对微压痕实验的影响[J]. 工程力学, 2006, 23(1):1-5. [15] KIM S H, LEE B W, CHOI Y,etal. Quantitative determination of contact depth during spherical indentation of metallic materials — A FEM study[J]. Materials Science and Engineering, 2006,415(1/2): 59-65.

3.3 表观函数与无量纲函数的确定
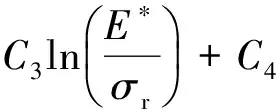
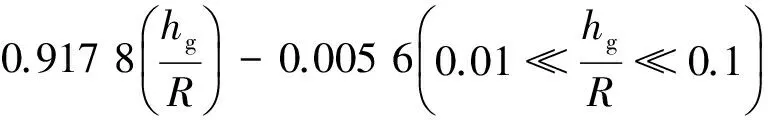
3.4 试验验证
4 结 论

