模拟移动床色谱模型的显式差分法求解
李守江,魏伯峰,丛景香,王绍艳
(辽宁科技大学 化学工程学院,辽宁 鞍山 114051)
模拟移动床(Simulated moving bed,SMB)色谱是由色谱柱串联起来的分离系统,它结合了模拟移动床技术和色谱分离技术的优点,具有分离能力强、分离效率高、易连续化生产的特点,是食品、生物和化工领域的重要分离工具[1-5]。模拟移动床是连续运行的分离装置,实际分离过程中不合理操作参数的影响都会在连续运行中放大并使分离效果变差,为了达到更好的分离效果,SMB系统的参数优化以及过程的调节一般都需要模型指导。由于SMB色谱分离模型本身的复杂性,很难解析求解,常通过相应的数学算法对其数值求解。吴献东等[6]、Zúniga等[7]通过求解真实移动床(TMB)获得模拟移动床(SMB)的数值解,危凤等[8]采用线上求解法,将色谱分离模型沿空间方向离散转换成为常微分方程组进行求解。Chen等[9]、Jiao等[10]采用有限元法求解色谱模型。姚传义等[11]采用时空守恒元解元方法对色谱分离模型离散求解。Zhang等[12]采用有限体积法求解色谱模型。叶忠建等[13]采用隐式有限差分法对线性SMB色谱模型进行了求解,并进行了仿真计算。另外,一些专业仿真模拟软件如 gPROMS[14]、Aspen Chromatography[15]等也可用于对模型求解。
本文旨在采用显式有限差分法对线性和非线性SMB色谱模型求解,并建立相关的迭代求解差分方程。在VB软件上编程计算,可获得SMB色谱模型的洗脱曲线。以SMB拆分奥美拉唑对映体的实验为例对SMB模型求解结果进行验证。另外,介绍了通过优化柱子在各区带分布提高产品分离纯度的方法。
1 模拟移动床色谱分离原理及模型
1.1 SMB结构与分离原理
SMB是多个色谱柱的串联系统,具有多进、多出的特点,通过周期性的开、关相应的进出口阀门来改变进、出口的位置,从而实现固定相与流动相的相对运行,达到分离的目的。如图1所示。由于进口与出口两侧柱中流速不同,若将流速相同的区域看成一个带。则SMB体系可划分如下:
I带:洗脱带,将慢组分解吸。
II带:精馏带,在未进样的条件下,用流动相冲洗,使快、慢组分进一步分离。
III带:吸附带,将从进样口中进来的原料吸附,使慢组分不致流出。
IV带:二精带,吸附快组分,回收流动相。
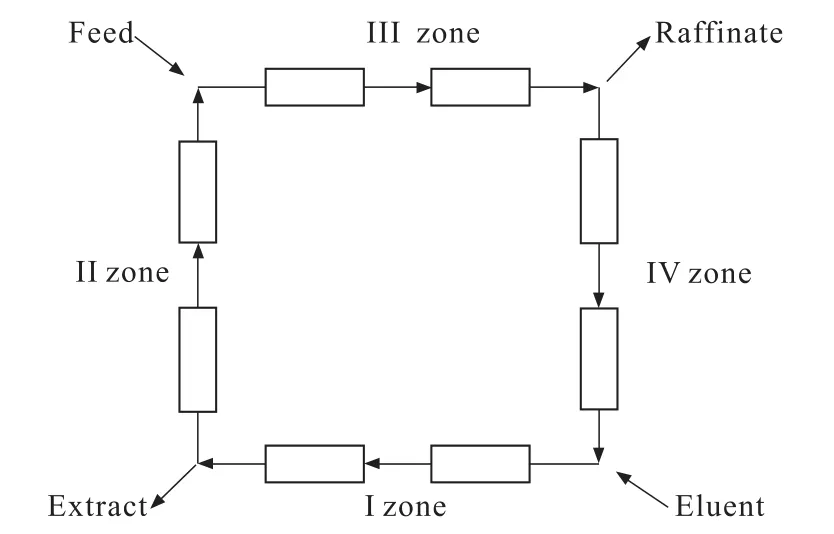
图1 SMB示意图Fig.1 SMB diagram
若SMB中固定相的运动速度为us,流动相流动速度为v,则组分i随流动相运动的通量密度为Civ,其随固定相运动的通量密度为Fusqi,如使不同组分能够分离,则快组分FusqB<CBv,慢组分Fuq>Cv,即。 v,u均与SMBsAAs进、出口阀门周期性切换的时间长短有关,其中v=u-us,u
1.2 SMB分离模型
SMB分离模型包含两部分,一部分是单柱模型,它是待分离组分在单个色谱柱内的分离情况;另一部分是节点模型,它反映了SMB各个区带之间的连接关系。
单柱色谱模型中,平衡扩散模型应用非常广泛,其模型如下
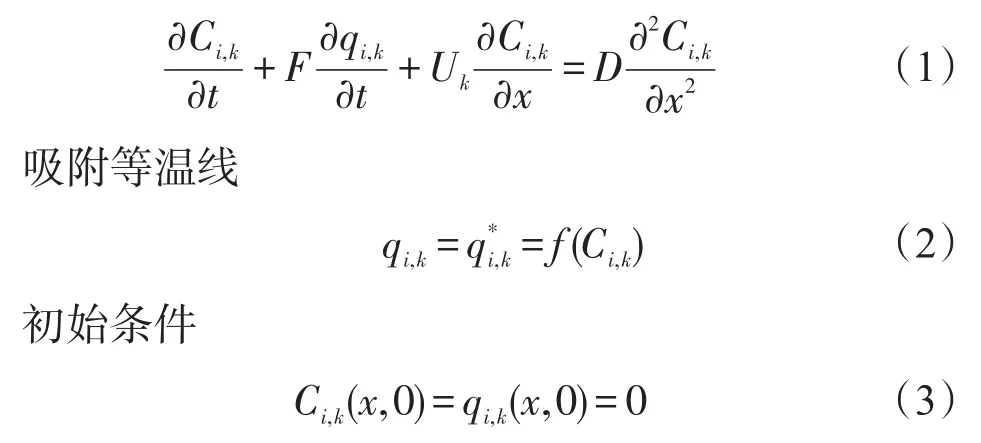
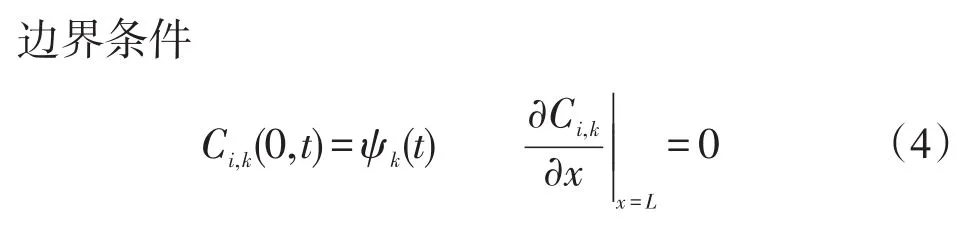
其中:i为目标组分;k为色谱柱号;U为线速度;F为相比;D为扩散系数;Ci为组分i在流动相中的浓度;q*i为平衡时组分i在固定相中的浓度;ψ(t)为进样曲线;L为色谱柱长度。
节点模型为:

2 SMB色谱模型求解
对SMB色谱模型求解可分为直接求解法[13]和间接求解法[16-17]。直接求解法一般采用高精度的差分格式直接对平衡扩散速率模型进行数值求解,间接求解法往往通过求解理想色谱模型所带来的耗散项(误差项)模拟扩散项,实现对平衡扩散速率模型的求解过程。在非线性体系下,模型易出现间断解,而高阶精度差分格式在间断点处往往存在着伪震荡[18]。一阶精度的差分格式虽然结构简单但具有很好的抑制伪震荡的效果,并且通过间接求解使其误差项与平衡扩散模型中扩散项相等的方式可以较大幅度提高计算结果的精确性。因此,本文采用间接求解法对SMB色谱模型求解。

其中:τ、h为时间和空间步长;m表示空间离散点,m=1,2,…,L/h;n为时间离散点,n=1,2,…。
将式(11)和式(12)代入式(10)中化简可得
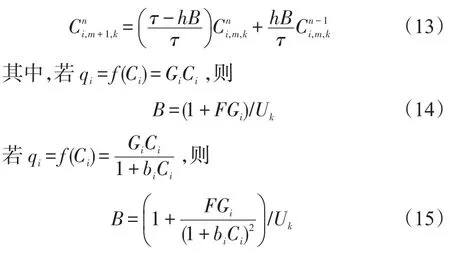
结合初始、边界条件和节点模型,对式(13)进行迭代计算可得SMB色谱模型的洗脱曲线。
3 SMB实例验证
为了验证该方法对SMB求解的可靠性,以奥美拉唑对映体的SMB分离进行验证。相关参数来自文献[8],实验操作参数见表1,对SMB计算时进行了100次切换,模拟结果见表2,其实验2的累积模拟洗脱曲线如图2所示。模拟计算时纯度定义如下:
强组分A在E口纯度
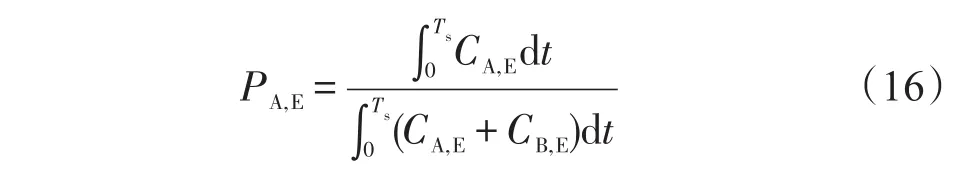
弱组分B在R口纯度

其中,Ts为切换时间;Ci为组分i在洗脱曲线上的浓度。
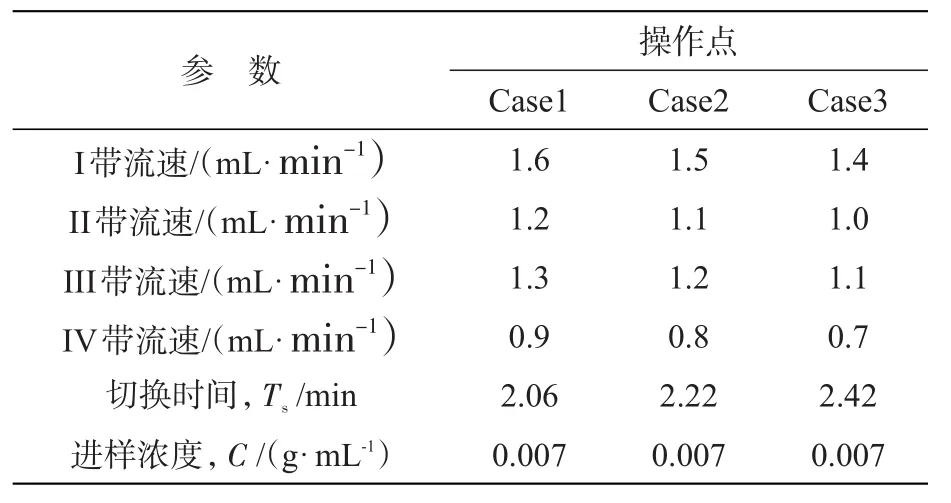
表1SMB操作参数Tab.1 SMB operating parameters

表2SMB实验与模拟结果比较,%Tab.2 Comparison of experimental and simulated results,%
由表2可知,模拟计算结果与实验结果基本吻合,验证了本方法的可靠性。
4 提高分离纯度的操作方法
从表2中的分离实验结果可以看出,目标组分在E口处的分离纯度较差,若提高其分离纯度,常用方法有:调节操作参数;优化色谱柱在各区带的分布方式;采用新型的SMB分离工艺。这里对后两种方法进行简要讨论。
4.1 增加II带、III带色谱柱个数
在SMB分离过程中,II带和III带是SMB分离的主体,通过增加II带和III带柱子的个数可以提高SMB的分离效果。上述奥美拉唑对映体分离实验中,其SMB柱分布模式为2-2-2-2。若把I带的一个柱子调整到II带中,其柱分布变为1-3-2-2;若再把IV中的一个柱子调整到III带,其柱分布为1-3-3-1。保持其他参数不变,对调整后的SMB分离结果进行模拟计算,计算结果见表3。
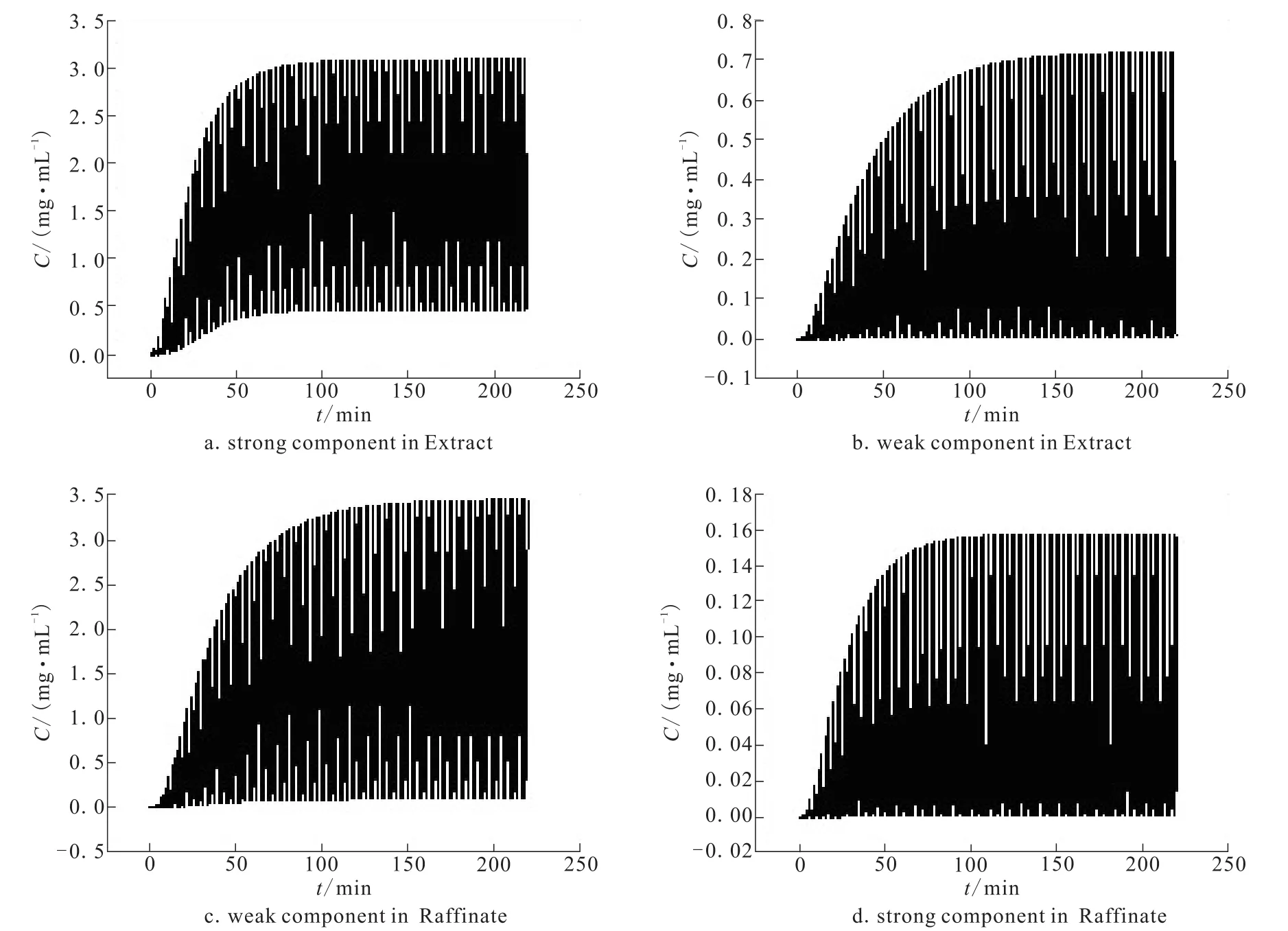
图2 E口和R口洗脱曲线Fig.2 Elution curve of Extract and Raffinate

表3 SMB传统工艺与Varicol工艺模拟结果,%Tab.3 Calculation results of traditional process and Varicol process,%
由表3可知,通过增加II带的柱子个数,E口纯度有所提高;增加III带柱子个数可以使R口纯度提高。不过该方法有一定的局限性,若I带和IV带无多余的柱子,又因操作压力等原因不宜再增加柱子时,该方法则无法使用。此时,可以通过新型的SMB分离工艺提高分离纯度。
4.2 Varicol工艺
Varicol即可变柱数的SMB,是一种新型的SMB分离技术,它通过不同步切换改变各带柱数提高分离效率。在Varicol工艺中,每个带中平均柱数可以不是整数,也可以小于1,与传统工艺相比,Varicol工艺可以更好的优化柱数在各区带的分布。
若提高E口产品纯度,可以在一个切换周期的前一半时间内,柱子分布为2-2-2-2,在后一半时间内为2-3-1-2,则在一个切换周期内其各带平均柱数为2-2.5-1.5-2。按此分离模式结合式(13)进行计算,其结果见表3。
由表3可知,Varicol工艺在总柱数不变的情况下,可以通过增加II带的平均柱子数提高E口的分离纯度,此时由于III带平均柱数的减少而导致R口纯度有所降低。由表3的后两列可知,E口的分离纯度方面,Varicol工艺中稍好于传统的SMB分离工艺,但Varicol工艺II带的平均柱子数只有2.5根,而传统的SMB则拥有3根II带柱子数。因此Varicol工艺能够更好地利用固定相进行分离,具有更高的分离效率。
5 结论
(1)采用显式有限差分法建立了SMB色谱模型迭代求解的差分方程;获得了SMB色谱模型的洗脱曲线。
(2)对奥美拉唑对映体的SMB分离实验进行计算验证,计算结果与实验结果基本吻合,验证了本方法的有效性,可以将其与数学优化算法结合对SMB分离操作进行仿真优化。
(3)通过增加II带和III带的色谱柱数目能够相应的提高E口和R口的分离纯度;与传统SMB相比,Varicol SMB工艺能够充分利用固定相进行分离,具有更好的分离效果。
[1]高尚,林海龙,许克家,等.模拟移动床分离技术及食品行业的应用[J].中国酿造,2014,33(8):15-19.
[2]万红贵,方煜宇,叶慧.模拟移动床技术分离缬氨酸和丙氨酸[J].食品与发酵工业,2005,31(12):50-53.
[3]付道贵,王美玲,简敏,等.浓缩硼-10模拟移动床色谱分离的放大研究[J].现代化工,2015,35(2):136-140.
[4]杨明磊,魏民,胡蓉,等.二甲苯模拟移动床分离过程建模与仿真[J].化工学报,2013,64:4335-4341.
[5]陈韬,陈贤铬,徐俊烨,等.模拟移动床色谱法拆分甲霜灵对映体[J].色谱,2016,34(1):68-73.
[6]吴献东,金晓明,苏宏业.基于NSGA-II的模拟移动床色谱分离过程多目标操作优化[J].化工学报,2007,58(8):2038-2044.
[7]IBALANK T Z,ALAIN V W.Optimization of VARICOL SMB processes using hybrid modeling and nonlinear programming[J].Computers and Chemical Engineering,2014,58:1-10.
[8]危凤,沈波,陈明杰.奥美拉唑对映体的模拟移动床色谱分离过程模拟[J].高校化学工程学报,2005,19(4):45-460.
[9]CHEN Y,DAI W X,LIU X S,et al.Kinetic modeling for chromatographic separation of cytosine monophosphate and uracil monophosphate[J].Korean Journal of Chemical Engineering,2006,23(5):784-788.
[10]JIAO P F,WU J L,ZHOU J W,et al.Mathematical modeling of the competitive sorption dynamics of acetone-butanol-ethanol on KA-I resin in a fixed-bed column[J].Adsorption,2015,21:165-176.
[11]王敏,蔡宇杰,须文波.SMB色谱模型数值计算的时空守恒元解元方法[J].计算机工程与设计,2010,31(2):388-392.
[12]ZHANG Y J,FENG L H ,ANDREAS S M.Accelerating optimization and uncertainty quantification of nonlinear SMB chromatography using reduced-order models[J].Computers and Chemical Engineering,2017,96:237-247.
[13]叶忠建,刘飞.基于隐式差分法的色谱分离过程操作模型研究[J].计算机与应用化学,2012,29(7):839-842.
[14]YOUNG J C,SOON K H,SUNG T C,et al.Chromatographic separation of bupivacaine racemate by mathematical model with competitive langmuir isotherm[J].Korean Journal of Chemical Engineering,2004,21(4):829-835.
[15]SUNG Y M.Optimization study of a batch chromatographic process based on Amberchrom-CG161C adsorbent for separation of valine from a ternary amino acid mixture[J].Korean Journal of Chemical Engineering,2016,33(6):1889-1896.
[16]WANG S Y,GUO M,CONG J X.Facile optimization for chromatographic separation of liquiritin and liquiritigenin[J].Journal of Chromatography A,2013,1281:167-171.
[17]KRISZTIAN H N,FAIR C,KRZYSZTOF K.Martin-Synge algorithm for the solution of equilibrium-dispersive model of liquid chromatography[J].Journal of Chromatography A,2010,1217:8127-8135.
[18]陆金甫,关治.偏微分方程数值解法[M].北京:清华大学出版社,2004:53-54.

