例谈一类不等式恒成立求参数范围的解题策略*

广州市铁一中学(510600) 范选文

广州市绿翠现代实验学校(510220) 唐秋萍

已知不等式恒成立求参数的取值范围,一般有两种基本方法:一是“分离参数法”;二是“构造函数法”.其中“构造函数法”是通法,具有普遍性,但难点往往是由于学生没有选对函数而导致解题失败.所以本文笔者将对”指数与幂函数模型”进行整合的函数不等式求参数范围问题进行探究分析,从而获得解决这一类题目求参数范围的应该如何构造函数.

一、问题提出

题目设函数.当x∈(0,1)时,f(x)＞0,求a的取值范围.

此题是笔者在对尖子生培优课堂中一道训练题,改编于2006年全国卷21题,在训练过程中笔者要求学生不允许用分离参数法求解,只能用构造函数法求解.全班40个学生只有1个学生解得答案,其他学生都是直接求导分析函数,导致只能解出答案的一部分.

二、问题解决

思路一直接利用函数进行分析求解.

解答

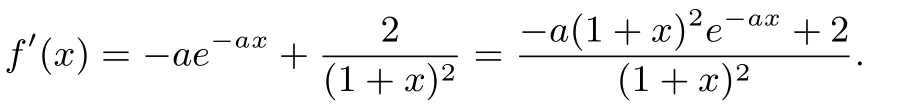
(1)当a≤0时,f′(x)＞0恒成立,所以f(x)在(0,1)上单调递增,则f(x)＞f(0)=0,故a≤0满足题意.

(2)当a＞0时,令g(x)=−a(1+x)2e−ax+2,则

①当a＞2时,g′(x)＞0恒成立,所以g(x)在(0,1)上单调递增,又因为g(0)=−a+2＜0,故在(0,1)区间上存在子区间(0,x0),使得在(0,x0)上g(x)＜0,即在 (0,x0)上f′(x)＜0,则f(x)在 (0,x0)上单调递减,故f(x0)＜f(0)=0,与f(x)＞0矛盾,故a＞2不成立.

②当a=2时,g′(x)＞0恒成立,所以g(x)在(0,1)上单调递增,又因为g(x)＞g(0)=0,即f′(x)＞0恒成立,所以f(x)在(0,1)上单调递增,则f(x)＞f(0)=0,故a=2满足题意.____________

③当1＜a＜2时,令g′(x)=0,解得,所以在上g′(x)＜0,在上g′(x)＞0,故g(x)在上单调递减,在上单调递增.所以

即f′(x)＞0恒成立,所以f(x)在(0,1)上单调递增,则f(x)＞f(0)=0,故1＜a＜2满足题意.

④当0＜a≤1时,g′(x)＜0恒成立,所以g(x)在(0,1)上单调递减,所以g(x)min=g(1)=−4ae−a+2,下面证明g(x)min=−4ae−a+2＞0在a∈(0,1]上恒成立.

即f′(x)＞0恒成立,所以f(x)在(0,1)上单调递增,则f(x)＞f(0)=0,故0＜a≤1满足题意.

综上可得,a的取值范围为(−∞,2].

思路二构造函数h(x)=(1+x)e−ax−(1−x)进行分析求解.

解答

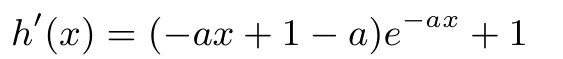
(1)当a≤0时,h′(x)＞0恒成立,所以h(x)在(0,1)上单调递增,则h(x)＞h(0)=0,故a≤0满足题意.

(2)当a＞0时,令g(x)=(−ax+1−a)e−ax+1,则

接下来的讨论过程跟思路一相同,解答过程从略.

思路三构造函数进行分析求解.

解,令g(x)=ax2+2−a.

(1)当a≤0时,g′(x)＞0恒成立,即m′(x)＞0恒成立,所以m(x)在(0,1)上单调递增,则m(x)＞m(0)=0,故a≤0满足题意.

(2)当0＜a≤2时,g′(x)＞0恒成立,即m′(x)＞0恒成立,所以m(x)在(0,1)上单调递增,则m(x)＞m(0)=0,故0＜a≤2满足题意.

(3)当a＞2时,令g(x)=0解得,所以在上m′(x)＜0,在上m′(x)＞0,故

m(x)在上单调递减,在上单调递增.所以恒成立矛盾,故当a＞2时不成立,舍去.

综上(1)(2)(3)可得,a的取值范围为(−∞,2].

评注对于这道题,采用构造不同的函数思路,解答过程完全不一样.思路一和思路二的解答过程非常繁琐,只有思路三的解答过程简单,而且容易理解.因为思路一和思路二的求导函数比较复杂,很难判断和讨论导函数的正负,导致学生在解答过程只停留在第(2)步就做不下去了!思路三的求导函数是我们熟悉的二次函数模型,学生能比较容易去分析和讨论导函数的正负,容易对原函数图象作出详细的分析.

三、解题策略

在遇到“指数与幂函数模型”进行整合的不等式恒成立求参数范围时,则不等式则转换成两类函数相乘(或相除)的模型后再进行构造函数,若遇到“对数与幂函数模型”进行整合的不等式恒成立求参数范围时,则不等式则转换成两类函数相加(或相减)的模型后再进行构造函数,这样只需要一次求导即可得到我们熟悉的函数,学生对参数进行讨论就变得容易.

四、方法运用

例1(2010年全国2卷21题改编)设函数.当x≥0时,f(x)≥0,求a的取值范围.

解显然a≥0,因为若a＜0,则当时,f(x)＜0,与f(x)≥0矛盾.

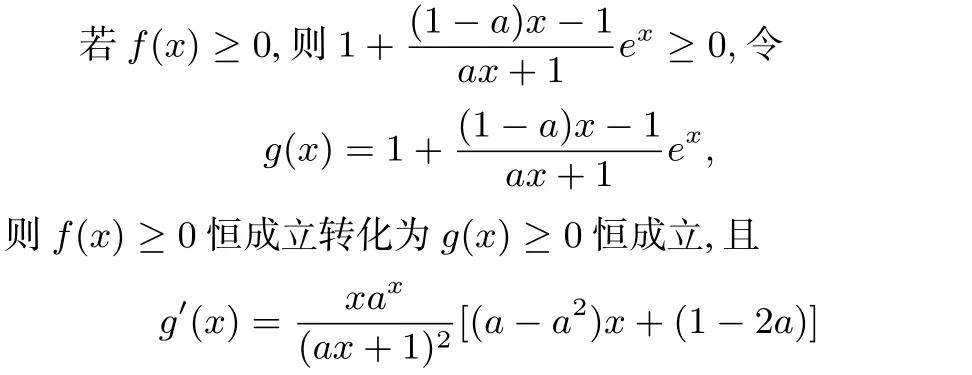
(3)当a≥1时,g′(x)≤0恒成立,所以g(x)在[0,+∞)上单调递减,则g(x)≤g(0)=0,与g(x)≥0矛盾,故a≥1舍去.

综上(1)(2)(3)可得,a的取值范围为.

例2(2011全国新课标卷21题改编)设函数当x＞1时,f(x)＞0,求a的取值范围.

解答,即设,则

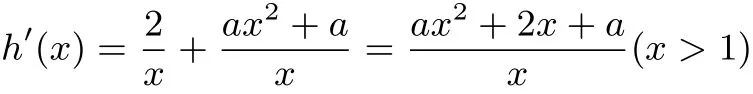
(1)当a≤−1时,在(1,+∞)上,h′(x)≤0,所以h(x)在(1,+∞)上单调递减,所以h(x)＜h(1)=0;

(2)当−1＜a＜0时,令h′(x)=0解得

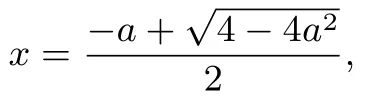
(3)当a≥0时,在(1,+∞)上,h′(x)＞0,所以f(x)在(1,+∞)上单调递增,所以h(x)＞h(1)=0恒成立,这与题意h(x)＜0恒成立矛盾.

综上(1)(2)(3)得,a的取值范围为(−∞,−1].