一种新的基于LPMD的散射路径识别算法

邓 平，芮 洋，邓水发

(西南交通大学信息科学与技术学院，四川成都610097)

在地面无线定位中，因为无线信号传输的固有特性，诸如多径传输、路径损耗、信号间干扰、阴影衰落和非视距传输等因素的影响，都容易导致定位结果偏离真实值.其中，非视距传输是定位误差的主要来源［1-2］.为了在这样的环境中对被测目标进行精确定位，人们研究了很多非视距环境下的定位算法.

其中，基于散射体信息的定位算法，根据研究的方式和方法，主要分为两类:一类就是根据散射体建模，并根据接收信号的统计特征来建立一个数学模型，通过将接收到的信号带入数学模型中进行定位［3-6］;另一类就是根据散射体的几何位置来定位的方法，由于其思路在于把NLOS(non-line-ofsight)误差转化为确定性的物理模型因素，使定位精度主要取决于定位参数的测量精度，和NLOS引起的参数偏差无关，这为实现高精度定位提供了可能，近年来受到了大量的研究和关注［7-12］.

根据统计特征来建模的方法，将所有的视距信号和非视距信号都作为统计信号来处理，并不单独考虑散射信号是单次散射还是多次散射.以上利用散射体的几何位置信息来定位的算法中，绝大部分都没有考虑多次散射路径信号，或者直接假设所有的散射信号都是单次散射路径信号［13-14］，而在非视距干扰严重的环境下，多次散射路径信号的增加会大大降低这些算法的性能.

为了解决散射路径识别的问题，文献［7］提出一种基于LPMD(line-of-possible-mobiledevice)的算法来识别散射信号中的单次散射信号和多次散射信号.该方法先计算各LPMD的到达时间(time-of-arrival，TOA)权值，并通过设定一个门限来筛选一部分权值较小的LPMD，再计算筛选出来的这部分LPMD的几何中心作为参考点的坐标，然后以参考点到各LPMD中点的距离来构造判决计算式.该方法除了最后的散射路径判决外，还多了一次LPMD的TOA权值判决，不仅为参考点的计算带来误差，还没能充分利用所有LPMD的几何信息.而且，直接以各LPMD的几何中心作为参考点的坐标，会使参考点到真实目标之间存在较大的偏差，尤其是当被测目标处于侦测站围成的区域外侧时，这个距离偏差会更大，从而严重影响到最后路径判决的准确度.例如，在边境线、特殊山谷环境和战场环境中，一方面是侦测站选址的限制，一方面是被测目标本身的特性，决定了被测目标基本只会在侦测站围成的区域外侧活动，而这种特殊场景也很少有文献考虑，但其本身依旧具有很大的研究价值，且在近些年来，也鲜有基于LPMD的散射路径识别这类算法的进一步研究.

为此，本文提出了一种新的基于LPMD的识别算法，考虑到普通环境和特殊环境下不同的LPMD的分布特点，以所有LPMD的交点来计算初步参考点位置，并通过对所有交点中，距离初步参考点较远的一部分交点，对剩余的较近的点做负期望补偿来修正参考点的位置.同时使用参考点到各LPMD的直线距离来构造判决计算式.相比文献［7］算法大大优化了参考点的计算准确度，减少了额外的判决次数，无论当被测目标处于侦测站围成区域的内侧或外侧时，都有更优良的散射路径识别性能.

1 LPMD概念

如图1所示，图中:B是侦测站;Dm是被测目标;S是侦测站B接收到的散射信号路径经过的散射点;φ是信号出射角;θ是信号到达角.

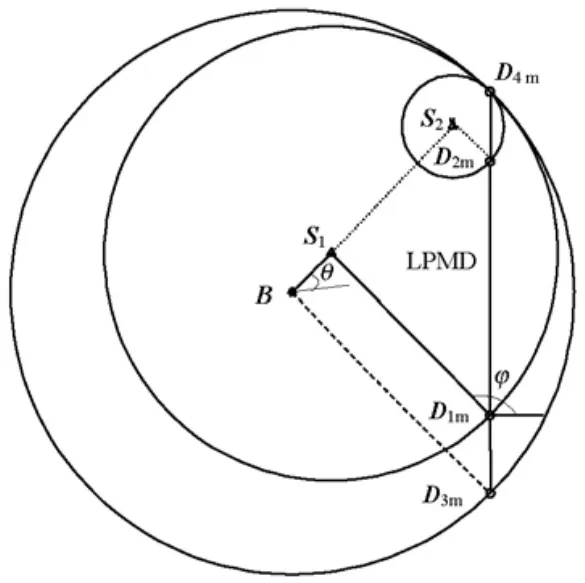
图1 LPMD示意图Fig.1 Sketch map for LPMD

侦测站B在测得接收信号的TOA值和AOA(angle-of-arrival)值后，以TOA测量值的距离为半径画一个大圆，如果目标Dm到侦测站之间是视距传播，则Dm应该在大圆上的一点，此时信号出射角φ和到达角θ应该互补;当然，在非视距环境下，目标到侦测站之间存在NLOS传播，信号经过S的散射之后再到达B，此时，由于信号经过散射的原因，信号出射角φ和到达角θ一般不满足互补.

在NLOS传播情况下，散射体的位置应该在以侦测站B为起点，以信号到达角θ为幅角，幅长小于等于TOA距离的一条线段上;而被测目标Dm在以散射体为圆心的圆上，再加上信号出射角的约束，就可以得到相应的被测目标Dm的位置.

这里讨论的散射信号是单次散射的情况.由图1可以看出，在B看来，S的位置是不固定的，有可能在信号到达角θ这条线段上的任一点，从而Dm的位置也是不固定的，但是B到S的距离dB，S，再加上S到Dm的距离dS，Dm，这个总距离dTOA是固定的.根据式(1)的几何关系

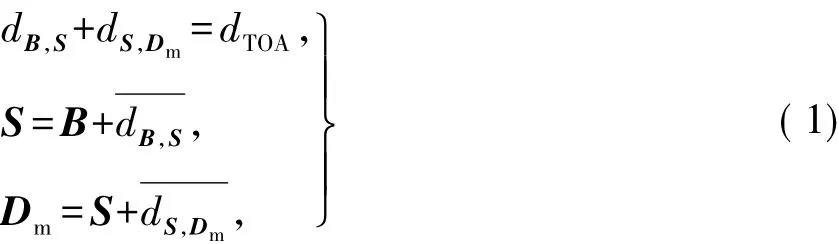
可以在图1中得到Dm所有可能的位置，从而可以发现Dm可能所处的位置是一条线段，这条线段称为Dm的可能位置线，即图1中的LPMD.

2 基于LPMD的识别算法

以上是假设侦测站接收到的信号是单次散射信号，如果考虑到接收到的散射信号中含多次散射信号，由于多次散射信号的TOA值更大，所以其对应的LPMD距离真实目标点更远，从而和单次散射信号的LPMD区分开，如图2所示.

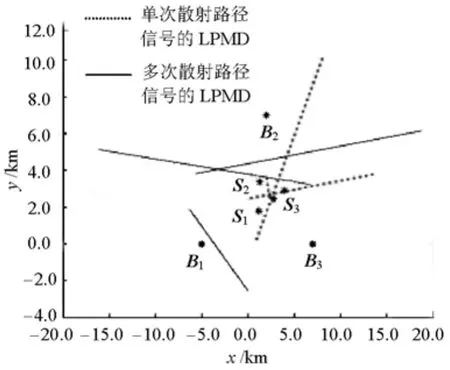
图 2多侦测站LPMD示意Fig.2 Sketch map for LPMDs in multiple stations

图2 中，假设有3个侦测站，真实目标点的坐标为(2.5，2.5)km，在真实目标点周围按照圆环散射模型［15］，半径为1.0 km，随机设了 3个散射点，即图2中的S1、S2、S3，分布在真实目标点的周围，且被测目标的位置在3个侦测站所围成的区域中.目标发射出的信号，一部分经过3个散射体单次散射后被各个侦测站接收，形成单次散射路径;另一部分通过2个或3个散射体的连续多次散射后再被各个侦测站接收，形成多次散射路径.然后依次对各个侦测站按第1节中描述的方法，绘制其对应的LPMD.图2中只画出了部分的单次散射信号的LPMD和部分的多次散射信号的LPMD.从图2可以看出，单次散射路径信号的LPMD相交于真实目标点附近.

对于散射路径的识别，文献［7］中算法分为2个步骤:

步骤1 首先根据各侦测站接收到的散射信号，在坐标轴上得到全部散射信号对应的LPMD图，然后计算其中每条LPMD线的权重，用以计算参考点C，TOA距离越大的权重越小，TOA距离越小的权重越大，计算过程为

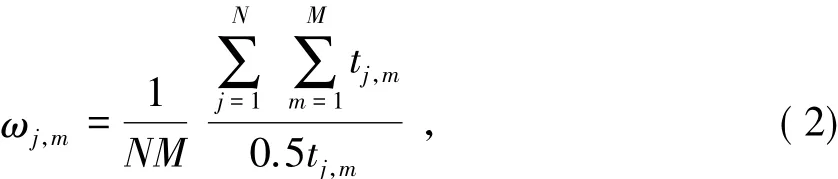
式中:ωj，m为该路径信号对应的权值;M为第j个侦测站的散射信号总数;N为侦测站总数;tj，m为第j个侦测站接收到的第m个散射信号的TOA测量值.

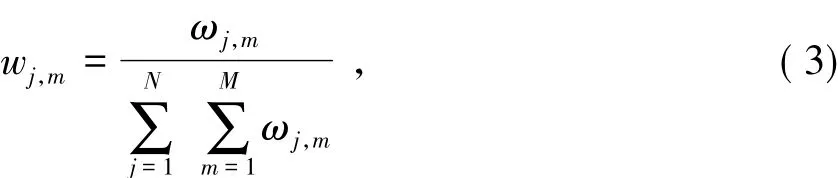
式中:wj，m是第j个侦测站接收到的第m个散射信号对应的权重.

然后设置一个权重门限w，文献［7］中给出的建议值为0.1，只有大于这个门限的LPMD才会被用来计算参考点C，如式(4).

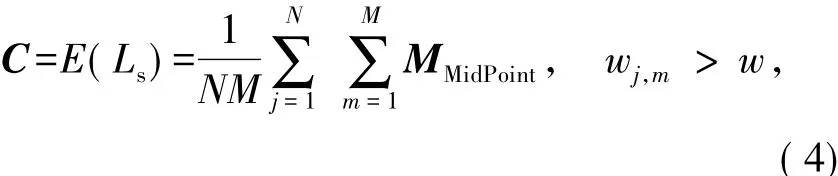
式中:MMidPoint为每条 LPMD的中点坐标;Ls为LPMD总数.

步骤2 得到C的坐标之后，再计算MMidPoint到C的距离权重，文献［7］中以各LPMD的中点到C的距离来构造判决计算式，如式(5).

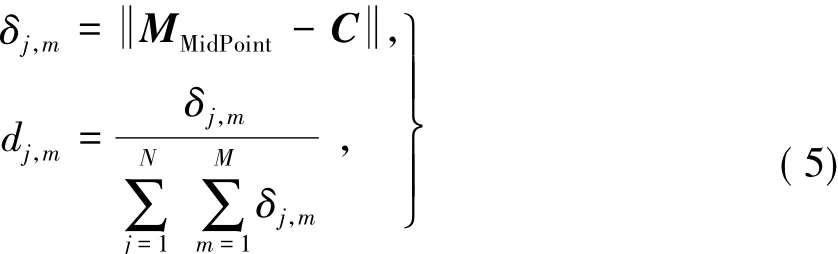
式中:δj，m为第j个侦测站的第m条LPMD到 C的距离权值;dj，m为其对应的距离权重.

这里同样设置一个权重门限d，文献［7］中给出的推荐值是0.2，大于这个门限的LPMD对应的信号路径被判定为多次散射路径，而小于这个门限的LPMD对应的信号路径被判定为单次散射路径，即

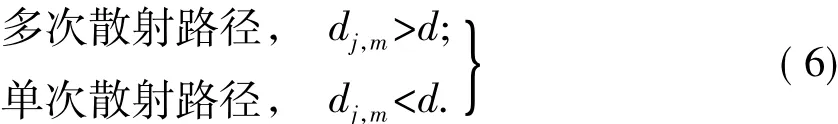
图2中，C即是按式(4)计算的参考点，通过观察可以看出，C到单次散射路径信号的LPMD中点的距离相比到多次散射路径信号的LPMD的距离要短，从而实现对散射路径的识别.

3 本文基于LPMD的识别算法

文献［7］的算法中，总共进行了2次门限判决，而每次判决势必都有误差存在;其次，按文献［7］算法计算的 C，其实是各 LPMD的几何中心，其位置与实际目标点差距较大，会给算法的识别性能带来不利影响;文献［7］算法是针对目标处于侦测站所围成的区域内侧这种情形提出的，并没有考虑目标处于区域外侧的情形.本文中考虑两种情况，(1)普通场景:被测目标处于侦测站围成的区域内侧;(2)特殊场景:被测目标处于侦测站围成的区域外侧.

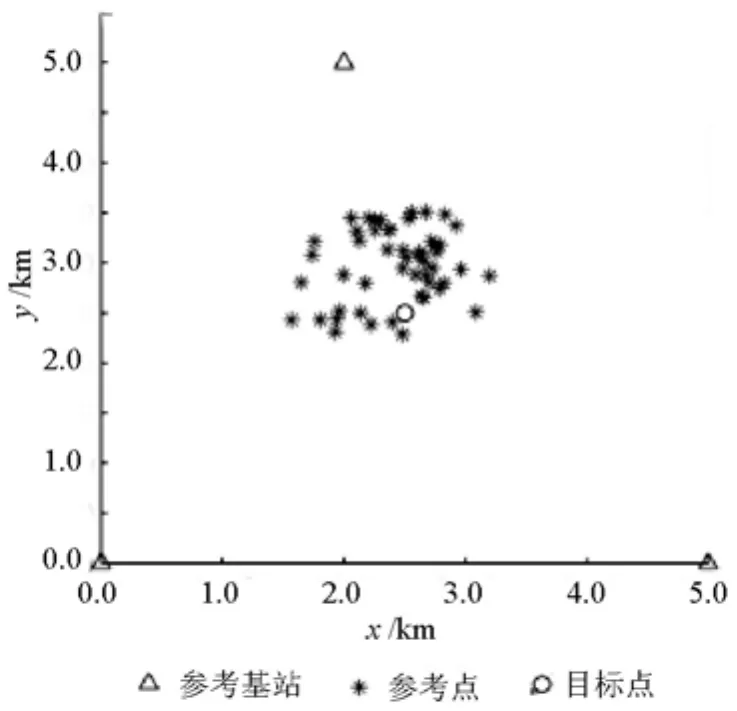
图3 普通场景下文献［7］算法的参考点C位置示意Fig.3 Sketch map for refer-point C of literature［7］under normal scene

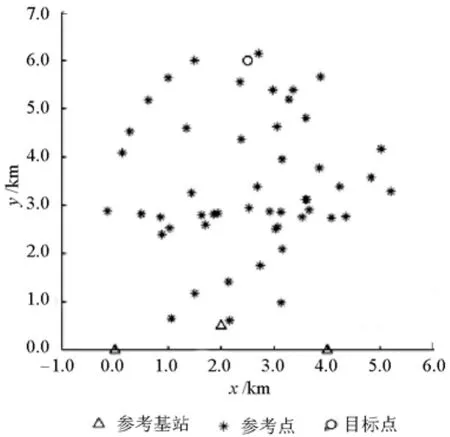
图4 特殊场景下文献［7］算法的参考点C位置示意Fig.4 Sketch map for refer-point C of literature［7］under special scene

图3 和图4分别模拟了50次文献［7］算法在普通和特殊场景下计算的C的位置.通过对比图3和图4可以看出，文献［7］算法在普通场景下，C的位置相对集中在真实目标点周围;而在特殊场景下，C相对真实目标点的偏差，要比普通场景下大很多.

本文在算法设计之初就同时考虑了普通和特殊场景下各自的 LPMD图的特点，采用了和文献［7］算法完全不同的C的计算方式，整个算法分为3步:

第1步 计算所有LPMD的交点Ccrosspoint;

第2步 计算初步参考点并通过负期望补偿来修正;

第3步 通过参考点到LPMD的直线距离来做判决.

首先在计算参考点之前，找出所有LPMD的交点，如图5所示为是单次散射路径信号仿真中的LPMD及其所有交点的计算结果.其中线段为各LPMD，共有49 个交点;目标点位置为(2.5，6.0)km，可以看到，大多数的交点都落在了目标点的附近，只有小部分的交点偏离了很远.这是因为，理想情况下，没有误差等因素影响，单次散射路径信号的LPMD的交点就是目标点的位置，而多次散射路径信号的LPMD会产生离目标点很远的交点.

然后，计算C时，不再使用所有LPMD的两头端点来计算，而是使用所有LPMD的交点来计算，如式(7).

将Ccrosspoint平均之后，得到初步的C的坐标.

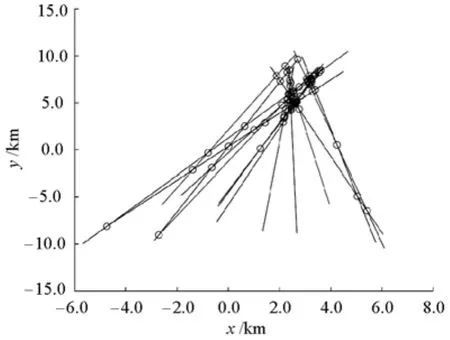
图5 特殊目标环境下的LPMD交点计算示意Fig.5 Sketch map for calculating the cross-points of LPMDs under special scene

由以上分析可知，单次散射路径信号LPMD产生的交点都离目标点相对较近，而多次散射路径信号的LPMD会产生大量的远点，通过取平均来计算参考点时，这些远点把参考点C往其方向拉，从而使计算得出的参考点C偏离目标点较远.尤其是在特殊场景下，如图5所示，LPMD的分布模式大致为扇形放射状，且扇形的头端离目标点很近，但是扇尾部分离目标点很远，这部分的交点在直接做平均的时候，把C从靠近目标点的位置附近拖向了远点方向.所以在计算出初步的参考点之后，应再通过所有交点中的一部分远点对C的位置做负期望补偿，从而对C的位置做修正.

先求出所有交点到修正前C的距离，然后降序排列，取出前Ffixnum个距离最远的点作为优化点，对剩下的Ppointnum－Ffixnum个点做负期望补偿.通过式(8)得到修正后的参考点Ccrt.

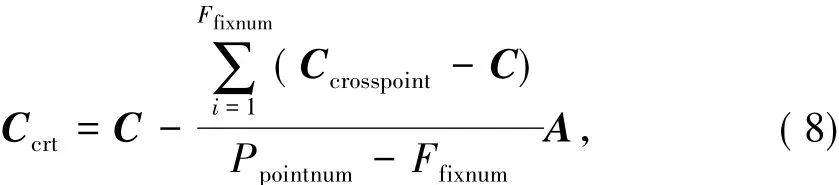
式中:Ppointnum为计算得到的所有交点的个数;Ffixnum占Ppointnum的比例和具体环境的非视距干扰程度有关，干扰越大，多次散射路径信号越多，则Ffixnum需要适当增大，经过仿真测试，建议取值为Ppointnum的1/4，后文的仿真对取值选择进行了说明;A为修正系数矩阵，

式中:Ax和Ay分别为横坐标和纵坐标修正系数，经过仿真测试，建议取值为Ax=Ay=1.1.

得到Ccrt之后，计算Ccrt到每条LPMD的距离权重为

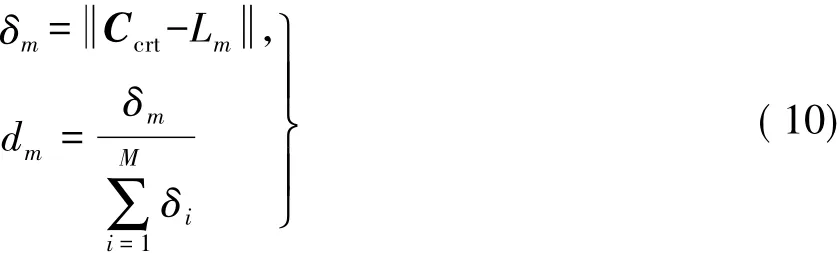
式中:δm为以第m条LPMD到Ccrt的距离权值;dm为其对应的距离权重;Lm为第m条LPMD.

然后设置一个权重门限d，大于该门限的判决为多次散射路径，小于该门限的判决为单次散射路径，即

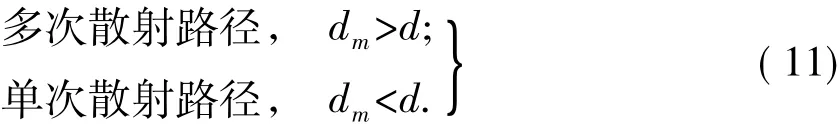
经过仿真测试，推荐 d=0.025.

上述各参数取值虽然是经过仿真给出的建议值，但是相应的值都是在经过对各种复杂的、具有代表性的非视距情景仿真之后，综合各种情景下算法性能得到的具有普适性的值.

在算法复杂度上，相比文献［7］的算法，在得到各侦测站的LPMD之后，本文算法是先计算所有的LPMD的交点，而文献［7］算法是先计算各LPMD的TOA权重，在路径数比较多的情况下，本文算法计算交点的计算复杂度会略高一些，在路径数比较少的情况下，两者计算复杂度相差不大.

4 仿真结果与分析

本文采用圆环散射模型来模拟散射体，散射体个数为3个，随机按散射半径分布在目标点周围;TOA误差为符合N(0，1)分布的加性高斯噪声，AOA误差为符合N(0，π/180)分布的加性高斯噪声，侦测站为3个，单次散射路径为信号从目标点经过1个散射点散射之后分别到达3个侦测站，共有9条单次散射路径;多次散射路径为信号从目标点经过3个散射点中的随机2个和3个点连续散射之后到达侦测站，每个侦测站接收2条，共6条多次散射路径，总共15条散射路径，且不考虑LOS路径，每次仿真独立运行1 000次.分别对普通场景和特殊场景进行仿真，将本文提出的算法与文献［7］中的算法进行比较，并通过仿真对本文算法中的参数选取进行说明.

仿真1 普通场景下，目标点的位置坐标为(2.5，2.5)km，侦测站的位置坐标分别为(0，0)、(2.0，5.0)、(5.0，0)km.散射模型半径为 0.7 km.

通过表1可以得出，普通场景下，本文算法计算的C相对目标点的偏差和文献［7］算法相比，有明显的改进.

表1 普通场景下两种算法的参考点平均偏差Tab.1 Average deviation between refer-point and real target of both algorithms under normal scene

图6中显示了不同散射半径时，两种算法的识别性能对比，可以看出，本文算法不管是漏警概率还是虚警概率，都明显好于文献［7］算法.随着散射半径的增加，两种算法的识别性能提高，这是因为散射半径越大，圆环模型中的3个散射体相互之间的距离也就更远，从而单次散射信号的TOA值和多次散射信号相比，会有更明显的差异，从而更容易识别.

仿真2 特殊场景下，目标点位置为坐标(2.5，6.0)km，侦测站的位置为(0，0)、(2.0，0.5)、(4.0，0)km.散射模型半径为 1.5 km.

通过表2和表1的比较可以得出，特殊场景下文献［7］算法计算得出的参考点位置偏离真实点很大，比普通场景下的偏差更明显，和图4得到的结果基本一致.而本文算法的偏差只是文献［7］算法的 6.67%.

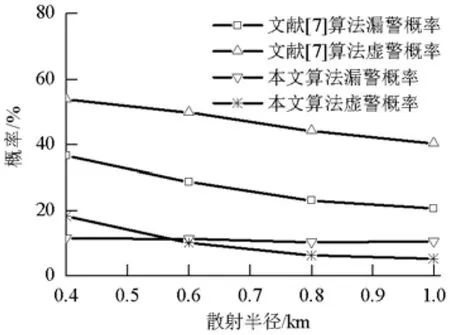
图6 普通场景下不同散射半径时两种算法的识别性能Fig.6 Recognition performance of both algorithms with different scatter radius in normal scenes

表2 特殊场景下两种算法的参考点平均偏差Tab.2 Average deviation between refer-point and real target of both algorithms under special scene

通过图7和图6比较可以得出，随着散射半径的增加，特殊场景也和普通场景一样，两种算法的识别性能都会增加.同时，本文算法的识别性能依旧要明显好于文献［7］算法的.

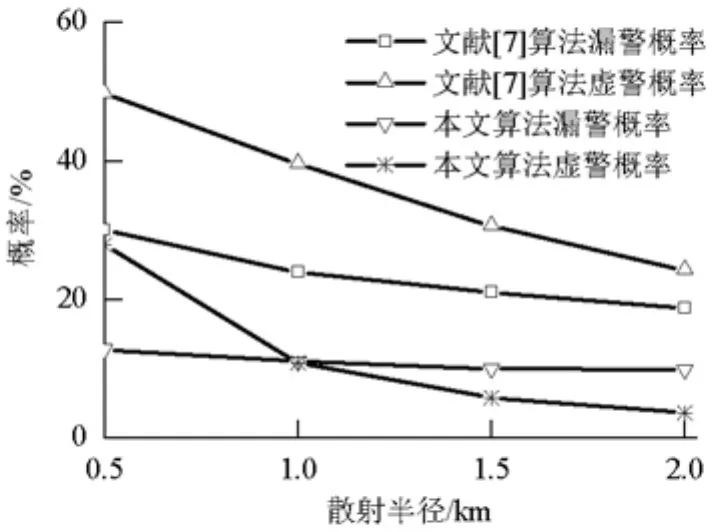
图7 特殊场景下不同散射半径时两种算法的识别性能Fig.7 Recog n ition performance of both algorithms with different scatter radius in special scenes

在图8中，保持散射半径为1.5 km不变，改变目标点的y轴坐标，相当于改变了侦测站和目标点之间的距离.从图8中可以看出，当距离增加时，两种算法的识别性能都变差，但是即使侦测站和目标点之间的距离到了8.0 km，本文算法依旧可以把漏警和虚警概率保持在10%以内.

仿真3 对本文算法中参数Ffixnum的占比情况进行仿真测试，普通场景与仿真1中的场景设置相同，特殊场景与仿真2中的设置相同.为了说明Ffixnum占比取值是如何选出的，先设定其他参数变量:补偿系数 Ax和 Ay设置为1，门限 d参考文献［7］中的取值为 0.2，改变 Ffixnum占 Ppointnum的比例，每次仿真独立运行1 000次，分析算法在不同占比情况下的识别性能.

图9所示仿真结果显示了不同Ffixnum占Ppointnum比例情况下，本文算法的识别性能.从图9中可以看出，在两种场景下，当 Ffixnum占比数为0.25时本文算法具有最小的漏警概率，当比例取0.25时对应最好的识别性能，故上述研究中选择0.25 作为 Ffixnum占 Ppointnum的比值.

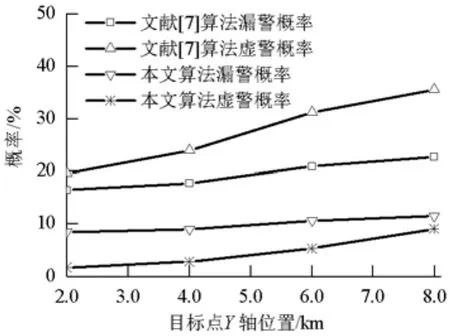
图8 特殊场景下不同目标点距离时两种算法的识别性能Fig.8 Recog n ition performance of both algorithms for different target point distance in special scene

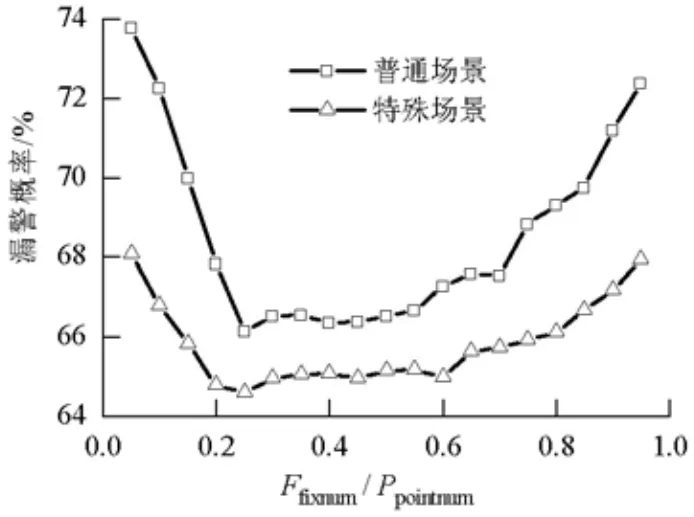
图9 两种场景下不同的识别性能Fig.9 Recognition performance of the new algorithm with different percent of in two scenes

5 结 论

本文提出了一种新的基于LPMD的散射路径识别算法，以所有LPMD交点为基础来计算参考点坐标，并通过负期望补偿来修正参考点的精度，总共只有一次判决，相比文献［7］算法减少了1次额外判决，并且大幅优化了参考点的准确性，不论被测目标处于侦测站围成的区域内侧或外侧时，都能有很好的识别准确度，兼顾普通场景和特殊场景下的识别性能，增加了算法的普适性，在算法的计算复杂度上并没有明显的增加，仿真结果也验证了该方法针对NLOS环境单次、多次散射路径识别问题是有效的.

［1］ JATIVA E R，SANCHEZ D，VIDAL J.NLOS mitigation based on TOA for mobile subscriber positioning systems by weighting measures and geometrical restrictions［C］∥ 2015 Asia-Pacific Conference on Computer Aided System Engineering(APCASE).［S.l.］:IEEE，2015:325-330.

［2］ SILVENTOINEN MI， RANTALAINENT.Mobile station emergency locating in GSM［C］∥ IEEE International Conference on Personal Wireless Communications.［S.l.］:IEEE Xplore，1996:232-238.

［3］ 周非，陈庭盈，范馨月.基于 AOA-TOA重构的单站定位算法［J］.重庆邮电大学学报，2012，24(2):222-226.ZHOU Fei，CHEN Tingying，FAN Xinyue.Algorithm of single station location based on AOA- TOA reconstruction［J］.Journal of Chongqing University of Posts＆ Telecommunications，2012，24(2):222-226.

［4］ TIAN Z，YAO L，ZHOU M，et al.Scattering model based hybrid TOA/AOA/AOD localization in NLOS environment［C］∥ The Proceedingsofthe Second International Conference on Communications，Signal Processing，and Systems.［S.l.］:Springer International Publishing，2014:893-901.

［5］ LIBERTI J C，RAPPAPORT T S.A geometrically based model for line-of-sight multipath radio channels［C］∥Vehicular Technology Conference on Mobile Technology for the Human Race.［S.l.］:IEEE，1996:844-848.

［6］ SIMSIM M T，KHAN N M，RAMER R，et al.Time of arrival statistics in cellular environments［C］∥Proceedings of the 64th IEEE Vehicular Technology Conference.［S.l.］:IEEE，2006:2666-2670.

［7］ SEOW C K，TAN S Y.Non-line-of-sight localization in multipath environments［J］.IEEE Transactions on Moblie Computing，2008，7(5):647-660.

［8］ 杨天池，程娟，邵奇峰，等.单站定位中的散射体位置及散射距离的估计方法:合成运动的扩展卡尔曼估计［J］.电子学报，2014，42(4):730-735.YANF Tianchi，CHENG Juan，SHAO Qifeng，et al.The estimation of the scatterer position and scattering distance in the single station location: the EKF estimation based on synthetic motion［J］. Acta Electronica Sinica，2014，42(4):730-735.

［9］ ZHOU F，FAN X，CHEN T Y.Improved positioning algorithm based on linear constraints on scatterers［J］.EURASIP Journal on Wireless Communications and Networking，2013，2013(1):1-10.

［10］ CHEN S W，SEOW C K，TAN S Y.Virtual reference device- based NLOS localization in multipath environment［J］. IEEE Antennas and Wireless Propagation Letters，2014，13(13):1409-1412.

［11］ ZHU X，SHI M，ZHANG J，et al.A scattering model based non-line-of-sight error mitigating algorithm via distributed multi- antenna［C］∥ IEEE 18th International Symposium on Personal，Indoorand Mobile Radio Communications.［S.l.］:IEEE Xplore，2007:1-5.

［12］ AL-JAZZAR S，GHOGHO M，MCLERNON D.A joint TOA/AOA constrained minimization method for locating wireless devices in non-line-of- sight environment［J］. IEEE Transactionson Vehicular Technology，2009，58(1):468-472.

［13］ 肖竹，陈杰，王东，等.严重遮挡非视距环境下的三维定位方法［J］.通信学报，2015，36(8):68-75.XIAO Zhu，CHEN Jie，WANG Dong，et al.Threedimensionallocalization underseverely obstructed NLOS environment［J］.Journal on Communications，2015，36(8):68-75.

［14］ MIAO H，YU K，JUNTTI M J.Positioning for NLOS propagation:algorithm derivations and cramer-rao bounds［J］. IEEE Transactions on Vehicular Technology，2007，56(5):2568-2580.

［15］ OLENKO A Y，WONG K T，NG H O.Analytically derived TOA- DOA statisticsofuplink/downlink wireless multipaths arisen from scatterers on a hollowdisc around themobile［J］.IEEE Antennasand Wireless Propagation Letters，2003，2(1):345-348.