城市地铁-公交复合网络抗毁性与级联失效仿真

沈 犁， 张殿业，向 阳，王周全，张 桐

(西南交通大学交通运输与物流学院，四川成都610031)

随着我国社会经济发展的飞跃以及城市人口用地规模的突增，为弥补原有公共交通系统的不足，国内各大城市均已逐步加快以地铁为主的城市轨道交通的规划建设.地铁线路所构成的子系统网络与地面公交子系统网络相互关联构成了规模巨大的新型城市公共交通复合系统，其作为一个开放式的复杂系统，是一种基于而又高于现实网络的超网络.由于城市交通网络的庞杂性，国内外许多学者将复杂网络理论［1-19］应用于其网络特性的研究中，而复杂网络本质上的非同质拓扑结构，决定了交通网络中各节点与链路具有不同的重要性.当网络中某关键节点或链路出现故障时，可能会引致整个网络中大量节点的相继失效(级联失效现象)，从而对出行者的出行效率产生严重影响.因此，衡量复合交通网络抗毁性以及级联失效传播性的重要理论意义与应用价值已日益凸显.Albert等［1-2］首先提出了网络受袭后被破坏程度的度量方式;Holme等［3］分析了不同袭击策略下不同网络的受袭结构变化情况;Latora、Seaton等［4-5］对波士顿、维也纳等城市地铁的网络特性进行了研究;Sienkiewicz等［6］对波兰22个城市的公交网络结构进行了指标分析;Motter、Zhao、Cmcitti等［7-10］均先后针对网络的级联失效(cascading failure)做了相关分析，从网络负荷容量及动态演化增长等多方面进行了模型假设与参数分析;高洁等［11］基于客流出行的起终点(origin＆destination，OD)建立了城市轨道交通网络的抗毁可靠性测度指标体系;张建华等［12］对世界城市轨道交通网络的普适性与特殊性进行了研究，基于拓扑与功能两方面脆弱性评价了城市轨道交通复杂网络;殴雯［13］依据恐怖袭击特点分析了在不同攻击模式下的城市轨道交通网络抗毁性能变化趋势;汪涛等［14］以北京、上海、南京、杭州的城市公交系统为研究对象，对各网络在不同攻击模式下的抗毁性进行了分析;陈静、范文礼等［15-16］均探讨了复杂网络节点重要度的评估方法;谢丰等［17］针对ER、BA等3种网络模型在不同袭击策略下的抗毁性进行了仿真分析;窦炳琳、陈世明等［18-19］均提出了改进的网络负载容量非线性模型以有效抵御级联失效.但上述国内外研究多集中于地铁或地面公交网络的抗毁性研究，对级联失效的仿真分析也仅止于单一基础网络，极少有文献涉及对轨道交通与地面公交所构成的城市公共交通复合网络做特性研究.

因此，本文运用复杂网络理论，以成都市为例，构建了城市公共交通复合系统网络，在简要分析网络拓扑结构特性的基础上，首先考察地铁-公交复合网络在不同袭击模式下的静态抗毁性，其后分析突发性事故下地铁客流拥堵的传播扩散现象，从而为城市交通复合网络应对网络受袭失效现象的规划与管理提供一定的理论依据.

1 地铁-公交复合网络模型构建

1.1 模型基本假设

首先在构建城市地铁-公交复合网络时，鉴于站点的普遍对称性，提出以下假设:

(1)进行恐怖袭击下地铁-公交复合网络的抗毁性研究时，由于袭击通常会作用于某些网络节点或连边致其失效，若考虑受袭后网络中实际的客流流向，其通常并不会在节点或连边失效后继续通过公共交通方式进行疏散.因此此处构建无向非加权网络.

(2)为构建无向网络，首先将地铁站点与常规公交站点作为复合网络节点，考虑部分近邻公交站点的重复性，对相距100 m内的重名站点进行合并处理;其次，考虑线路站点的对称性，对上下行的线路与站点进行合并处理.在对线路相邻站点进行连接时，也对两种交通方式的衔接站点做连边处理，即当地铁车站周边500 m范围内有公交站台时，则视作此地铁节点与此部分公交节点间均有连接边.由此构建非加权网络.

(3)进行拥堵失效下地铁-公交复合网络的级联传播性研究时，鉴于地铁线路与公交线路在运能方面具有极大差距，此处考虑非常态下由于高峰时段(1 h)地铁站点拥堵所引起的级联失效现象，即主要由于突发性安全事故引致地铁站点或连边失效而形成的拥堵传播现象.由于级联失效是一种负载网络中的某些节点由正常态转为失效态后可能导致其他节点接连失效的扩散现象，此处构建有向加权网络.

(4)为构建有向网络，除同样对地铁站点与常规公交站点做上述连接处理外，还分别将各站点间的上下行线路作为节点对间的两条反向连边.同时，为构建加权网络，需要考虑网络各连边的容量限制情况:对于同质节点(同方式)之间的连边，其最大容量为两站间线路高峰小时的最大输送能力;对于异质节点(不同方式)之间的连边，由于其代表连接关系而不具有明确的通行能力限制，此处不施加容量限制.鉴于公交节点的乘客容纳能力并不仅限于站台，因此不对其节点容量加以限制.对于地铁节点，虽然其站点实际具有容量限制，但由于主要制约其能力的关键在于地铁线路的输送能力，因此仅将其视为中转集结点，同样不设立容量限制.本文主要以《成都市城市快速轨道交通建设规划(2012～2017 年)客流预测研究报告》［20］(西南交通大学提供)中2020年的地铁客流预测数据为基础进行仿真分析，设定网络中各地铁连边的初始权重为高峰小时地铁站间的客流断面值，复合网络连边的分配流量均不能超过其最大负载容量.

1.2 网络模型构建

鉴于上述假设，本文以成都市为例，依据成都市城市轨道交通近期建设规划(图 1，2012～2020年，成都地铁有限责任公司提供)与截至2015年6月的成都市二圈层范围内的常规公交线网(通过成都市公交集团线路信息系统采集)(图2)，通过剔除部分孤立线路与节点，构建了全连通的地铁-公交复合网络，其中地铁网络由8条地铁线路共190个地铁站点构成，常规公交网络由312条常规公交线路共3 783个公交站点构成，地铁-公交复合网络共由320条线路共3 973个站点构成.城市地铁-公交复合网络为

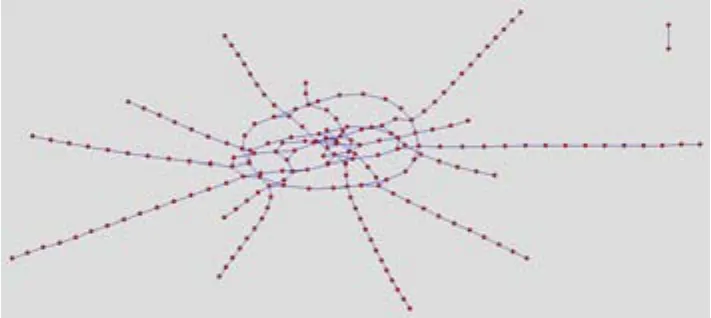
图1 成都市地铁网络拓扑结构示意图Fig.1 Topological diagram of Chengdu subway networks

式中:

V={v1，v2，…，vN}为复合网络 G 的节点集，网络节点总数N=3 973，其中:v1～v190为地铁站点，v191～v3973为常规公交站点;

E={e1，e2，…，eM}为复合网络 G 的连边集，代表各地铁、常规公交线路行经的站点对间路段;

W={ws，ts，t∈V}为连边负载流量集.

图2 成都市地铁-公交复合网络拓扑结构示意图Fig.2 Topological diagram of Chengdu subway-bus compound networks

2 恐怖袭击下复合网络的静态抗毁性

2.1 抗毁性测度模型

此处不考虑由于负载重分配而引起的级联失效现象，仅构建复合网络的无向非加权连通图G=(V，E).鉴于复合网络规模庞大，此处主要选用最大连通度与网络效率来作为复合网络在恐怖袭击下的抗毁性测度.

(1)最大连通度

当遭受连续袭击时，复合网络的总体连通性为衡量其抗毁性的一项重要指标，而最大连通度测度可以较好地描述网络中各节点的连通程度.将图中所有节点用最少的边连接起来的子图定义为最大连通子图，最大连通子图中节点数目与网络中所有节点数目的比值即为最大连通度S，因此有

式中:

n为最大连通子图的节点数目.

最大连通度越大，代表网络节点间连通性越高，网络抗毁性越强.

(2)网络效率

由于通过最大连通子图的平均路径长度难以有效评估网络连通性的实际变化情况，此处采用网络效率测度Eglobal衡量复合网络的抗毁性，其代表网络中OD量均为沿最短路径流通的平均效率.定义网络中两节点vi、vj间的距离dij为其最短路径边

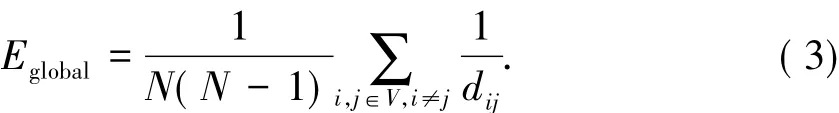
2.2 网络袭击策略

2.2.1 袭击方式

针对网络的静态拓扑结构主要有袭击节点与连边两种方式.鉴于上述网络不具备自我恢复性能的假设，当网络节点受袭时，本文将受袭节点及其相邻连边均予以删除，而当连边受袭时，仅对该连边做删除处理.

2.2.2 袭击类型

主要考虑两种极端情况下的袭击类型:

(1)未获取信息的连续随机袭击.此时袭击者仅能采取盲目袭击，即完全随机地删除网络中一定比例的节点或连边.

(2)获取全部信息的连续蓄意袭击.此时袭击者将基于完全信息对网络采取针对性袭击，即首先根据节点或连边的重要度排序，再依次删除一定比例的节点和连边.

2.2.3 袭击策略

鉴于介数能有效反映节点或连边在整个网络中的作用和影响力，此处采用基于介数的袭击策略来分析城市地铁-公交复合网络拓扑结构的抗毁性.网络中不相邻的节点vl、vm间的最短路径会途经某些节点与连边，如果某个节点vi或连边eij被许多条最短路径经过，则其重要性或影响力可用节点介数Bi与连边介数Bij来表征，其定义分别为数，则

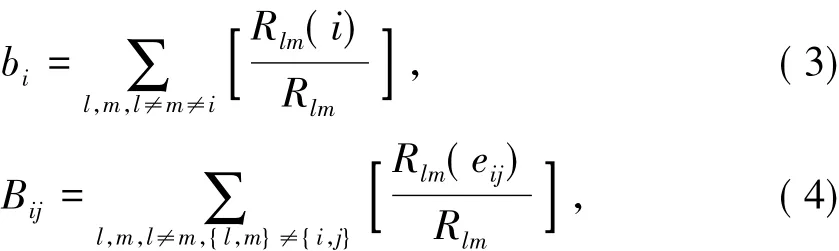
式中:

Rlm为节点vl、vm之间的最短路径条数，其中:Rlm(i)、Rlm(eij)分别为节点vl、vm之间的最短路径经过节点或连边的条数.

节点vi或连边eij的介数即为网络所有最短路径中经过该节点或连边的数量比例.

2.3 抗毁性仿真分析

2.3.1 仿真设计

采用上述构建的成都市地铁-公交复合网络(忽略地铁站点受袭全线停运的情况)，结合网络抗毁性测度，依据网络袭击策略进行仿真分析，实验流程如图3所示.

仿真实验过程如下:

(1)零信息连续随机袭击时，每次删除2.5%的节点或连边，并连续进行10次取平均值;

(2)完全信息连续蓄意袭击时，按照节点或连边介数的序列每次删除2.5%的节点或连边，当遇到多个相同节点或连边介数时，随机选取一个.

2.3.2 仿真分析

(1)零信息连续随机袭击仿真实验

分别针对地铁子网络、地面公交子网络以及地铁-公交复合网络在受到针对节点或连边的零信息连续随机袭击时其最大连通度与网络效率的持续性变化进行分析.由图4可见，在随机袭击下，复合网络最大连通度的下降幅度小于两子网络，而在连边袭击下，相较节点袭击，复合网络最大子图的连通度降速更低.而如图5，地铁-公交复合网络的网络效率变化趋势与地面公交子网络基本一致，同时由于地铁子网络对整个复合网络所起到的支撑性作用，令复合网络的整体效率又高于地面公交子网络.

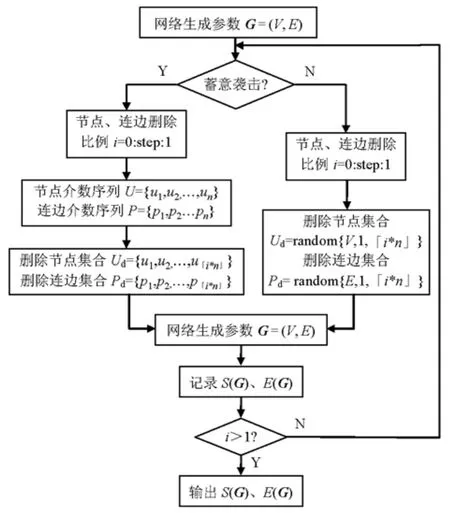
图3 抗毁性仿真实验流程图Fig.3 Flow chart of simulation

(2)完全信息连续蓄意袭击仿真实验

分别针对复合网络及其两子网络在受到针对节点或连边的完全信息连续蓄意袭击时其最大连通度与网络效率的持续性变化进行分析.由图6、7可见，在蓄意袭击下，复合网络的两项指标的变化趋势与地面公交子网络基本保持一致，同时其整体网络指标的下降幅度与速度均低于地面公交子网络.这主要是由于地铁子网络能够在一定程度上串联整合地面公交网络，作为主要脉络对地面公交系统形成有效补充，从而在一定程度上提升复合网络的整体性能.

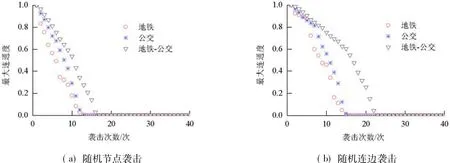
图4 复合网络与子网络最大连通度对比Fig.4 Comparison of maximal connected degree of compound network and its two sub-networks under random attack

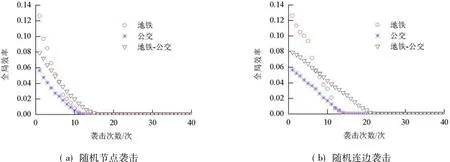
图5 复合网络与子网络全局效率对比Fig.5 Comparison of global efficiency of compound network and its two sub-networks under random attack

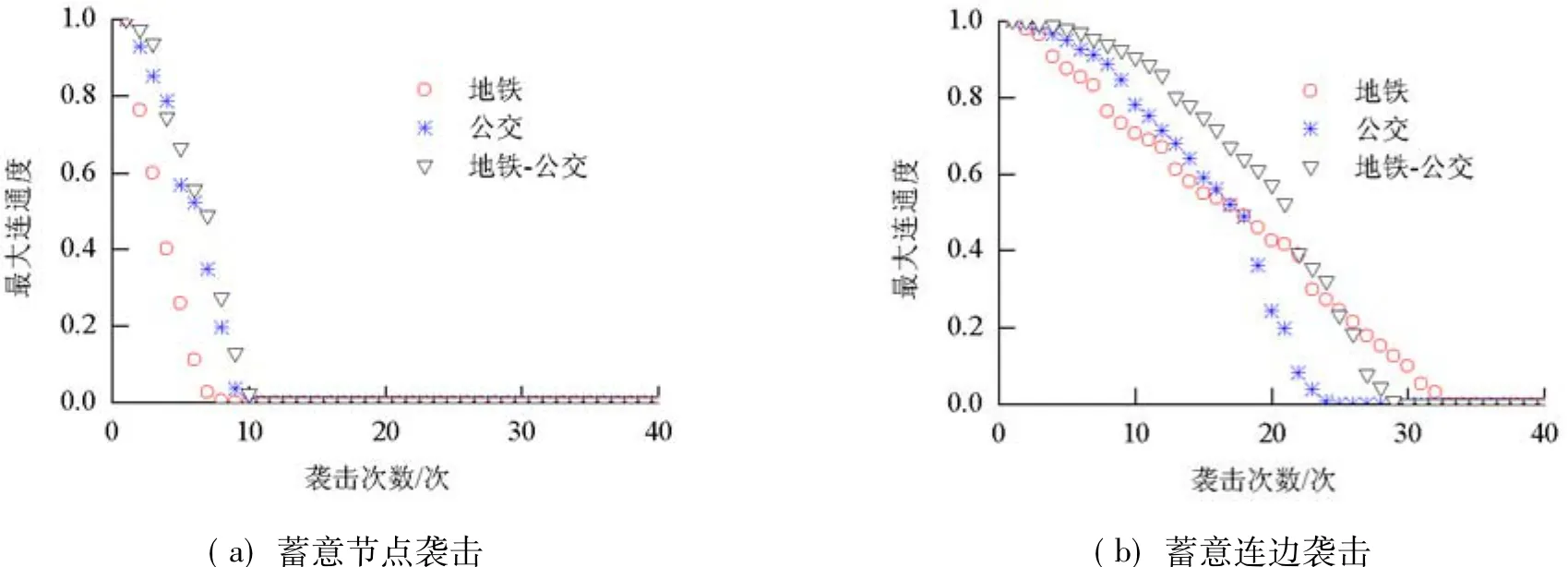
图6 复合网络与子网络最大连通度对比Fig.6 Comparison of maximal connected degree of compound network and its two sub-networks under intentional attack

(3)仿真结论

由仿真分析可以看出，在随机袭击与蓄意袭击两种情况下，地铁-公交复合网络的最大连通度与网络效率的降幅与降速均低于地铁子网络与地面公交子网络.可见相比传统的单一常规公交网络，通过建设轨道交通系统网络以构建城市公共交通新型复合网络能够有效提高网络整体的抗毁性.随着越来越多城市加快轨道交通的建设，以地铁为主的城市轨道系统网络能够在一定程度上增进地铁-公交复合网络的整体效能与抗毁性，轨道交通子系统与地面公交子系统间存在协调发展的必要性与可能性，同时结合上述对网络中关键节点与连边的识别，也有必要研究制定相应的复合网络应急联动机制，以有效应对突发的网络失效现象.

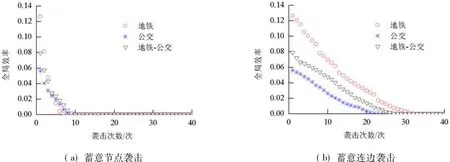
图7 复合网络与子网络全局效率对比Fig.7 Comparison of global efficiency of compound network and its two sub-networks under intentional attack

3 拥堵失效下复合网络的级联传播性

由于城市地铁-公交复合网络实际具有容量限制与客流负载，任意一个节点或一条连边因负载超过最大容量而由正常态变为失效态(过饱和态)后均会引起局部乃至整个网络负载流量的重新分配，这可能会导致网络中其他节点或连边的接连失效，从而令此类失效现象(交通网络中表现为拥堵现象)在网络中逐步传播扩散、产生级联效应，最终可能引致局部甚至整个网络的崩溃，此类现象称为级联失效.在分析复合网络静态拓扑特性的基础上也有必要对负载网络的级联失效现象进行探讨.此处主要考虑非常态下由于早高峰时段(1 h)地铁线路客流拥堵所引起的级联失效现象，即主要由于突发性事故所引起的地铁线路失效在网络中形成的拥堵传播现象.对于以成都市为实例所构建的地铁-公交复合网络，其中地铁1号线至4号线为6B编组，设计运输能力(即在定员情况下地铁的高峰小时单向输送能力)为4.38万(人·次)/h;其他地铁线路均为6A编组，其设计运输能力为5.58万(人·次)/h;对于公交线路能力，依据成都市公交集团公示信息设定高峰发车频率为2 min，基于统一CDK车型(定载89人)的单线单向高峰时段最大输送能力为2 670(人·次)/h.

3.1 突发性安全事故引致地铁拥堵的传播扩散现象研究

突发性安全事故是造成交通拥堵的重要因素.当地铁线路站点或站间出现突发性事故且不能即时处理时，可能导致该线路临时全线停运.若在高峰通勤出行时段，会令大量乘客在沿线各站点滞留且难以疏解，从而出现严重的拥堵现象，影响局部乃至整个城市公共交通网络的正常运作.考虑极端情况下的拥堵扩散情况，即临时停运信息在此时段内未能有效传播，同时地铁站点周边未安排临时公交线路，乘客也未提前选择其他方式出行，仅能以此地铁线路站点为起点在现有网络基础上重新安排出行线路.

此处主要涉及4类矩阵，分别为复合网络的关联矩阵G、复合网络各连边的容量矩阵K、流量矩阵W以及复合网络地铁线路的高峰站间客流OD矩阵O.其中:G为N阶有向关联矩阵;K为依据线路设计能力赋予容量限制的N阶矩阵;W为根据文献［20］中预测的2020年地铁线路高峰小时最大客流断面流量设立的网络中各节点间连边初始权重矩阵;每条地铁线路的高峰站间客流OD矩阵O均源于文献［20］中2020年的客流预测数据.

依次研究8条地铁线路分别因突发性事故引起全线停运时的网络拥堵扩散状况，根据线路OD量以各站点为起讫点重新选择通行路径进行流量分配.具体分析步骤如下:

(1)去除单条停运线路站间连边后，以SPFA［21］找出基于复合网络的该线路节点对间的最短出行路径，依据线路OD量在不考虑最大容量限制的情况下对出行路径所经过的连边赋予客流权重.其后将每条连边上的流量值除以其最大容量，即得到各连边的超负荷系数.当超负荷系数大于等于1时代表其处于失效态，将失效连边除以网络总连边数，即得到网络的失效度.通过失效连边的平均超负荷系数及网络失效度即可适当表述复合网络拥堵传播的强度与广度;

(2)由于实际网络各连边的负载流量均不能超过其最大负载容量，因此基于对通勤时间成本的考虑，在乘客无法选择最优路径出行时，其通常会倾向选择次优或其他的通行路径.以此为流量分配原则，同时考虑到客流的时序性，从线路上下行的末端站开始，反向以各地铁站为起点，而依次以后序站点为终点，基于周边各节点连边依序选择各起讫点间的最短路径进行OD量分配.其中每当一条连边上的分配流量达至其最大容量而处于饱和态时，即认为其处于失效态，将其从可选连边集中去除，再重新选择最优路径，直至以首端站为起点将客流量分配完毕.其后分别统计网络中各已选连边的饱和度及处于失效态的连边数目，以评估网络拥堵失效的级联传播与扩散特性.

3.2 仿真实验结果分析

利用Matlab软件对成都市地铁-公交复合网络进行仿真，对于非容量限制下与容量限制下单条地铁线路停运引致的拥堵失效现象，在复合网络中的传播的实验结果如表1与图8、9所示.

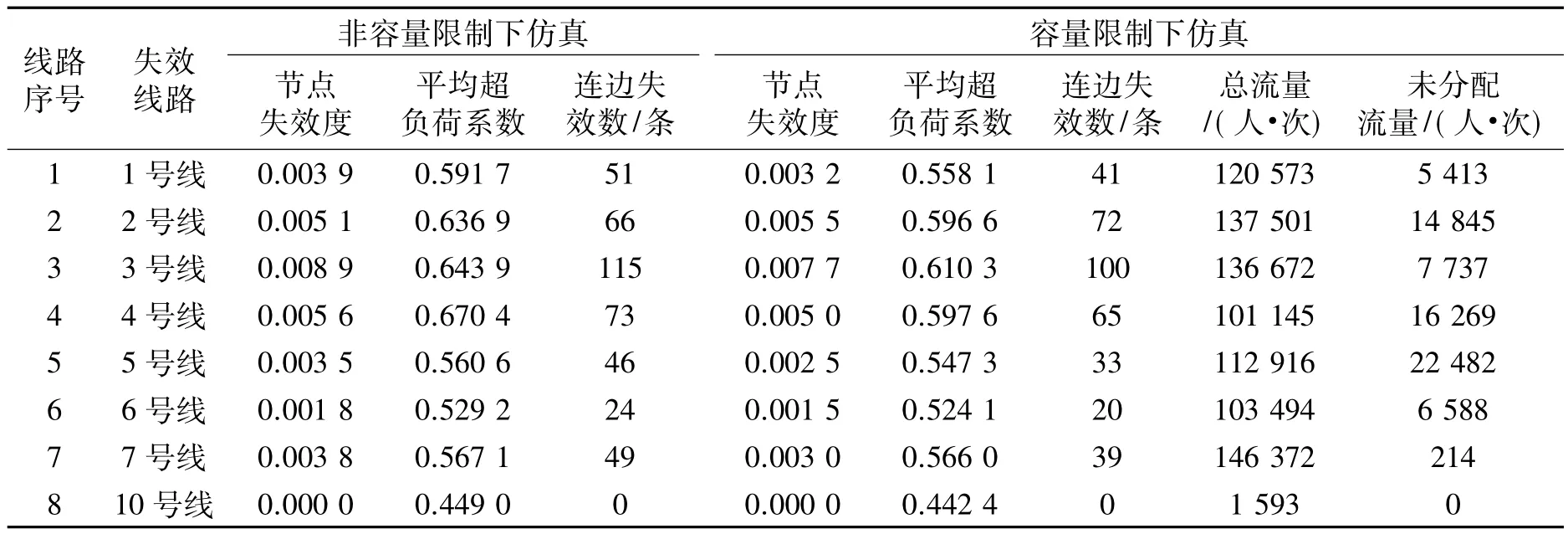
表1 非容量限制下与容量限制下的仿真实验结果Tab.1 Simulation results without＆with restrictive capacity

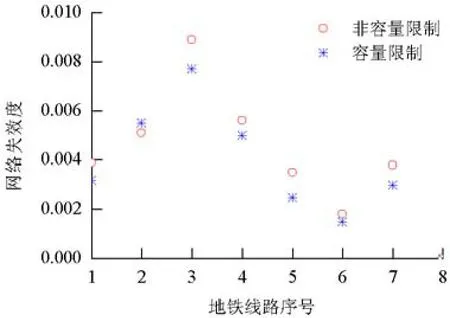
图8 有无容量限制下的网络失效度对比Fig.8 Network failure degree comparison with＆without restrictive capacity

对于非容量限制下的复合网络拥堵失效传播仿真测试，主要可用以评判在不改变既有公交网络的条件下临时加密相关公交线路发车间隔的疏运有效性与必要性.依据不同地铁线路停运所导致的公交失效连边，可在运力资源与道路系统条件允许下，针对性地增加其所属公交线路的临时发车班次，则可有效降低失效公交连边的超负荷系数，以满足轨道滞留乘客的接续出行需求.对于容量限制下的仿真，主要可用以评判在不改变既有公交网络的条件下临时增加应急线路的疏运有效性与必要性，依据未分配完毕的OD流量，同时考虑缓解不同地铁线路停运所导致的公交线路失效连边的客流压力，基于失效轨道站点在其所属的应急接驳区间设置临时公交线路以为各线路的滞留乘客提供应急疏运服务.

由表1可见，在公交容量限制下，如地铁2、4、5号线沿线的既有公交线路对轨道交通突发事件下滞留客流的应急疏运能力较弱，不能完全承担轨道拥堵失效情况下乘客的出行需求，虽然此处主要考虑轨道线路临时全线停运的极端情况，但也有必要针对此类轨道线路可能发生的客流拥堵现象制定相应的公交应急联动预案，为此部分溢出客流提供相应的接续出行服务.因此基于上述两种条件下的测试结果，结合上节对复合网络中各节点与连边重要度的分析，针对不同的线路拥堵失效仿真结果，可将加密既有公交线路发车间隔与增加临时公交线走行两种公交应急联动策略相结合，一方面加强既有公交线路的输送能力以缓解其在分担轨道客流时可能受到的过高负载影响，另一方面在既有公交线路难以对滞留乘客形成有效疏解时通过设置临时公交线路为溢出客流提供高效的疏运服务，同时进一步分担既有公交线路的突增客流压力，起到促进拥堵客流消散的作用.

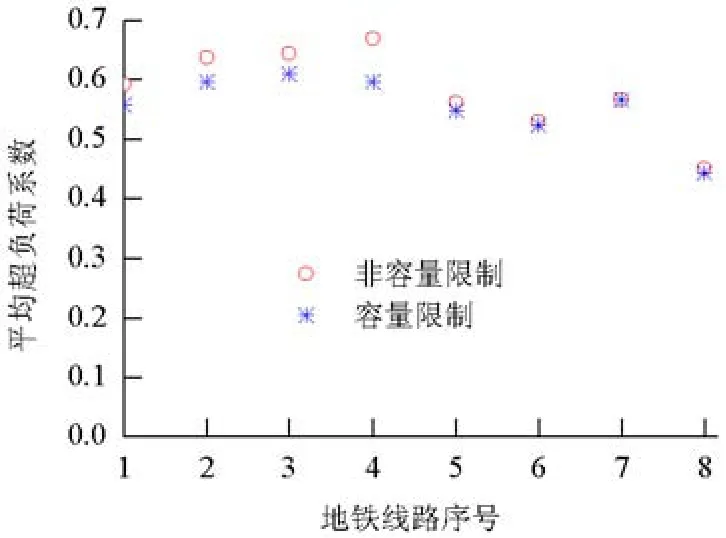
图9 有无容量限制下的平均超负荷系数对比Fig.9 Average overload factor comparison with＆without restrictive capacity

4 结论

主要运用复杂网络理论，以成都市为例构建了城市公共交通复合系统网络，在简要分析其拓扑结构特性的基础上，首先测度了城市地铁-公交复合网络在随机与蓄意两种针对节点或连边的不同袭击模式下的静态抗毁性，其后分析了突发性事故下地铁客流拥堵失效现象在复合网络中的传播扩散性.一方面通过对网络静态抗毁性的测度判断节点与连边的重要度，从而识别关键节点与连边，以针对性加强网络在连续袭击尤其是蓄意袭击下的抗毁性能;另一方面基于对网络负载容量限制条件的设立，通过对地铁线路失效时受阻客流在地铁-公交复合网络中疏解效率的仿真分析，在既有公交线网难以对轨道堵塞客流形成有效疏解条件下，合理设置具有针对性的公交应急联动预案，以有效应对复合网络中客流拥堵引致的级联失效.由此通过对上述复合网络两方面特性的分析探讨，可为城市公共交通复合网络在应对网络受袭与拥堵失效时其规划方案与管理措施的制定提供一定的理论依据.

［1］ ALBERT R，JEONG H，BARABASI A L.Attack and error tolerance in complex networks［J］.Nature，2000，406(6794):387-482.

［2］ ALBERT R，BARAB SI A L.Statistical mechanics of complex networks［J］.Lecture Notes in Physics，2001，74(1):1-54.

［3］ HOLME P，KIM B J，YOON C N，et al.Attack vulnerability of complex networks［J］.Physical Review E Statistical Nonlinear ＆ Soft Matter Physics，2004，65(5):634-643.

［4］ LATORA V，MARCHIORI M.Is the Boston subway a small world network? ［J］.Physical A，2002，314(1/2/3/4):109-113.

［5］ SEATON K A，HACKETT L M.Stations，trains and small world networks［J］.Physical A，2004，339(3/4):635-644.

［6］ SIENKIEWIEZ J，HOLYST J A.Statistical analysis of 22 public transport networks in Poland［J］.Physical Review E Statistical Nonlinear＆ Soft Matter Physics，2005，72(4):046127/1-046127/11.

［7］ MOTTER A E.Cascade control and defense in complex networks［J］.Physical Review Letters，2004，93(9):098701/1-098701/4.

［8］ ZHAO L，PARK K，LAI Y C.Attack vulnerability of scale-free networks due to cascading breakdown［J］.Physical Review E Statistical Nonlinear＆Soft Matter Physics，2004，70(3):035101/1-035101/4.

［9］ ZHAO L，PARK K，LAI Y C，et al.Tolerance of scalefree networks against attack-induced cascades［J］.Physical Review E Statistical Nonlinear＆Soft Matter Physics，2005，72(2):986-1023.

［10］ CRUCITTI P，LATORA V，MARCHIORI M.Model for cascading failures in complex networks［J］.Physical Review E Statistical Nonlinear＆Soft Matter Physics，2004，69(2):266-289.

［11］ 高洁，施其洲.城市轨道网络抗毁可靠性定义及评价指标模型研究［J］.铁道学报，2007，29(3):29-33.GAO Jie， SHI Qizhou.Definition and evaluation modeling of metro network invulnerability［J］.Journal of the China Railway Society，2007，29(3):29-33.

［12］ ZHANG J H，XU X M，HONG L，et al.Networked analysis of the Shanghai subway network in China［J］.Physica A:Statistical Mechanics＆its Applications，2011，390(23):4562-4570.

［13］ 欧雯.恐怖袭击下城市轨道交通网络抗毁性分析［D］.成都:西南交通大学，2014.

［14］ 汪涛，吴琳丽.基于复杂网络的城市公交网络抗毁性分析［J］.计算机应用研究，2010，27(11):4084-4086.WANG Tao，WU Linli.Research on invulnerability of urban transit network based on complex network［J］.Application Research of Computers，2010，27(11):4084-4086.

［15］ 陈静，孙林夫.复杂网络中节点重要度评估［J］.西南交通大学学报，2009，44(3):426-429.CHEN Jing，SUN Linfu.Evaluation of node importance in complex networks［J］.Journal of Southwest Jiaotong University，2009，44(3):426-429.

［16］ 范文礼，刘志刚.基于传输效率矩阵的复杂网络节点重要度排序方法［J］.西南交通大学学报，2014，49(2):337-342.FAN Wenli，LIU Zhigang.Ranking method for node importance based on efficiency matrix［J］.Journal of Southwest Jiaotong University，2014，49(2):337-342.

［17］ 谢丰，程苏琦，陈冬青，等.基于级联失效的复杂网络抗毁性［J］.清华大学学报:自然科学版，2011，51(10):1252-1257.XIE Feng，CHENG Suqi，CHEN Dongqing，et al.Cascade- based attack vulnerability in complex networks［J］. Journal of Tsinghua University:Sci＆ Tech，2011，51(10):1252-1257.

［18］ 窦炳琳，张世永.复杂网络上级联失效的负载容量模型［J］.系统仿真学报，2011(7):1459-1463.DOU Binglin，ZHANG Shiyong.Load-capacity model for cascading failures of complex networks［J］.Journal of System Simulation，2011(7):1459-1463.

［19］ 陈世明，庞少鹏，邹小群，等.面向级联失效的加权网络负载容量非线性模型鲁棒性优化［J］.控制与决策，2013，28(7):1041-1045.CHEN Shiming，PANG Shaopeng，ZOU Xiaoqun，et al.Robustness optimization ofload- capacity nonlinear model in weighted network for cascading failure［J］.Control and Decision，2013，28(7):1041-1045.

［20］ 金键，梅丽，周家中，等.成都市城市快速轨道交通建设规划(2012—2017)客流预测研究［R］.成都:西南交通大学，2011.

［21］ 段凡丁.关于最短路径的SPFA快速算法［J］.西南交通大学学报，1994，29(2):207-212.DUAN Fanding.A faster algorithm for shortest-path SPFA［J］.Journal of Southwest Jiaotong University，1994，29(2):207-212.