移动荷载下含纵横向双裂纹沥青路面复合断裂特性
艾长发, 徐 铖, 任东亚, 郭玉金, 阳恩慧
(1.西南交通大学土木工程学院,四川成都610031;2.西南交通大学道路工程四川省重点实验室,四川成都610031)
路表轮迹带处纵向top-down及裂纹基层反射裂纹是半刚性基层沥青路面初始开裂的主要形式,该类开裂扩展特性与断裂疲劳寿命研究已成为行业研究热点.关于top-down裂纹,文献[1]中考虑了老化与温度梯度对沥青路面的影响,通过对路面最大拉应力与剪应力的分析来研究其开裂机理;文献[2]中利用移动窗口技术(WMT)模拟沥青路面表面裂缝在不同工况、温度与路面结构层组合下的扩展路径.关于反射裂纹;文献[3]中采用改进的Williams级数、广义参数和等参元有限元法研究了半刚性沥青路面反射裂纹扩展特性,并使用Paris公式分析了裂纹扩展的疲劳寿命;文献[4-6]中对包含裂纹的粘弹性沥青路面的动力响应进行了研究,探讨了车辆行驶速度、阻尼比以及基层回弹模量等相关因素对裂尖应力强度因子的作用.关于路面疲劳寿命,文献[7]中为模拟反射裂纹的扩展过程,进行了路面加速试验与有限元数值模拟,预测了路面的疲劳寿命;文献[8]中研究了层间接触状态、轴载与温度对沥青面层疲劳寿命的影响.
目前大部分研究主要集中在张开型(Ⅰ型)、剪切型(Ⅱ型)等单条裂纹情形,对于移动荷载作用下的撕开型(Ⅲ型)及复合型(Ⅰ+Ⅱ+Ⅲ型)开裂研究较少,在研究中的动荷载形式多数简化为定点正弦振动荷载,沥青路面疲劳寿命评估中常考虑静态荷载下的情形,这与现实情况有所不符.
本文考虑沥青混合料的粘弹特性,以断裂力学中的应力强度因子为指标,通过ABAQUS中的子程序DLOAD与UTRACLOAD实现实车移动荷载,研究含纵横向双裂纹沥青路面在不同双裂纹间距、不同反射裂纹深度下的复合开裂力学行为;利用Paris公式计算了top-down裂纹在低速、高速、制动与静载4种荷载状态下的疲劳断裂寿命,探讨移动荷载下含纵横向双裂纹沥青路面的疲劳断裂特性.
1 模型概况
使用ABAQUS软件建立含纵横向双裂纹半刚性沥青路面有限元模型.参考文献[9],取模型长、宽、高分别为 7、6、6 m(图 1).面层上有 1条 topdown纵向裂纹,裂纹长度为3 m,基层则有1条贯穿路面横向的反射裂纹,2条裂纹的深度分别为C1、C2,反射裂纹与top-down裂纹中断面之间的间距为D.有限元模型见图2.
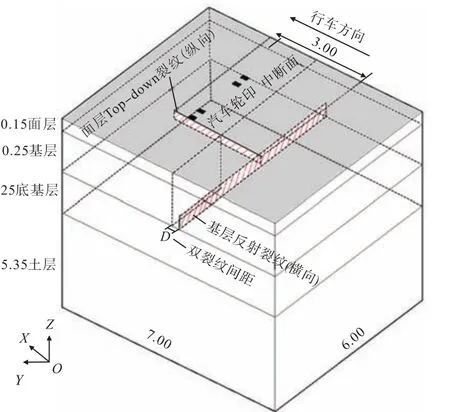
图1 模型示意(单位:m)Fig.1 Structure model(unit:m)
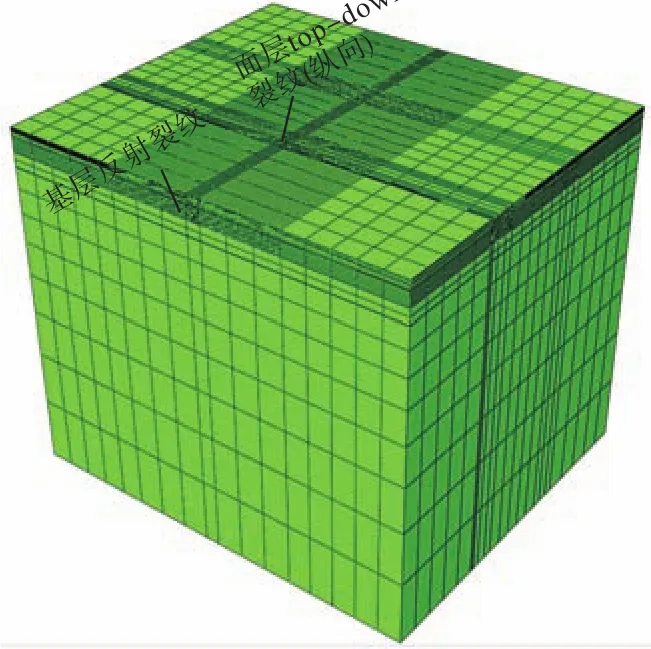
图2 有限元模型Fig.2 FEM model
考虑沥青混合料具有粘弹特性,使用广义Maxwell模型模拟沥青路面.由于ABAQUS中的广义Prony级数与该模型具有相同的数学表达形式,因此,可以较好地模拟其松弛特性.基层、底基层以及土基则使用线弹性材料来模拟,参考文献[9-10]中有关材料参数拟定本文的计算参数,各结构层参数见表1,-5℃面层粘弹性参数见表2.
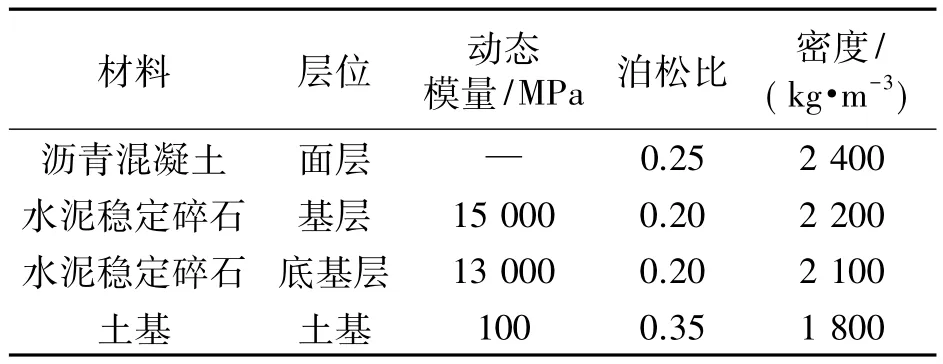
表1 路面结构各层参数Tab.1 Material parameters of different pavement layers
荷载形式为 BZZ-100,即单轴双轮荷载(图 3).垂向荷载取为 0.7 MPa[11],方向向下;为考虑水平力的作用,参考我国路面设计中计算汽车对道路水平力的方法[12],不制动情况下,取滚动摩擦因数为0.05;制动情况下,取附着系数为0.60,荷载方向与行车方向一致,水平力计算如式(1)所示.

式中:T为水平荷载;f为滚动摩擦因数或附着系数,由车辆行驶状态来确定;P为车辆的垂直荷载.

表2 面层Prony级数模型参数Tab.2 Prony parameters of the surface material

图3 BZZ-100荷载Fig.3 BZZ-100 load
使用DLOAD与UTRACLOAD分别实现垂向荷载与水平荷载的移动,其核心原理:先利用ABAQUS软件中的坐标函数控制荷载作用范围及其幅值大小;之后调用时间函数使荷载作用范围移动,轮印的移动步长由时间函数与车速相乘得到;最终通过对时间以及坐标函数的控制实现垂向、水平荷载向前移动这一加载形式.行车范围为路面中央纵向3 m区域.
计算模型基本假定:面层为粘弹性材料,基层、土基以及底基层均视为线弹性材料;路面各结构层层间位移连续;模型边界条件为四周法向约束,由于模型深度较大,故底部完全约束;整个模型处于-5℃的环境中.
2 计算结果分析
2.1 计算点位选择
采用基于应力的外推法计算应力强度因子,通常取裂纹1个截面计算,由于建立了三维模型,因此需要选择裂纹计算点位.随着荷载的移动,横向反射裂纹上各点位应力强度因子到达峰值的时程规律相同,但数值大小不同,取计算点位见图4.
top-down裂纹为纵向裂纹,裂纹方向与荷载移动方向一致,随着荷载移动,不同截面处的应力强度因子时程规律会不同.本文根据工程中的最不利原则选择计算截面.由于模型的对称性,选取top-down裂纹左半部分上的6个点,点间距离均为0.3 m,模型俯视图如图5所示.
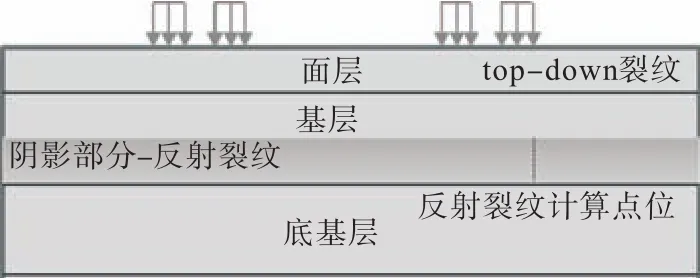
图4 反射裂纹计算点位示意Fig.4 Schem a tic of the reflective crack calculation point
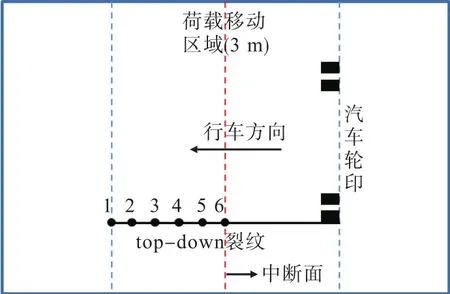
图5 top-down裂纹计算点位示意Fig.5 Schematic of the top-down crack calculation point
top-down裂纹处于垂向力与水平力共同作用下,为Ⅰ+Ⅱ+Ⅲ复合型裂纹.为综合评价Ⅰ、Ⅱ、Ⅲ型应力强度因子对裂纹扩展的影响,参考三维复合型裂纹Richard断裂准则[13],其中,Ⅰ+Ⅱ+Ⅲ复合型裂纹的等效应力强度因子为
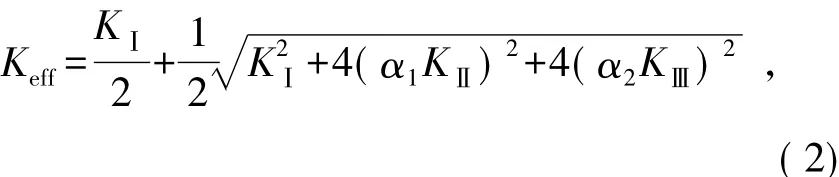
式中:KⅠ、KⅡ、KⅢ分别为Ⅰ、Ⅱ、Ⅲ型应力强度因子;Richard[13]认为,α1=1.155,α2=1.000(α1、α2为修正系数).
在计算图5中6个点位的应力强度因子时,计算模型仅考虑含1条深度为4 cm的纵向topdown裂纹,荷载以72 km/h的速度行驶,计算得出top-down裂纹上6个点位的有效应力强度因子Keff峰值,见表 3.
由表3可以看出,6号点的Keff明显比其余点位大,表明该截面是整条top-down裂纹上最容易发生裂纹扩展之处,因此,top-down裂纹的计算截面取为6号点位,即裂纹的纵向中断面.

表3 不同计算点位Keff峰值Tab.3 Keffmaxima of different calculation points
2.2 双裂纹间距对裂纹扩展的影响
该部分计算模型取top-down裂纹深度为4 cm,基层反射裂纹深度为10 cm.双裂纹间距D为基层反射裂纹平面与top-down裂纹纵向中点之间的距离,分别取为 0、100、200、300、400、500 mm,移动荷载以72 km/h(20 m/s)的速度驶过行车区域.
2.2.1 对top-down裂纹扩展的影响
不同裂纹间距下,top-down裂纹Ⅰ、Ⅱ、Ⅲ型应力强度因子的时程曲线如图6所示.
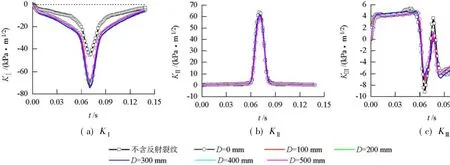
图6 不同裂纹间距下top-down裂纹Ⅰ、Ⅱ、Ⅲ型应力强度因子时程曲线Fig.6 TypeⅠ,Ⅱ,and Ⅲ stress intensity factor-time history curves of a top-down crack for different crack spacings
KⅠ为正时,对裂纹的Ⅰ型扩展起促进作用,为负时,不对裂纹扩展起促进作用;KⅡ与KⅢ不论正或负,均对裂纹扩展起促进作用[14].
由图6(a)可知,整个时间段内的KⅠ均为负值,在移动荷载作用下top-down裂纹发生Ⅰ型裂纹扩展的可能性较小.由图6(b)可知,随着荷载的移动,KⅡ逐渐增大,在中点处达到峰值,之后慢慢减少到0,且Ⅱ型剪切方向始终不变.由图6(c)可知,KⅢ先从正值逐渐降低至负峰值,再突然增加到正值,然后再减小至负值,最后逐渐趋于平缓,故Ⅲ型剪切方向处于前后交替变化.
不同双裂纹间距下的KⅡ差别很小,单条裂纹时KⅡ峰值最大,D=0时KⅡ峰值最小,分别对应Ⅱ型裂纹扩展最严重以及最轻微的情况,随着裂纹间距的增大,KⅡ峰值并没有发生明显的变化.单条裂纹情形下的Ⅲ型裂纹扩展同样最为严重,随着裂纹间距的逐渐增大,KⅢ峰值也没有发生明显变化,因此,双裂纹间距对top-down裂纹扩展影响甚微.同时,KⅢ小于KⅡ1个数量级,因此,top-down裂纹的扩展以Ⅱ型为主.
利用Richard[13]准则计算有效应力强度因子,考察不同双裂纹间距下top-down裂纹的综合扩展情况(图7).由图7可知,在单条裂纹情形下,裂纹最容易发生扩展;在D=0时,裂纹则处于最不易扩展状态,且间距大小不会对Keff峰值产生较大的影响;Keff时程规律与KⅡ一致,进一步说明Ⅱ型扩展在top-down裂纹扩展过程中起主导作用.
综上所述可以看出,由于基层的反射裂纹分担了作用在top-down裂纹上的荷载,降低了面层裂纹有效应力强度因子,因此,存在反射裂纹将减缓top-down裂纹扩展.
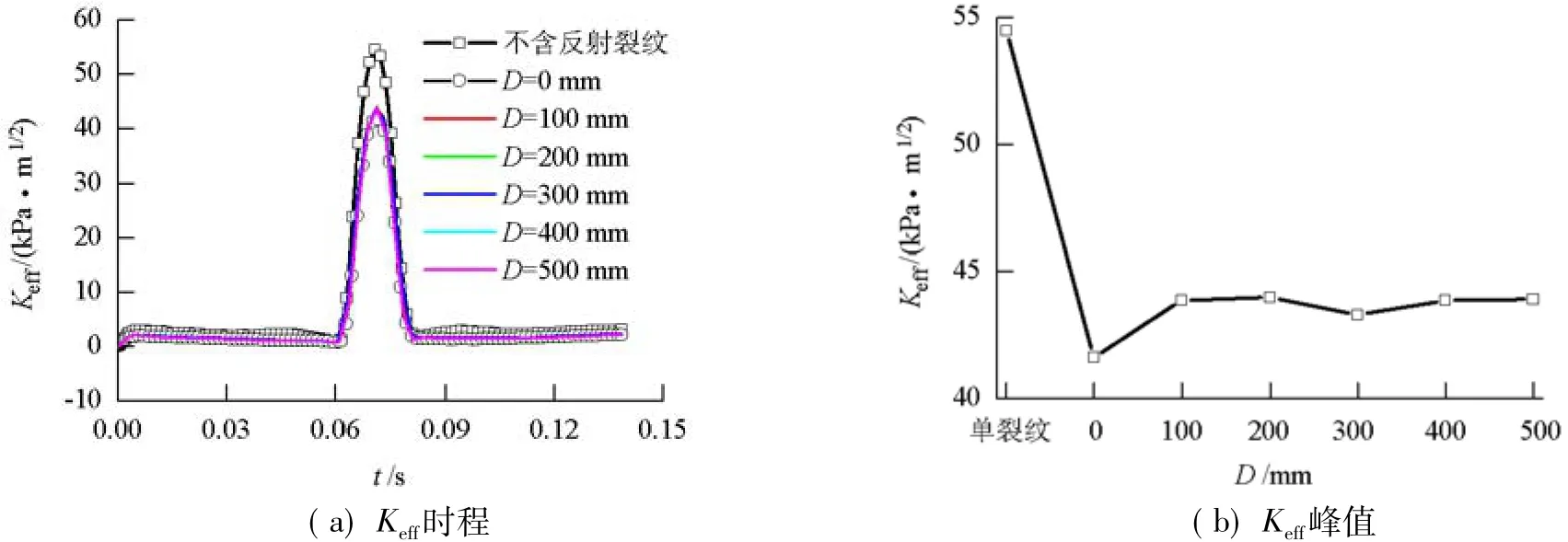
图7 不同裂纹间距下Keff变化规律Fig.7 Keffvariation diagram for different crack spacings
2.2.2 对反射裂纹扩展的影响
基层底部的反射裂纹为横向裂纹,随着荷载的移动,并不会产生横向剪切作用,因此为Ⅰ+Ⅱ型复合式裂纹.采用文献[15]中Pook准则计算Ⅰ+Ⅱ型复合型裂纹有效应力强度因子,如式3所示.
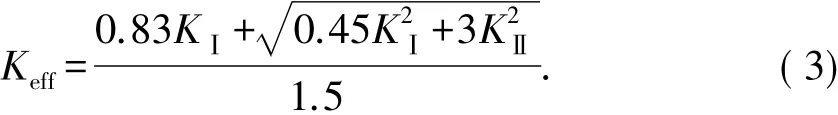
图8为不同裂纹间距下反射裂纹应力强度因子时程曲线.
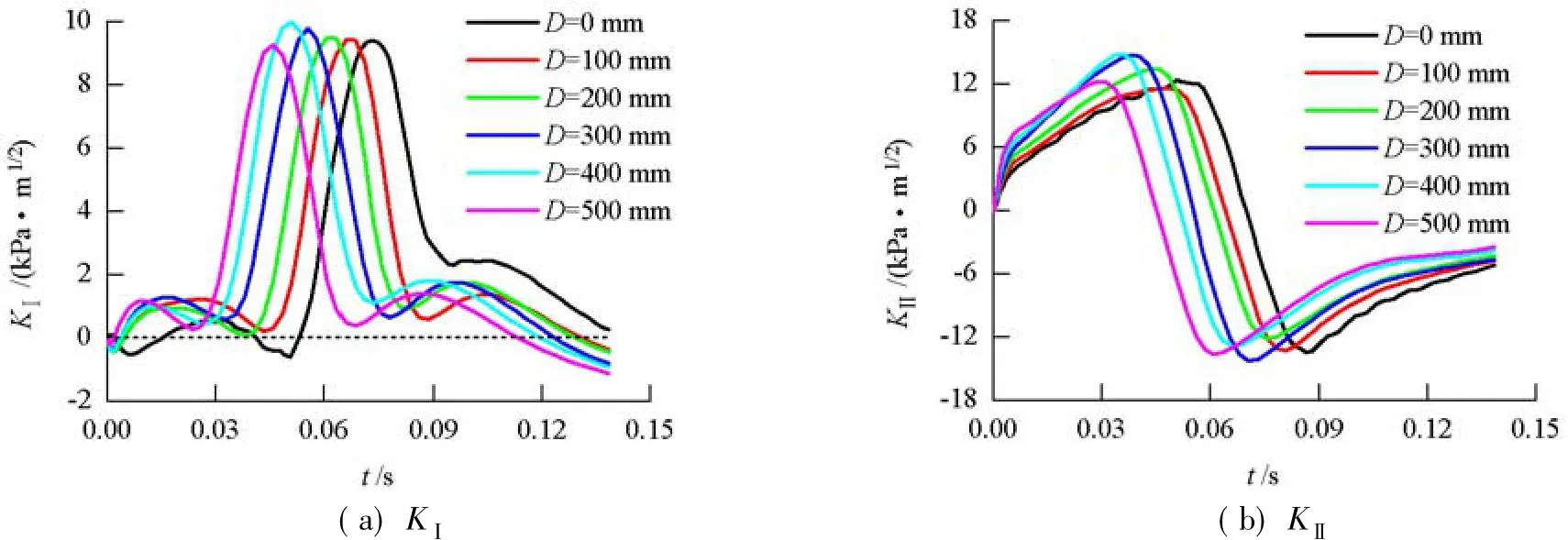
图8 不同裂纹间距下反射裂纹应力强度因子时程曲线Fig.8 Stress intensity-time history curve of a reflective crack for different crack spacings
由图8(a)可知,KⅠ整体呈现先增大后减小的趋势,当荷载作用在反射裂纹正上方时,KⅠ达到峰值;由于KⅠ总体上为正值,故荷载对反射裂纹的Ⅰ型扩展起促进作用.由图8(b)可知,KⅡ先逐渐增大到正峰值,再迅速降低到负峰值,之后逐渐趋于平缓,反射裂纹的Ⅱ型剪切方向产生交替变化.与KⅠ不同,当荷载作用于反射裂纹正上方时,KⅡ=0.KⅠ与KⅡ值相差不大,因此,反射裂纹的Ⅰ、Ⅱ型裂纹扩展程度相当.
表4为不同裂纹间距下反射裂纹Keff峰值.

表4 不同裂纹间距下反射裂纹Keff峰值Tab.4 Keffmaxima for different crack spacings
结合图8与表4可知,不同双裂纹间距下,反 射裂纹Ⅰ、Ⅱ型应力强度因子峰值差别不大,当D=400 mm时,KⅠ、KⅡ及 Keff峰值均为最大值,故反射裂纹最易发生Ⅰ型与Ⅱ型裂纹扩展,裂纹综合扩展程度也最大.
2.3 反射裂纹深度对裂纹扩展的影响
取 C1=4 cm,C2=4,6,8,10,12 cm,D=0,荷载移动速度为72 km/h.
2.3.1 对 top-down 裂纹扩展
不同反射裂纹深度对应的top-down裂纹应力强度因子时程曲线如图9所示.由图9可知,不同反射裂纹深度下top-down裂纹Ⅰ、Ⅱ、Ⅲ型应力强度因子相差很小.由于KⅢ全过程均为负值,因此,top-down裂纹发生Ⅰ型裂纹扩展的可能性较小.Ⅰ、Ⅱ、Ⅲ型应力强度因子不随着C2的增大而单调变化,其峰值之间的差别很小.由图10可知,topdown裂纹大致在时程中点处裂纹扩展最为严重;Keff峰值之间的差距也较小,当C2=4 cm时,topdown裂纹最易发生开裂扩展,当C2=8 cm时,开裂扩展综合程度相对最低.
2.3.2 对反射裂纹扩展
图11为反射裂纹在不同深度下KⅠ与KⅡ时程曲线.

图9 不同C2下top-down裂纹Ⅰ、Ⅱ、Ⅲ型应力强度因子时程曲线Fig.9 TypeⅠ,Ⅱ,and Ⅲ stress intensity factor-time history curves of a top-down crack under different C2
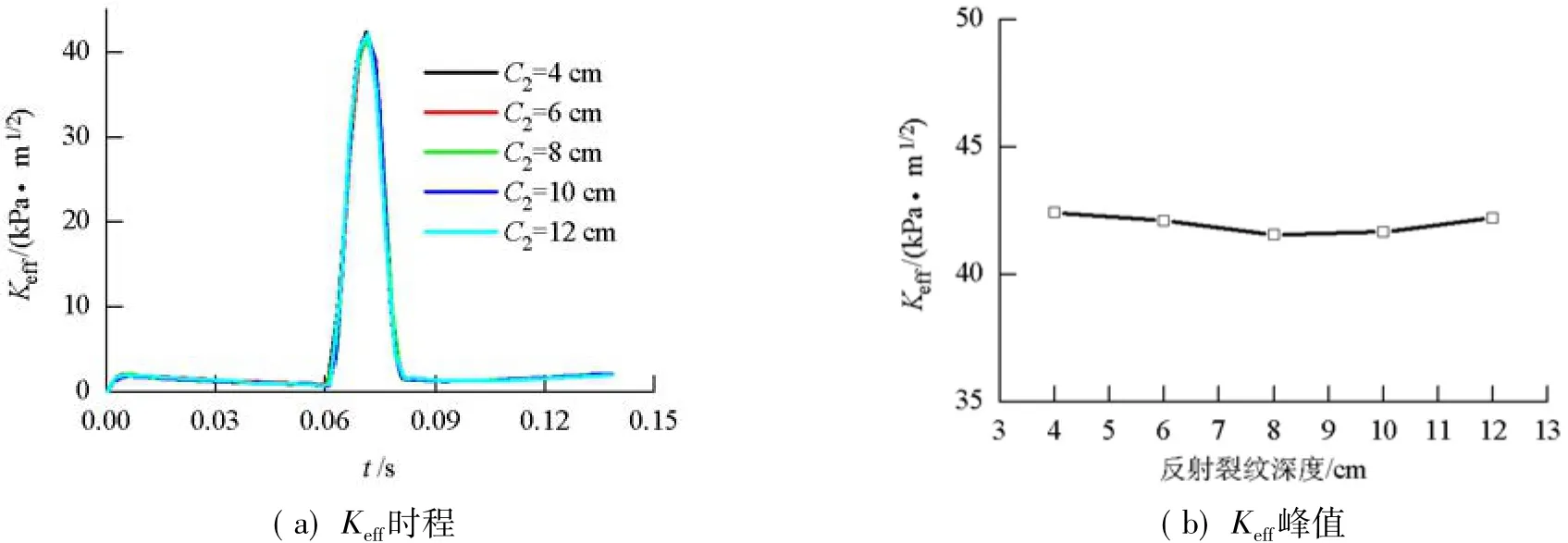
图10 不同反射裂纹深度下Keff变化规律Fig.10 Keff variation diagram for different reflection crack depths
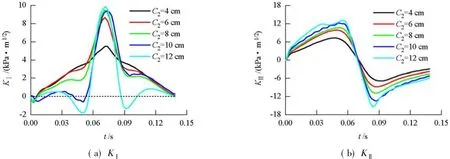
图11 不同反射裂纹深度下反射裂纹应力强度因子时程曲线Fig.11 Stress intensity factor-time history curves of a reflective crack for different crack depths
由图11可以看出:随着C2的增大,Ⅰ、Ⅱ型应力强度因子幅值均有增加;KⅠ峰值两侧值的规律与峰值相反,随着反射裂纹深度的增大而减小.
表5为不同C2下反射裂纹Keff峰值.由表5可知,随着反射裂纹深度的增加,反射裂纹Ⅰ、Ⅱ型扩展程度逐渐加大,且综合扩展程度也越来越大.

表5 不同C2下反射裂纹Keff峰值Tab.5 Keffmaxima of a reflective crack under different C2
3 疲劳断裂寿命预估
本文中采用经典的Paris公式来计算topdown裂纹的疲劳断裂寿命.鉴于在移动荷载的竖向力与水平力综合作用下的top-down裂纹为Ⅰ+Ⅱ+Ⅲ型复合式裂纹,使用Richard准则[13]计算有效应力强度因子的最大幅值Keff-max,如式(4)所示.
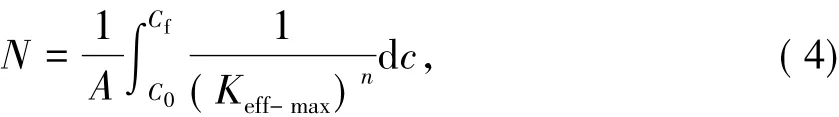
式中:c为裂纹深度;C0、Cf分别为裂纹初始深度和疲劳破坏时的深度;N为荷载循环次数,即疲劳寿命;A、n为材料疲劳常数.
[4]对 A与 n的取值(n=4.5,A=10-7.49),本文中取面层 C0=1 cm,计算 top-down裂纹在动、静态荷载下从初始深度扩展到面层厚度2/3这一过程的疲劳寿命N.
模型中取反射裂纹深度为10 cm,D=0 mm.在低速(36 km/h)、高速(108 km/h)及静态荷载下,水平力系数为0.05;在以-5 m/s2加速度制动时(初速度为72 km/h),水平力系数为0.6.为使用式(4)计算top-down裂纹的疲劳寿命,分别计算了top-down裂纹在不同深度情形下的Keff-max,将不同深度下top-down裂纹的Keff-max进行多项式拟合,再代入式(5),即可进行数值积分计算得到疲劳寿命.
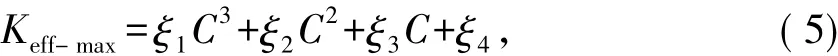
式中:ξ1、ξ2、ξ3、ξ4为多项式拟合系数;C 为 topdown裂纹深度.
经计算后,4种荷载状态下top-down裂纹有效应力强度因子幅值拟合的多项式如表6所示,表中,R2为拟合度.

表6 不同荷载状态下Keff-max拟合多项式Tab.6 Keff-maxfitting polynomials for different loads
将表6中的多项式代入式(4)进行计算,得到4种荷载状况下top-down裂纹的疲劳断裂寿命(表7).由表7可知,高速行驶状态下的疲劳断裂寿命大于低速及静态荷载下的疲劳寿命,低速行驶时,top-down裂纹更容易发生疲劳扩展;当车辆制动时,由于水平力较大,使得top-down裂纹的疲劳寿命大大减小,断裂疲劳寿命仅为高速情形下的20.4%.

表7 不同荷载状态下top-down裂纹疲劳寿命Tab.7 Top-down crack fatigue life under different loading conditions
4 结论
(1)在移动荷载作用下,整条top-down纵向裂纹发生综合裂纹扩展最严重处在裂纹的中断面.
(2)top-down纵向裂纹在移动荷载下以Ⅱ型开裂扩展为主,双裂纹间距对其Ⅱ、Ⅲ型扩展影响不大;在单裂纹情形下的裂纹扩展最为严重,双裂纹间距为0时裂纹扩展最轻微;存在基层反射裂纹可以减缓top-down裂纹的扩展;不同双裂纹间距下的反射裂纹更容易发生Ⅰ、Ⅱ型裂纹扩展,当双裂纹间距为400 mm时,反射裂纹最容易发生扩展.
(3)反射裂纹深度为4、8 cm时,分别对应top-down裂纹综合扩展程度最严重以及最轻微两种极端情形,随着反射裂纹深度增大,反射裂纹Ⅰ、Ⅱ型开裂扩展程度逐渐增大,但总体表现反射裂纹深度对top-down裂纹开裂扩展的影响较小.
(4)不同荷载状态下top-down裂纹的断裂疲劳寿命不同.高速行驶状态下的疲劳断裂寿命最长,制动行驶状态下的最短;制动荷载将大大缩短top-down裂纹的疲劳断裂寿命,因此在汽车制动路段应加强沥青路面的抗裂设计.
参考文献:
[1] 张永平,陆永林,张洪亮,等.基于弹性理论的沥青路面top-down开裂机理研究[J].公路交通科技,2014,31(4):16-21.ZHANG Yongping,LU Yonglin,ZHANG Hongliang,et al.Study on top-down cracking mechanism in asphalt pavement based on theory of elasticity[J].Journal of Highway and Transportation Research and Development,2014,31(4):16-21.
[2] 毛成,邱延峻,李云鹏.沥青路面表面裂纹扩展模拟及影响因素分析[J].西南交通大学学报,2004,39(4):437-441.MAO Cheng,QIU Yanjun,LI Yunpeng.Simulation of surface crack propagation in asphalt pavements and analysis ofits influential factors[J]. Journal of Southwest Jiaotong University,2004,39(4):437-441.
[3] 徐华.半刚性基层沥青混凝土路面反射裂缝扩展和疲劳寿命研究[D].南宁:广西大学,2012.
[4] 苗雨,万云冬,张邵敏.含反射裂纹沥青路面的动力响应分析[J].岩土力学,2009,30(8):2511-2516.MIAO Yu,WAN Yundong,ZHANG Shaomin.Dynamic response analysis of asphalt pavement with reflective crack[J].Rock and Soil Mechanics,2009,30(8):2511-2516.
[5] 黄志义,王金昌,朱向荣.动荷载下含反射裂缝沥青路面结构黏弹性分析[J].浙江大学学报:工学版,2007,41(1):114-119.HUANG Zhiyi, WANG Jinchang, ZHU Xiangrong.Viscoelastic analysis of asphalt pavement with reflective cracks and subjected to dynamic loading[J].Journal of Zhejiang University: Engineering Science, 2007,41(1):114-119.
[6] 梁俊龙,高江平,苌亮.基于动态模量的含多裂缝沥青路面开裂分析[J].广西大学学报:自然科学版,2016,41(1):246-252.LIANG Junlong, GAO Jiangping, CHANG Liang.Cracking analysis of asphalt pavement with multi-crack based on dynamic modulus[J].Journal of Guangxi University:Nat.Sci.Ed.,2016,41(1):246-252.
[7] PEREZ S A,BALAY J M,TAMAGNy P,et al.Accelerated pavement testing and modeling of reflective cracking in pavements[J]. Engineering Failure Analysis,2007,14(8):1526-1537.
[8] 黄兵,艾长发,阳恩慧,等.考虑层间状态的沥青面层动应变疲劳数值分析[J].西南交通大学学报,2014,49(4):682-686.HUANG Bin, AIChangfa, YANG Enhui, etal.Numericalanalysisofdynamic strain and fatigue characteristics of asphalt layer considering interlayer condition[J].Journal of Southwest Jiaotong University,2014,49(4):682-686.
[9] 肖川.典型沥青路面动力行为及其结构组合优化研究[D].成都:西南交通大学,2014.
[10] 彭彬.沥青路面低温开裂数值模拟与参数分析[D].南京:东南大学,2009.
[11] 中交公路规划设计院.JTG D50—2006公路沥青路面设计规范[S].北京:人民交通出版社,2006.
[12] 孙家驷,高建平.道路设计资料集4[M].北京:人民交通出版社,2003:63-64.
[13] RICHARD H.A,FULLAND M,BUCHHOLZ F G,et al.3D fracture criteria for structures with cracks[J].Steel Research,2003,74(8):491-497.
[14] 赵延庆,王抒红,周长红,等.沥青路面top-down裂缝的断裂力学分析[J].同济大学学报:自然科学版,2010,38(2):218-222.ZHAO Yanqing,WANG Shuhong,ZHOU Changhong,et al.Analysis of top- down cracking of asphalt pavements based on fracture mechanics approach[J].Journal of Tongji University:Natural Science,2010,38(2):218-222.
[15] 朱莉.三维复合型脆性断裂行为的数值计算与实验研究[D].哈尔滨:哈尔滨工程大学,2012.

