水库蓄水对山区桥址风特性的影响

王云飞， 汪 斌， 李永乐

(西南交通大学土木工程学院，四川成都610031)

抗风设计是山区大跨度桥梁重要的设计内容之一，进行大跨度桥梁抗风研究之前最首要的就是准确地获取桥址区的风特性参数［1］.一般的跨海、跨江大桥以及常规地形下的桥址区风特性具有相对均一性，复杂山区风特性有着复杂的空间分布，而且缺乏历史气象资料记录，也没有切实的规范可供参考［2-3］.随着我国西部大开发战略的深入发展，西部山区交通设施建设得到进一步加强，受线路以及山区地形特征的要求，较多的山区大跨度桥梁得到修建.因此，开展复杂山区地形条件下的桥址区风特性研究对山区大跨度桥梁建设极其重要.

西部山区河流落差大，是我国水电站的有利建设地点.随着大型水电站的修建，坝址上游水位明显抬高，上游水体面积增大，这将导致原来低于库区水位的坝体上游峡谷沟壑地貌被水淹没，使得库区的地形地貌在大坝蓄水之后发生巨大变化［4］.水库蓄水所形成的水面不但会改变库区峡谷的原始地貌，同时也会导致峡谷内风场特性的改变.在实际工程中，受线路要求，有相当数量的桥梁工程必须要跨越或邻近水库库区.当大跨度桥梁跨越大坝库区的时候，大坝蓄水后会对原桥址区风特性造成一定的影响.这使得依照原有山区地形条件风特性进行抗风设计的大跨度桥梁在水库蓄水后承受未知的新风环境，有可能会对桥梁抗风造成未知的影响.现在国内外文献中并没有关于山区大坝对库区桥位风场影响的研究报道.

获取山区风环境特性的方法一般有3种，现场实测、风洞试验和 CFD(computationalfluid dynamics)数值模拟技术.其中CFD数值模拟具有诸多优点，如成本低、易重复性、不受试验条件约束等，因而受到广大学者的重视［5-9］.Xiao 等［10］采用多种湍流模型，对6.9 km×10.1 km 范围的地形进行了模拟研究，最后与现场实测的结果进行了验证.邓院昌等［11］采用数值模拟的方法研究了地表粗糙度对实际地形风场的影响.Abdi和Bitsuamlak［12］采用数值模拟技术对不同地形条件采用不同的湍流模型进行了研究.周志勇等［13］为研究网格类型和网格尺度划分对计算结果的影响，进行了27 km×23 km的大范围区域复杂地形的风环境CFD模拟.李永乐等［14］对边长为8 km的方形区域进行CFD模拟，研究了西部复杂山区风场的空间分布特性，为山区桥梁抗风提供了一些建议.因此本文研究水坝蓄水后桥位风场的变化具有一定探索性.

本文以西部山区某大跨度悬索桥桥址区为工程背景，在桥位下游1.9 km处将要修建一座水电站，水库正常蓄水位为 2 010 m(距离桥面50 m)，谷底高程为1 801 m，水位变化高达209 m，如图1所示.另外该桥址区地表起伏剧烈，两岸山峰海拔高度分别接近5 400 m和5 600 m，山峰至河谷底的最大海拔相差超过3 800 m，属于典型的山区深切峡谷地形.本文采用CFD数值模拟方法，分别建立了原始地形和坝前水库蓄水后的地形数值模型，分析了两种模型下的风场特性，探讨了桥址区风速的分布特点，明确了水库蓄水对桥址区风场分布的影响规律.

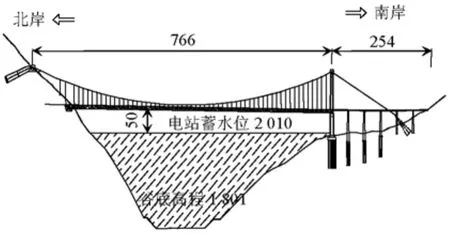
图1 桥位高程(单位:m)Fig.1 Overall configuration of the bridge in case study(unit:m)

1 实体建模及网格划分

针对桥址区地形地貌的复杂性，所选定的计算区域应足够大，以使流场得以充分发展.结合当前计算资源，以桥位为中心选定大小为 20 km×20 km的区域作为分析对象.建立地形几何模型时，首先在获取桥位的CAD地形图后，通过CAD中的lsp文件编程获取区域地形图上的高程数据点坐标，接着将得到的地形高程数据经Matlab插值处理形成标准的格点数据.在CFD建模软件Gambit中基于NURBS(非均匀有理B样条)的曲面建模方法，将高程格点数据拟合为地形几何曲面.此方法能保证拟合的曲面经过各个高程点后变得较光滑，且精度较高.在建立水库蓄水后的地形曲面时，首先将大坝上游所有被淹没区域数据点的高程修正到蓄水后水面高程处，最后重新使用Gambit来拟合得到大坝蓄水后的地形表面，如图2所示.

图2 大坝蓄水后的地形表面Fig.2 Geometric terrain after water storage

计算区域底部以山体、河流为界，最低高程为1 660 m，顶部高程为11 260 m.采用专业流体网格划分软件ICEM对建立的地形表面之上的计算区域进行网格划分，网格的离散采用适应性更强的四面体网格，地表网格分辨率达到60 m.在分析之前，为进行网格无关性分析，以60°来流风向下的原始模型为例进行了3种网格尺度的分析.

(1)290万网格:地形底面网格分辨率为100 m.边界层划分为3层，总高度为42 m，第1层网格高10 m.

(2)380万网格:地形底面网格分辨率为100 m.边界层8层，第1层5 m，总高为80 m.

(3)424万网格:地形底面网格分辨率为60 m.边界层划分为4层，总高度为35 m，第1层网格高5 m.

主梁各测点计算结果如图3所示.可知这几种网格尺寸计算得到的结果整体趋势相同，相差较小.考虑424万网格精度更高，同时考虑计算机资源基本满足要求，最终选定424万网格模型.两个模型采用相同的参数进行网格划分，无水坝模型网格总数424万，有水坝模型网格总数422万，近地层棱柱体网格局部示意如图4所示.

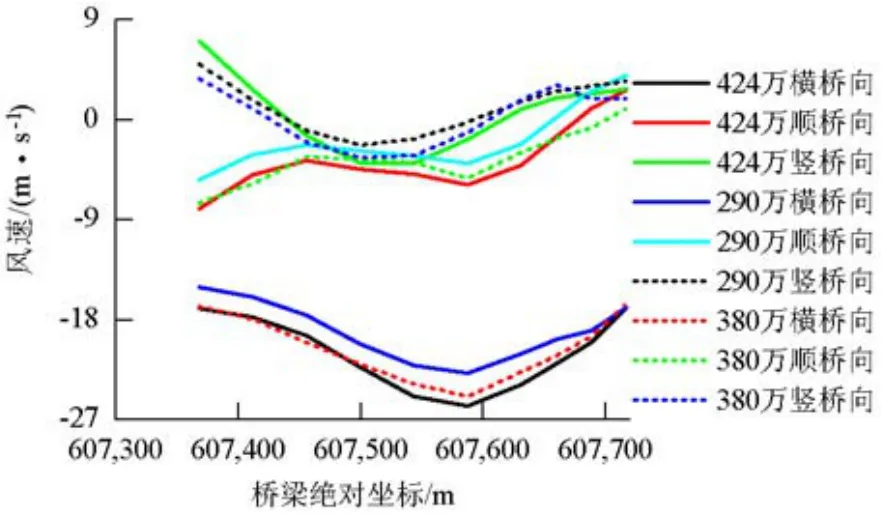
图3 原地形不同网格尺度下风速计算结果(60°)Fig.3 Wind velocity under different meshing scales oft he origin terrain(60°)

图4 边界层网格局部示意Fig.4 Local sketch of boundary layer mesh

2 求解参数及边界条件设置

桥位地形风场数值模拟可简化为不可压缩流体.采用有限体积法(finite volumn method，FVM)对不可压缩流动控制方程进行离散，基于商用软件Fluent进行计算分析，选用全隐式分离求解器和SST k-ω湍流模型.速度与压力的耦合为IMPLEC算法，湍动耗散率、湍动能、动量、压力的离散都采用的是二阶迎风格式［15］.

文献［14］中来流风速的设置方法，采用B类地表(气象站标准场地)对应的风速廓面作为入口来流风速分布.梯度风速vT=50 m/s.考虑到桥位属于高海拔深切峡谷地带，梯度风高程可取3 600 m，而低于高程3 600 m的部分按指数规律进行设置(B类地表指数律).所选区域地形最低点高程为1 660 m，则易知该区域梯度风高度为1 940 m.来流风速vH可用式(1)表示，桥面高度入口处风速为 38.91 m/s.

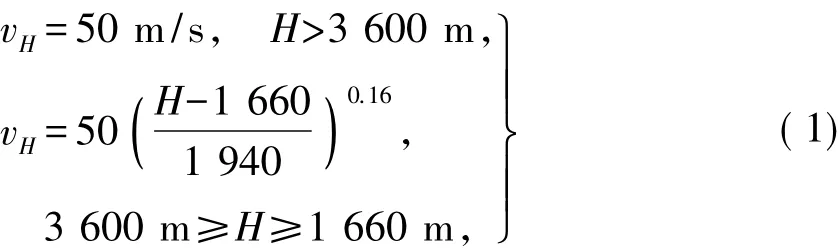
式中:H为高程.

截至2017年底，我国地源热泵装机容量达2万兆瓦，位居世界第一，年利用浅层地热能折合1900万吨标准煤，实现供暖（制冷）建筑面积超过5亿平方米，主要分布在北京、天津、河北、辽宁、山东、湖北、江苏、上海等省市的城区。我国地热能直接利用以供暖为主，其次为康养、种养殖等。近10年来，我国水热型地热能直接利用以年均10％的速度增长。

3 计算结果及分析

3.1 工况设置

在模拟之前，首先沿桥面高度主梁轴向方向布置10个风速监测点.监测点的位置分布从右至左分别为1/4边跨、1/2边跨、3/4边跨、索塔、1/8主跨、1/4主跨、3/8主跨、1/2主跨、5/8主跨、3/4主跨，如图5所示.为考察桥位风速沿高度的变化特性，分别在桥塔位置处和主跨跨中位置沿高度方向布置若干监测点.沿高度方向风速梯度总体上变小，由此监测点间距布置由下到上逐渐增大(图5).为全面考察不同来流风向下桥位风场的分布规律，按顺时针从正北方向每隔10°作为一个来流工况，总计36个计算工况，如图6所示.

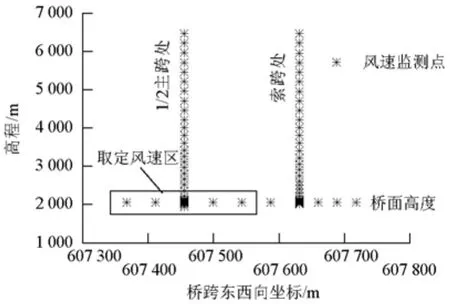
图5 风速监测点分布Fig.5 Distribution of wind velocity observation points

图6 来流风向示意Fig.6 Sketch of wind directions involved

分别用u、v、w表示横桥向风速、顺桥向风速、竖向风速分量，计算结果中的风向角α和风攻角β定义分别如式(2)、(3).其中:正攻角表示气流的上升，负攻角表示气流的下降;风向角是按照来流从河谷北岸吹向河谷南岸为正，相反就为负.

3.2 蓄水对主梁跨向风特性的影响

为分析各来流工况下水库蓄水对主梁跨向风特性的影响，以跨向各测点的横桥向风速增量平均值来度量蓄水前后各工况下风速值的变化，以风速相关系数(蓄水前后跨向各测点横桥向风速的标准协方差)来分析蓄水前后各工况下风速分布规律的变化，结果如图7所示.

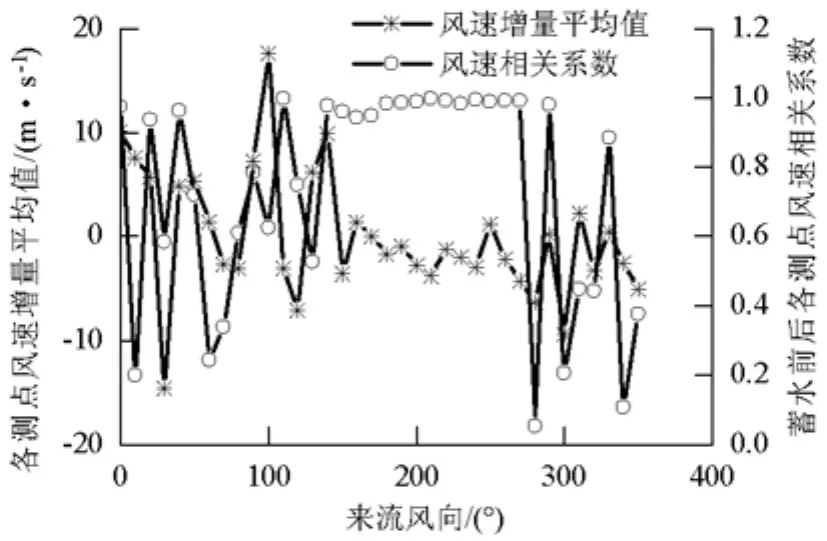
图7 蓄水对主梁跨向风特性的影响Fig.7 Influence of water storage on wind characteristic along bridge deck

由图7可知:

(1)各测点风速增量均值在大多数来流工况下变化较大，这表明沿主梁跨向的各测点风速分布在多数工况下对蓄水的影响比较敏感，大坝蓄水后主梁风速分布与无蓄水时有不同程度的较大变化.这是由于蓄水导致上游大面积区域地形形状发生巨大改变，而且桥梁主梁比较靠近蓄水位(距离蓄水位50 m)，因此沿跨向各测点的风速对地形变化更为敏感，典型来流工况下(90°)的主梁风速分布如图8所示.

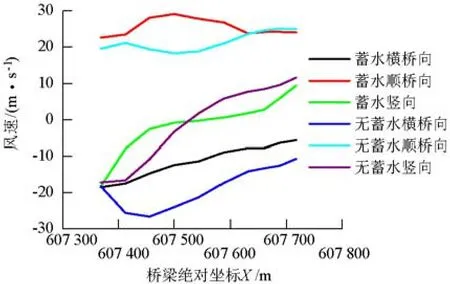
图8 主梁风速分布(90°)Fig.8 Wind velocity distribution along bridge deck(90°)

(2)跟其他工况相比，当来流方向位于200°～260°时，蓄水前后各测点风速相关系数接近于1，表明蓄水前后各测点风速几乎线性相关，即各测点分布规律非常相似.同时可以发现，这几个工况下各测点风速增量平均值也较其他工况变化小得多，即蓄水前后风速值变化较小.分析认为在200°～260°来流工况下，来流风向位于桥位河道走向与上游主流河道走向附近，使得风沿上游较宽阔的河道流动，气流所受阻挡较小.并且来流风是从坝址上游吹向下游，避开了反向来流时大坝位置处地形突变的阻挡.所以与其他来流工况相比，水坝蓄水对主梁风速分布规律影响相对较小，典型来流工况下(200°～260°)沿主梁跨向从河谷北岸到南岸各测点横桥向风速呈现递减的规律，220°来流下的分布如图9所示.

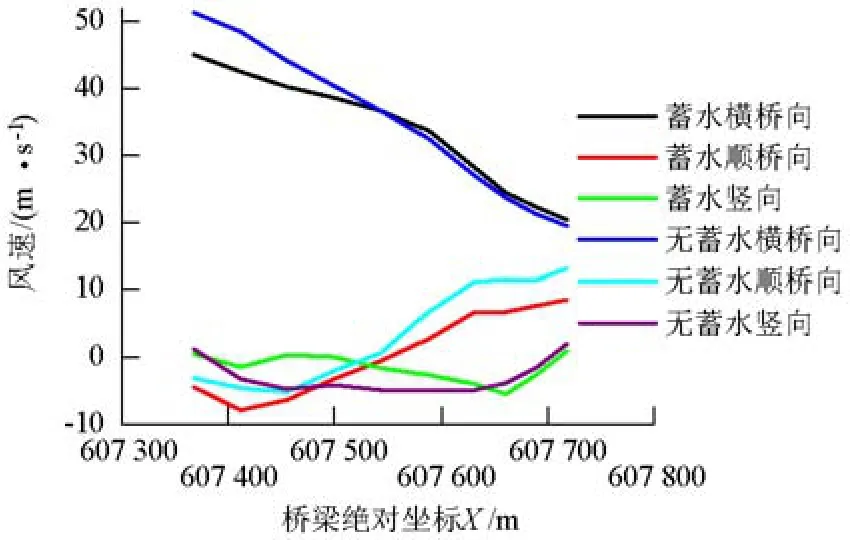
图9 主梁风速分布(220°)Fig.9 Wind velocity distribution along bridge deck(220°)

3.3 蓄水对主梁横桥向平均风速的影响

取定图5风速区中跨中位置附近的5个监测点作为代表，将这5个点的横桥向风速平均值作为主梁不同工况下的横桥向平均风速，以反映对主梁影响比较大位置的横桥向风速.有无蓄水情况下主梁横桥向平均风速的绝对值在不同工况的分布如图10所示.由图10可知:有无蓄水情况下主梁横桥向平均风速在不同工况下变化复杂，但二者在各来流工况下的整体分布规律基本一致;与无蓄水结果相比，除个别工况外，大坝蓄水后主梁横桥向平均风速在各来流工况下均有不同程度的降低.原因可能来自于两方面:一方面水库淹没的那部分峡谷对空气的压缩效应消失，另一方面水面抬高了零风速平面.有无蓄水情况下主梁横桥向平均风速均在来流风向角为200°～260°范围内达到最大.表1给出了这几个工况下的风速放大系数(放大系数取为主梁横桥向平均风速与桥面高度处入口风速的比值).由表1可知:无蓄水时，在220°和230°来流工况下的最大风速放大系数分别达到1.14和1.13，有明显的峡谷风效应;当大坝蓄水后，在220°和250°来流工况下，最大风速放大系数为 1.05和1.06，峡谷风效应明显减小.

表1 工况风速放大系数(200°～260°)Tab.1 Wind velocity amplification coefficient(200°～260°)

3.4 蓄水对主梁平均风向角及风攻角的影响

选择与3.3节相同的5个监测点，将其风向角或风攻角结果取平均值，以此来确定在各工况下主梁平均风向角及风攻角的分布特点.图11、12分别为有无蓄水下的主梁平均风向角、主梁平均风攻角随来流的变化情况.

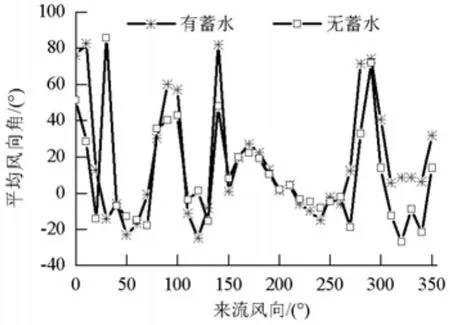
图11 各工况下主梁平均风向角Fig.11 Averaged wind direction

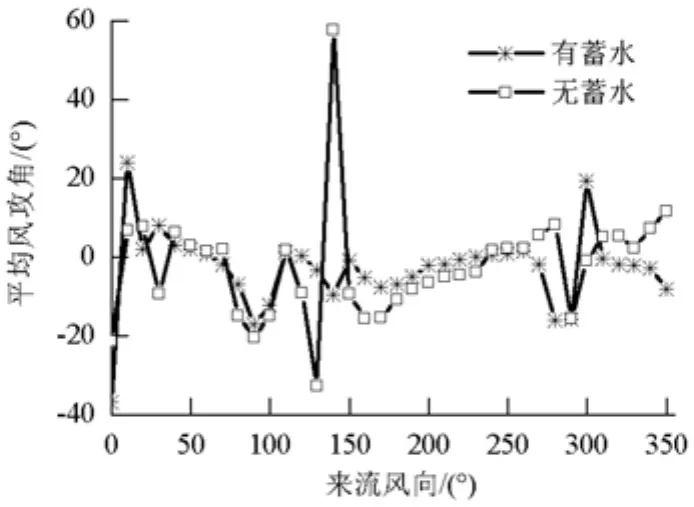
图12 各工况下主梁平均风攻角Fig.12 Averaged wind attack angle

图13、14分别为有无蓄水情况下主梁横桥向平均风速绝对值和风攻角的联合分布图.由图13、14可知:主梁在有无蓄水两种情况下均出现较大的负攻角效应;无蓄水时出现较明显的大正攻角，蓄水时主梁正攻角效应明显减弱，可能是由于水坝蓄水后在桥位下方形成的水平面覆盖了峡谷内原始复杂地貌，使得低空风流动过程中受到的干扰减弱，竖向风速分量减小所致.图13、14中实线为各工况的包络线，可以确定横桥向风速与风攻角的对应情况.同时可以发现，对处于包络线外的其他大风攻角，由于其对应的横桥向平均风速较小，并不能对结构的抗风性能起控制作用.风速与风攻角包络值如表2所示，由表2可知，蓄水时主梁各攻角对应的横向平均风速均有较明显的降低.

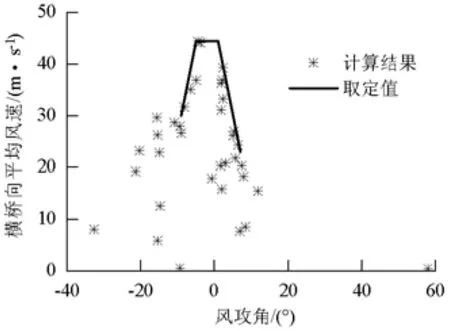
图13 蓄水时平均风速随攻角的变化Fig.13 Variation of averaged wind velocity with wind attack angle without water storage

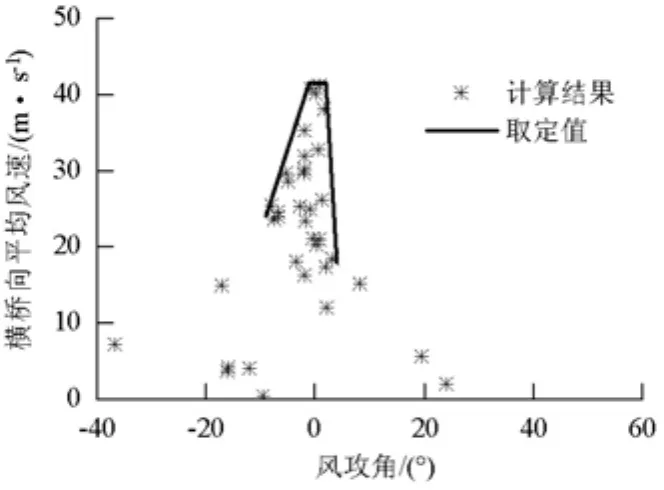
图14 无蓄水时平均风速随攻角的变化Fig.14 Variation of averaged wind velocity with wind attack anglewith water storage

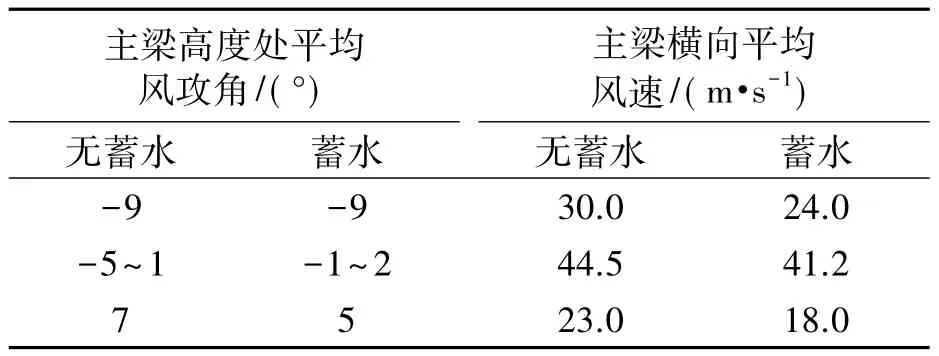
表2 风速与风攻角包络值Tab.2 Envelop value of wind velocity and attack angles

3.5 风特性沿高度的分布

以250°来流工况下主跨跨中和索塔处风速结果为例来说明风特性沿高度的分布规律.图15、16分别为250°来流工况下主跨跨中和索塔处风速竖向剖面图.当高程很高时(如5 500 m左右)，风速随高度增加不再变化，地表情况不再产生影响，气流也得以充分发展，表明设置的计算域的高度是合理的，边界顶部没有对计算域流场造成干扰.由于桥位处地貌的复杂多变性，风速剖面的变化规律远不同于常规地形条件下的指数律或对数律.由于桥址区巨大的地形海拔落差，同时由于大坝蓄水造成的对区域地形的巨大变化，各工况下风速的竖向分布规律在较大的高程范围内均产生了变化.由图15、16可知，在 200°～260°典型工况范围内有无蓄水条形的风速剖面整体规律相似，但在较低海拔(约3 000～3 500 m)范围内时风速剖面差别较大，随着海拔高度的继续增加，风速分布逐渐趋于相同.

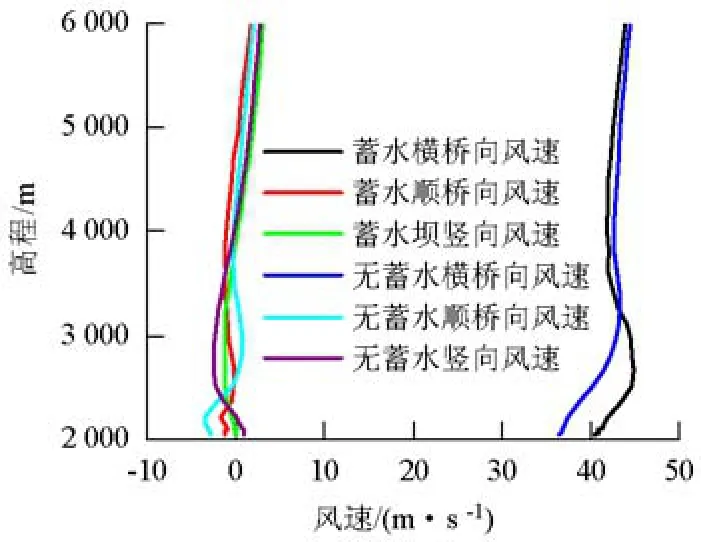
图15 主跨跨中竖向风剖面Fig.15 V ertical wind profile in the mid-span

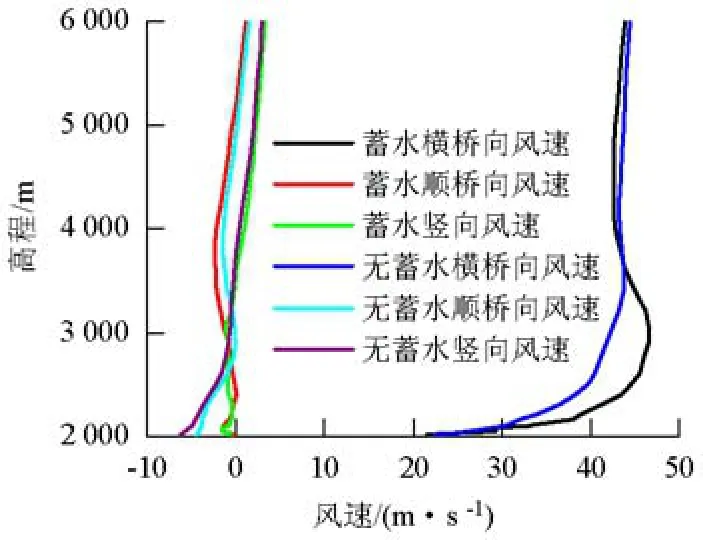
图16 索塔处竖向风剖面Fig.16 Vertical wind profile at bridge tower

4 结 论

通过对比山区有无水库蓄水两种情况下桥址区风特性，可得出如下结论:

(1)当来流方向位于200°～260°范围内时，两个模型主梁跨向各测点风速分布规律相近，远比其他工况下的差异要小.由于桥梁北岸山脊作用，这几个工况下主梁跨向各测点的横桥向风速从河谷北岸向南岸均呈现出递减规律.

(2)两个模型的主梁横桥向平均风速在各工况下的整体变化规律基本一致.与无水坝结果相比，除个别工况外，大坝蓄水后主梁横桥向平均风速在各来流工况下均有不同程度的降低.

(3)两个模型的主梁横桥向平均风速均在来流工况为200°～260°内时达到最大.无水坝时风速放大系数最大值为1.14，有明显的峡谷风效应;大坝蓄水后，最大风速放大系数为1.06，峡谷风效应明显减小.

(4)除个别工况外，两个模型主梁平均风向角及风攻角随来流风向的变化规律比较相近.两种情况下主梁均有较大负攻角效应，无水坝时还有较明显的大正攻角效应，而有水坝时主梁正攻角效应明显减弱.

(5)两种模型风速剖面整体规律相似，但在低海拔(约3 000～3 500 m)范围内，风速分布有较大差别，随着海拔高度的继续增加，二者逐渐趋于相同.

［1］ 中交公路规划设计院.JTG/T D 60-01—2004公路桥梁抗风设计规范［S］.北京:中国标准出版社，2004.

［2］ 李永乐，唐康，蔡宪棠，等.深切峡谷区大跨度桥梁的复合风速标准［J］.西南交通大学学报，2010，45(2):167-173.LI Yongle，TANG Kang，CAI Xiantang，et al.Integrated wind speed standard for long-span bridges over deepcutting gorge［J］. Journal of Southwest Jiaotong University，2010，45(2):167-173.

［3］ 李永乐，张明金，徐昕宇，等.高海拔高温差深切峡谷桥址区日常大风成因［J］.西南交通大学学报，2014，49(6):935-941.LI Yongle，ZHANG Mingjin，XU Xinyu，et al.Causesof daily strong wind on bridge site in deep gorge withm high altitude and high temperature difference［J］.Journal of Southwest Jiaotong University，2014，49(6):935-941.

［4］ 刘红年，张宁，吴涧，等.水库对局地气候影响的数值模拟研究［J］.云南大学学报，2010，32(2):171-176.LIU Hongnian，ZHANG Ning，WU Jian，et al.Study of effects of reservoir on local climate using numerical simulation［J］.Journal of Yunnan University，2010，32(2):171-176.

［5］ BITSUAMLAK G T，STATHOPOULOS T，BEDARD C，et al.Numerical evaluation of wind flow over complex terrain:review［J］.Journal of Aerospace Engineering，2004，17(4):135-145.

［6］ CHOCK G Y K，COCHRAN L.Modeling of topographic wind speed effects in Hawaii［J］.Journal of Wind Engineering and industrial Aerodynamics， 2005，93(8):623-638.

［7］ KIM H G，PATEL V C，LEE C M.Numerical simulation of wind flow over hilly terrain［J］.Journal of Wind Engineering and industrial Aerodynamics，2000，87(1):45-60.

［8］ BITSUAMLAK G T，STATHOPOULOS T，EACUTE C B.Numerical evaluation of wind flow over complex terrain:review［J］.Journal of Aerospace Engineering，2004，17(4):135-145.

［9］ MURAKAMI S.Current status and future trends in computational wind engineering［J］.Journal of Wind Engineering and Industrial Aerodynamics， 1997，67/68(1):3-34.

［10］ XIAO Yiqing，LI Chao，LI Qiusheng，et al.Numerical simulation of wind speed distributions over complex terrains［C］∥ The 12th International Conference on Wind Engineering Caims.Australia:Australasian Wind Engineering Society，2007:1119-1126.

［11］ 邓院昌，刘沙，余志，等.实际地形风场CFD模拟中粗糙度的影响分析［J］.太阳能学报，2010，31(12):1644-1648.DENG Yuanchang，LIU Sha，YU Zhi，et al.Effect of roughness on CFD wind field simulation over natural terrain［J］.ACTA Energiae Solaris Sinica， 2010，31(12):1644-1648.

［12］ ABDID S， BITSUAMLAK G T. Wind flow simulationson idealized and real complex terrain using various turbulence models［J］. Advances in Engineering Software，2014，75(8):30-41.

［13］ 周志勇，肖亮，丁泉顺，等.大范围区域复杂地形风场数值模拟研究［J］.力学季刊，2010，31(1):101-107.ZHOU Zhiyong，XIAO Liang，DING Quanshun，et al.Numerical simulation study of wind environment for the flow around large region with complex terrain［J］.Chinese Quarterly of Mechanics，2010，31(1):101-107.

［14］ 李永乐，蔡宪棠，唐康，等.深切峡谷桥址区风场空间分布特性的数值模拟研究［J］.土木工程学报，2011，44(2):116-122.LI Yongle，CAI Xiantang，TANG Kang，et al.Study of spatial distribution feature of wind fields over bridge site with a deep- cutting gorge using numerical simulation［J］.China Civil Engineering Journal，2011，44(2):116-122.

［15］ 李永乐，遆子龙，汪斌，等.山区Y形河口附近桥址区地形风特性数值模拟研究［J］.西南交通大学学报，2016，51(2):341-348.LI Yongle，TI Zilong，WANG Bin，et al.Numerical simulation of wind characteristics over bridge site near Y-shaped river junction in mountainous area［J］.JournalofSouthwestJiaotong University， 2016，51(2):341-348.