基于加权秩和比法的隔震梁桥失效模式研究

张 云， 谭 平， 黄佳栋1，

(1.广西交通科学研究院有限公司，广西 南宁530007;2.广西翔路建设有限责任公司，广西 南宁 530007;3.广州大学工程抗震研究中心，广东广州510405)

20世纪90年代以来，我国的桥梁建设事业得到了迅猛发展，伴随计算机有限元分析技术的快速发展，有限元模拟手段在桥梁工程领域的应用也日益广泛［1-2］.基于以梁单元为主的宏观模型整桥分析是桥梁工程领域内有限元分析计算中的重要组成部分.通用有限元程序ABAQUS中的梁单元釆用的纤维梁模型是建立在材料本构基础上的，与集中塑性铰模型相比，它能更好地模拟梁单元的轴力-弯曲耦合滞回行为，精确性更高［3-4］.

目前，诸多学者对桥梁失效进行了研究，彭建新等研究了氯盐环境下RC简支梁桥的失效概率［5］;石雪飞评估了考虑空间变异性的在役钢筋混凝土梁桥的失效概率［6］.但这些研究均未对不同地震动作用下桥梁的失效模式进行统计分析，没有给出统计意义的失效模式以及桥梁的最弱失效模式.桥梁体系的失效是由结构构件逐步失效引起的，不同构件失效类型及失效顺序形成不同的失效模式，且失效路径并不唯一［7］.深入系统地研究连续梁桥地震作用下的失效模式，并对其进行控制，减小桥梁地震中的损伤，有利于震后快速恢复桥梁的功能，对减轻地震灾害和进行震后有效的抗震救灾具有重要的意义.

以某实际隔震连续梁桥为工程背景，采用修正的Park-Ang损伤模型研究了该桥梁的ABAQUS有限元模型在16种不同地震动作用下桥梁的失效模式，且通过加权秩和比的方法，给出具有统计意义的失效模式，并找出了桥梁的最弱失效模式.

1 工程概况及模型参数

分析模型为6跨110 m隔震连续梁桥，所有的桥墩均属于Ⅱ类墩身，1#～7#(从左往右)墩高分别为 23.7、23.4、23.8、23.5、23.1、23.1、23.7 m，桥梁宽度为33.1 m.桥梁下部构造由盖梁、墩柱以及连接两者的支座系统组成.墩柱为箱型柱式墩，长和宽分别为 10.0、3.5 m，厚度为 1.0 m，桥墩采用C50混凝土，HRB335钢筋，配筋率为 1.12%.承台的长、宽、高为 15.4、11.1、4.5 m.桥墩的基本结构尺寸以及纵向配筋示意图如图1所示.

采用ABAQUS有限元软件建立该桥的三维有限元模型，如图2所示.在对桥梁桩底纵向输入地震动时，取桥梁一侧支座作为研究对象并对连接单元编号为①～⑦，桥梁两侧的支座具有对称性，在纵向地震作用下，响应情况几乎一样，故本文仅取一侧支座作为研究对象.对于单柱墩的连续梁桥，桥墩柱的底部区域为塑性铰区域，取各墩墩底为研究对象，并对桥墩构件进行编号⑧～ 瑏瑤.

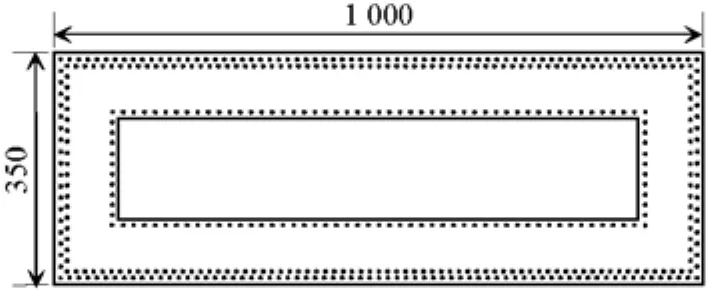
图1 桥墩截面(单位:cm)Fig.1 Details of piers(unit:cm)

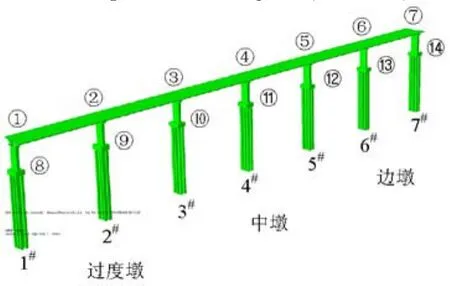
图2 桥梁三维有限元计算模型Fig.2 Three-dimensional finite element model of bridge

采用双折线弹塑性弹簧单元进行模拟铅芯隔震橡胶支座.桥梁采用的铅芯橡胶支座类型有LRB1250、LRB2500、LRB2750 3 种，桥梁各桥墩部分采用的LRB支座的详细参数如表1所示.

表1 LRB支座的参数Tab.1 Details of LRB

桥墩采用纤维梁单元，由于纤维梁单元需用子程序定义材料，而ABAQUS软件无法直接计算截面的剪切刚度，故将桥墩截面的剪切刚度设置为1×1016N/m.支座采用CONN3D2连接单元模拟，其他构件采用梁单元B31模拟，全桥共8 982个B31单元.采用m法算出土弹簧的刚度，用节点弹性支撑模拟桩-土的相互作用.

2 地震动的选取

地震动的选择对结构破坏的增量动力分析(incremental dynamic analysis，IDA)［8-11］结果影响很大，根据 Vamvatsikos和 Cornell的研究，在 IDA方法中采用15条地震动作为输入，足够反映地震动中存在的不确定性［12-13］.本文选取16条地震动对桥梁结构进行IDA分析，其对应的地震动加速度峰值(peak ground acceleration，PGA)分布在一个较宽的强度范围，如表2所示.

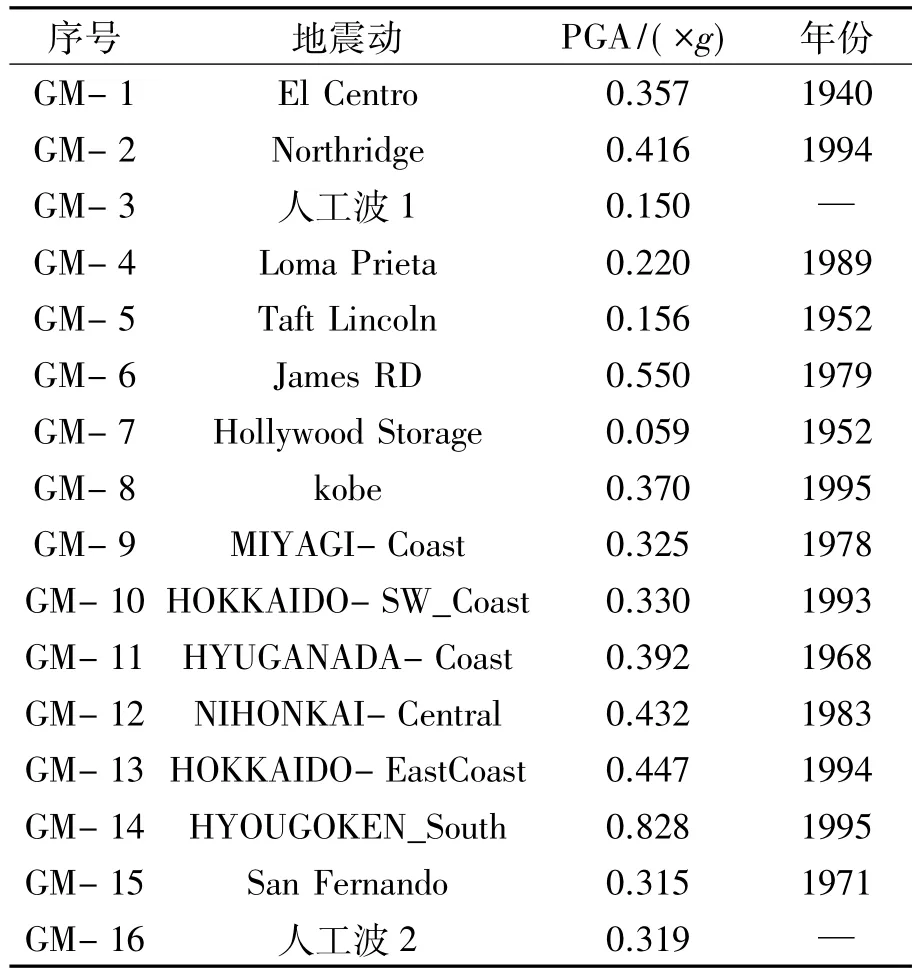
表2 选取的地震动参数Tab.2 Details of ground movements

3 桥梁的失效模式分析

3.1 LRB支座失效的判断

参照《公路桥梁抗震设计细则》(JTG/TB02-01—2008)，对铅芯橡胶支座进行验算时，在地震作用下产生的剪切应变应小于支座橡胶层厚度的2.5倍.《城市桥梁抗震设计规范》仅要求进行E2地震作用下的分析与验算，并要求橡胶型的隔震支座，在地震作用下产生的剪切应变应在250%以下，还要进行稳定性验算.本文采用的3种支座(LRB1250、LRB2750和 LRB2500)剪切变形为250%时的值分别为 715、630 mm 和 612.5 mm，并将其作为支座失效的判定值.

3.2 桥墩失效的判断

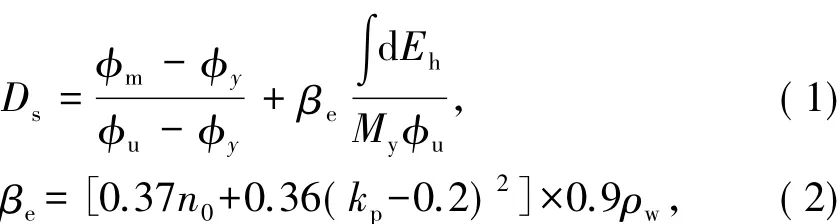
Stone和 Taylor［14］根据82个圆形桥墩的试验数据，在Park-Ang的损伤理论基础上进行了修改如式(1)、(2)［15］，并提出了新的损伤分级指标，见表3.式中:Ds为损伤参数;My、y为桥墩在静力单调荷载作用下的屈服弯矩和屈服曲率;m为桥墩在地震作用下的最大曲率;u为桥墩在静力单调荷载作用下的极限曲率;βe为组合参数;∫dEh为构件累计耗散的能量;n0为桥墩的纵向轴压比;ρw为体积配箍率;kp为归一化的受拉钢筋配筋率，kp=ρtfy/(0.85fc)，fy为钢筋抗拉屈服强度，fc为混凝土抗压强度，ρt为受拉钢筋配筋率.

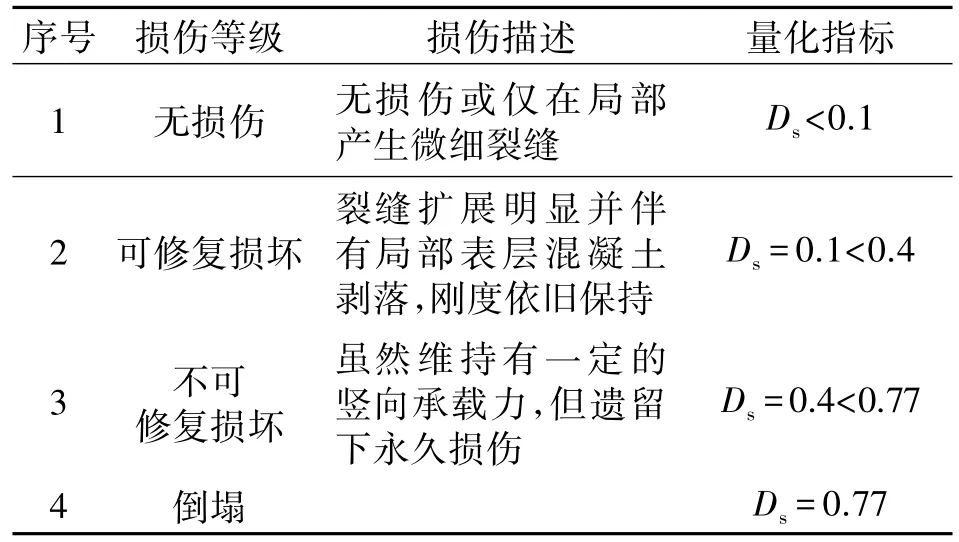
表3 修正Park-Ang构件损伤分级及参数Tab.3 Structural member classification and parameters of amendatory Park-Ang

3.3 桥墩能力参数的确定

可以通过MIDAS CIVIL软件求得桥墩截面屈服曲率y、屈服弯矩 My、极限弯矩 Mu、极限曲率u.截面的极限评估条件为:受压区混凝土应变首次达到εcu;截面抗弯能力下降到最大弯矩值的85%;计算点号输入50;计算得到桥墩截面各个参数如表4所示.

桥墩墩底截面纵向配筋如图1所示，桥梁墩底截面的M- 曲线如图3所示，图3中:Y为等效屈服曲率;U为极限曲率;Yc为初始屈服曲率.

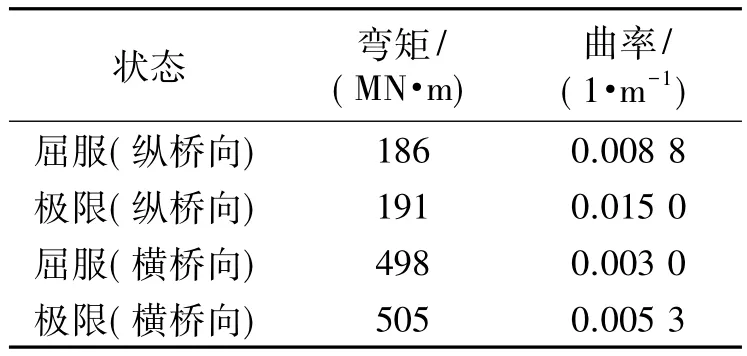
表4 桥墩的能力参数Tab.4 Capacity parameters of the pier

图3 桥梁墩底截面M- 曲线Fig.3 M- curves of the pier bottom

3.4 失效模式的统计分析方法

3.4.1 加权秩和比的统计分析方法

秩和比法是一种直观、有效的统计分析方法，且对资料无特殊要求，使用灵活简便，适用于统计资料的再分析［16］.此方法计算用的数值是秩次，可以消除异常值的干扰，它融合了参数分析的方法，结果比单纯采用非参数法更精确.秩和比法既可以对评价对象的优劣进行直接排序，还可以根据需要分档排序，而且引入各个指标的权重系数后得到的加权秩和比可以在一定程度上消除主观偏见，更具有客观与实际意义.为了找出桥梁的失效路径，本文统计出不同地震动作用下桥梁的失效模式，综合了16条地震动的评价信息，采用加权秩和比的统计分析方法分析了隔震连续梁桥在不同地震动作用下的失效模式.

秩和比法计算公式为［17］

式中:i=1，2，…，n;j=1，2，…，n;Rij为第 i行第 j列元素的秩.

当各个评价指标的权重不同时，计算加权秩和比W的公式为

且满足，

式中:Wj为第j个评价指标的权重.

3.4.2 结构体系的最弱失效模式

结构体系的失效模式可用事件集来描述，假设在失效模式事件集珔Ei中存在一个最大集

使得

从而得到

称对应于最大事件集珔Ei*的失效模式为体系的最弱失效模式.体系的最弱失效模式的工程意义在于要么失效模式珔Ei*伴随其它任何失效模式珔Ei出现，要么失效模式珔Ei*单独出现.

在单一随机源荷载Q确定性抗力的结构体系中，结构构件的极限状态方程可以表示为

相应的构件失效模式则为

结构体系的失效模式可表示为

式中:ni是结构第i个失效模式包含的失效构件数，ni≤n.

满足gi=，使得

设结构体系共有N个失效模式，则珔Ei*为

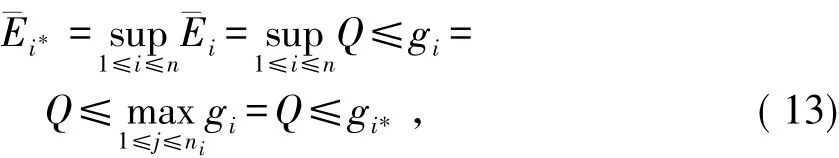
式中，满足

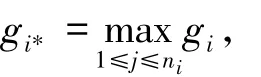
使得

4 失效模式的结果统计与分析

4.1 加权秩和比的统计结果分析

IDA方法现已广泛用于估计结构在遭遇不同强度地震动作用下的响应和分析结构的整体抗倒塌能力［17］.本文采用 IDA方法，根据改进的 Park-Ang损伤模型分析计算了隔震连续梁桥模型在16条地震动不同加速度峰值下各构件的损伤值，并根据损伤值的变化情况来确定各单元的失效顺序，分析结果如表5所示.

GM-1地震动作用下桥梁边墩支座失效后桥墩失效，是由于随着PGA的增大时，桥墩的失效时间将早于桥梁支座的时间，桥梁支座没有达到极限位移状态，仍然能传递上部结构的内力.其他地震动作用下，支座失效后桥墩仍然失效的原因与之类似.

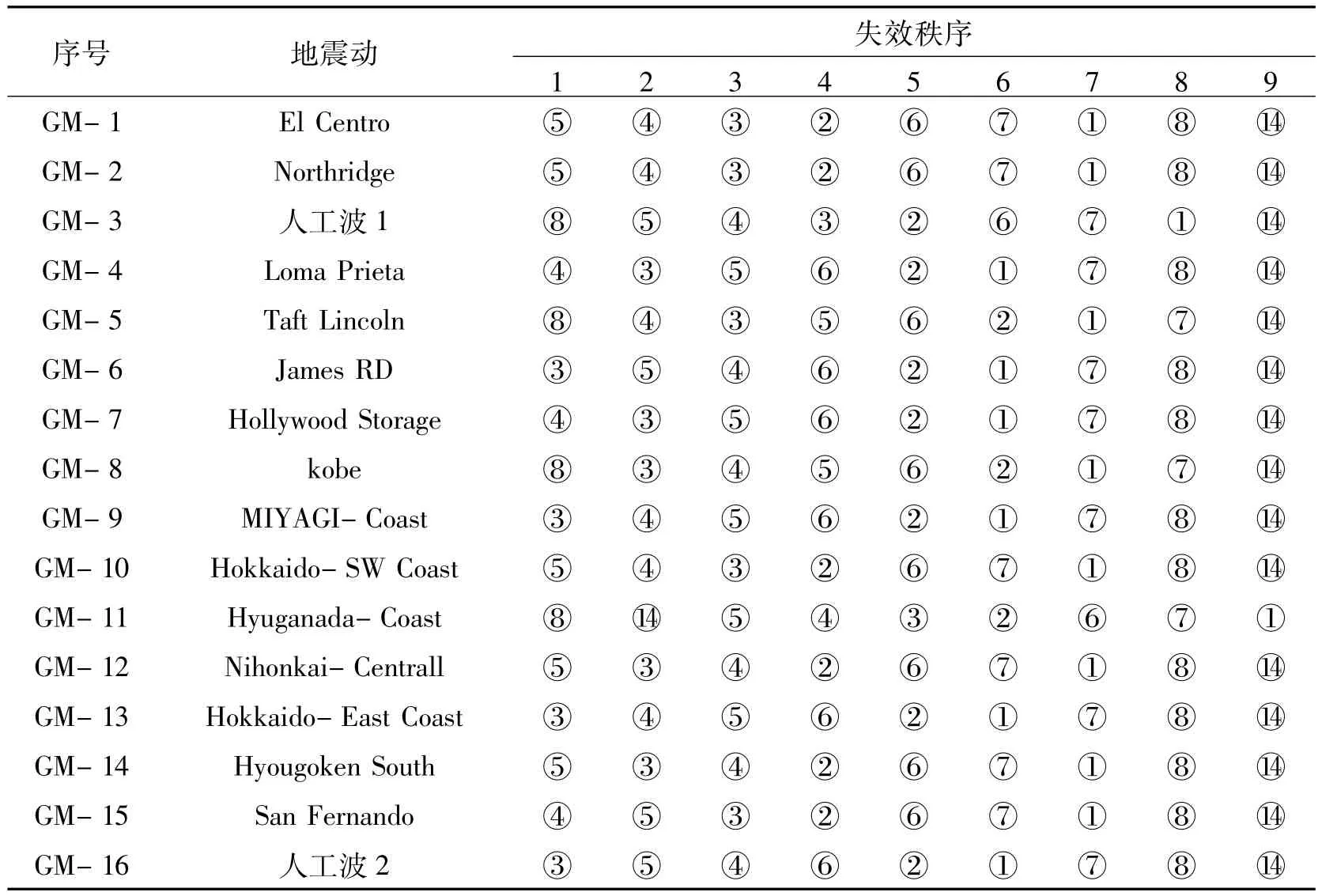
表5 各地震动作用下桥梁各单元的失效次序Tab.5 Failure sequence of bridge element in every ground movement

按照式(4)计算各地震动作用下桥梁出现的失效单元的加权秩和比，权重系数W取为该单元地震动的失效峰值加速度与所有地震动的失效峰值加速度总和的比值，并根据其先后失效顺序编秩.根据加权秩和比的大小，其数值越小，说明该构件越先失效，反之，构件失效越靠后.根据加权秩和比和失效顺序的对应关系，如表6所示.

由图6可得本工程隔震连续梁桥最终失效模式为:④→③→⑤→⑥→②→⑧→①→⑦→ 瑏瑤.即该桥梁中墩的隔震支座先失效，接着是桥梁过渡墩支座失效，然后是1#边墩底部和1#墩的支座失效，最后是7#边墩支座与7#桥墩墩底失效.

4.2 最弱失效模式分析

不同的地震动输入下结构各构件失效时，所对应的PGA均不同，且各构件的损伤量化指标Ds值的大小也不同.经过分析，在遭受强度较小的地震作用下，结构构件的Ds值先达到结构构件失效定义值0.75，结构构件最容易失效，即在 GM-7(hollywood storage)作用下桥梁失效模式为桥梁的最弱失效模式，如图4所示为构件在GM-7作用下，构件失效顺序及对应的PGA.

由图4知，桥梁最弱失效模式为:④→③→⑤→⑥→②→①→⑦→⑧→ 瑏瑤→ 瑏瑡→⑩→ 瑏瑢→ 瑏瑣→⑨.即首先是桥梁所有隔震支座先失效，其次是边墩底部失效，然后是中墩失效，最后是过渡墩失效.

桥梁在地震动GM-7作用下所有桥墩构件的最终失效模式如图5所示.

表6 失效单元的加权秩和比Tab.6 Rank-sum ratio of failure element

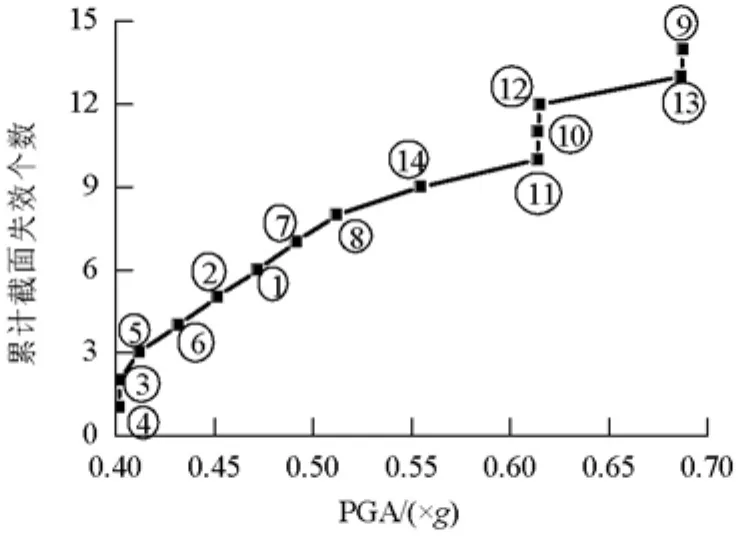
图4 桥梁构件失效顺序分布图Fig.4 Failure sequence of bridge component

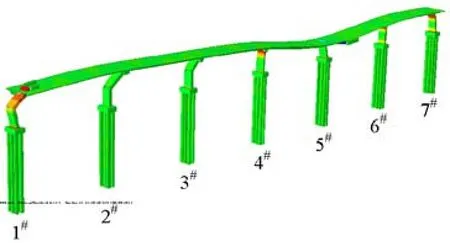
图5 桥梁最终失效模式Fig.5 Final failure mode of bridge

由图5可知，在强震作用初期，顺桥向桥墩所受惯性力最大，桥梁的边墩墩底率先形成塑性铰，而其他桥墩对整体桥梁结构顺桥向刚度的贡献比较小，所以桥梁1#墩先顺桥向倾斜，桥墩失效.随后桥梁结构的内力将重新分配，导致其他桥墩的内力将增大，受强震的持续作用，其他桥墩也陆续破坏，整体桥梁结构主梁沿桥梁顺桥向发生落梁，引起结构的整体倒塌.

5 结 论

基于ABAQUS软件的桥梁三维有限元模型，采用改进的Park-Ang模型，分析了隔震连续梁桥在16条地震动作用下结构的失效模式和最弱失效模式，得到如下结论:

(1)据损伤统计结果，对于跨径大，墩高大体一致的6跨隔震连续梁桥地震作用下的失效模式为:桥梁中墩的隔震支座先失效，接着是桥梁过渡墩支座失效，然后是1#边墩底部和1#墩的支座失效，最后是7#边墩支座与7#桥墩墩底失效.

(2)桥梁在GM-7作用下的失效模式为桥梁的最弱失效模式，桥梁最弱失效模式为:桥梁所有隔震支座先失效→边墩底部失效→中墩失效→过渡墩失效.桥梁的支座先失效，说明该桥梁的隔震设计比较合理，支座很好地起到了保护桥梁结构的作用.

［1］ 郑史雄，张金，贾宏宇，等.大跨度斜拉桥多维多点随机地震激励响应分析［J］.西南交通大学学报，2014，49(5):747-753.ZHENG Shixiong，ZHANG Jin，JIA Hongyu，et al.Stochastic seismic response analysis of large-span cable-stayed bridge subjected to multi-dimensional and multi-support excitations［J］.Journal of Southwest Jiaotong University，2014，49(5):747-753.

［2］ 聂建国，周萌，姬同庚，等.基于多尺度模型的自锚式钢箱梁悬索桥主缆锚固区受力性能研究［J］.土木工程学报，2014(6):57-69.NIE Jianguo，ZHOU Meng，JI Tonggeng，et al.Study on behaviors of cable anchorage zone of self-anchored suspension bridges with steel box girders based on multiscale modeling method［J］.China Civil Engineering Journal，2014(6):57-69.

［3］ 徐小龙.基于ABAQUS纤维梁元的静力弹塑性分析［D］.成都:西南交通大学，2012.

［4］ 强斌，李亚东，顾颖，等.钢板喷丸处理残余应力场和表面粗糙度数值模拟［J］.西南交通大学学报，2015，50(4):691-697.QIANG Bin，LI Yadong，GU Ying，et al.Numerical simulation of residual stress field and surface roughness for steel plate subjected to shot peening［J］.Journal of Southwest Jiaotong University，2015，50(4):691-697.

［5］ 彭建新，胡守旺，张建仁.考虑空间变量的氯盐环境下RC简支梁桥失效概率分析［J］.土木工程学报，2014(12):115-121.PENG Jianxin， HU Shouwang， ZHANG jianren.Analysis on failure probabilities of RC simply-supported beam under Chloride environment with spatial variables considered［J］. China Civil Engineering Journal，2014(12):115-121.

［6］ 石雪飞，王晓明，阮欣，等.考虑空间变异性的在役钢筋混凝土梁桥失效概率评估［J］.土木工程学报，2011(6):74-79.SHI Xuefei， WANG Xiaoming， RUAN Xin， et al.Failure probability assessment of existing RC beam bridges considering spatial variability［J］.China Civil Engineering Journal，2011(6):74-79.

［7］ 刘梦莹，徐岳.基于失效树的连续刚构桥体系可靠度研究［J］.合肥工业大学学报:自然科学版，2014(11):1341-1345.LIU Mengying，XU Yue.Research on the reliability of continuous rigid frame bridge system based on failure tree［J］.Journal of Hefei University of Technology:Natural Science，2014(11):1341-1345.

［8］ MANDER J B，DHAKAL R P，MASHIKO N，et al.Incrementaldynamic analysis applied to seismic financial risk assessment of bridges［J］.Engineering Structures，2007，29(10):2662-2672.

［9］ BILLAH A H M M，ALAM M S.Seismic performance evaluation of multi-column bridge bents retrofitted with different alternatives using incremental dynamic analysis［J］.Engineering Structures，2014，62:105-117.

［10］ WANG G，WANG Y，LU W，et al.XFEM based seismic potential failure mode analysis of concrete gravity dam-water-foundation systems through incremental dynamic analysis［J］. Engineering Structures，2015，98:81-94.

［11］ 周颖，苏宁粉，吕西林.高层建筑结构增量动力分析的地震动强度参数研究［J］.建筑结构学报，2013，34(2):53-60.ZHOU Ying，SU Ningfen，LU Xilin.Study on intensity measure of incremental dynamic analysis for high-rise structures［J］.Journal of Building Structures，2013，34(2):53-60.

［12］ VAMVATSIKOS D，CORNELL CA.Incremental dynamic analysis［J］. Earthquake Engineering ＆Structural Dynamics，2002，31(3):491-514.

［13］ 于晓辉.钢筋混凝土框架结构的概率地震易损性与风险分析［D］.哈尔滨:哈尔滨工业大学，2012.

［14］ STONE W C，TAYLOR A W.Seismic Performance of circular bridge columns designed in accordance with AASHTO/CALTRANS standards［R］.Gaithersburg:National Institute of Standards and Technology，1993.

［15］ 郭进，王君杰.基于累积损伤的弯矩-曲率强度退化滞回模型［J］.同济大学学报:自然科学版，2013，41(12):1767-1774.GUO Jin，WANG Junjie.Reinforced concrete strength degradation hystertic moment-curvature mode based on cumulative damage［J］. Journal of Tongji University:Natural Science，2013，41(12):1767-1774.

［16］ 李伟伟，李洪兴，王卫，等.基于加权秩和比法的农村水厂风险评估［J］.环境与健康杂志，2014，31(10):934-937.LI Weiwei，LI Hongxing，WANG Wei，et al.Risk assessment of rural waterworks by weighted rank sum ratio method［J］.Journal of Environment and Health，2014，31(10):934-937.

［17］ 刘耀龙.强震作用下结构连续倒塌过程中的失效模式研究［D］.大连:大连理工大学，2013.