机械臂力跟踪阻抗和避碰控制仿真研究

汪 双 ，刘满禄 ，2，张 华

（1.西南科技大学 特殊环境机器人技术四川省重点实验室，绵阳 621010；2.中国科学技术大学 信息科学技术学院，合肥 230026）

随着机器人技术的不断提高以及应用领域的不断扩展，作为机器人重要代表之一的机械臂也趋于适应更多的应用场合，当前机械臂更是迫切需要应用于非结构化的作用环境[1]，打磨、抛光、组装等接触性任务不但要求机械臂末端工具能以适当力接触工件表面，同时要求机械臂能够沿着工件表面相对移动[2]，这对机械臂的柔顺性和安全性提出了更高的要求。机械臂柔顺控制和占据机械臂安全问题主导地位的避碰控制技术一直是国内外的研究热点。

文献[3]提出的阻抗控制是机械臂主动柔顺控制的重要部分；文献[4]基于位置控制内环的阻抗控制更是确保了非接触状态下的位置跟踪精度；文献[5]基于力/位混合控制实现了机械臂末端工具在对象弧形表面的柔性接触，但其控制结构较之阻抗控制更为复杂；文献[6-7]基于自适应混合阻抗控制实现了机械臂在环境表面的稳定接触力运动；文献[8]在未知环境信息下实现力跟踪阻抗控制则更为简单；文献[9-11]利用广义动量观测器进行碰撞力估计，但其准确度容易受到较大加速度的影响。

综合以上方法优缺点，为了解决机械臂力跟踪阻抗控制和安全避碰问题，本文基于图1所示的二自由度平面机械臂，建立其运动学动力学模型，设计操作空间线性解耦位置控制器，结合位置控制内环以及力跟踪阻抗控制，实现机械臂在操作空间阻抗控制方向上作用力的稳定；同时在位置控制方向上，基于作用合力方向的直线运动控制，确保位置控制的安全避碰；文章最后基于Simulink-Adams联合仿真，验证了力跟踪阻抗控制和避碰控制的有效性。

图1 二自由度平面机械臂Fig.1 2 DOF plane robot manipulator

1 机械臂运动学动力学分析

1.1 运动学分析

图2所示为二自由度平面机械臂运动学模型，对其第一、二关节以及末端工具处建立参考坐标系，基坐标系（x，0，y）与第一关节参考坐标系（x0，0，y0）初始位置重合。

图2 机械臂运动学模型Fig.2 Kinematics model of robot manipulator

图 中 ：m1、m2、l1、l2、a1、a2、θ1、θ2分 别 为 连 杆 1、2的质量、长度、重心距离前一关节长度以及关节角度；r为末端工具到基坐标系原点距离；（x，y）为末段工具相对基坐标系的位置，其正运动学为

由式（1）～式（3）以及余弦定理可知其逆运动学为

式中，±分别对应机械臂同一末端位置的2种构型。

1.2 动力学分析

式中：M，V，G分别为惯性、科氏力向心力以及重力矩矩阵；u为作用在机械臂关节上的广义力矩；f为环境作用在末端工具上的广义力；J为雅克比矩阵。假设为末端工具笛卡尔速度，则：

2 位置内环阻抗控制器

2.1 环境模型

环境施加在机械臂上的作用力f通常用弹簧模型来表示：

式中：f为环境作用力，当机械臂未与环境接触时f为零；x，xe分别为机械臂位置以及环境静态位置；Ke为环境刚度。

2.2 操作空间线性解耦位置控制器

关节空间基于非线性补偿的线性解耦控制律[13]为

式中，α为需要设计的控制输入，结合式（8）且机械臂未与环境接触（f=0）：

假设J非奇异，由式（10）可得：

式中，Kd，Kp为对称正定的增益矩阵，结合式（12）～式（15）得操作空间线性解耦控制器为

若 f=0 且 e=xd-x，将式（16）代入式（8）得闭环控制律：

因Kd，Kp均正定，可知误差均为0。

2.3 位置内环阻抗控制器

机械臂与环境接触时，如果只对机械臂施加位置控制，由式（11）可知作用力会逐渐增大，进而损坏机械臂末端工具或环境。阻抗控制则能实时依据作用力并调整参考轨迹，以使机械臂与环境之间呈现如下动态关系：

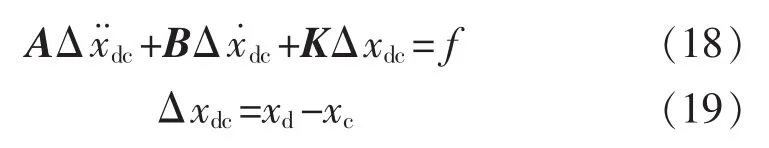
式中：A，B，K分别为惯性、阻尼和刚度系数对角矩阵，其定义了机械臂与环境接触时的动态行为特性；xd，xc分别为参考位置和阻抗调整后位置。因A，B，K为对角矩阵则式（18）关系解耦，则单一操作空间自由度阻抗动态特性如图3所示。

图3 阻抗动态特性Fig.3 Dynamic characteristics of impedance

图中：ai，bi，ki为 A，B，K 对角元素；c，c，xc分别为调整后的操作空间参考加速度、速度和位置，再结合式（16）位置控制器形成位置内环阻抗控制器。

结合图3可知机械臂位置输出X（s）与参考位置 Xd（s）之间特征方程为

可知阻尼比为

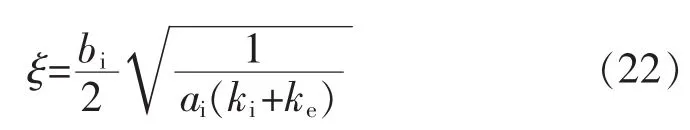
由于环境刚度 ke远大于 ai，bi，ki，系统很容易处于欠阻尼状态，由式（22）可知应适当增大阻尼系数bi，同时减小质量、刚度系数 ai，ki，以获得期望的系统阻尼。

3 力跟踪阻抗控制器

通过图3可以看出环境静态位置和刚度决定了反馈作用力f。理论上说，如果能够确切获悉环境位置和刚度，通过轨迹规划和阻抗控制也可以实现期望作用力，然而实际上很难做到这一点。

假设xr为依据环境位置设定的初始参考轨迹，xr确保机械臂能与环境接触即可；fr为参考作用力，ri为轨迹调整系数。通过Δxr调整xr获得阻抗控制参考位置：

结合位置控制器，参考位置xd驱使作用力f趋于参考作用力 fr。 忽略力跟踪阻抗控制结构如图4所示。

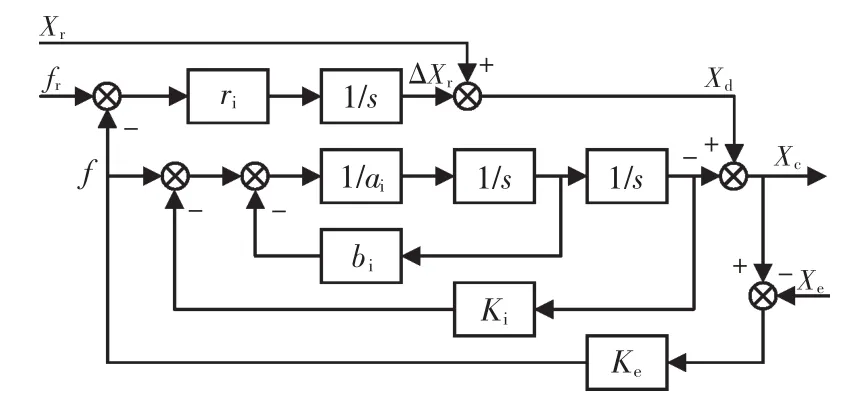
图4 力跟踪阻抗控制结构Fig.4 Structure of force tracking impedance control

分别定义作用力误差和二次误差函数：

稳态时由式（18）、（19）可知：

结合式（20）的假设和式（11）可知稳态时[4]：

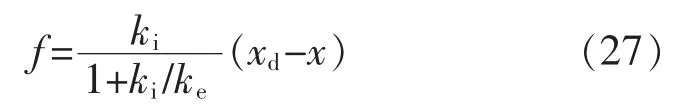
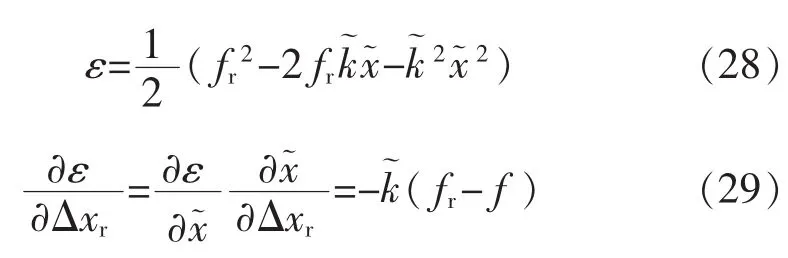
根据梯度下降法可知，误差函数ε沿着：

迭代收敛到最小值，λ为迭代步长或采样周期，此时 f→ fr，同时 xr沿着 Δxr变化方向使 xr→xd：

令 ri=λ，对式（31）拉氏变换：

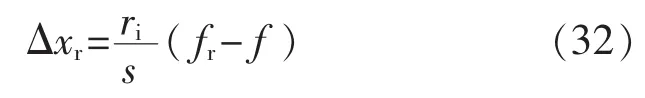
依据式（20）的假设，由图4可知机械臂位置输出与参考作用力fr（s）的闭环特征方程为

由劳斯判据可知系统稳定的条件为

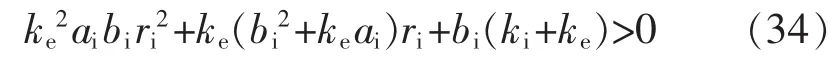
由于式（34）中系数均大于0，故任意ri＞0式（34）肯定成立，系统稳定。实际可以取较小的ri，使得作用力跟踪性能更好[10]。

4 避碰控制器

机械臂操作空间位置控制自由度方向上，末段工具沿着环境表面运动甚至与障碍碰撞时，当作用力大于一定阈值，则可能损坏末端工具或环境。若能够实时检测作用力，且在作用力超过一定阈值时控制机械臂向作用力瞬速衰减方向运动，则机械臂和环境的安全性将得到很大的保障。图5为机械臂与环境接触示意。

图5 机械臂与环境接触示意Fig.5 Sketch map of the contact between robot manipulator and environment

由图5可见，当机械臂沿着环境表面运动时，此时fxy1为作用力合力；当机械臂与障碍碰撞时，此时fxy2为作用力合力。可以发现，作用力合力方向正好是避免机械臂与环境过度接触的最佳撤退方向。假设fx，fy分别为环境对机械臂沿着x，y轴方向作用力，则撤退方向单位矢量为

若机械臂当前位置为x，期望撤退位置为xf，d为撤退距离系数，则：

将式（15）控制律稍作修改[14]：

此时式（16）的控制律将使机械臂以笛卡尔速度Vmax直线运动到期望撤退位置xf。

设定作用力阈值为 Fg=（Fgx，Fgy），若条件判断（fx＞Fgx）‖（fy＞Fgy）成立，则机械臂由力跟踪阻抗控制切换到避碰控制。

5 仿真验证

在Adams中建立机械臂仿真模型如图6所示，右边为曲形表面环境模型。

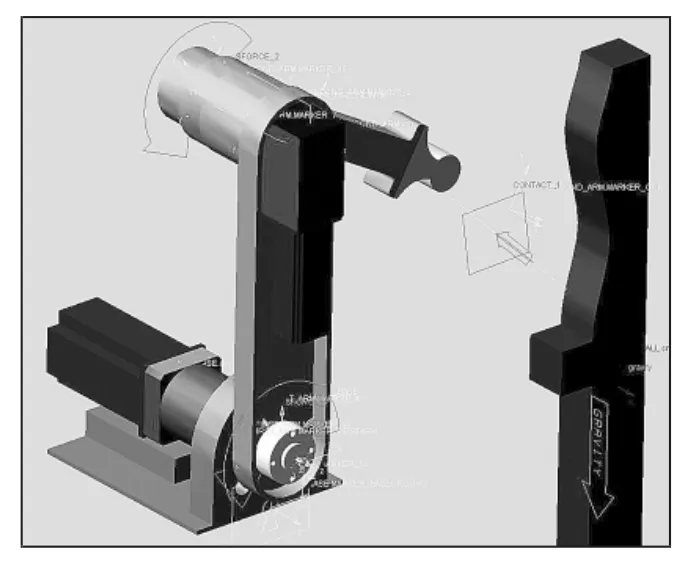
图6 Adams仿真模型Fig.6 Adams simulation model

图7为机械臂参考轨迹图。其中，连杆1、2的质量分别为m1=4.85 kg，m2=1.22 kg；长度分别为l1=0.350 m，l2=0.355 m；重心距离分别为 a1=0.250 m，a2=0.160 m；连杆 1的转动惯量为 I1x=0.07807 kg·m2，I1y=0.07302 kg·m2，I1z=0.01056 kg·m2； 连杆 2 的转动惯量为 I2x=0.02034 kg·m2，I2y=0.02018 kg·m2，I2z=0.00044 kg·m2；环境刚度 Ke=105N/m；重力沿 y轴负方向，G=9.81 N/kg。

图7 机械臂参考轨迹Fig.7 Reference trajectory of robot manipulator

Simulink仿真控制结构如图8所示，轨迹调整部分实时调整参考轨迹，生成中间参考轨迹提供给位置内环阻抗控制器；作用力未超过阈值时阻抗控制器接管控制，作用力超过阈值时，避碰控制器Switch有效并接管控制。其中参考力fr=10 N；轨迹调整系数ri=0.06；阻抗控制器惯性、阻尼以及刚度系数矩阵分别为 A=［5，5］，B=［3000，3000］，K=［50，50］；内环 位 置 控 制 器 参 数 分 别 为 Kd=［500，500］，Kp=［2000，2000］；避碰控制器参数 Kd=［500，500］；撤退距离系数d=0.1；撤退速度Vmax=0.03 m/s；接触力阈值 Fg=［30，30］N。

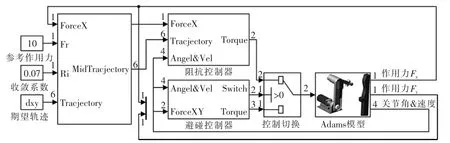
图8 Simulink仿真控制结构Fig.8 Control structure of Simulink simulation

图9为Adams仿真动态图，当时t=9.1 s，机械臂末端工具与环境开始接触，然后沿着环境表面向下运动；当t=19.5 s时，机械臂末端工具与障碍发生碰撞；当t=20.3 s时，作用力超过阈值而触发避碰控制器，机械臂开始远离环境；当t=24.0 s时，机械臂撤退到安全位置。

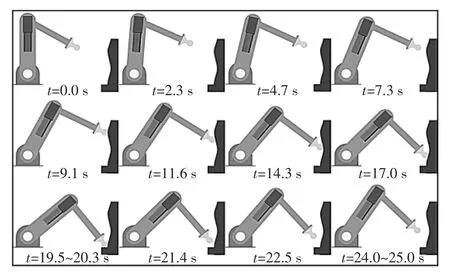
图9 Adams仿真动态图Fig.9 Dynamic graphs of Adams simulation

机械臂期望轨迹和实际轨迹如图10所示，可见位置内环阻抗控制确保了非接触时的位置跟踪，同时由于末端工具参考点位于半径r=0.02 m的圆形接触体中心，因此接触时实际参考轨迹相比环境接触表面偏左0.02 m。

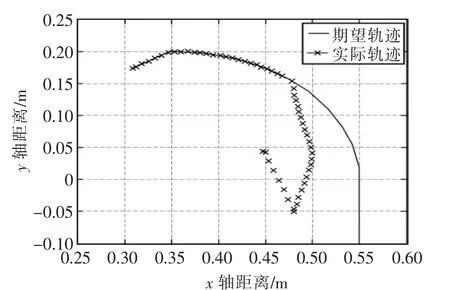
图10 期望轨迹和实际轨迹Fig.10 Desire trajectory and actual trajectory

机械臂x轴方向上的作用力以及误差如图11所示，可见机械臂与环境接触时，力跟踪阻抗控制能够迅速维持作用力f=10 N；但在t=15 s左右时，作用力出现波动，此时末段工具处于接触面最凹处，接触面对机械臂作用力变化比较大，这一点通过图12机械臂y轴方向作用力在t=15 s时的快速变化可以看出；t=19.5 s时，机械臂与障碍发生碰撞，x轴作用力出现波动，y轴作用力迅速上升；直至t=20.3 s时，y轴作用力达到阈值30 N，避碰控制器触发，x、y轴作用力迅速降为0，机械臂撤退到安全位置；避碰触发瞬间可以发现x轴作用力出现波动，这是由于控制切换瞬间，x轴阻抗特性瞬间丢失，同时位置控制需要一定的时间去收敛。

图11 x轴作用力和误差Fig.11 Reaction force in x-axis and force deviation

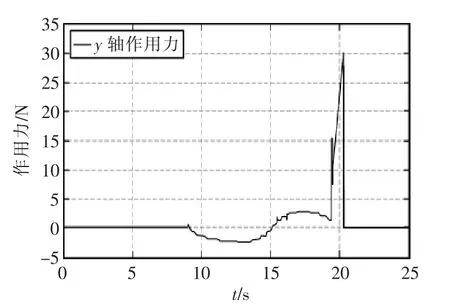
图12 y轴作用力Fig.12 Reaction force in y-axis

6 结语

本文在位置内环阻抗控制的基础上，基于作用力误差实时调整参考轨迹的力跟踪方式，实现了机械臂在操作空间x轴方向的作用力恒定；同时基于操作空间y轴方向的位置控制，依据作用合力方向直线位置运动的避碰控制原理，实现了机械臂在非阻抗控制方向上的安全保障。本文基于比较简单的二自由度机械臂进行了柔顺性和安全性分析，然而实际生产中广泛应用的六自由度机械臂，涉及姿态以及扭矩等更复杂的柔顺相关问题以及机械臂本体避碰问题；其次，接触面的摩擦力以及实际环境模型可能涉及到基于刚度系数的指数级变化，甚至包括阻尼特性，这些问题将是接下来的研究深入点。

[1]A.De Luca，R.Mattone.Sensorless robot collision detection and hybrid force/motion control[C]//Proceeding of the 2005 IEEE International Conference on Robotics and Automation，2005：18-22.

[2]李二超，李战明.基于力/力矩信息的面相位控机器人的阻抗控制[J].控制与决策，2016，31（5）：957-956.

[3]N.Hogan.Impedance control：an approach to manipulation[J].ASME J.Dyna.Syst.，Measure.，Control，1985（107）：1-24.

[4]Bruno Siciliano，Luigi Villani.Robot Force Control[M].New York：Kluwer Academic Publishers，1999：31-43.

[5]L.Hu，J.Zhan.Study on the orthomogonalization for hybrid motion/force control and its application in aspheric surface polishing[J].The InternationalJournalofAdvanced Manufacturing Technology，2015，77（5）：1259-1268.

[6]L.F.Baptista，JMGSD Costa.Adaptive hybrid impedance control of robot manipulators：a comparative study[C]//Proceedings of the 1997 OE/IFIP/IEEE International Conference on Integrated and Sustainable Industrial Production，Lisbon，1997：177-187.

[7]S.Jung，T.C.Hsia，RG Bonitz.Force tracking impedance control of robot manipulators under unknow environment[J].IEEE Transactions on Control Systems Technology，2004，12（3）：474-483.

[8]T.A.Lasky，T.C.Hsia.On force-tracking impedance control of robot manipulators[C]//Proceedings of the 1991 IEEE International Conference on Robotics and Automation，1991（1）：274-280.

[9]E.Magrini，F.Flacco，A.De Luca.Estimation of contact forces using a virtual force sensor[C]//Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems，2014：2126-2133.

[10]E.Magrini，F.Flacco，A.De Luca.Control of generalized contact motion and force in physical human-robot interaction[C]//Proceedings of the 2015 IEEE International Conference on Robotics and Automation，2015：2298-2304.

[11]A.De Luca，R.Mattone.Sensorless robot collision detection and hybrid force/motion control[C]//Proceedings of the 2005 IEEE International Conference on Robotics and Automation，2005：999-1004.

[12]Frank L.Lewis，Darren M.Dawson，Chaouki T.Abdallah.Robot Manipulator Control Theory and Practice[M].New York：Marcel Dekker，Inc.，2004：107-126.

[13]Bruno Siciliano，Lorenzo Sciavicco，Luigi Villani，Giuseppe Oriolo.Robotics：Modelling，Planning and Control[M].London：Springer Science and Business Media，2010：327-348.

[14]Oussama Khatib.A unified approach for motion and force control of robot manipulators：the operational space formulation[J].IEEE Journal on Robotics and Automation，1987，3（1）：43-53.