基于L-M优化算法的学分绩点预测模型构建

王 涛，潘和平，蔡成梅

(1.安徽建筑大学 教务处，安徽 合肥 230601； 2.合肥师范学院 教务处，安徽 合肥 230601)

1 引言

随着计算机大数据存储技术在高校深入应用，学生的成绩实现了电子形式的完整保存，但大量的成绩数据却没得到很好的利用。对于每个学生来讲，仅能查询到自己的目前成绩，无法知道自己当前学习状态及将来学习成绩的趋势。对于教学管理者，仅是通过个人的工作经验对学生进行指导，无可以支持的数据，无法提供有效合理的学习建议。因此，学业预警已经成为高校学生管理的热点，然而学业预警的难点是发现科学、有效和精准的学分绩点预测方法。本文利用计算机存储的学生历史成绩数据和课程之间关系，构建了基于神经网络的学分绩点预测模型，经过数据对比测试，发现利用L-M优化算法的预测模型结果与实际情况符合度最高，能够应用于学生学业预警。

2 课程与学分绩点

2.1 学分绩点

根据我校教学管理规定，本科生授予学士学位其中一个重要标准是当学生完成学业时需平均学分绩点学达到1.8。平均学分绩点为课程学分绩点总数除以修读的课程学分总数[1]，其计算公式为：

平均学分绩点=∑课程学分绩点/∑课程学分=∑(课程绩点×课程学分)/∑课程学分

2.2 课程之间关系

学校制定教学培养方案时，不仅规定了课程类型和性质，而且设置了课程开课顺序。因此，学生在学习选课的时候，需要了解课程间的内在联系和课程间的前导后继关系。我校土木工程专业的通识课程和专业基础课程是专业的主干和核心课程，需在前四个学期完成，这些课程之间彼此联系，同时又是其他课程的前导课程。例如，高等数学A1和高等数学A2之间是前导后续关系，高等数学A1学习结果直接影响高等数学A2，同时他们又一起影响大学物理B的学习，而大学物理B又会关系到理论力学、材料力学A、结构力学专业基础课程的学习，因此，课程之间有明显的层次和网络关系。

2.3 课程和学分绩点之间关系

学生最终学业平均学分绩点是所在专业全部修读课程的学分累积。所有的课程彼此紧密相关，当一门课程是其他课程的前导课程时，如果该课程成绩不理想，后续课程成绩将会受到影响，最终学分绩点比较低。表1是我校土木工程专业某位学生部分通识教育和专业主修课程成绩表，发现其前期主干课程未获得较好成绩，随后相关联课程成绩都不理想。

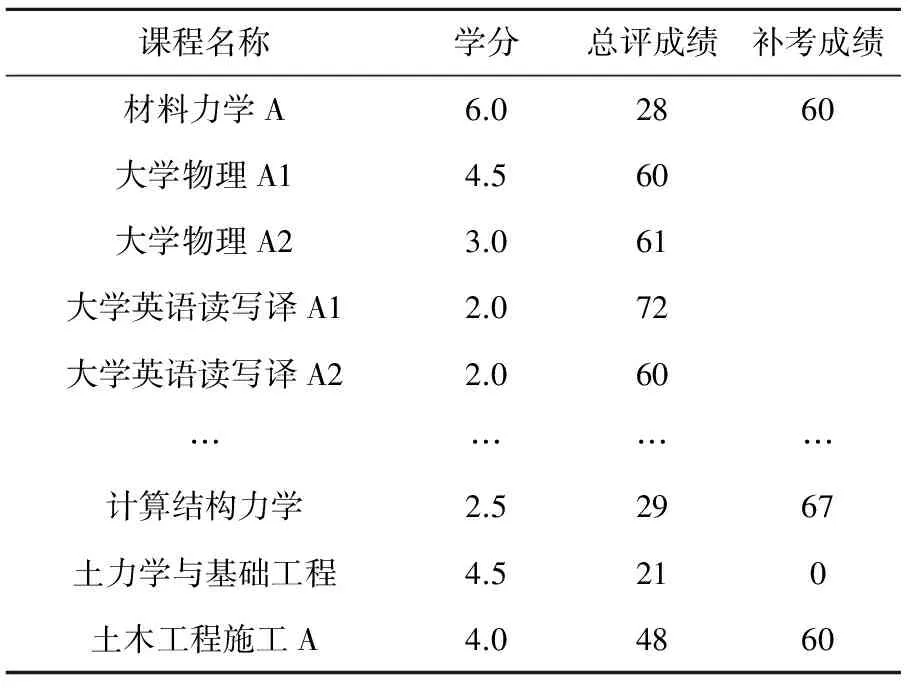
表1 某学生考核成绩表

2.4 学分绩点预测方法

课程与课程之间、课程及学分绩点之间的联系非常紧密，因此构建课程与课程之间、课程及学分绩点之间的关系模型，确定课程间的关联系数，我们就可以根据前导课程的成绩和绩点预测后续课程成绩和学分绩点，从而在学生学习进程中间进行预测、警示。具体方法如下：

设预测一个学生某门课程Bn的成绩和绩点：

其前导课程为：A1,A2,…An;

Bn关于A1,A2,…An的关联系数向量为：β=β1,β2,…,βnT；

待测学生的课程A1,A2,…An的成绩为：S1,S2,…Sn；

事实上在实际预测的时候，这种方法存在诸多问题，一方面，一定要求前导课程的成绩S1,S2,…Sn中不能有缺失项；另一方面，需要确定课程相关性，弄清所有课程间的“前导后继”关系，构建所有课程之间的关系图表；其次，需要准确设定课程之间的关系系数取值。但是这些都是非常困难的，利用课程关联系数预测学分绩点的模型是有局限性，因此可以借助机器学习工具来模拟学分绩点预测模型[2]。

3 学分绩点预测模型确定

3.1 学分绩点预测模型的构建

学生完成学业后最终的平均学分绩点，是将全部修读课程的学分进行累计核算的，如果在学习过程中提前预测每个学生平均学分绩点，采用上述的课程关联系数模型，就需要预测未学习的课程成绩，而BP神经网络特点能够适应学分绩点统计过程中，课程之间存在着相互关联的关系，非常适合进行学分绩点的预测。

模型的确定

(1)输入、输出的确定

学分绩点预测模型的具体设计是：每学期所学习课程成绩S1,S2,…Sn作为输入项，完成学业后最终的平均学分绩点Gn结果作为输出项，模型学习训练后，得到每学期课程成绩与平均学分绩点之间的关系。对于待预测学生，将已获得学分的课程成绩作为输入，经过训练好的绩点预测模型，可以得到该学生完成学业后最终的平均学分绩点[3]。

(2)隐含层的确定

在BP神经网络中，对于隐含层节点数的确定是难点也是重点。如果隐含层节点数过少，将会导致网络性能不好甚至无法训练；如果隐含层节点数过多，能够减小神经网络的系统误差，但是增加了网络训练时间，导致局部极小点，使网络的容错性、泛化能力变弱。所以，选择准确的隐含层节点数是非常重要的。因网络的输入层和输出层是课程成绩和学分绩点，这两层的节点数一般是相对固定的，不能随意改变，所以整个网络结构中需要确定的是隐含层的层数及其节点数目。通常，根据以下几个经验公式进行三层BP网络的隐含层节点数的确定[9]。

1)k=n-1，其中n为输入层节点数；

2)k=log2n，其中k为隐含层节点数，n为输入层节点数；

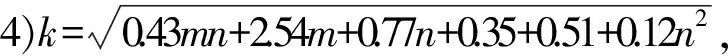
假设输入层节点数n=10，输出层节点数m=1，则根据经验公式可知隐含层节点数k为4至13 之间，然后在神经网络中分别进行训练实验，以确定隐含层节点数目，选取最大训练次数5000次，固定目标函数(均方误差)为0.001来开始实验，训练实验结果具体如下：

表2 隐含层节点数

根据表2实验结果，当BP网络的隐含层神经元个数为9时，其对函数的逼近效果达到最好，因为它的误差最小[5]。

3.2 数据预处理

①输入数据处理

教学计划中每门课程的成绩真实反映了学生的该门课程学习情况，因此模型采用课程成绩作为输入。模型训练的输入数据需要归一化处理，本文是利用下面的公式：

其中x为课程成绩，xmin是课程成绩最小值，一般为0；xmax是课程成绩最大值，一般为100；P是课程成绩归一化后在(0, 1)之间的值。

②输出数据处理

模型采用平均学分绩点作为模型输出，对我校教学管理系统中的数据库进行分析，成绩数据库包含了每位学生所选课程的学分、成绩及绩点，根据这些数据和绩点计算公式可以计算出学生的平均学分绩点。 本文是利用下面的公式对模型的输出数据进行归一化在[0,1]之间：

其中y为平均学分绩点，ymin是平均学分绩点最小值，一般为0；ymax是课程成绩最大值，一般为5；T是课程成绩归一化后在(0, 1)之间的值。

4 模型创建、训练与测试

4.1 模型的创建

本文使用MATLAB7．1神经网络工具箱进行具体预测系统的实现，采用NEWFF函数创建10×9×1的三层BP神经网络结构，其中输入层有10个神经元，中间隐含层有9个神经元，输出一个结果，如图1。神经网络的输入层、隐含层神经元设定为双曲线正切S型传递tansig函数，输出结果归一化到[0,1] 之间，输出层神经元的传递函数设定为对数S型传递logsig函数[6]。

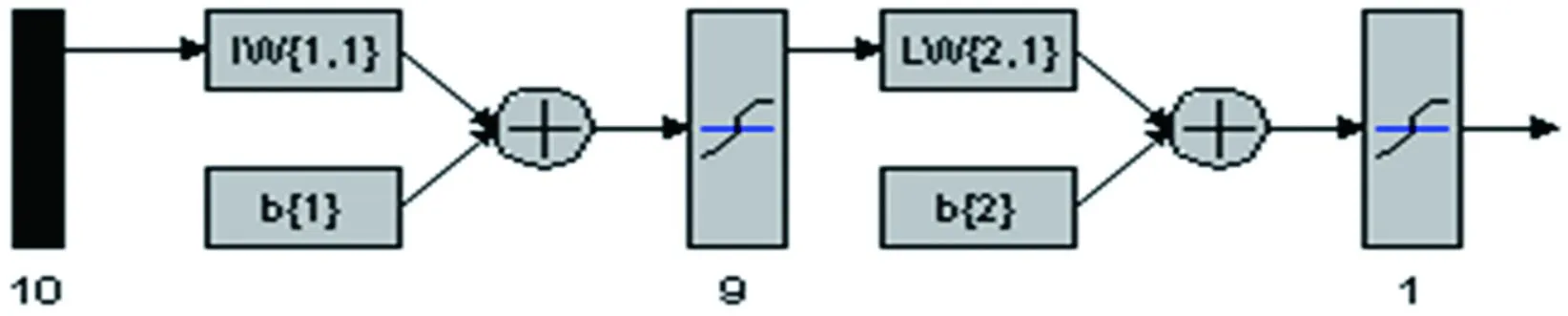
图1 神经网络结构

4.2 模型的训练

1.模型的实现

MATLAB7．1程序提供了函数变量工作区workspace，workspace用于保存当前计算的变量和结果变量。工作区浏览器采用可视化的图形用户界面，用户不仅能够查询和管理MATLAB工作空间的内容，还可以执行与clear, load, open, and save 函数同样的功能。

MATLAB支持工作区的保存。用户可以通过文件的形式保存工作区或工作区中的变量，当需要时可以再次导入数据。保存工作区有两种方式：菜单选择和窗口命令执行[10]。

变量工作区workspace进行输入、输出数据矩阵的创建，如图2。

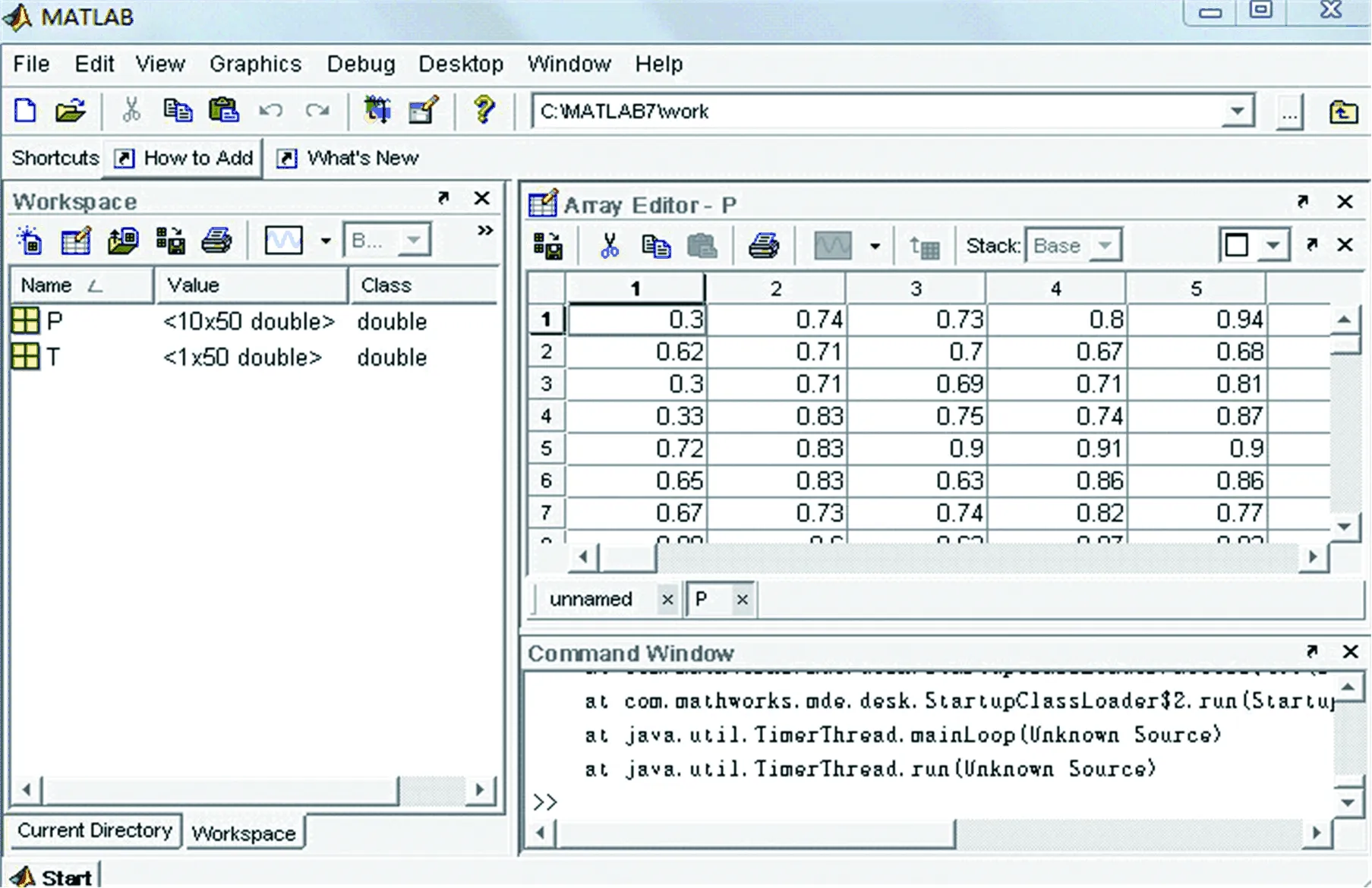
图2 输入、输出数据矩阵的创建

模型实现的MATLAB程序代码：

>>clear all;

%网络创建

net = newff(minmax(P),[10,1],{'tansig' 'logsig'},'trainlm');

%网络参数设置

net=init(net);

net.trainParam.goal=0.001;

net.trainParam.epochs=3000;

net=train(net,P,T);

%仿真

Y=sim(net,P);

plot(P,T,'-o',P,Y,'o')

%训练误差

Z=sim(net,P);

error=Z-T;

res=norm(error);

res

2.模型的算法选择

在网络的输入层输入学生课程成绩的数据集，模型的训练样本采用50名学生10门课程成绩，训练次数设置最多为3000次，分别选用L-M优化算法、有动量的梯度下降法、可变学习速率的梯度下降法和弹性梯度下降法等进行学习训练网络，训练过程如图3所示。

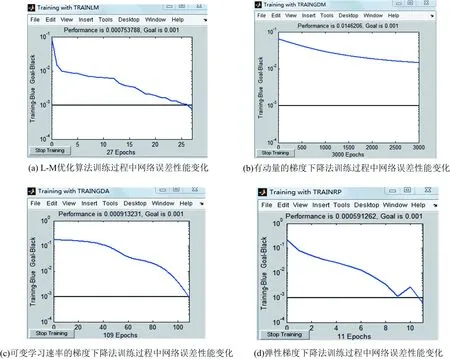
图3 人工神经网络训练过程

从网络训练过程图上的误差性能变化，我们看到有动量的梯度下降法经过3000次迭代后，依然无法实现期望的误差；可变学习速率的梯度下降法，经过109次迭代实现误差性能，收敛速度较慢；弹性梯度下降法，实现了误差期望并且收敛速度较快，但是网络出现了较大振荡变化，稳定较差；当学习训练算法选择L-M优化算法的时候，网络的预测效果最为理想，收敛速度快，实现了误差性能[7]。

4.3 学分绩点预测模型性能测试

为了测试学分绩点预测模型基本性能，在MATLAB中运用sim函数进行仿真，检测所训练网络的准确性。将样本的课程成绩输入到模型的输入层，通过模型运行，在输出层得到输出结果。将实际输出与期望输出进行比较，若两者之间的误差满足要求，说明该模型准确性较高，否则就需要对参数重新设定，并进行训练，直到误差符合要求[8]。

表3列举比较了模型的实际输出和期望输出，从两组数据对比可知，在实际输出与期望输出之间有一些差别，但误差值很小，绝对误差的平均值为0.02%，相对误差的平均值为0.37%。总体而言，两者反映的信息可以认为是相同的，因此本文认为该模型能够用于学分绩点的预测。

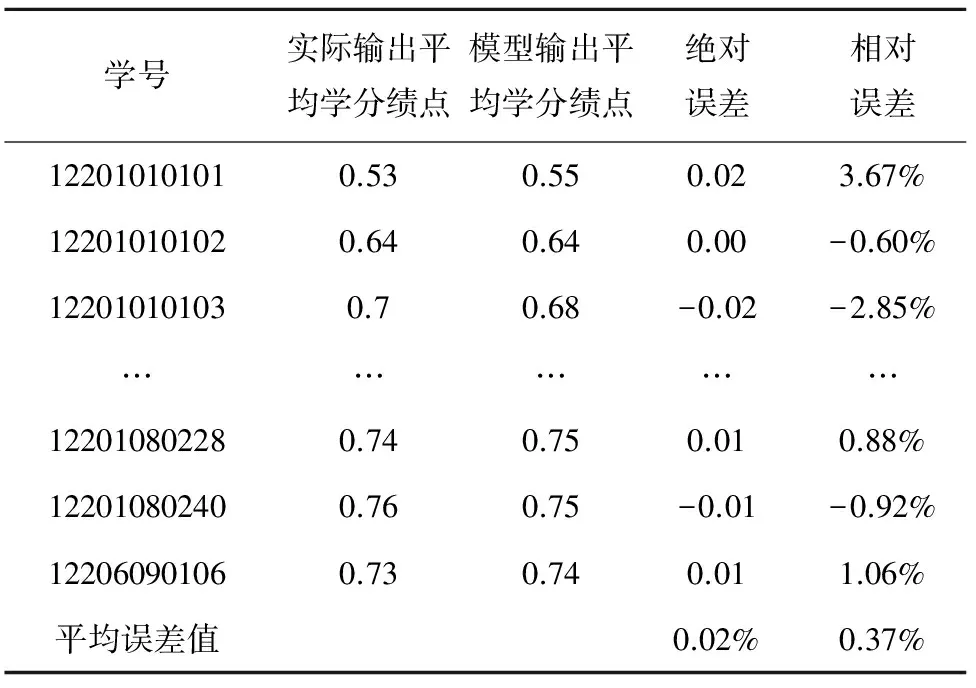
表3 测试样本的神经网络预测模型输出和实际输出值比较

5 结论

本文构建了基于BP神经网络的平均学分绩点预测模型，学生每学期获得成绩作为模型输入，学生平均学分绩点值作为模型输出。当隐层节点数为9时，模型满足了网络的实际输出与期望输出的误差要求，即该模型能够映射课程成绩与平均学分绩点之间的函数关系。最后，经过实验测试结果表明，在学分绩点预测模型构建中L-M优化算法优于其他算法，可以应用于智能学业预警，具有一定的理论和实际应用价值。

[1] 方祥玉. 学分绩点制在武汉七所部属高校的实践与探索[J]. 河南教育学院学报(哲学社会科学版). 2012：131-132.

[2] 翟雪松，尹吉明，林莉兰. 结构方程视角下我国翻转课堂满意度模型构建[J]. 高教探索，2015，(05)：65-72.

[3] 陆玉娇，赵雪花，安莉莉. 快速BP算法在年径流预测研究中的应用[J].水资源与水工程学报. 2012：96-97.

[4] 刘磊. BP神经网络在极限承载力预测中的应用[J].河南科技. 2012:01-15.

[5] 马正华，王腾，周炯如. 基于BP神经网络的太湖富营养化时空变化预测[J]. 常州大学学报(自然科学版). 2013：63-64.

[6] 王涛, 翟雪松. 基于神经网络的智能课程推荐模型[J]. 合肥学院学报(自然科学版). 2016.1：32-34.

[7] 董升伟. 基于改进BP神经网络的轨道交通短时客流预测方法研究[D]. 北京交通大学. 2013.

[8] 俞克强，宫宁生，丁磊. 一种神经网络控制模型的研究与应用[J]. 计算机应用与软件. 2013：61-62.

[9] 周志华，曹存根,主编.神经网络及其应用[M].北京：清华大学出版社, 2004.

[10] MartinT.Hagan，HowardB.Demuth，MarkH.Beale，著.神经网络设计[M].北京：机械工业出版社， 2002.