具p-Laplace算子微分方程多点边值问题正解的存在性
杨 刘
(合肥师范学院 数学与统计学院,安徽 合肥 230061)
1 引言
本文研究如下含p-Laplacian算子常微分方程多点边值问题
(φp(x′(t)))′+f(t,x(t))=0,
0 (1.1) (1.2) 正解的存在性,其中 φp(s)=|s|p-2s,p>1,(φp)-1=φq,1/p+1/q=1,1≤k≤s≤m-2,αi,βi∈(0,). 文中我们假设下述条件成立: 0<ξ1<ξ2<…<ξm-2<1. (H2)f∈C([0,1]× 具p-Laplace算子的常微分方程边值问题广泛出现在多孔介质中气体的湍流理论、非牛顿流体理论等问题中,对这一问题的研究有深刻的应用背景. 借助于非线性泛函方法,对此类问题正解与多个正解的存在性的研究取得了丰富的结果[1,2,3]. Wang youyu, Ge weigao[4]利用锥拉伸锥压缩不动点定理得到了二阶多点边值问题 (φp(u′(t)))′+a(t)f(t,u(t),u′(t)) =0,t∈(0,1) 正解的存在性结论. Xu fuyi[5]利用范数形式的锥拉伸锥定理压缩不动点定理证明了含p-Laplace算子二阶微分方程边值问题 (φp(u′(t)))′+f(t,u(t))=0,0 正解的存在性. 为了在证明过程中用到解的凹性,上述文献都假设问题的非线性项f非负.目前,关于具有变号非线性项p-Laplace算子边值问题正解的研究还比较少.本文利用双锥上不动点定理,在非线性项变号的情况下,证明边值问题(1.1,1.2)正解的存在性,推广了已有文献的结果. 设K是Banach空间X上的一个锥.设r>0是一个常数,令 Kr={x∈K:‖x‖ 设α:K→R+是非负连续的增泛函,即α是连续的且对λ∈(0,1),α(λx)≤λα(x).令 K(b)={x∈K:α(x) 引理1.1[6]设K,K′是Banach空间X上的两个锥,且K′⊂K.设T:K→K和T′:K′→K′是两个全连续算子.α:K′→R+是一个非负连续的增泛函.若存在常数b>a>0使得下列条件满足: (C1) 对x∈∂Ka,‖Tx‖ (C2) 对x∈∂Ka′,‖T′x‖ 则算子T在K中至少有两个不动点x1,x2使得 0≤‖x1‖ 引理2.1[5]设f(t,x(t))∈C([0,1]×R,R),边值问题 (φp(x′(t)))′+f(t,x(t))=0,0 有唯一解 其中 K={x∈X:x(t)≥0,t∈[0,1]},K′={x∈X:u(t)∈K,x(t)在 [0,1]上是凹的}. 显然,K,K′是X中的两个锥,且K′⊂K. 记正常数 引理2.2设非负函数x(t)满足边值条件(1.2),且满足x′′(t)<0,t∈[0,1],则有x(t)在[0,1]上单调递减且 x(t)≥γ||x(t)||,t∈[0,1], 对x∈K,定义算子 对x∈K′,定义 (T′x)(t)= 其中(B)+=max{B,0}.对x∈K,定义θ:X→K,(θx)(t)=max{x(t),0}. 定理1设条件(H1),(H2)成立,且存在常数a,b,d>0使得0 (H3)f(t,x)≥0,(t,x)∈[0,1]×[d,b]; 则边值问题 (1.1),(1.2)至少有两个正解并满足 0<‖x1‖ 证明对u∈∂Ka,由条件(H4), ||Tx||= 则T不动点x1满足0 (Ax1)(t)<0=x1(t),t∈(t1,t2). 由条件(H2),[t1,t2]≠[0,1]. 以下分两种情况: 对u∈∂K′(δb),有δb≤u(t)≤b,由条件 (H5),有 μ(T′(x))= x(t)≥‖x‖>γa>d,t∈[0,1], 0<‖x1‖ 考虑如下三点边值问题 φ1.5(x′)′+f(t,x)=0,0 (4.1) (4.2) 其中 f(t,x)= 取d=1,a=11,b=45 经计算得 f满足f(t,0)>0,t∈[0,1]且 当(t,x)∈[0,1]×[1,45]时,f(t,x)≥0; 定理1的条件均成立,边值问题(4.1),(4.2)至少存在两个对称正解且满足. 0<‖x1‖<11≤‖x2‖,μ(x2)<15. [1] R. P. Agarwal et. al,Eigenvalues and the one-dimensionalp-Laplacian[J]. J. Math. Anal. Appl. 266(2002): 383-400. [2] R. P. Agarwal, D. O′Regan,Twin solutions to singular Dirichlet problems, J. Math. Anal. Appl. 240 (1999) 433-445. [3] Z. Bai, Y. Wang, W. Ge, Triple positive solutions for a class of two-point boundary value problems, Electron. J.Differential Equations 06 (2004) 1-8. [4] Y. Wang, W. Ge, Positive solutions for multipoint boundary value problems with a one-dimensionalp-Laplacian[J]. Nonlinear Anal., 66 (2007) 1246-1256. [5] F. Xu, Positive solutions for multipoint boundary value problems with one-dimensionalp-Laplacian operator [J]}, Appl. Math. Comput., 194 (2007) 366-380. [6] 郭彦平,葛渭高,董士杰,具有变号非线性项的二阶三点边值问题的两个正解[J].应用数学学报,2004(3) 522-529.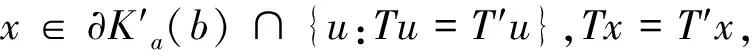
2 主要结论
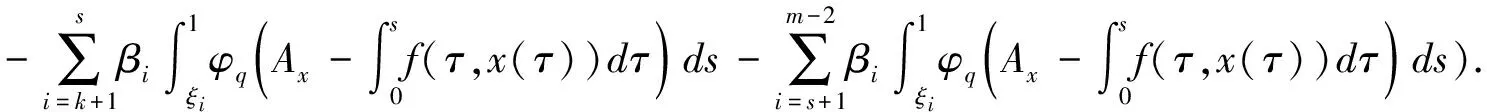
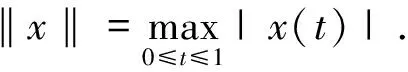
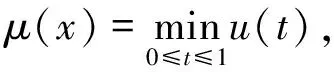
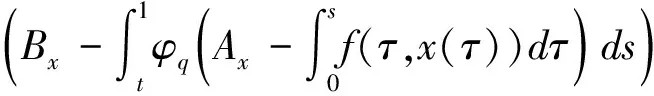
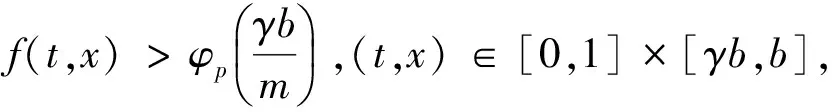




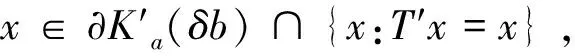
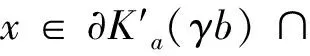
3 例子