多级微结构表面润湿性的尺度效应分析
,, ,
(浙江工业大学 特种装备制造与先进加工技术教育部重点实验室,浙江 杭州 310014)
在最近十几年中,各种微结构表面所引起的奇异润湿性引起了研究人员的广泛关注.润湿性可以定义为液滴在固体表面保持接触的能力.自然界中存在许多令人惊叹的超浸润表面的案例,例如:荷叶表面的自清洁、玫瑰花瓣表面液滴的黏附等,受此启发研究人员做了大量研究,发现其表面存在微纳米复合结构,通过各种制备方法可以人工制备出多种微纳复合结构[1-2].
对于一级微结构表面,其润湿状态分为两种:一种为Cassie模型[3](CB状态),即液滴在微结构表面.另一种为Wenzel模型[4](W状态),即液滴浸入微结构.近年来,人们发现随着表面结构尺度的减小,线张力的影响并不能忽略,开展了大量的理论、仿真和实验工作[5-9].Widom等[10]研究了线张力对小液滴接触角的影响,并预测了润湿转型行为.吕存景等[9]和Lipowsky等[11-12]研究了线张力作用下液滴在光滑和粗糙基底上的粘附问题.Iwamatsu等[7,13]研究了线张力液滴在球形结构表面润湿性的影响,并用进行了仿真验证.柴国钟等[14]也发现了纳米尺度的铁电薄膜中存在尺度效应.从以上研究工作可以发现,对于小尺度微结构表面,存在尺度效应,线张力的影响并不可以忽略.对于微纳复合结构表面,吴兵兵等[15]润湿状态将润湿状态分为4种,并分别给出了对应状态的接触角预测方程.但是没有考虑尺度效应的影响.以往的研究都是针对一级微结构展开的,缺少多级微结构表面润湿性的尺度效应方面的工作.笔者着重分析多级微结构表面润湿性的尺度效应,研究考虑线张力情况下不同尺寸的微纳结构的表观接触角以及润湿稳定性.首先通过热力学模型,推导出考虑线张力影响后液滴在4种润湿状态下的接触角方程,建立线张力和表观接触角的关系;其次分析尺度的变化对表观接触角的影响;最后分析液滴在不同尺度微纳结构表面转型所需突破的临界压力以及能量势垒.
1 热力学模型
1.1 考虑线张力后液滴表观接触角预测方程
建立的模型以柱状多级结构为例,一级结构宽、高和间距分别为a1,h1,b1.二级结构宽、高和间距分别为a2,h2,b2,如图1所示.
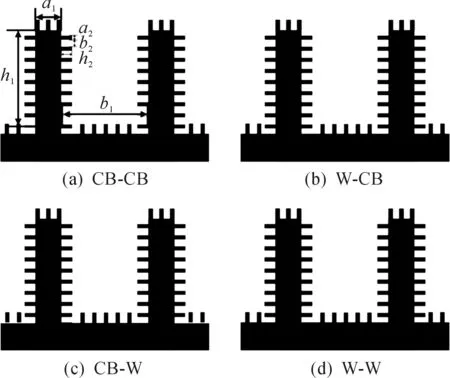
图1 柱状多级结构各润湿状态示意图Fig.1 Four wetting states on the hierarchical structures surface
线张力能量为液滴处于CB状态时,固液接触区接触线的长度乘以线张力系数.所以对于多级结构表面,当一级结构和二级结构都未被浸润,即液滴处于CB-CB状态图1(a)时,线张力能量LCB-CB可以表示为
(1)
式中:f1=a12/(a1+b1)2,f2=a22/(a2+b2)2分别为一级结构和二级结构的面积分数;A2,L2分别为二级结构的截面面积和周长;Sbase为液滴和基底的接触面积;线张力系数γ=1.57×10-8J/m[16].系统总的自由能可以表示为
(2)
式中:γLV,γSV,γSL分别为液-气、固-气和固-液界面的界面张力;SLV,SSV,SSL分别为液-气、固-气和固-液界面的面积.根据吴兵兵等[15]中的推导方法可以得出,考虑线张力影响后CB-CB状态的表观接触角预测方程为
(3)
式中θ0为基底的本征接触角.
当一级结构被浸润而二级结构未被浸润,即CB-W状态时,线张力能量LCB-W可以表示为
(4)
式中r1=1+4a1h1/(a1+b1)2为微米结构的粗糙度.此时系统总的自由能可以表示为
(5)
进一步推倒可得出考虑线张力影响后CB-W状态的表观接触角预测方程为
(6)
当一级结构不被浸润而二级结构被浸润,即W-CB状态时,线张力能量LW-CB可以表示为
(7)
式中:A1,L1分别为微米结构的截面面积和周长.此时系统总的自由能可以表示为
(8)
进一步推导可得出考虑线张力影响后W-CB状态的表观接触角预测方程为
(9)
当一级微结构和二级结构都被浸润后,三相接触线大量减少,此时线张力的影响忽略不计,W-W状态接触角预测方程[15]为
cosθW-W=r1r2cosθ0
(10)
1.2 液滴转型所需克服的临界压力以及能量势垒
在液滴转型的过程中,为了克服液滴表面张力的阻碍,外界作用的压力必须要大于液滴转型所需突破的临界压力,其表达式[17]为
(11)
当考虑线张力后,cosθadv可以表示为
(12)
当外加压力大于临界压力后,液滴的转型过程并不是马上就发生.外加压力仍需要继续作用,在克服液滴转型所需的能量势垒后转型才会完成.势垒为液滴在高能CB-CB状态态与CB-CB状态自由能的差值,无量纲化自由能表达式[18]为
(13)
当考虑线张力影响后,cosθHE其表达式为
cosθHE=f1f2cosθ0+f1(f2-1)+(f1-1)·
(14)
对于不考虑线张力的情况,令式(12,14)中线张力系数γ=0,即可得到相应的公式.
2 结果与讨论
2.1 线张力对接触角的影响
图2给出了考虑线张力情况下不同尺度微纳结构表面4种润湿状态的相图(a1/h1=a2/h2=4,θ0=110°).从图2中可以看出:CB-CB状态和W-CB状态的分界线以及CB-W和W-W的分界线在考虑线张力后都向下移动,说明由于线张力的影响会使得二级微结构更加容易被浸润.而CB-CB状态和CB-W状态区域的分界线,在考虑线张力后向右移动说明在二级微结构保持CB状态时,线张力的影响会使得一级微结构更加容易保持CB状态.W-CB状态和W-W状态的分界线在考虑线张力后却向左移动,说明在当二级微结构被浸润后,线张力的影响使得一级微结构更加容易被浸润.

图2 润湿相图Fig.2 Wetting phase diagram
取b1/a1=0.8,来分析不同二级微结构尺度时,线张力对表观接触角的影响图3(a).随着b2/a2的变化,液滴的稳定润湿状态分为4个区域.当液滴处于CB-W状态时(0
2.2 线张力对润湿转型的影响
当液滴处于CB-CB状态时,表现出好的超疏水性,因此维持CB-CB状态的稳定性显得尤为重要.由于液滴在润湿转型过程中所需要突破的临界压力随着微结构间距的减小而增大[17],一级微结构一般更加容易被浸润.因此,分析一级微结构被浸润的过程由为重要.图4给出了浸润一级微结构的润湿转型过程中,液滴所需要突破的临界压力与二级微结构面积分数的关系(f1=0.25,θadv0=113.5°).取a2=5 μm,随着f2的增加,三相接触线的长度增大,所以线张力对临界压力的影响也越来越大.而且当二级微结构尺寸减小为2.5 μm时,可以发现临界压力会进一步提升.
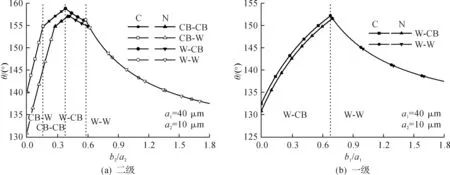
图3 考虑(C)和不考虑线(N)线张力时接触角和微结构尺寸的关系Fig.3 The relationship of apparent contact angle and microstructures relative pitch with (C) and without (N) line tension

图4 考虑线张力和不考虑线张力时润湿转型所需克服临界压力比较Fig.4 The comparison of critical pressure of CB-CB state wetting transition with and without line tension
临界压力是液滴在润湿转型过程中所需满足的必要条件.当外力超过转型所需的临界压力后,外力再继续作用满足转型过程所需的能量势垒后液滴才会发生润湿状态的转变.图5给出了CB-CB状态的无量纲化最小自由能以及高能CB-CB状态[18]考虑和不考虑线张力影响的最小自由能.高能CB-CB态的自由能和CB-CB状态自由能的差,即液滴转型需要突破的能量势垒.从图5中可以看出:当不考虑线张力影响时,能量势垒最大值在f2=0.61处.而当考虑线张力影响后,势垒随着f2的减小而增大.因为在微结构尺度不变得情况下,面积分数f2越大,三相接触线的长度越大,从而线张力的影响也变得越来越大,这与临界压力中分析的结果是相吻合的.
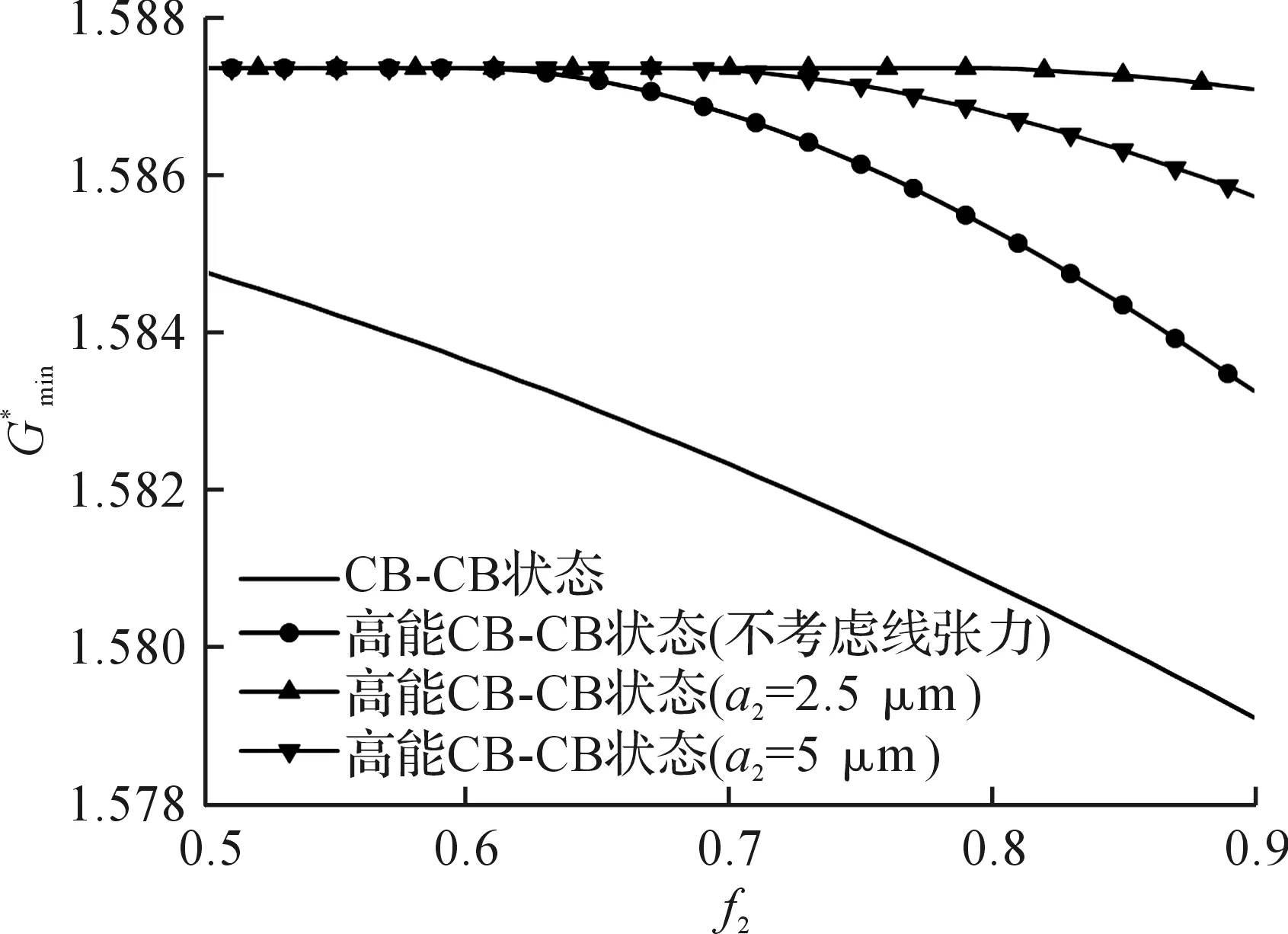
图5 考虑线张力和不考虑线张力时润湿转型能量势垒的比较Fig.5 The comparison of energy barrier of CB-CB state wetting transition with and without line tension
3 结 论
通过热力学理论,建立了考虑线张力影响后的液滴表观接触角预测模型,推导出液滴在4种润湿状态下的接触角预测公式.通过润湿相图分析,发现二级微结构在不同润湿状态时,线张力对一级微结构润湿状态的影响相反.进而具体研究了不同微结构尺度下液滴对表观接触角的影响,发现在液滴处于CB-W状态时,线张力的影响最大.由于CB-CB状态具有良好的疏水性,转型所需突破的临界压力和能量势垒也十分重要.通过分析发现在减小微结构的尺寸能提高转型所需的临界压力和能量势垒,有助于提高润湿稳定性;在微米尺度下,随着面积分数的减小,三相接触线长度增加,更有利于提高临界压力和能量势垒,提高CB-CB状态的稳定性.
[1] 肖帆,柳星竹,江光强,等.钛表面原位自组装TiO2空心球及生物活性研究[J].浙江工业大学学报,2016,44(5):580-583.
[2] 肖帆,倪爱珍,柳星竹,等.钛基体表面纳米二氧化钛薄膜生长及控制[J].浙江工业大学学报,2015,43(3):307-310.
[3] CASSIE A B D, BAXTER S. Wettability of porous surfaces[J]. Transactions of the faraday society,1944,40:546-551.
[4] WENZEL R N. Resistance of solid surfaces to wetting by water[J]. Industrial & engineering chemistry,1936,28(8):988-994.
[5] SINGHA S K, DAS P K, MAITI B. Thermostability analysis of line-tension-associated nucleation at a gas-liquid interface[J]. Physical review E,2017,95(1):012802.
[6] RASPAL V, AWITOR K O, MASSARD C, et al. Nanoporous surface wetting behavior: the line tension influence[J]. Langmuir,2012,28(30):11064-11071.
[7] IWAMATSU M. Line tension and morphology of a sessile droplet on a spherical substrate[J]. Physical review E,2016,93(5):052804.
[8] 崔树稳,朱如曾,闫红.关于线张力对液滴-固体接触角的影响问题[J].应用基础与工程科学学报,2009,17(4):622-627.
[9] 吕存景,殷雅俊,郑泉水.线张力作用下微纳米尺度液滴的非线性粘附[J].应用数学和力学,2008,29(10):1135-1146.
[10] WIDOM B. Line tension and the shape of a sessile drop[J]. Journal of physical chemistry,1995,99(9):2803-2806.
[11] LIPOWSKY R, LENZ P, SWAIN P S. Wetting and dewetting of structured and imprinted surfaces[J]. Colloids and surfaces A: physicochemical and engineering aspects,2000,161(1):3-22.
[12] SWAIN P S, LIPOWSKY R. Contact angles on heterogeneous surfaces: a new look at cassie’s and wenzel’s laws[J]. Langmuir,1998,14(23):6772-6780.
[13] IWAMATSU M. Size-dependent contact angle and the wetting and drying transition of a droplet adsorbed onto a spherical substrate: line-tension effect[J]. Physical review E,2016,94(4):042803.
[14] 柴国钟,周挺,吴化平,等.挠曲电效应对超薄铁电薄膜物理性能的调控[J].浙江工业大学学报,2015,43(2):159-162.
[15] 吴兵兵,吴化平,张征,等.微纳复合结构表面稳定润湿状态及转型过程的热力学分析[J].物理学报,2015,64(7):281-292.
[16] ZHENG Q S, LV C J, HAO P F, et al. Small is beautiful, and dry[J]. Science china physics, mechanics and astronomy,2010,53(12):2245-2259.
[17] ZHENG Q S, YU Y, ZHAO Z H. Effects of hydraulic pressure on the stability and transition of wetting modes of superhydrophobic surfaces[J]. Langmuir,2005,21(26):12207-12212.
[18] WU H P, ZHU K, WU B B, et al. Influence of structured sidewalls on the wetting states and superhydrophobic stability of surfaces with dual-scale roughness[J]. Applied surface science,2016,382:111-120.

