具有公共自行车共享系统的公交网络建模及其性能研究
,
(浙江工业大学 计算机科学与技术学院,浙江 杭州 310023)
作为一种低价、健康和环保的出行方式,公共自行车共享系统的数量增长迅速.迄今为止,全世界已经有超过数百个城市建立了公共自行车共享系统[1].公共自行车共享系统使用方式灵活,通常使用者可以从任意一个自助停靠点借出自行车,使用后在任意自助停靠点归还,从而成为传统城市公交模式(比如说:公交巴士和地铁)的一种补充方式.目前,研究新建立的公共自行车共享系统的性能及其优化方法引起了学者们的关注,并已经成为学术界的研究热点.比如说:Chardon等[2]利用公共自行车站点使用量的统计数据来评估公共自行车每天的利用情况,Gosse等[3]利用稀疏数据对在时间和空间上公共自行车网络的使用情况进行性能评估;Winters等[4]利用统计方法提出了一种可以找到适合骑行环境区域的方法,Frade等[5]提出了一种最大覆盖位置的自行车站点配置算法,Chen等[6]对公共自行车系统的站点提出了布局定位以及优化的方法.公共自行车共享系统一般都嵌入到已有的城市公交网络所处的空间中,和城市公交网络共同组成新的城市公交网络,该网络是一种空间网络,空间网络[7]是一种具有空间属性的复杂网络,该网络嵌入在所处的空间中,每个节点和边都有自己的空间(地理)位置,这种空间位置的约束对网络的属性有着重要的影响.在真实世界中,许多和地理位置相关的网络属于空间网络,如Internet[8-9]、电力网络[10-11]、航空网络[12]和道路网络[13-16]等.城市公交网络由于站点和线路都具有空间位置,因此属于典型的空间网络.此外,新公交网络往往由公共自行车共享系统、巴士子网和地铁子网组成,这些子网之间存在明显的相互影响和相互作用,而不是相互独立,属于典型的耦合空间网络[17-18].
针对目前的研究现状,提出了一个新的多层耦合空间网络模型表示整体公交系统,该网络模型中公交车和自行车站点具有地理空间位置,连边加权有向(权值为站点之间的道路长度),网络由自行车子网,步行子网和公交子网组成.在杭州和宁波实际公交网络数据的基础上,我们研究了具有公共自行车共享系统的城市公交网络的运行特点,发现短距离自行车骑行和短距离步行可以显著地改善城市公交网络性能.
1 城市公交系统的3层耦合空间网络模型
公交网络由站点和线路组成.常用的2种传统公交网络模型分别为Space L和Space P[19].在2种模型中,节点都表示公交站点,所不同的是边的表达方式.在Space L中,2个站点如果是一条公交线路上的相邻站点,则这2个站点就有连边;在Space P中,2个站点如果同时位于一条公交线路,则这2个站点就有连边.Space L反映公交网络的完整的空间拓扑结构,Space P网络则用来研究公交网络的换乘.如图1(a)所示,图中有3条公交线线路,其中不同的虚线表示不同的公交线路,箭头表示公交车的行驶方向,箭头上的数值表示权值,即公交线路的长度(单位为km).
为了表达公交网络的空间特性,我们对Space L和Space P网络进行了扩展,使之可以表示网络的空间位置因素,称之为空间Space L和Space P网络,如图1所示,这2种网络为具有空间信息的加权有向网络,其新的特性为:表示公交站点的节点具有空间位置信息(经纬度)、2点之间的边反映公交线路的方向,其权值为2点之间公交线路的实际长度.如图1(b)所示的是空间Space L网络模型,图1(c)所示的是空间Space P网络模型.

图1 公交网络模型示意图Fig.1 Public transport network models
为研究短距离步行对公交网络性能的影响,我们提出了短距离空间步行网络,为无向加权的空间网络.在短距离空间步行网络中,节点为具有空间位置信息的公交站点,任意2个欧式距离小于阈值Tw(短距离步行的最大值,比如500 m)的站点(这2个站点被称之为短距离步行站点对)之间有连边,连边的权值为2点之间的欧氏距离.我们把短距离步行站点对之间的步行简称为短距离步行.
近年来对人们使用公共自行车共享系统行为特性的研究表明,绝大多数自行车出行都是短距离短时间的[13].我们提出了短距离空间自行车网络,为无向加权的空间网络,在短距离空间自行车网络中,节点为具有空间位置信息的公共自行车公交站点,任意2个欧式距离小于阈值Tb(短距离自行车骑行的最大值,比如2 000 m)的站点(这2个站点被称之为短距离自行车站点对)之间有连边,连边的权值为2点之间的最短道路路径长度.我们把短距离自行车站点对之间的骑行简称为短距离自行车骑行.
由于只关注位于公交站点附近的公共自行车站点,如图3所示,为简化模型的复杂性,我们把某一公交站点附近300 m之内的所有公共自行车站点的位置,都合并为该公交站点.公交站点S1附近的自行车站点B1,B2,B3,其地理位置都被认定为S1的位置;公交站点S2附近的自行车站点B4,B5,B6,其地理位置都被认定为S2的位置;则S1和S2附近的自行车站点距离均为S1和S2之间的最短道路路径长度.
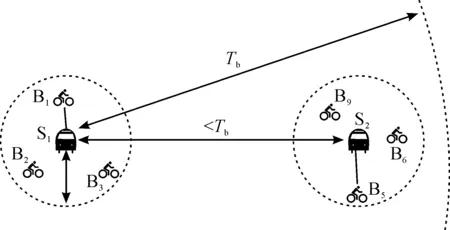
S1,S2—公交站点;B1,B2,B3—公交站点S1附近的自行车站点;B4,B5,B6—公交站点S2附近的自行车站点;Tb—短距离骑行阈值图2 短距离空间自行车网络构建具体实例图Fig.2 Principle of creating short-distance spatial bicycle network model
我们可以认为整体公交系统是由公交网络、短距离空间自行车骑行网络和短距离步行网络3个网络层组成,3层网络节点都为公交站点,其中短距离自行车骑行和短距离步行的节点是城市公交网络的节点一部分,任意2个网络层之间通过公共节点(公交站点)可以自由地换乘(节点之间可以通过公交、步行以及骑行3种不同的方式进行换乘),也就是说3个网络层是通过共享的公交站点耦合在一起的,3层网络相互依赖并相互影响,从而构成公交系统3层耦合网络.
2 换乘性能影响分析
基于中国杭州和宁波的2016年的公交系统[20]的真实数据,应用公交系统的3层耦合空间网络模型研究短距离自行车骑行和短距离步行对城市公交网络性能的影响,杭州和宁波公交系统的基本数据在表1中列出,公交线路和自行车站点的分布如图3所示,其中线表示公交线路,点表示公共自行车站点.
表12个城市公交车与公共自行车基本数据信息
Table1Basicdatainformationonthebusandbicyclestationsoftwocities

城市S1)/个R2)/个SD3)/kmBS4)/个杭州29438900.6343866宁波32616270.3952493
注:1) 公交车站点数目;2) 公交路线数量;3) 公交站点间的平均道路长度;4) 自行车站点数目.

图3 2个城市的站点分布图Fig.3 Distribution of bus routes and bicycle stations of two cities
为了分析新网络模型对城市公交网络模型的影响,Tb和Tw的取值不同将形成不同规模的短距离自行车骑行和短距离步行,从而对城市公交网络的性能产生不同的影响.公交网络中,任意2点i和j之间的换乘次数为公交线路的最短路径减1,表示从i到j需要换乘公交车的数量,而网络的平均路径长度是公交网络性能的重要指标,平均路径长度越低表示城市公交网络的性能越好,反之则越差.
在图4中,根据杭州和宁波公交系统中公交站点、公交线路和自行车站点的空间地理位置信息,我们给出了Tb,Tw和公交网络平均路径长度的三维关系图.其中,x坐标表示自行车阈值Tb变化,y坐标表示步行阈值Tw变化,z坐标表示公交网络的平均路径长度.当骑行阈值和步行阈值都为0时,其平均路径长度最高,随着Tb和Tw的逐渐增长,2个城市公交网络的平均路程长度都呈现了递减的趋势,其中,Tb和Tw数值较小时,平均路径长度有急剧的下降;Tb和Tw数值较大时,平均路径长度下降的幅度较小;这表明Tb和Tw有一组可行值,并不是越大越好,这也比较符合人们的出行习惯,人们一般在短距离内而不是长距离地使用自行车和步行作为出行手段.结合实际出行经验以及图4给出的趋势图,把Tb和Tw的主要可行值确定为Tw=0.5 km,Tb=2.2 km.

图4 平均路径长度(ANR)趋势3D图Fig.4 Three-dimensional relationship diagram of the average number of bus routes
3 在可行阈值下的公交性能分析
在上节中得到了主要可行短距离骑行阈值Tb=2.2 km和步行阈值Tw=0.5 km,将在2个主要可行阈值的情况下,对公交网路的属性和性能进行分析,研究短距离自行车骑行和短距离步行对城市公交网络的影响.
3.1 度分布
网络中每个节点所连接的边的数目就是这个节点的度,而对于每个节点所组成的度分布是评估网络性能的比较重要的指标,它描述网络中度的所组成的分布的序列,是对整体网络节点度的全部格局的描绘.我们分别描述了空间Space L网络、空间Space P网络、短距离空间自行车网络与短距离空间步行网络的度分布序列.为消除数据的噪声误差,对空间Space L网络、空间Space P网络、短距离空间自行车网络使用累积度分布Pk来表示.而空间Space L网络和空间Space P网络的度的范围相对比较大,为了拟合更加清晰,采用了半对数坐标来表示这2个网络的度分布.由于短距离空间自行车网络和短距离空间步行网络的度的范围不是很大,使用基本的累积度分布来表示短距离空间自行车网络,短距离空间步行网络则采用普通度分布表示.具体度分布表示如图5所示,其中横坐标k表示度分布为k的情况,纵坐标P(k)表示度数为k的分布概率,实心点表示杭州,叉点表示宁波.
从图5中可以看出:对于空间Space L网络与空间Space P网络,其累积度分布的半对数坐标呈指数分布(p(x)~e-αx).这表明公交网络是随机连接生成的增长网络[21].对于短距离空间自行车网络,其累积度分布则呈现均匀分布的特性(p(x)~kx+b).短距离空间步行网络的度分布则近似趋近于高斯分布(p(x)~e-((x-μ)/σ)2).这表明短距离空间自行车网络和短距离空间步行网络是随机网络,其度分布是随机分布,没有偏好性.
3.2 边长分布
公交网络模型中边的长度指的是2个站点间实际路径的距离,边的长度对计算公交出行代价和换乘方案等具有重要的作用,图6给出了空间Space L网络、空间Space P网络、短距离空间自行车网络和短距离空间步行网络模型的边长分布示意图,其中使用累积边长分布来表示空间Space L网络、空间Space P网络,而短距离空间自行车网络和短距离空间步行网络用普通的边长分布来表示.图中杭州为实心点以及实线拟合线,宁波为叉点和虚线拟合线.横坐标x表示网络中的边长(单位为km),纵坐标P(x)表示边长为x的分布概率.
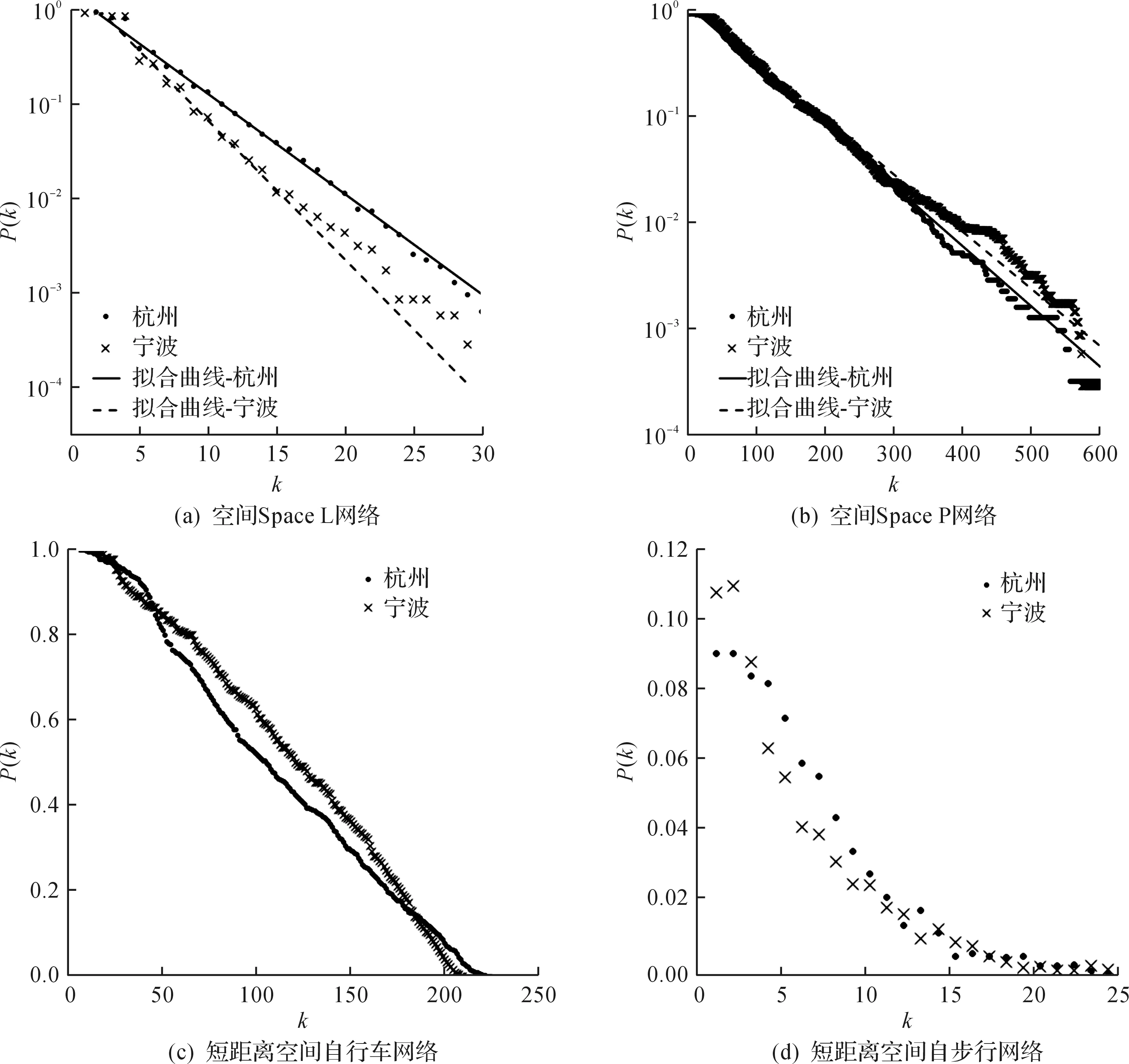
图5 网络模型的度分布图Fig.5 Degree distributions of networks

图6 网络模型的边长度分布图Fig.6 Edge length distributions of networks
根据图6可知:用边长累积分布表示的空间Space L网络近似服从幂律分布p(x)~x-β,表明人们在设置2个相邻公交站点之间距离时,是有偏好的,绝大多数站点间的间距比较短,而只有极少数的站点对之间有较大间距;空间Space P网络的边长累积分布近似服从指数分布p(x)~e-αx,表示人们在设置公交线路的总长度时,是根据随机需求的随机设置,没有明显的偏好性.另外,短距离空间自行车网络和短距离空间步行网络的边长分布则呈现了类似的线性分布p(x)~γx,这说明了自行车和步行网络有相似的边长特性,即网络边长和网络规模成正比,网络规模越大,出现大的边长的概率也越高.
3.3 公交网络换乘性能
公交网络平均路径长度是表示网络换乘性能的重要指标,借助3层空间耦合网络的公交换乘算法,我们计算了2个城市网络的平均路径长度,如表2所示,在此公交换乘算法中,由于步行和骑公共自行车的代价很小,因此不考虑其换乘次数.
表2公交网络的平均路径长度统计数据1)
Table2Statisticaldataontheaveragepathlegthofpublictransportnetwork

城市ANR1ANR2ANR1/ANR2杭州3.201.880.58宁波3.142.060.66
注:1) ANR1,ANR2分别为只考虑公交车、加入公共自行车的公交网络平均路径长度.
从表2中可以看出:短距离自行车骑行和短距离步行使公交网络平均路径长度有大幅下降,杭州下降至原来的58%,宁波下降至原来的66%,可以看出换乘性能有了很大的改善.
4 结 论
借助考虑公交车站点、自行车站点和公交线路的空间地理位置信息的多层耦合空间网络模型,公共自行车对城市公交系统性能的影响得以表现,特别主要集中在短距离自行车骑行和短距离步行对城市公交系统的影响方面.结果表明:短距离自行车骑行和短距离步行可以有效降低乘客出行的换乘次数,减少乘客出行的时间,从而可以提升城市公交系统的运行效率.研究如何部署公共自行车中自行车站点的最优数量和最优位置,如何以最小代价的公共自行车实现在城市公交系统的最优性能将是未来的研究课题.
[1] RUSSELL M. The bike-sharing world map[EB/OL]. [2016-10-02]. http://www.bikesharingworld.com.
[2] CHARDON C M D, CARUSO G. Estimating bike-share trips using station level data[J]. Transportation research part B methodological,2015,78:260-279.
[3] GOSSE C, CLARENS A. Estimating spatially and temporally continuous bicycle volumes by using sparse data[J]. Transportation research record: journal of the transportation research board,2014(2443):115-122.
[4] WINTERS M, BRAUER M, SETTON E M, et al. Mapping bikeability: a spatial tool to support sustainable travel[J]. Environment and planning B: planning and design,2013,40(5):865-883.
[5] FRADE I, RIBEIRO A. Bike-sharing stations: a maximal covering location approach[J]. Transportation research part A: policy and practice,2015,82:216-227.
[6] CHEN J, CHEN X, JIANG H, et al. Determining the optimal layout design for public bicycle system within the attractive scope of a metro station[J]. Mathematical problems in engineering,2015(2134):1-8.
[7] BARTHÉLEMY M. Spatial networks[J]. Physics reports,2011,499(1):1-101.
[8] PASTORSATORRAS R, VZQUEZ A, VESPIGNANI A. Dynamical and correlation properties of the internet[J]. Physical review letters,2001,87(25):258701.
[10] AMARAL L A N, SCALA A, BARTHELEMY M, et al. Classes of small-world networks[J]. Proceedings of the national academy of sciences of the united states of America,2000,97(21):11149-11152.
[11] ALBERT R, ALBERT I, NAKARADO G L. Structural vulnerability of the North American power grid[J]. Physical review e statistical nonlinear & soft matter physics,2004,69(2):292-313.
[12] WUELLNER D R, ROY S, D’SOUZA R M. Structure and resilience of networks: airlines in USA[J]. Physical review E,2009,82(5):514-539.
[13] AUSTWICK M Z, O’BRIEN O, STRANO E, et al. The structure of spatial networks and communities in bicycle sharing systems[J]. Public library of science,2013,8(9):e74685.
[14] LEVINSON D, YERRA B. Self organization of surface transportation networks[J]. Transportation science,2006,40(2):179-188.
[15] 杨旭华,李传告,陈光.基于K-最短路径的交通网络传输性能分析[J].浙江工业大学学报,2014,42(3):249-252.
[16] 杨旭华,汪向飞.基于低采样率浮动车数据的全局投票地图匹配算法[J].浙江工业大学学报,2015,43(3):318-325.
[17] YANG X H, CHEN G, CHEN S Y, et al. Study on some bus transport networks in China with considering spatial characteristics[J]. Transportation research part A: policy and practice,2014,69:1-10.
[18] MORRIS R G, BARTHELEMY M. Transport on coupled spatial networks[J]. Physical review letters,2012,109(12):128703.
[19] SEN P, DASGUPTA S, CHATTERJEE A, et al. Small-world properties of the Indian railway network[J]. Physical review E,2003,67(3):036106.
[20] 高德软件.高德地图[EB/OL].[2016-12-20].www.amap.com.

