影响IEEE 1588时钟同步精度的关键因素
赵 勇, 高彦杰
(上海电力学院 电子与信息工程学院, 上海 200090)
随着电力自动化系统的发展和分布式网络的广泛应用,对于系统的时间同步精度要求越来越高.比如在线路行波故障测距中要求时间同步误差小于1 us.IEEE 1588是关于网络测量和控制系统的精确时间协议[1],可实现高精度的时间同步.IEEE 1588 协议规定了主从时钟通过周期性地交换带有时间戳的报文,根据这些报文,从时钟计算出其与主时钟的时间和频率偏差,通过对从时钟自身进行调整,以达到时钟同步的目的.目前对IEEE 1588时间同步精度的研究大都以硬件开发平台为主[2],关于IEEE 1588时间同步的软件仿真平台相对较少,并且一般都是针对IEEE 1588协议某一个方面的研究.例如张城等人[3]提出了一种IEEE 1588时钟同步仿真模型,其中的主从时钟都是用关于时间的一次函数来代替,其主要目的是研究PI参数优化对同步精度的影响;ZDENEK Chaloupka等人[4]提出了一种基于时钟的IEEE 1588协议仿真模型,它仅局限于协议中报文时间戳产生部分.文献[5]提出了一种较为完整的IEEE 1588时钟同步软件仿真系统.本文将利用这个经过校验的仿真平台完成对IEEE 1588时间同步效果的仿真实验并进行仿真分析,得到主从时钟晶振精度、同步周期等因素对IEEE 1588同步系统的时间同步效果的影响,由此提出在实际应用中可以用来提高同步精度的措施.
1 时钟同步系统仿真模型
IEEE 1588时钟同步系统模型如图1所示.从功能上可将其分为3个模块,即:晶振模块;协议模块;从时钟伺服控制模块.晶振模块产生标准晶振频率和晶振噪声,然后输入到协议模块进行相应的处理后产生主从时钟时间戳,从时钟伺服控制模块得到主从时钟时间戳后,进行主从时钟同步运算,得到从时钟误差调整量,再对从时钟进行调整,以完成主从时钟同步.

图1 IEEE 1588时钟同步系统
1.1 晶振模块
现有IEEE 1588协议研究中的晶振模型一般简化为高斯噪声模型[6].为了更加贴合实际情况,本文采用了公认的幂率谱晶振模型[7].对于一个晶振频率源,设标称频率为f0,瞬时频率为f,定义瞬时相对频率偏差(晶振噪声)为y(t),则
在幂率谱晶振模型中,y(t)的功率谱密度可表示为:
Sy(f)=h-2f-2+h-1f-1+
h0+h1f+h2f2
(1)
由式(1)可以看出,晶振噪声由5种噪声组成:h-2项为随机游走调频噪声;h-1项为闪变调频噪声;h0项为白色调频噪声;h1项为闪变调相噪声;h2项为白色调相噪声.在晶振仿真中可以用高斯白噪声通过不同的整形滤波器得到上述5种晶振噪声.其幂律谱系数分别为:h-2=1.24e-17,h-1=5.925e-16,h0=3.216e-15,h1=6.85e-16,h2=2.18e-17[8].
1.2 协议模块
IEEE 1588协议的消息传递过程如图2所示.需要注意的是,该模块有3个时间参考,分别为主时钟晶振频率、从时钟晶振频率和理想时钟频率.
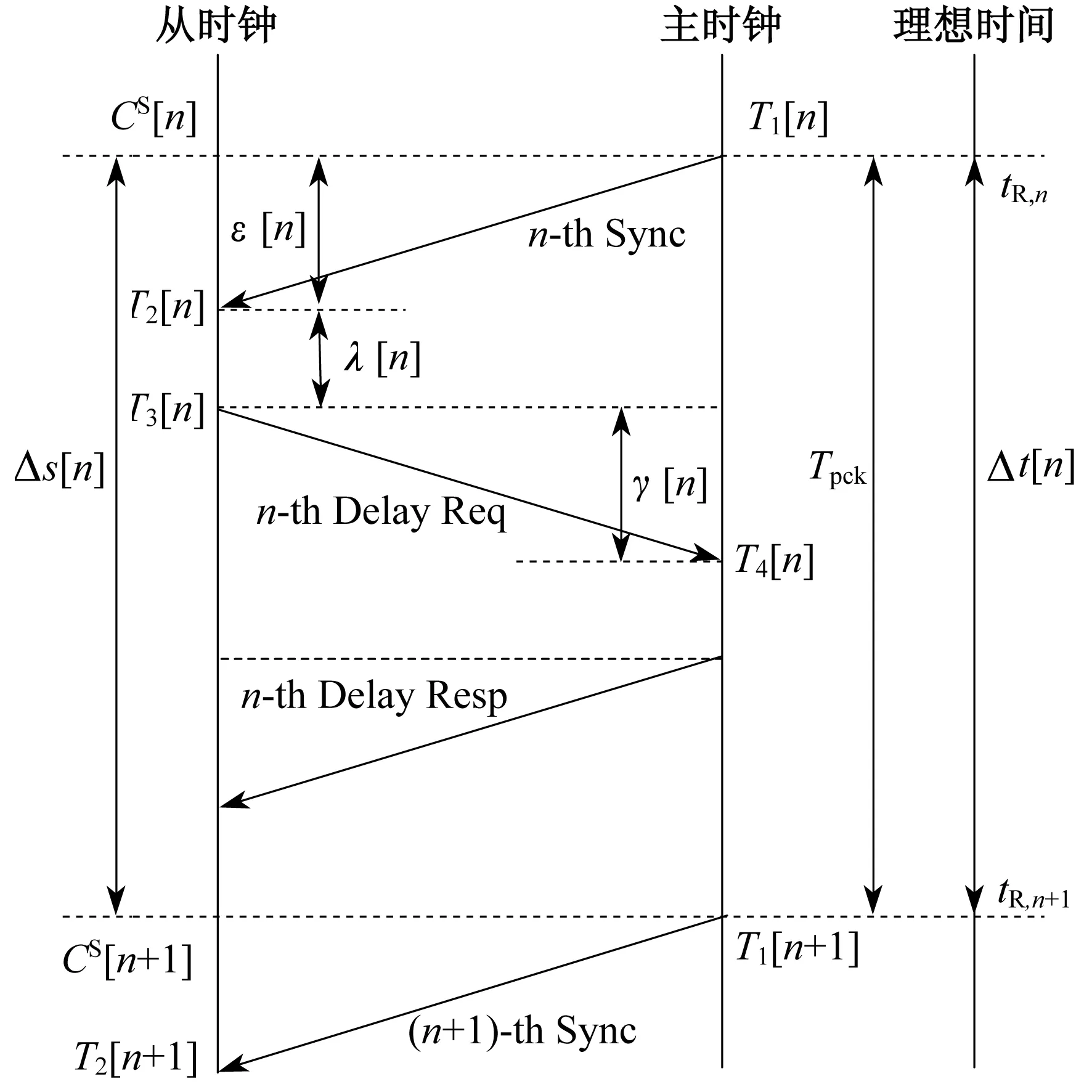
图2 IEEE 1588协议从时钟、主时钟和
图2中,主时钟以Tpck为周期发送同步报文,Tpck是以主时钟频率(fM)为参考的量,相对应,以时钟频率(fS)为参考时间的量为Δs[n],以理想频率(fR)为参考时间的量为Δt[n].它们之间的关系为:
(2)
图2中,主时钟发送SYNC报文时间戳为T1[n],相应的,从时钟计数器时间为CS[n],从时钟接收SYNC报文时间戳为T2[n],从时钟发送DELAY_REQ报文时间戳为T3[n],主时钟接收DELAY_REQ报文时间戳为T4[n].根据IEEE 1588协议,它们可分别表示为:
式中:εS[n]——从时钟测量的正向延迟,表示报文由主时钟发送至从时钟所需要的时间;
λS[n]——从时钟测量的处理延迟,表示从时钟接收SYNC报文到发送DELAY_DEQ报文所需要的时间;
γM[n]——主时钟测量的反向延迟,表示DELAY_DEQ报文从从时钟发送到主时钟所需要的时间,并且在T4[n]中需要将正向延迟和处理延迟变换成主时钟时间.
正向延迟、处理延迟和反向延迟的理想时间量与相应主从时间量之间的换算公式为:
(5)
式中:νM,S[n]——经换算得到的相应主从时间量;
ψ[n]——正向、反向和处理延迟的理想时间量.
通过上面的分析得到IEEE 1588协议主时钟和从时钟simulink仿真模型如图3所示.
1.3 从时钟伺服控制模块
从时钟伺服控制系统[9-10]如图1虚线部分所示.它首先对协议模块中得到的4个时间戳(T1,T2,T3,T4)进行如下计算.由主(从)时钟发送(接受)SYNC报文时间戳得到主从时钟延迟(dm2s):dm2s=T1-T2;由从(主)时钟发送(接受)DELAY_DEQ报文时间得到从主时钟延迟(ds2m):ds2m=T3-T4.计算中假设传播延迟是对称的,这样就产生了消息传播延迟(dprop)及从时钟偏移量(doffset):
(6)
从时钟偏移量doffset通过零阶保持器和PI控制器两个模块后产生从时钟的矫正量,再对从时钟进行调整,使其达到与主时钟同步.

图3 主时钟和从时钟simulink仿真模型
2 IEEE 1588仿真实验分析
2.1 晶振准确度对同步精度的影响
在IEEE 1588时间同步系统中,主从时钟的时钟频率由晶振产生,而对于不同的晶振有着不同的频率准确度.表1是常见频率标准的准确度.
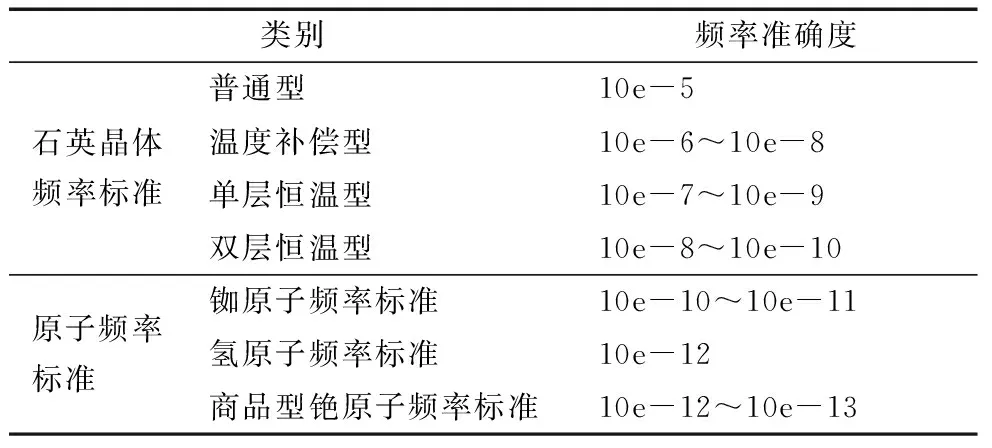
表1 常见频率标准的准确度
晶振的准确度是分析IEEE 1588时间同步必须考虑的因素.本仿真将主从时钟晶振的准确度范围为0~2.0×10-4,主从时钟标准频率均是50 MHz,同步周期为125 ms.为了简化,将正向、反向和处理延迟时间均设定为常数,分别为:20e-6 s,1e-6 s,25e-6 s.仿真得到不同准确度的主从时钟晶振的时钟同步精度三维图如图4所示.

图4 主从时钟晶振准确度变化
图4中,当主(从)时钟准确度固定,从(主)时钟由0到2.0×10-4变化时,时钟同步精度值不断变大,由此得到主从时钟的晶振准确度越高,相应的时钟同步系统的收敛精度也越高.因此,在实际应用中可以尽量提高主从时钟的晶振精度.因准确度越高成本也越高,故在实际应用中要根据不同的应用环境选择不同的晶振.
2.2 同步周期对同步精度的影响
在IEEE 1588协议中,主时钟周期性地向从时钟发送同步报文,并通过报文交换,得到完成时钟同步的数据.这个发送同步报文的周期也就是主从时钟的同步周期.同步周期是可以人为设定和调控的.本文通过对同步周期的调整来研究同步精度的变化情况.其中,同步周期为0.05~2 s变化,主从时钟均是50 MHz,±5.0×10-5晶振,为了简化,将正向、反向和处理延迟时间均设定为常数,分别为20e-6 s,1e-6 s,25e-6 s.最终得到的仿真结果如图5所示.

图5 同步周期变化对同步精度的影响
图5中,当时钟同步周期从0.05~2 s变化时,收敛精度值增大,并且时钟同步周期在0.05~1.6 s期间,收敛精度以较小增幅增长;当时钟同步周期在1.6~2 s期间,收敛精度突然成指数式增长.由此可知,同步周期越长,整个时钟同步系统的收敛效果越差,且在某一个同步时间会发生指数式的变化.因此,在实际应用中我们要控制同步周期在一个合理的范围内,尽量控制同步周期在一个较小的值内.
3 结 语
本文引用了一个相对完整并且经过验证的IEEE 1588时钟同步仿真平台,该平台采用了公认的晶振模型.以此平台为基础,研究分析了主从时钟晶振的晶振准确度变化对同步精度效果的影响,结果表明,主时钟或从时钟的晶振漂移对同步精度误差产生的影响程度相同,主时钟(或从时钟)晶振漂移参数变化与同步精度误差变化关系近似为线性,其变化率约为4.0×10-5.此外,同步周期时间对同步精度误差影响可分为两个部分,当同步周期小于1.6 s时,对精度误差影响相对较小;而当同步周期大于1.8 s时,同步精度误差随同步时间增加,呈现急剧上升的趋势.下一步的工作主要是对时钟伺服控制模块中的PI控制器的参数优化,以及运用滤波器等手段对时钟伺服控制模块进行优化和改进.
[1] EIDSON J,KANG L.1588—2008—IEEE standard for a precision clock synchronization protocol for networked measurement and control systems[J].Imprimerie Nouvelle,V.Berthod,2008(2):98-105.
[2] 黄健,刘鹏,杨瑞民.IEEE 1588 精确时钟同步协议从时钟设计[J].电子技术应用,2010,36(7):91-97.
[3] 张城,陈隆道,文昊翔.基于IEEE 1588 协议的从时钟同步控制算法研究[J].工业控制计算机,2012,25(12):83-85.
[4] ZDENEK Chaloupka,NAYEF Alsindi,JAMES Aweya.Efficient and precise simulation model of synchronization clocks in packet networks[J].IEEE CAMAD,2013,39(10A):79-83.
[5] 赵勇,高彦杰.Investigations on simulation platform for IEEE 1588 precision time synchronization[C]//CST,2016.
[6] FONTANELLI D,MACII D,WOLFROM P,etal.A clock state estimator for PTP time synchronization in harsh environmental conditions[C]//IEEE ISPCS,2011:99-104.
[7] YUAN Lisong,CHEN Xiaolong,WANG Jiali.A practical simulation method for generating phase noise of oscillators[J].ICMIC,2013(1):132-136.
[8] 尚红娟.时间频率同步的优化控制方法研究[D].西安:西安科技大学,2010.
[9] 林永君,李境达,李通,等.基于IEEE 1588 协议的从时钟设计及其控制研究[J].电力科学与工程,2014,30(9):53-58.
[10] 刘见,靳绍平,李敏,等.基于IEEE 1588协议的高精度时钟对时设计[J].电子技术应用,2014,40(4):48-51.

