基于邻域熵与蚁群优化的基因选择算法
许 明,郑鹭斌,谢彦麒,陈玉明
(厦门理工学院计算机与信息工程学院,福建 厦门 361024)
0 引言
随着基因微阵列技术的提高,基因表达数据快速增长,基因数据分析与处理技术已引起学者的广泛关注[1-3]. 然而,基因表达数据集呈现高维、小样本和不确定性的特点,已经成为基因分析与处理技术的发展瓶颈,如何从高维基因数据中选取有效且区分度高的少量基因,是基于基因表达数据进行癌症肿瘤分类的科学问题之一. 通过基因选择,剔除与肿瘤分类无关的冗余基因,获得精简的基因子集,不仅降低分类器设计的计算复杂度,还可以提高分类器的分类精度.
基因选择也称特征基因子集选择,是指从全部基因中选取一个特征基因子集,使构造出来的分类模型更优[4]. 依据评价函数的不同,常见的基因选择算法主要包括Filter方法和Wrapper方法两大类[5]. 其中Filter方法依据度量评价函数,筛选出高区分度的特征基因. 其算法运行速度较快,在不同分类算法之间的推广能力较强,但评估函数与学习算法的性能偏差较大. 筛选评估函数主要有相关系数[6]、距离度量[7]、信息熵度量[8]等. 而Wrapper方法的特点是采用具体的分类算法,选取分类精度最大的特征基因[9]. 该方法分类准确率较高,选择的基因子集规模较小,但计算复杂度高,不利于大数据集,而且存在过拟合的现象.
依据搜索策略的不同,基因选择算法主要分为完全搜索、启发式搜索和随机搜索. 完全搜索策略不具备可行性,只适应于非常小的数据集. 因此,大部分算法采用启发式的搜索策略. 启发式的方法搜索速度快,适用于高维大数据集,却易陷入局部解. 随机搜索方法主要包括模拟退火[10]、遗传算法[1]、蚁群优化算法[11]等. 蚁群算法[12]是在20世纪90年代初,由意大利学者Dorigo提出的一种群智能算法. 它具有分布性、正反馈、健壮性及全局寻优等特点[13-15]. 波兰数学家Pawlak[16]提出了粗糙集理论,能够处理不一致、不精确、不确定数据. 粗糙集理论已经在基因选择、机器学习、数据挖掘、图形图像、大数据、天气预测等诸多领域得到广泛应用[17-18]. 粗糙集中的特征选择涉及特征重要度的计算,主要的度量特征工具有信息熵[19]、粗糙熵[20]与知识粒度[21]. 然而,这些度量大都基于离散型的数据集,对于连续型的基因数据集并不适用.
为此,针对基因数据集的高维、连续及不确定性特点,提出融合Filter方法与Wrapper方法的混合基因选择方法. 该方法采用邻域粗糙集粒化基因数据,定义邻域熵构造Filter筛选函数,对基因进行预选择,然后采用邻域粗糙集对预选择的基因进行特征选择,同时引入蚁群优化算法,获取个数最小的特征基因子集. 最后,对选取的特征子集采用经典分类算法测试其分类效果.
1 邻域粗糙集模型与基因选择
Pawlak粗糙集模型主要处理离散型的数据集,利用等价关系对对象集合进行划分,形成等价类知识. 针对连续型的基因表达数据集,需要预先进行离散化,而离散化过程不可避免降低了分类精度. 为此,针对连续型的基因数据,采用邻域粗糙集模型[22]进行邻域粒化,构造参数化的邻域类,用于基因子集选择.

定义2给定基因信息系统S=(U,A,V,f,δ),对于任一样本x,y∈U, 基因子集B⊆A,B={a1,a2, …,an},定义B上的距离度量函数DB(x,y)为:
其中: 当p=1时,称为曼哈顿距离; 当p=2时,称为欧氏距离.

定义4设S=(U,A,V,f,δ)为一基因信息系统,δ为邻域参数,在基因子集B⊆A上定义邻域关系NRδ(B):
U/NRδ(B)称为论域U的一个邻域覆盖.
定义5定义T=(U,C∪D,V,f,δ)为一个基因分类表,其中U表示病人样本集;C表示基因集,C值为连续型的基因表达数据; 邻域参数为δ∈[0, 1],其邻域覆盖为U/NRδ(C)={X1,X2, …,Xm};D是肿瘤分类特征,其为离散型的分类数据,肿瘤分类特征表示癌症肿瘤的分类信息,其等价类划分为U/D={Y1,Y2, …,Yn}.
定义6设T=(U,C∪D,V,f,δ)为一个基因分类表,∀B⊆C,X⊆U,记U/NRδ(B)={B1,B2, …,Bi}. 则称B*(X)δ=∪{Bi|Bi∈U/NRδ(B),Bi⊆X}为X关于B的邻域下近似集; 称B*(X)δ=∪{Bi|Bi∈U/NRδ(B),Bi∩X≠∅}为X关于B的邻域上近似集.
邻域上、下近似集组成的序对〈B*(X)δ,B*(X)δ〉用来逼近X确定集合,称为X的邻域粗糙集.

定义8设基因分类表T=(U,C∪D,V,f,δ),∀b∈B⊆C,γB(D)δ=γB-{b}(D)δ,则b是B中冗余的基因; 否则b为B中必要的基因. ∀B⊆C,若∀b∈B都是必要的基因,则称B相对于D是独立的.
定义9设基因分类表T=(U,C∪D,V,f,δ),∀B⊆C,γB(D)δ=γC(D)δ且B相对于D是独立的,则称B是C相对于D的特征基因组.
特征基因组是区分度较高的基因组成的集合,基因选择的过程就是寻找特征基因组的过程. 在一个基因分类系统中,特征基因组存在多个,其中基因个数最小的特征基因组称为最小特征基因组.
2 基于邻域熵与蚁群优化的属性约简
在邻域粒化后的基因数据集中引入邻域熵的定义,度量基因数据的不确定性,并证明邻域熵的单调性,用于基于邻域粗糙集模型的基因选择当中. 以邻域熵作为启发式信息,引入蚁群优化算法,进一步设计了基于邻域熵与蚁群优化的基因选择算法.
2.1 邻域熵的定义及单调性原理

其中: |·|表示集合当中元素的个数.


定理2设S=(U,A,V,f,δ)为一个基因信息系统,若Q⊆P⊆A,则Hδ(Q)≥Hδ(P).

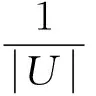
由
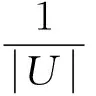
可知
由
可知
因此,Hδ(Q)≥Hδ(P)成立.
定理2表明邻域熵具有单调性,随着基因的增加单调递减,因此可用来度量基因信息系统的不确定性.
2.2 基于邻域熵的基因预选择
通过基因阵列技术得到大量基因的表达值,基因个数成千上万,其中多数基因与肿瘤分类相关性不大,对肿瘤的分类贡献也小. 定理2证明了基因个数的增减与邻域熵的大小存在着单调递减的关系. 邻域熵越小,其不确定增大,该基因则更重要. 由此,先采用基于邻域熵的过滤法对基因进行预选择,该方法按照邻域熵从小到大进行排序,选择前面n个邻域熵最小的基因作为预选特征基因组. 然后,提出基于蚁群优化的邻域粗糙集基因选择方法,对预选择的n个基因进行最小特征基因组的选取. 考虑到后续基因选择的算法运行时间,实验中n取值为100,即选择前面100个邻域熵最小的基因作为预选特征基因组.
2.3 基于蚁群优化的基因选择
科学家通过对蚂蚁觅食行为的观察与研究,发现蚂蚁在觅食过程中会释放信息素,当蚂蚁经过一条路径时,其信息素和蚂蚁的数量成正比,后面尾随的蚂蚁选择该路径的概率就更大,最后收敛到最短路径. Jensen[23]将蚁群优化算法用于求解特征选择问题. 为了加快搜索的速度,在蚁群的搜索过程中增加启发式信息.
1) 基于邻域熵的启发式信息. 下面定义基于邻域熵与分类精度加权的特征基因重要度概念,并在基于蚁群优化的基因选择过程中作为启发式信息.
定义11设基因分类表T=(U,C∪D,V,f,δ),∀a∈C,R⊆C,设t时刻,某只蚂蚁已选择了基因组R(处于i基因位置),接下去按照启发信息选择a基因(处于j基因位置),定义启发信息为a相对于基因组R的特征基因重要度,表示为:
ηij(t)=|MR∪{a}(D)δ|-|MR(D)δ|
其中:MR(D)δ=γR(D)δ·(1-Hδ(R)); |·|表示集合当中元素的个数.
2) 信息素的计算. 当某只蚂蚁经过一条路径时,其信息素随着蚂蚁的数量而增强. 设t时刻(第t次迭代),共有n只蚂蚁经过基因i到基因j上的路径,则该路径上的信息素计算如下:
其中:q为常数;R(t)表示t时刻已选取的基因组(暂时的全局最优解).
3) 局部解的求解 . 在蚁群优化算法中,每只蚂蚁分别构建一个局部解,然后根据蚁群的正反馈机制获得全局最优解. 最初蚂蚁随机初始化选择某个基因,而后根据计算的概率选择基因,其概率计算公式定义为:
其中:k表示某只蚂蚁,t表示某次迭代;τij和ηij分别表示基因i到基因j路径上的信息素和启发信息,以特征基因重要度作为启发信息; 参数α>0和β>0分别表示信息素和启发信息的重要性程度. 信息素体现全局搜索的信息,启发式信息体现局部搜索的信息. 参数α和β取值范围为0~1,其中α=1-β. 若α>β,则蚂蚁选择基因路径时主要考虑全局因素,那么收敛的时间较长,更容易获得全局解; 反之,则主要考虑局部因素,收敛的速度快,但可能更容易陷入局部解; allowedk表示可供选择的基因.
4) 信息素更新规则. 当所有的蚂蚁都分头搜索到一个局部解后,则一次迭代完成,相邻接基因边的信息素需要更新,其更新规则为:
τij(t+1)=ρτij(t)+Δτij(t)
其中:t表示迭代次数,τij(t)表示t时刻基因i到基因j边的信息素;ρ(0<ρ<1)为常量,代表信息素的挥发程度; Δτij(t)表示新增加的挥发信息素总量.
5) 搜索停止条件. 蚂蚁搜索过程停止的条件为:
a) 当γRk(D)δ=γC(D)δ,则找到了一个局部解,Rk为表示某个基因子集.
b) 若某只蚂蚁找的局部集的基数大于全局最优解基因子集的基数,则该蚂蚁就停止搜索,否则,该基因子集作为暂时的全局最优解.
c) 当达到最大迭代次数或所有的蚂蚁搜索都停止后,则算法终止,输出全局最优解; 否则,更新信息素,开始下次迭代.
2.4 基于邻域熵与蚁群优化的基因选择算法
以邻域熵为启发信息,根据蚁群优化的原理,设计基于邻域熵与蚁群优化的基因选择算法,其算法步骤描述如下:
算法1. NEACOGS(neighborhood entropy and ACO based gene selection).
输入:经过预选择后的基因分类系统T′=(U,C∪D,V,f,δ),最大迭代次数maxcycle,参数α.
输出:最小特征基因组Gmin和其基数Lmin.
步骤1 系统初始化Gmin=C,Lmin=|C|.
步骤2 计算基因分类系统的分类精度γC(D)δ|POSC(D)δ|/|U|.
步骤3 若t 步骤3.1 构造k只蚂蚁,Gk=Φ; 步骤3.2 初始化k只蚂蚁,让其随机选择某个基因ak,Gk=Gk∪ak; 步骤3.3 每只蚂蚁分布循环执行步骤3.3.1-3.3.2: 步骤3.3.2 若γGk(D)δ=γC(D)δ或者|Gk|≥Lmin,则第k只蚂蚁停止搜索; 步骤3.4 若γGk(D)δ=γC(D)δ并且|Gk|≥Lmin,则Gmin=Gk,Lmin=|Gk|; 步骤3.5 根据公式τij(t+1)=ρτij(t)+Δτij(t)更新信息素. 步骤4 输出最优基因子组Gmin和其基数Lmin. 蚁群优化搜索策略具有很好的全局寻优能力,该算法虽然不能保证找到最小特征基因组,但大部分情况下能够找到最小特征基因组. 算法NEACOGS的时间复杂度主要涉及邻域类的计算,文献[24]采用桶装排序将邻域类的计算降为线性,有效降低了算法的时间复杂度. 除了邻域类的计算之外,外层循环还有迭代次数和蚂蚁个数. 因此,算法NEACOGS的时间复杂度为O(k×t×m×n). 其中,k为蚂蚁数;t为迭代次数;m为基因个数;n为样本个数. 为验证该算法的有效性,实验中采用两个基因数据集,分别为Lymphoma和Liver cancer. 数据集Lymphoma有96个样本,4 026个基因. 其中, B-celllymphoma类别的样本42个,Other type类别的样本54个. 数据集Liver cancer有156个样本,1 648个基因. 其中, HCCs类别的样本82个,Nontumor livers类别的样本74个. 基因数据集的具体信息描述如表1所示. 表1 基因数据集 数据预处理主要是对缺失数据的补齐和对原始数据的标准化. 对于原始数据中存在缺失的情况,实验中采用均值补齐缺失的数据,并采用如下公式对原始基因数据进行标准化,将数据标准化为[0, 1]区间: 其中:gij表示编号为i的病人样本在第j个基因上的基因表达值; max(gj)、min(gj)分别表示第j个基因上的最大、最小表达值. 基因数据经过标准化后,为[0, 1]区间连续型的数据. 基因个数庞大,往往成千上万. 实验中先进行预选择,计算每个基因的邻域熵值,并按照邻域熵值从小到大排序,选取前面100个基因做为预选择后的基因组. 实验过程采用文献[25]中基于粗糙集的特征选择算法TRS、文献[26]中基于邻域的特征选择算法NRS以及本研究算法NEACOGS进行比较. 对于经典粗糙集特征选择算法TRS的离散化过程采用文献[27]中的方法,而基于邻域的特征选择算法NRS与算法NEACOGS,不需要离散化,但需给定邻域参数,实验中设邻域参数为δ=0.1. 本研究算法实验中蚂蚁个数设定为预选择基因组中基因个数的三分之一,为k=33,最大迭代次数maxcycle=100,权重参数α=0.3. 两个基因数据集经过预选择后,都保留了100个基因,在此基础上采用3种不同的特征选择算法进行基因选择,实验结果如表2所示. 表2 基因选择实验结果 由表2可知,TRS算法在Lymphoma数据集中选择的基因子集含有7个基因,在Liver cancer数据集中选择基因子集含有6个基因. NRS算法在Lymphoma数据集中选择的基因子集包括了6个基因,在Liver cancer数据集中选择的基因子集包括5个基因. 而本研究算法在Lymphoma数据集中选择出5个特征基因,在Liver cancer数据集中也选择出5个特征基因. 从时间上比较,可知NRS算法与TRS算法比较接近,TRS略好于NRS. 这两个算法都是采用启发式搜索一遍,找到次优解. 而蚁群算法是多次迭代,因此NEACOGS算法的时间复杂度较高,但是更容易找到最优解. 下面再比较被选基因子集的分类能力,分别采用KNN、C5.0分类器进行分类实验,并用留一交叉法检验分类正确率,实验结果如表3所示. 表3 基因分类精度 上述实验结果表明,基于经典粗糙集的基因选择方法(TRS)、基于邻域关系的基因选择方法(NRS)和基于邻域熵与蚁群优化的基因选择方法(NEACOGS)都能正确提取有效的基因子集. 在NRS和NEACOGS算法中不需要离散化,由于避免了离散化过程造成的信息丢失,提取的特征基因个数较少. 而NEACOGS算法进一步采用了蚁群优化的搜索策略,得到了更小的基因子集. 通过在三种算法选取的基因子集上分别进行分类实验,实验结果表明都取得了较好的分类精度,而且分类精度相差较小,主要是因为三种算法都采用了基于邻域熵筛选后的数据集. 本研究重点分析了基因分类中的关键问题——基因选择方法,提出了基于邻域熵与蚁群优化的基因选择方法,并在2个基因表达数据集上进行了实验. 首先,针对传统粗糙集特征选择方法难以处理连续型基因数据的缺点,引入邻域粗糙集模型,定义邻域熵度量数据的不确定性,对高维基因数据集进行筛选,大量减少基因个数. 然后,在邻域粗糙集基因选择理论的框架中引入蚁群优化搜索策略,提出基于邻域熵与蚁群优化的基因选择,并给出了适用于特征基因选择的具体算法. 该算法充分利用邻域熵度量不确定性数据方面的优势,定义基于邻域熵的特征基因重要度作为启发式信息,加速算法收敛过程,并发挥蚁群优化算法的全局寻优性能,获取最优基因子集. 目前,采用蚁群优化与邻域粗糙集融合的方法进行特征基因选择的研究还很少见,本研究拓展了粗糙集理论研究的应用范围,为基因选择研究提供了一条新的途径. [1] LI S T, WU X X, HU X Y. Gene selection using genetic algorithm and support vectors machines[J]. Soft Computing, 2008, 12(7): 693-698. [3] 张军英, WANG Y J, KHAN J, 等. 基于类别空间的基因选择[J]. 中国科学(E 辑), 2003, 33(12): 1 125-1 137. [4] DASH M, LIU H. Feature selection forclassification[J]. Intelligent Data Analysis, 1997, 1 (1): 131-156. [5] SAEYS Y, INZA I, LARRANAGA P. A review of feature selection techniques inbioinformatics[J]. Bioinformatics, 2007, 23(19): 2 507-2 517. [6] GUYON I, ELISSEEFF A. An introduction to variable and featureselection[J]. Journal of Machine Learning Research, 2003, 3(6): 1 157-1 182. [7] KIRA K, RENDELL L A. The feature selection problem: traditional methods and a new algorithm[C]//Proceedings of the Tenth National Conference on Artificial Intelligence. San Jose: AAAI, 1992: 129-134. [8] MIAO D Q, HOU L. A comparison of rough set methods and representative inductive learningalgorithms[J]. Fundamenta Informaticae, 2004, 59 (2/3): 203-219. [9] KOHAVI R. Feature subset selection using the wrapper method: overfitting and dynamic search space topology[C]//Proceedings of the First International Conference on Knowledge Discovery and Data Mining. Montreal: AAAI, 1994: 109-113. [10] LIN S W, LEE Z J, CHEN S C,etal. Parameter determination of support vector machine and feature selection using simulated annealing approach[J]. Applied Soft Computing, 2008, 8(4): 1 505-1 512. [11] CHEN Y M, MIAO D Q, WANG R Z. A rough set approach to feature selection based on ant colonyoptimization[J]. Pattern Recognition Letters, 2010, 31(3): 226-233. [12] DORIGO M, MANIEZZO V, COLORNI A. Ant system: optimization by a colony of cooperatingagents[J]. IEEE Trans Syst Man Cybernetics-Part B, 1996, 26(1): 29-41. [13] ZHANG X L, CHEN X F, HE Z J. An ACO-based algorithm for parameter optimization of support vectormachines[J]. Expert Systems with Applications, 2010, 37(9): 6 618-6 628. [14] LIAO T J, THOMAS S, MARCO A,etal. A unified ant colony optimization algorithm for continuous optimization[J]. European Journal of Operational Research, 2014, 234(3): 597-609. [15] JUNIOR L, NEDJAH N, MOURELLE L. Routing for applications inNoC using ACO-based algorithms[J]. Applied Soft Computing, 2013, 13(5): 2 224-2 231. [16] PAWLAK Z. Roughsets[J]. International Journal of Computer and Information Science, 1982, 11(5): 341-356. [17] JENSEN R, SHEN Q. Finding rough setreducts with ant colony optimization[C]//Proceedings of the UK Workshop on Computational Intelligence. Bristol: [s.n.], 2003: 15-22. [18] TABAKHI S, MORADI P, AKHLAGHIAN F. An unsupervised feature selection algorithm based on ant colony optimization[J]. Engineering Applications of Artificial Intelligence, 2014, 32: 112-123. [19] 苗夺谦, 王珏. 粗糙集理论中概念与运算的信息表示[J]. 软件学报, 1999, 10 (2) : 113-116. [20] PALSANKAR K, UMASHANKAR B, PABITRA M. Granular computing, rough tropy and objectextraction[J]. Pattern Recognition Letters, 2004, 26(16): 2 509-2 517. [21] 苗夺谦, 范世栋. 知识的粒度计算及其应用[J]. 系统工程理论与实践, 2002, 22(1): 48-56. [22] HU Q H, YU D R, XIE Z X. Neighborhood classifiers[J]. Expert Systems with Applications, 2008, 34(2): 866-876. [23] JENSEN R. Combining rough and fuzzy sets for feature selection[D]. Edinburgh: The University of Edinburgh, 2005. [24] LIU Y, HUANG W L, JIANG Y,etal. Quick attribute reduct algorithm for neighborhood rough set mode[J]. Information Sciences, 2014, 271(7): 65-81. [25] 王国胤. Rough 集理论与知识获取[M]. 西安: 西安交通大学出版社, 2001. [26] HU Q H, YU D R, LIU J F,etal. Neighborhood rough set based heterogeneous feature subset selection[J]. Information Sciences, 2008, 178(18): 3 577-3 594. [27] 苗夺谦. Rough Set理论中连续属性的离散化方法[J]. 自动化学报, 2001, 27(3): 296-302.3 实验分析

3.1 数据预处理与预选择
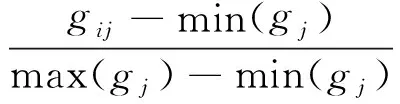
3.2 实验结果与分析


4 结论

