微分算子法在处理线性微分方程通解理论中的应用

林庆泽

（广东工业大学 应用数学学院，广东 广州 510520）

0 引言

微分算子法是近代发展起来的一种以代数观点处理分析问题的重要方法。著名数学家L.Hörmander在其长达4卷的名著中对线性偏微分算子作出了极为系统的论述并以其为工具在偏微分方程的一般理论上取得了一系列突破性的成果[1]。

本文在文献[2]和[3]的基础上，引进多项式算子并对经典的线性微分方程通解理论进行了更为系统的总结和发展，得到了一些关于线性微分方程及其方程组通解理论的新成果。该方法具有较为明显的系统性和连贯性，从而对学习和研究线性微分方程通解理论具有一定的指导性和启发性。

1 微分算子法的理论基础

定义1对于n次多项式称为n阶多项式微分算子（简称多项式算子）。

对于所有的多项式算子组成的集合{P（D）}，文献[3]已阐明在对多项式算子P（D）进行运算时，可以将微分算子D视为变量x，从而进行与多项式P（x）的加法、减法和乘法形式一样的运算。因此有：

命题1[4]对于任一α∈C(复数域)，有下面的Taylor公式：

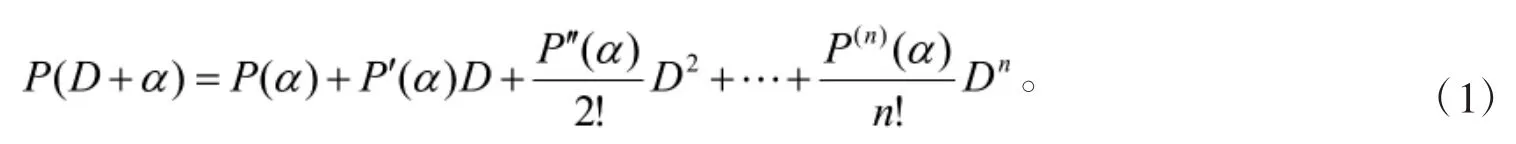
命题2[4]对于任一α∈C及任一n次连续可微函数h(x)，有：

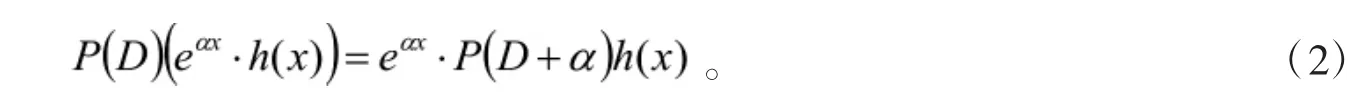
定义2算子称为P(D)的逆算子，如果

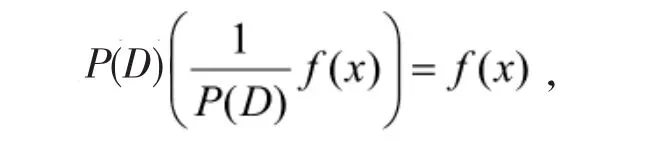
下面证明逆算子的若干基本结论：

命题3若P(D)是一阶的，即P(D)=D+α，α∈C（复数集），则

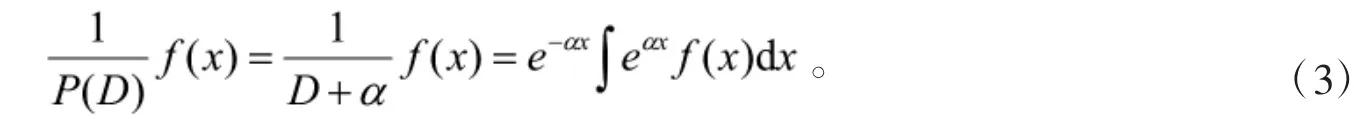
证明由命题得证。

命题4若α∈C是P(x)=0的k重根，则

证明由命题1和命题2，

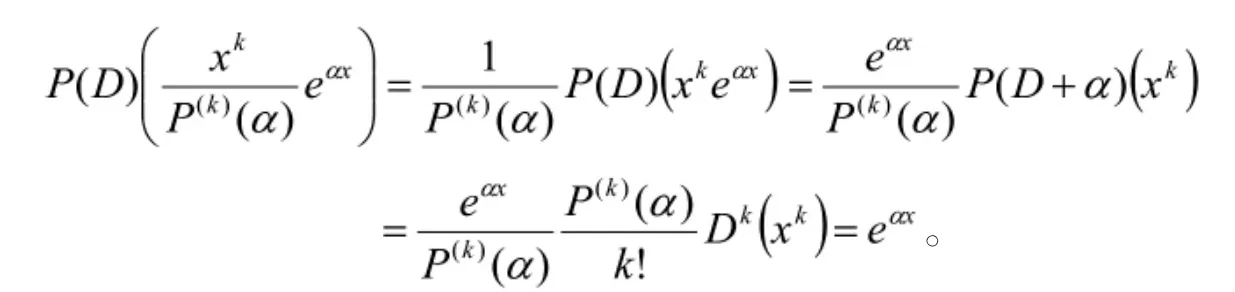
命题5

证明由命题2，，命题得证。

容易证明：

命题6假设P(D)为实系数多项式算子，若，（其中f1，f2，u，v皆为实函数），则

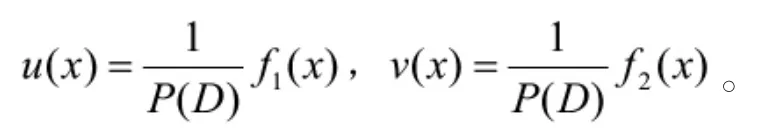
推论1假设P(D)为实系数多项式算子，则

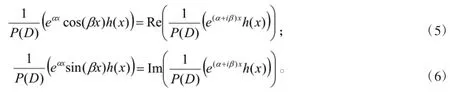
命题7若f(x)为m次多项式，P(0)=a0≠0，将多项式P(x)按x的升幂次序排列后去除1，记，其中为次数≤m的多项式，多项式R(x)的次数≥m+1，则

证明由，命题得证。

2 线性微分方程的通解问题

2.1 n阶常系数线性齐次微分方程的通解问题

对于n阶常系数线性齐次微分方程

文献[1]中通过微分算子法可将其通解问题降为求一些一阶或二阶常系数线性微分方程的通解问题：

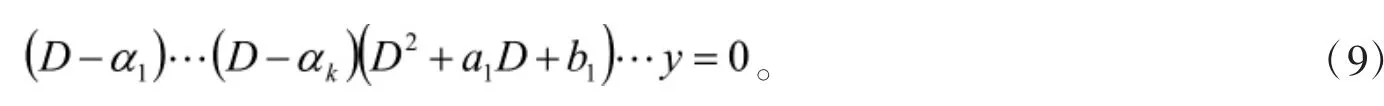
命题8若方程（8）的特征方程有根α1，α2，...，αp，其中α1为r1重根，α2为r2重根，...，αp为rp重根，则方程（8）的通解为：若αi为复根，则αi亦为复根，此时可将分别换为

2.2 常系数线性非齐次微分方程的通解问题

对于n阶常系数线性非齐次微分方程：

例1求方程的一个特解。

解这里，故

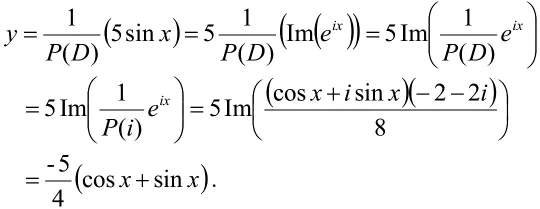
2.3 二阶变系数线性微分方程的通解问题

文献[2]利用微分算子法处理二阶变系数线性微分方程并得到了其通解与Riccati方程的通解之间的转化关系。另外利用文献[2]中的定理2，只要求得二阶变系数线性齐次微分方程的一个特解，则可得到其通解以及其对应的非齐次方程的通解。

3 常系数线性微分方程组的通解问题

对于常系数线性齐次微分方程组的通解问题已有指数函数等方法可求得基解矩阵[5-6]，由于根据线性微分方程通解理论，只需要其对应的非齐次方程组的一个特解便能求该非齐次方程组的通解。我们有下面的命题：

命题9对于常系数线性非齐次微分方程组：

则该线性微分方程组有特解：

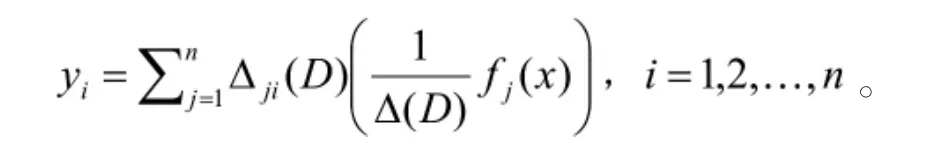
其中Δji(D)是行列式Δ(D)中元素Pji(D)代数余子式。

证明对于该方程组的系数算子增广矩阵

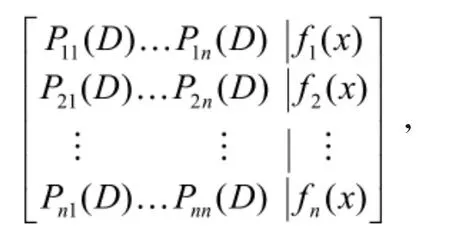
利用线性代数学知识可对该矩阵进行初等行变换从原方程组得到。但由于逆算子的不唯一性，这里我们不取，我们只取，i=1，2，...，n容易验证，这样得到的解确实是原方程组的解。

[1]HÖRMANDER L.The analysis of linear partial differential operators(I-IV)[M].New York：Springer-Verlag，2005：1-100.

[2]林庆泽.算子法在处理线性微分方程中的应用[J].兰州文理学院学报(自然科学版)，2016，30（1）：13-16.

[3]林庆泽.利用微分算子法研究二阶齐次线性微分方程与Riccati方程通解之联系[J].海南师范大学学报（自然科学版），2017，30（3）：238-244.

[4]罗亚平，陈仲.常微分方程[M].南京：南京大学出版社，1987：23-85.

[5]丁同仁，李承治.常微分方程教程[M].北京：高等教育出版社，2004：157-206.

[6]ARNOLD V I.Ordinary differential equations[M].New York：Springer-Verlag，2003：152-161.