基于gamma退化过程的装备备件保障模型

杜振东，赵建民，杨志远，倪祥龙

（军械工程学院，石家庄 050003）

0 引言

随着维修方式的不断发展，在装备日常保障中，基于状态的维修（CBM）逐渐成为了装备维修的主流方式。

目前在CBM中，对退化过程以及相关维修决策的研究已较为成熟［1-3］，但基于退化过程对备件订购时间进行决策的研究相对较少。而且，研究备件的文献也很少结合系统的退化过程进行研究。陶小创等［4］通过综合分析备件保障概率的影响因素，预测装备的备件需求量。杨仕美等［5］利用库存量与装备可用度的关系，用边际分析法对备件库存量进行优化。Zhang J等［6］和 Vander Heijden M C［7］以备件满足率为优化目标，以费用为约束研究了备件优化配置模型。赵建忠等［8］建立了改进系统备件满足率约束下的备件优化配置模型。蒋云鹏等［9］采用Armstrong等［10］提出的经典联合策略，结合 Si等［11］提出的具有参数自适应估计能力的RUL预测方法，针对带有状态监测的单部件系统，对备件的替换时间和备件的订购时间进行了联合决策。以上研究中涉及备件订购时间优化决策的研究较少，且模型计算复杂，在平时的装备备件保障中难以有效地实现工程应用。

基于此，本文针对平时装备保障中的备件保障问题，着重研究了基于gamma退化过程的备件保障模型，通过连续的状态监测信息获得部件的退化量阈值分布，结合Armstrong等［10］提出的经典联合策略，以装备维修总费用率最小为目的，决策备件订购时间。

1 模型基本假设

一般来说，系统的退化轨迹会存在差异，但仍可以通过归纳总结找到其退化规律。本文针对单系统（单部件）备件保障问题进行研究，为方便建模分析，作出如下假设：

①缺少备件所造成的停机损失费用率和库存费用率均为固定值，分别表示为ks和kh；

②备件从订货到收货的时间间隔是固定的，表示为L；

③初始时刻备件库存为零；

④备件的价格固定，不随时间而变化；

⑤备件运费计算在价格之内，为固定值，不单独考虑。

2 退化与备件订购决策模型

2.1 退化模型

某系统的退化量用Y表示，系统在t时刻的退化水平用随机变量y（t）表示，假设在初始状态时的退化量为 0，即 y（0）=0，并且在退化过程中{y（t）}t≥0是非减的，失效时间为 Tf，失效阈值为 yF，当 y（t）≥yF，t≥0时，系统退化失效。在可能的分布中，Gamma分布可以用来描述连续的累计磨损过程（Abdel-Hameed，1975），并且具有对退化过程建模所需的所有属性，既非负、平稳增长和从零开始的独立性的增量过程［12］。在实践中，退化量的均值与方差通常是随时间增长，因此，在建模中作如下假设：

假设退化过程 y（t）服从均值为 μt，方差为 σ2μt的 Gamma分布，且 y（0）=0。Gamma分布的形状参数为α，尺度参数为β，密度函数为，其中Γ（·）为Gamma函数，其均值与方差分别为αβ和αβ2。根据以上假设，在计算给定时间t时的退化量y（t）时具有以下的密度函数：

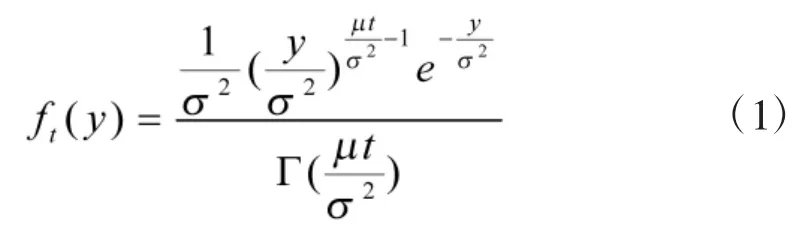
在t时刻，求退化量y在［0，y］的分布为

由于需要确定订购备件的时间，所以最后的表达式应该是一个关于时间t的表达式，所以现在要确定在某确定退化量y时从［0，t］的时间分布，记为Fy（t）

而且可知

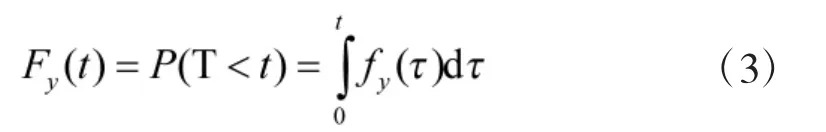
其中，fy（t）是在退化量为y时的时间t的概率密度函数。

由于系统的退化轨迹不确定，存在着多种可能，经归类可分为三类，如图1所示。

图1 Fy（t）与Ft（y）关系图

①还没到t时刻，系统的退化量就已经达到了退化量 y，如图 1 中曲线 1、2、3、4，此时退化轨迹从退化量为y时与横坐标轴平行的这条线出去了；

②在t时刻系统的退化量达到退化量y，如图1中曲线5，此时正是期望发生的情况；

③已经到了t时刻，而系统的退化量还没有达到y，如图1中曲线6、7，要想达到y就需要再经过一段时间，所以系统的退化轨迹从t时刻上与纵坐标轴平行的那条线出去了。

不论是哪种情况，退化轨迹要么从横着的退化量为y的这条线出去，要么从竖着的t时刻上的那条线出去，除此之外不会再出现其他情况，所以这两种情况相加得到的概率为1，即：

将t时刻退化量y的分布带到式（4）中，就能得到退化量为y时的时间分布

所以

2.2 费用模型

当系统达到失效阈值时对系统进行更换，这时需要考虑是否有备件。现在假定初始状态即是备件被更换上的时刻，这时候是一个周期的开始，直到这个部件达到退化阈值，再次更换为止，这个周期结束。由于发生故障的时刻不确定，所以周期的长短也不确定。本文的目的是通过研究退化规律，预测系统到达故障阈值的时间，决策在什么时候开始订购备件使总费用率最少。在周期过程中，有可能出现3种情况，如图2所示。

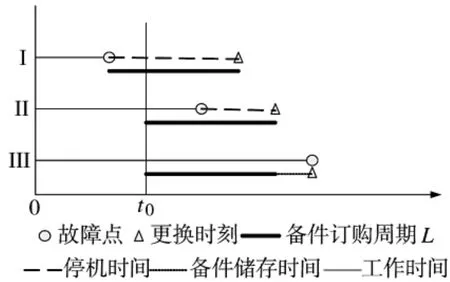
图2 备件订购时间决策示意图

I还没订购备件，系统就已经出现故障；

II已经订购备件，但是订购的备件还没到时系统出现故障；

III系统出故障时正好有备件。

如图2可知，达到退化阈值的时机不同，所产生的费用也不同。

通常来说，一旦设备停机，所产生的停机损失费会很高，远远高于备件的储存费用，即ks＞＞kh。

初始时刻为0，订购备件下单时刻t0，从下单到收到货所需的时间为L。当系统在［0，t0］区间达到退化阈值时立即下单订购备件，当系统达到故障阈值的时刻处于已经下订单到收到货之间时，不再重新下单，而是等到备件到货后立即进行更换。

系统的退化量在时间上的分布服从函数Fy（t），其密度函数为f（t）。由式（3）可知

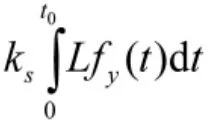
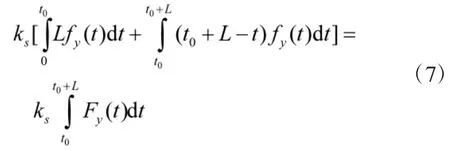
如果在t0+L的时刻部件还没有到达退化阈值，而这时备件已经到货，这时就需要对备件进行储存，储存备件会产生储存费用。在一个周期中保存备件的储存费用为：

由于系统每个不同个体之间会有差异，所以使用后到达退化阈值的时间也不同。但是可以根据其概率密度函数来求订货时间为t0，订货到收货的时间间隔为L时周期长度的期望。该部件采用的是连续的状态监测，当退化量达到退化阈值时进行部件的更换。期望的周期长度为：

在整个运行周期中，费用率最低是我们追求的目标，相应的目标函数为：

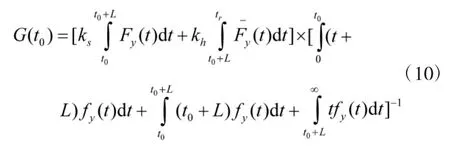
由于停机损失费用率ks要远远大于备件储存费用率kh，并且储存的时间越长费用越高，最好的状态是在系统达到退化阈值时有备件可用，而且备件正好到货或是储存的时间很短，这种状态最理想。经分析订购的太早和太晚都会使总费用增加，故费用率函数是一个先减后增的函数。求得费用率函数最低点对应的t0时刻，在该时刻订购备件，可以使总费用率最小。

3 算例分析

考虑某型装备关键件平时订货问题，该型装备备件保障过程可简要分为如下几步：

第1步：订购备件。使用单位在合适的时间将备件需求呈报上级部门，上级部门马上向厂家订货。

第2步：厂家备货。厂家需要一定的时间生产准备所订购备件。

第3步：发货运送。厂家发货后需要一定时间将备件运送至相关使用部门。

由经验可知从呈报备件需求到收到备件的间隔时间是基本固定的，变化范围很小，基本可忽略。

该型装备造价昂贵，且需要连续工作，一旦停机将造成重大的经济损失，所以要尽量保证在装备达到退化阈值时有备件。但是该备件的保存费用比较昂贵，长期储存备件会增加使用费用，而且该备件有储存寿命，不适合长期储存。所以该装备采取的方法是平时不储存备件，在装备使用一段时间后订购备件，且一次只订购一个，使备件在部件达到故障阈值时到货，这样既不会产生储存费用亦不会产生停机损失费用。

然而这只是理想情况，现实中部件的退化轨迹不会完全相同，其到达故障阈值的时刻也会不同。通过对大量退化轨迹的分析，研究其退化规律，制定合适的订货时间点，使其总费用率最小才是要解决的问题。

已知，该部件的订购价格是固定的，不随订购时间而变，运费也是固定的，其储存费用率为1000元/d，停机损失费用率为33 000元/d，退化阈值为0.1，当退化量达到0.1时即进行部件的更换。从呈报备件需求到收到货的时间是45d。由大量的该部件退化数据求得μ=0.000 2/d，σ2=0.02。将这些数据带入本文所建模型，采用小步长积分法进行近似计算，求得订货时间和费用率的关系如图3所示。

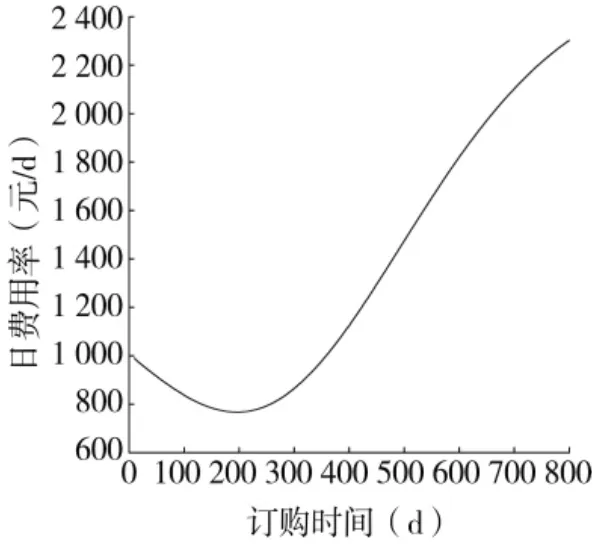
图3 备件订购时间与日费用率之间的关系图

经过对图中数据进行分析，最小费用率为767.698 6元/d，最佳的订货点是运行196 d的时候订货，此时的费用率最小，提前或推后都会使费用率增加。

从所有数据中，按每隔10 d取一个数据的方式，取100 d～400 d时的数据，给出如表1。

将所给数据绘制成折线图，如图4（横坐标为天数，单位：d；纵坐标为费用，单位：元；范围:100 d～400 d）。

可以看出，保存费用随着订货时间的推迟而下降，损失费用随着订货时间的推迟而增高，但是总费用确是先下降后上升的过程。由图3（横坐标为天数，单位：d；纵坐标为费用率，单位：元/d）可以看出费用率也是先下降后上升的过程，总费用和费用率几乎在同时达到最低点，这就是实际中想要的结果。通过这个实例可以证明在实际应用中，使用本文所建模型进行备件订购时间的决策，可以有效减少备件储存和使用过程中的总费用和费用率。

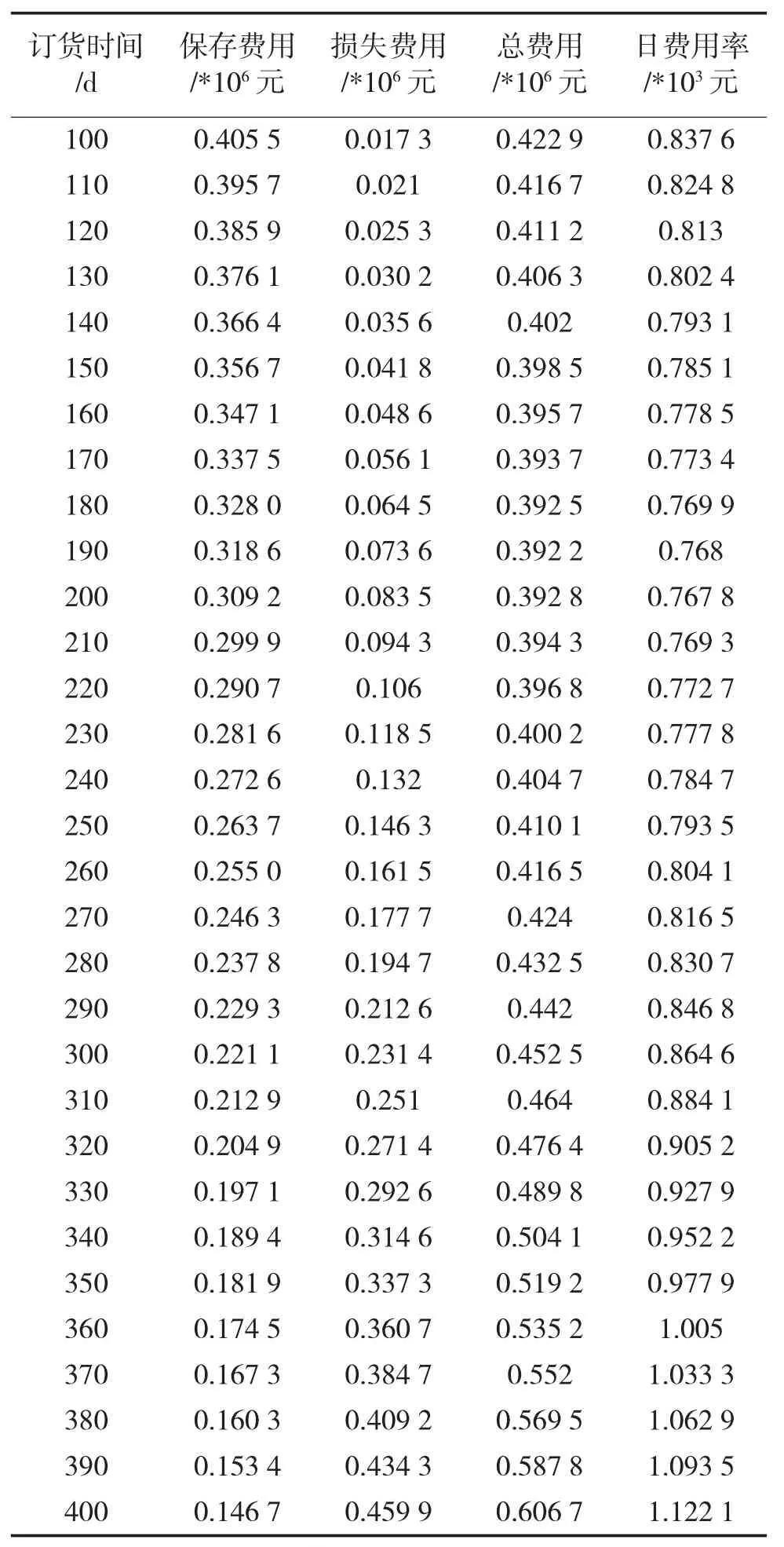
表1 各项费用数据表

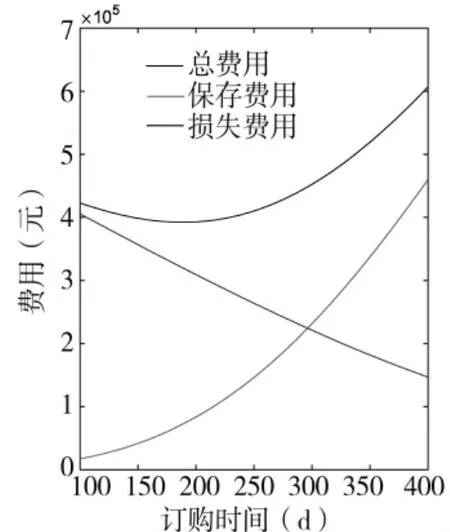
图4 各项费用变化曲线图

4 结论

本文研究了基于gamma退化过程的备件订购问题。通过对部件建立gamma退化模型，经推导计算得到任意退化量下的使用时间分布，将该退化模型与改进的费用率模型联合使用，在费用约束条件下，决策了最优备件订购时间，使费用率最小。并且通过案例分析对该模型进行了验证。所得结果表明，该模型在实际备件订购过程中确实有应用价值，在所决策的时间内订购备件确实能降低总费用，使费用率最低。过早和过晚都会使费用率增加。

［1］葛小凯，胡剑波，张博锋.退化系统状态维修决策与维修活动建模 ［J］ 系统工程与电子技术，2013，35（1）：102-108.

［2］谷玉波，贾云献，张英波.基于Gamma退化过程的剩余寿命预测及维修决策优化模型研究［J］.轴承，2013（4）：44-49.

［3］石慧，王玉华，曾建潮.MRO系统动态维修策略的建模与优化［J］.火力与指挥控制，2012，37（6）：181-187.

［4］陶小创，郭霖翰，肖波平，等.基于备件保障概率分配的备件需求量预测模型［J］.兵工学报，2012，33（8）：975-979.

［5］杨仕美，石忠义，翟旭升，等.基于重要度的航材备件库存综合优化模型 ［J］.火力与指挥控制，2014，39（8）：109-113.

［6］ ZHANG J，ZHANG J.Fill rate of single-stage general periodic review inventory systems［J］.Operations Research Letters，2007，35（4）：503-509.

［7］VANDER H M C.Near cost-optimal inventory control policies for divergent networks under fill rate constraints［J］.Inte-ernational Journal of Production Economics，2000，63（2）：161-179.

［8］赵建忠，李海军，叶文，等.改进系统备件满足率约束条件下的备件优化配置建模 ［J］.兵工学报，2013，34（9）：1187-1192.

［9］蒋云鹏，郭天序，周东华.基于剩余使用寿命预测的替换时间和备件订购时间联合决策［J］.化工学报，2015，66（1）：284-290.

［10］ARMSTRONG M J，ATKINS D R.Jointoptimization of maintenance and inventory policies for a simple system［J］.IIE Transaction，1996，28（5）：415-424.

［11］SI X，WANG W，CHEN M.Adegradation path-dependent approach for remaining useful life estimation with an exact and closed-form solution ［J］.European Journal of Operational Research，2013，226（1）：53-66.

［12］贾希胜.以可靠性为中心的维修决策模型［M］.北京：国防工业出版社，2007.