基于改进蜂群算法的雷达网目标分配方法*
王 蓉,周雪梅
(1.九江职业技术学院电气工程学院,江西 九江 332007;2.哈尔滨工程大学自动化学院,哈尔滨 150001)
0 引言
随着新型武器和航天技术的不断发展,单部雷达不论在监测能力上,还是电子防御功能上都有较大的局限性[1]。利用雷达网技术则能有效提高雷达系统的整体性能,当目标来袭时,雷达网可以实现信息交流与共享,有效提高对目标的识别和跟踪能力。雷达网多目标分配是雷达兵部队作战的核心任务,在保证完成对空监视任务的前提下,针对于雷达网的多目标分配具有十分重要的军事意义[2]。雷达网多目标分配可看作是一个NP问题,近年来,人们开始应用群集智能算法对这一问题优化求解。文献[3]提出了一种基于萤火虫算法的雷达目标分配方法,该方法将雷达目标分配问题分解为多维背包问题,使用人工萤火虫群优化算法对目标函数进行寻优并确定分配策略,收敛速度快,求解的结果稳定;文献[4]提出将遗传算法用于雷达目标分配,求解速度快,能够为指挥员做出正确的目标分配方案;文献[5]将改进遗传应用于雷达目标分配,相比于基本遗传算法,直观且操作简单,算法的收敛速度加快。
对比上述几种方法可知,提高算法稳定性和收敛速度、增强算法的寻优能力在雷达网目标分配中具有十分重要的意义。因此,本文对雷达网数学模型进行了优化,对蜂群算法作出改进,提出采用改进的蜂群算法对雷达网目标问题进行优化求解。相对于其他算法,蜂群算法具有操作简单、全局寻优能力强和收敛速度快等优点[6],改进后的人工蜂群算法寻优能力进一步增强,在解决雷达网目标分配问题时展现出了良好的应用前景。
1 建立数学模型
决定雷达监视能力σ的因素主要有:雷达性能αi1、雷达部署位置 αi2、雷达监视区域 αi3、雷达频率带宽 αi4、雷达抗干扰能力 αi5[7]。以上几个因素对雷达优先级的影响是不同的,通常使用权系数来反映因素的影响程度,由此构造雷达的监视能力σi函数为:
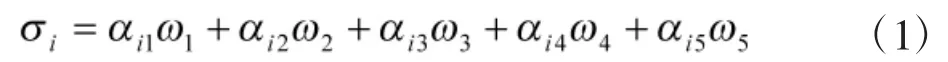
决定目标威胁程度f的因素主要有:目标性能βj1、目标距离 βj2、目标速度 βj3、目标来袭角度 βj4、目标飞行高度 βj5、双方态势 βj6[11],构造目标的威胁程度fi函数为:
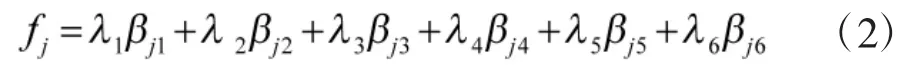
雷达网对来袭目标的监视能力最大为:

式中,xij表示雷达si对目标tj的分配关系,0表示不分配,1表示分配;pij为雷达si对目标tj的监视效用。
雷达网对来袭目标进行识别和跟踪能力最小为:

式(5)中,约束条件1保证了雷达在监视能力范围内进行监视,其中Mi为雷达si可同时监视的目标tj的数目。约束条件2保证了每个目标都会被识别和跟踪。
2 改进蜂群算法
蜂群算法由印度学者Karaboga于2005年提出,是一种模拟蜜蜂采蜜行为的新型群体优化算法[8-10]。算法的蜜源代表雷达网多目标分配方案,蜜源质量(适应度值)代表其收益度,为待优化函数,寻找最优解就是寻求质量最高的蜜源。
蜂巢内共有4种蜜蜂:采蜜蜂、引领蜂、跟随蜂、侦查蜂;每种角色的蜜蜂分担不同的工作,相互协作,角色之间在一定条件下进行相互转换[11]。
4种蜜蜂的关系如图1所示[12]:
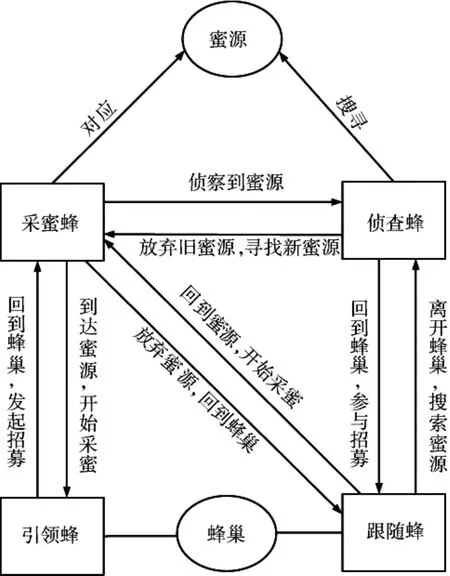
图1 蜜蜂关系转化示意图
2.1 构造适应度函数
设蜜源X为m×n阶矩阵。

雷达对目标的监视能力P为m×n阶矩阵,pij为雷达si对目标tj的监视效用。
适应度函数S(X)计算方法如式(10)所示:

2.2 改进蜂群算法
在蜂群算法中,跟随蜂按照蜜源概率值采用轮盘赌的方式选择蜜源,在选择更新时需要计算当前N个引领蜂所在的蜜源各自的信息概率值 Qk,即

可以看出,跟随蜂基于贪婪选择机制选择蜜源,蜜源的适应度S(X)值越大越有可能被选中更新,得到的跟随蜂数目越多。但是,概率值Qk较小的蜜源周围也可能存在最优解,因此,随着计算次数增加,种群多样性下降,算法过早收敛,易陷入局部最优。
针对上述问题,对基本蜂群算法作出改进。在改进蜂群算法中,采用双向轮盘赌的策略,当引领蜂对跟随蜂进行招募时,N个跟随蜂根据式(8)采用轮盘赌的方式选择引领蜂,另外有N个跟随蜂根据式(9)采用反向轮盘赌的策略选择引领蜂[13]。
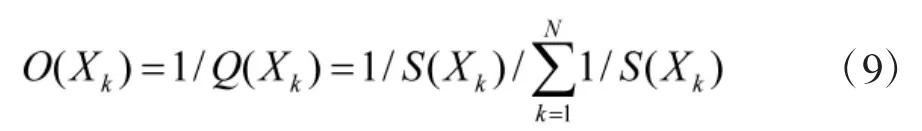
从式(9)可以看出,根据反向轮盘赌的选择规则,适应度S(X)越小的蜜源被跟随蜂选择的概率就越大,从而得到的跟随蜂越多。
采用双向轮盘赌的策略,可以使蜂群算法朝着两个方向进化,既保证在每一次迭代中选择适应度最好的蜜源,又同时保留了适应度较低的蜜源,维持了种群多样性,降低了陷入局部最优的可能性,进一步提高了算法的全局寻优能力。
2.3 算法步骤
Step 1:设置算法的主要参数:蜂群规模NP、算法最大迭代次数MCN、参数Limit。
Step 2:随机生成N个蜜源,并按照式(7)计算每个引领蜂所对应蜜源的适应度值。
Step 3:采蜜蜂开始对某一个蜜源进行更新,如果该蜜源未更新计数器次数达到预设次数,则舍弃旧蜜源生成新蜜源;否则,继续更新。置当前迭代次数为1。
Step 4:判断该蜜源的更新次数是否达到预设更新次数,若是,则对下一个蜜源进行更新;否则该蜜源继续更新。
Step 5:重复Step 4直到N个蜜源更新完毕。
Step 6:如果迭代次数小于最大迭代数MCN,转到下一步骤;否则,转到Step 10。
Step 7:采蜜蜂回到蜂巢,变为引领蜂,招募跟随蜂。
Step 8:N个跟随蜂根据式(8)采用正向轮盘赌选择机制来选择引领蜂;N个跟随蜂根据式(9)采用反向轮盘赌选择机制来选择引领蜂。
Step 9:蜜蜂回到蜜源,转Step 3,迭代次数加1。
Step 10:迭代终止,输出最优值。
3 仿真实验
给定某雷达部队的雷达网中共有12部雷达,来袭目标共有7个,每个目标的威胁程度不同。雷达监视能力、目标的威胁度以及各雷达对目标的监视能力见表1。在仿真实验中,设置算法的最大迭代次数MCN=2 000,未更新计数器阈值为20,蜜蜂个数NP=75,蜜源预设更新次数为50次。
3.1 蜂群算法改进前后雷达网目标分配方案对比

图2 蜂群算法改进前后收敛曲线对比图

表2 最优目标分配方案
由图2可知,基本人工蜂群算法在迭代1 652次达到稳定,得到的最优目标分配方案的适应度为0.628 1;而改进人工蜂群算法在迭代1 162次后便达到稳定,得到的最优目标分配方案的适应度为0.636 9。由此可知,蜂群算法可有效解决雷达网目标分配问题,但改进后的蜂群算法收敛快,能够有效地防止陷入局部最优解,得到的最优目标分配方案适应度更高。
3.2 蜜蜂个数改变前后雷达网目标分配方案对比

图3 密峰个数改变前后收敛曲线对比图
由图3可知,蜜蜂个数为60个时,迭代1 555次达到稳定,得到的最优目标分配方案的适应度为0.620 4;蜜蜂个数为75个时,迭代1 526次便达到稳定,得到的最优目标分配方案的适应度为0.624 5。说明适当增加算法中的蜜蜂数目,算法收敛速度加快,得到的最优目标分配方案适应度更高。
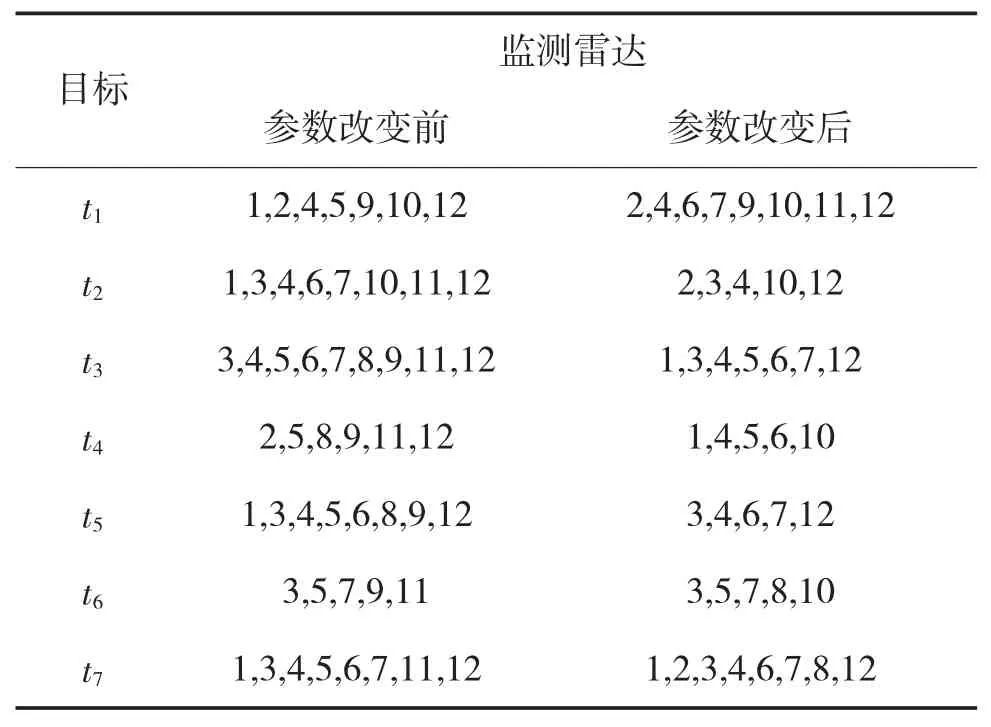
表3 最优目标分配方案
3.3 未更新计数器阈值改变前后目标分配方案对比
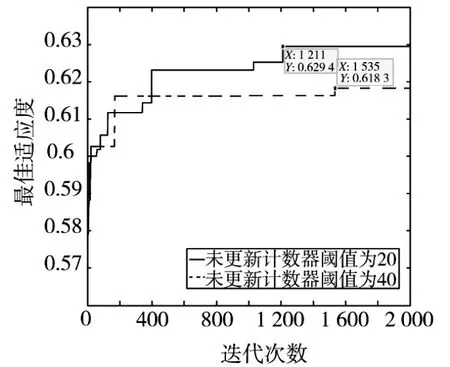
图4 未更新计数器阈值改变前后收敛曲线对比图

表4 最优目标分配方案
由图4可知,未更新计数器阈值为20时,迭代1 211次达到稳定,得到的最优目标分配方案适应度为0.629 4;未更新计数器阈值为40时,迭代1 535次才达到稳定,得到的最优目标分配方案适应度为0.618 3。说明适当降低未更新计数器阈值,算法收敛速度加快,得到的最优目标分配方案适应度更高。
3.4 蜜源预设更新次数改变前后目标分配方案对比
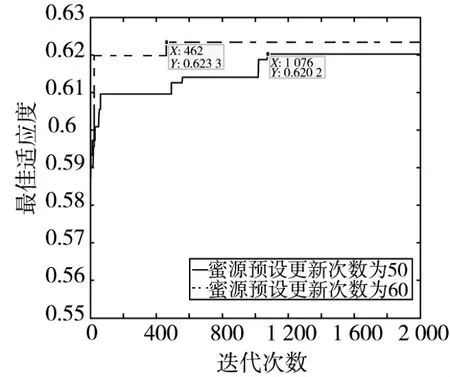
图5 蜜源预设更新次数改变前后收敛曲线对比图

表5 最优目标分配方案
由图5可知,蜜源预设更新次数为50时,迭代1 076次达到稳定,得到的最优目标分配方案适应度为0.620 2;蜜源预设更新次数为60时,迭代462次便达到稳定,得到的最优目标分配方案适应度为0.623 3。说明适当增加蜜源预设更新次数,算法收敛速度加快,得到的最优目标分配方案适应度更高。
此外,在仿真实验中,得到的最优目标分配方案并不相同,说明算法在初始化过程中随机生成的N个蜜源对最优目标分配方案有一定影响。
4 结论
本文提出了基于改进蜂群算法的雷达网目标分配方法,利用改进蜂群算法对目标函数进行寻优并确定目标分配方案。在改进的蜂群算法中跟随蜂采用双向轮盘赌的方式选择引领蜂,既增加了种群多样性,又降低了算法陷入局部最优的概率。将改进蜂群算法用于求解雷达网监测多目标的分配方案,为解决雷达网监测多目标问题提供了一种新的方法。由仿真实验可以看出,该方法获得了较为理想的结果,求解效率进一步提高,求解结果更加稳定的优点。进一步研究表明,算法参数设置对改进蜂群算法得到的最优结果影响较大,如何找到算法中的最优参数以得到适应度更高的目标分配方案将是下一步的研究方向。
[1]陈轩,黄心汉.基于免疫遗传算法的雷达组网方法[J].计算技术与自动化,2014,33(2):89-92.
[2]连鲁军,吴士琦.基于混合蛙跳算法的雷达组网优化部署研究[J].浙江树人大学学报,2013,13(3):10-13.
[3]田德伟,何广军,尤晓亮,等.基于萤火虫算法的雷达目标分配方法[J].监视与控制学报,2015,37(2):62-65.
[4]刘伟,华中和.用遗传算法实现雷达网目标分配[J].情报指挥控制系统与仿真技术,2004,26(5):48-53.
[5]贾斌,肖兵,金宏斌.改进遗传算法在雷达网目标分配中的应用[J].计算机技术与自动化,2008,27(4):80-83.
[6]班祥东.蜂群算法理论研究综述[J].软件导刊,2012,11(10):36-38.
[7]罗文涛,许蕴山,肖冰松,等.预警探测中的多传感器多目标分配[J].电光与控制,2014,21(11):29-32.
[8]杨秀珍,鞠传文,何友.基于效能函数的传感器管理系统仿真[J].系统仿真学报,2003,15(2):251-261.
[9]KARABOGA D.An idea based on honey bee swarm for numerical optimization,Technical Report-TR06 [R].Erciyes University,2005.
[10]BONABEAUE,DORIGO MTHERAULAZG.Swarm intelligence:fromnature to artificial system[M].New York:Oxford University Press,1999:40-58.
[11]苏晓勤,孙鹤旭,潘旭华.改进蜂群算法的旅行商问题仿真[J].计算机工程与设计,2013,34(4):1421-1424.
[12]胡中华,赵敏.基于人工蜂群算法的TSP仿真[J].北京理工大学学报,2009,29(11):978-982.
[13]易正俊,韩晓晶.增强寻优能力的改进人工蜂群算法[J].数据采集与处理,2013,18(6):761-769.

