基于改进灰色聚类的装备器材库存分类方法*

吴龙涛，王铁宁，朱 域

（陆军装甲兵学院，北京 100072）

0 引言

库存分类是实施差异化库存管理、提高库存效益和保障效率的前提。随着装备的发展和高新技术的应用，装备器材库存种类急剧增加，而管理人员精力有限，难以同时精确地管理所有器材。因此，亟需一种有效的库存分类方法，对需要重点管理或只需一般管理的器材进行分类。

库存管理领域应用最广泛的分类方法是基于Pareto法则的ABC分类法［1］，按照年消耗额的高低将库存物品分为3类，分别选取严格或宽松的管理策略。但实际中影响库存管理的因素还有很多，如库存成本、提前期等，在库存分类时同样需要考虑。针对多指标库存分类问题，多数方法选择线性加权规划法［2］，利用德尔菲法［3］、层次分析法［4］、智能算法［5］等方法确定各指标的权重，然后对加权求和的综合评分排序，依据Pareto准则进行分类。但库存分类更倾向于一种模糊的不确定性问题，许多学者针对这一特点运用数据挖掘的思维，使用BP神经网络［1］、粗糙集［6］、贝叶斯网络［7］等方法从训练样本中寻找分类规律，但训练样本的容量和质量很难保证。

灰色聚类［8］是指按若干聚类指标将一个聚类群体归纳为几个灰类，与库存分类的过程十分相似，因此，非常适合用来解决库存分类问题。但传统的灰色聚类方法根据白化权函数的临界值计算指标的权重，若指标间量纲不同，权重的设置将没有意义［9］；而且聚类的白化权函数也要针对库存分类具体问题进行确定。因此，本文引入信息熵［10］和基于中心点三角白化权函数［11］，提出了装备器材库存分类中灰色聚类的权重和白化权函数设置方案。通过算例分析表明，本文提出的装备器材库存分类方法合理可行。

1 装备器材库存分类指标

库存分类研究中选取的库存分类指标通常包括年消耗额、提前期、库存成本、关键性、稀缺性、易损性等。文献［1，5-6］将构成年消耗额的单价和年消耗量单独作为两个指标，但这样容易出现不同器材间取值单位不一致、无法衡量的问题，如/kg和/m；而其中关键性等主观性较强的指标则不易量化。因此，从中选取年消耗额、库存成本、提前期作为装备器材库存分类指标。

此外，与企业稳定的生产活动相比，装备器材的消耗受时间、地域、人员等诸多不确定性因素的影响，使得需求量的波动较大。根据常用的确定装备器材库存量的公式（s为库存数量，μ和σ为间隔期需求量的均值和标准差，k为安全库存系数）可以看出，需求量的波动程度也是库存管理的一个重要决策因素。但直接以标准差衡量需求波动程度显然是不合适的，如标准差同为5、需求量均值分别为10和50的物品，前者需求波动程度更大。因此，定义需求波动系数作为装备器材库存分类的指标之一。

定义1 设订货间隔期内某器材需求量的均值为μ，标准差为σ，则该器材订货间隔期内的需求波动系数。

2 基于灰色聚类的装备器材库存分类方法

2.1 灰色聚类

灰色理论把只知道大概范围而不知道具体值的数称为灰数。例如，一件器材价值5 000元是一个白数，但器材很重要就是灰数。灰色聚类就是把若干对象归纳为几个聚类灰数（简称“灰类”）的过程。

由定义可知，聚类系数反映了聚类对象与灰类之间的隶属度，聚类对象与某个灰类的聚类系数越大，则属于该灰类的可能性越大。进而，如果聚类对象与某个灰类的聚类系数大于与其他灰类的聚类系数，则认为聚类对象属于该灰类，这就是聚类系数最大化原则［9］。

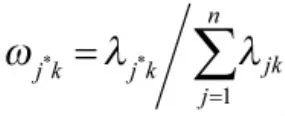
2.2 聚类指标的信息熵和熵权

熵［10］是热力学中表示分子状态混乱程度的一个状态参量，Shannon在信息论中最早提出了信息熵的概念和计算表达式，一组数据的信息熵越小，其中包含的信息量越大；反之，信息熵越大，信息量越小。下面通过定义给出信息熵在灰色聚类中设置聚类指标权重时的应用。

2.3 基于中心点三角白化权函数

白化权函数实现了灰色聚类由定性分析到定量研究的转化，是灰色聚类解决模糊评价问题的关键。但基本的灰色聚类方法中，并未对白化权函数的设定进行具体阐述，因而在应用灰色聚类时需要自行确定白化权函数。刘思峰等提出的基于端点三角白化权函数［14］和基于中心点三角白化权函数［11］被广泛应用，前者适用于各灰类边界明确、中心点不明确的情况，而后者则适用于中心点明确、各灰类边界不明确的情况。

中心点可以是区间的中点、中位数或均值，根据数列或指标的实际情况而定。基于中心点三角白化权函数的确定方法如图1所示，除首尾两个灰类外，各灰类的白化权函数是由本灰类和相邻两个灰类的中心点决定的。其中，灰类1的白化权函数称为下限测度白化权函数，记为；灰类s的白化权函数称为上限测度白化权函数，记为；灰类的白化权函数称为中测度白化权函数，记为。

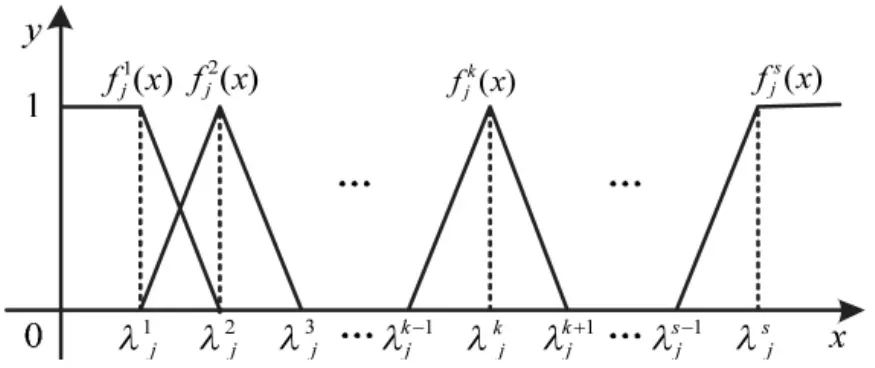
图1 基于中心点三角白化权函数设定

由图1可得，各灰类关于指标j的白化权函数表达式为

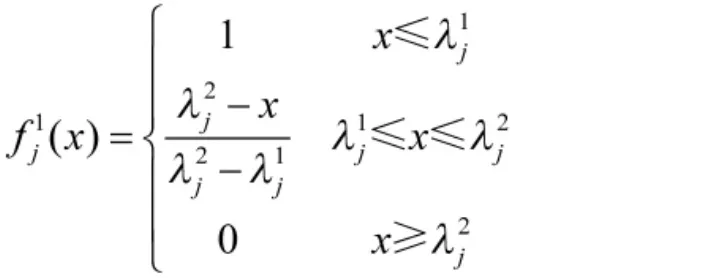
2.4 方法描述

综上所述，基于灰色聚类的装备器材库存分类方法的基本过程如下：

（1）给出所有器材关于各分类指标（年耗额、库存成本、提前期、需求波动系数）的无量纲化分类样本矩阵Xm×4；

（3）由样本矩阵Xm×4根据定义4计算各分类指标的熵权ωj；

（4）由 Xm×4、和ωj根据定义2计算每项器材关于库存分类k的聚类系数σki，进而得到聚类向量；

3 算例分析

S仓库是我军某一战术级装甲器材仓库，为了提高库存管理效率，下面使用本文提出的库存分类方法把S仓库的器材按管理重要程度分为“一般C、重要B、关键A”3类。随机抽取S仓库中50项器材，对近5年的请领、入库、出库等数据进行统计，得到如下页表1所示的分类样本矩阵X＝（xij）50×4（受篇幅限制，表1只给出了其中部分数据）。以器材1为例，库存分类过程如下：

（1）对样本矩阵各列进行无量纲化处理，可以使用均值化、极值化、区间值化等处理方法，经过测试对分类结果无显著影响。这里采用极大值化，器材1的分类数据处理后为。

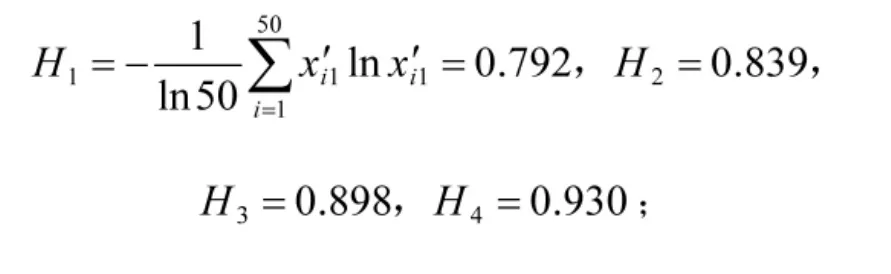
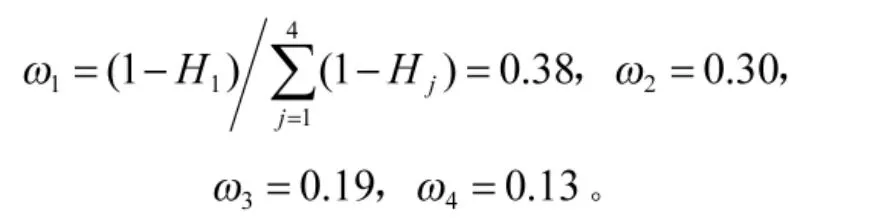
（3）根据Pareto法则原理，依次将各指标样本值降序排列，分别取前20%、次30%和后50%作库存分类边界，根据数据分布特征选择区间的中位数作为库存分类的中心点，得到如下矩阵

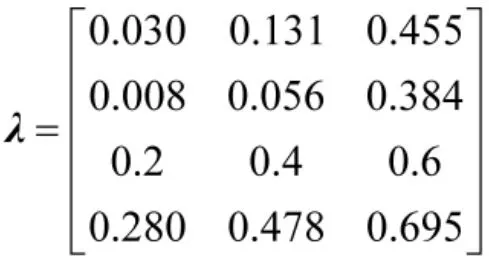
则各库存分类的白化权函数为

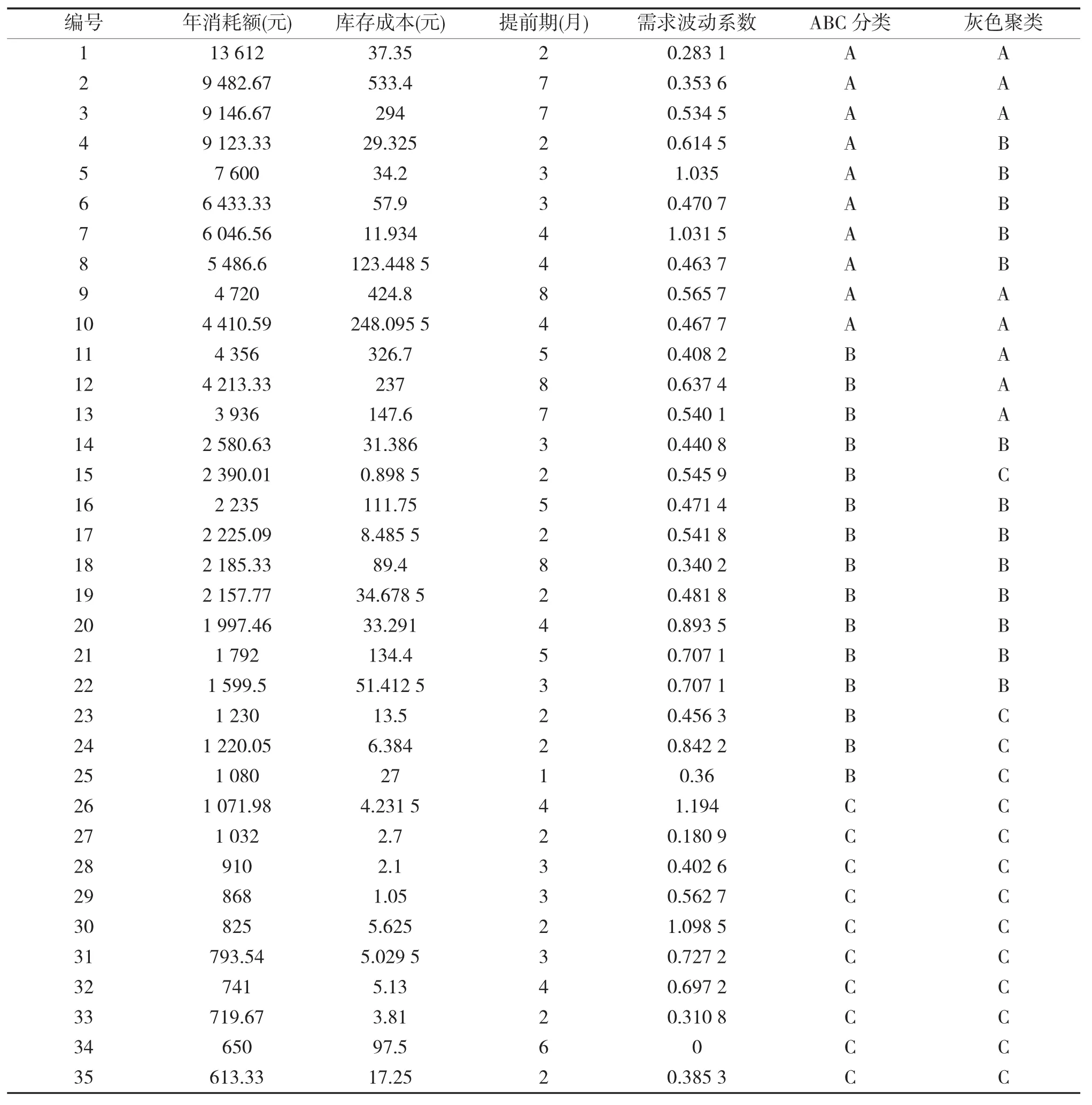
表1 装备器材库存分类数据及结果对比

将本文的库存分类方法编程，对50项器材分别使用经典ABC分类法和本文基于灰色聚类的库存分类法进行分类，结果如表1。使用两种方法器材分类整体分布对比如图2所示。从表1具体分类结果来看，器材4虽然年消耗额较高，但库存成本较低，提前期较短，所以被聚类为B类，类似的还有5～8、15、23～25 等；而器材 11～13 虽然年消耗额并不突出，但其他3项指标相对比较突出，因此，被聚类为A类。算例表明本文提出的库存分类方法是合理有效的，而且更加综合全面。

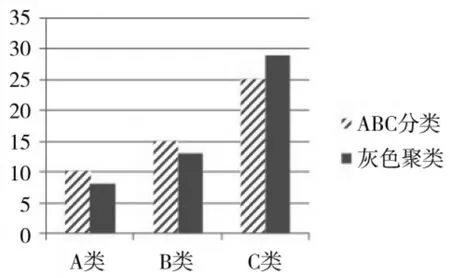
图2 两种方法器材分类整体分布

4 结论

装备器材种类的多样化增加了库存管理的难度。为此，本文设计了基于改进灰色聚类的装备器材多指标库存分类方法。同经典ABC分类方法相比，本文的分类方法考虑得因素更加综合全面；分类指标权重由库存器材具体情况客观决定，避免了权重确定的主观性；同时，本方法的计算过程易于程序实现，便于实际中的应用推广。

［1］PARTOVI F Y，ANANDARAJAN M.Classifying inventory using an artificial neural network approach ［J］.Computers and Industrial Engineering，2002（41）：389-404.

［2］PARK J，BAE H，BAE J.Cross-evaluation-based weighted linear optimization for multi-criteria ABC inventory classification ［J］.Computers and Industrial Engineering，2014，76（1）：40-48.

［3］杨学强，李文俊，岳勇.综合评价指标权重确定方法［J］.装甲兵工程学院学报，2015，29（1）：101-105.

［4］LOLLI F，ISHIZAKA A，GAMBERINI R.New AHP-based approaches for multi-criteria inventory classification［J］.International Journal of Production Economics，2014（156）：62-74.

［5］TSAI C Y，YEH S W.A multiple objective particle swarm optimization approach for inventory classification ［J］.International Journal of Production Economics，2008（114）：656-666.

［6］李波，赵志彦，段铁英.一种多准则库存分类的混合预测方法［J］.计算机集成制造系统，2004，10（5）：594-599.

［7］SUCAR L E，BIELZA C，MORALES E F，et al.Multi-label classification with Bayesian network-based chain classifiers［J］.Pattern Recognition Letters，2014（41）：14-22.

［8］刘思峰，谢乃明.灰色系统理论及其应用［M］.6版.北京：科学出版社，2013.

［9］董奋义，刘俊娟，刘斌，等.灰色综合聚类法的改进及其在河南省农村经济发展水平评价中的应用［J］.农业系统科学与综合研究，2010，26（4）：478-483.

［10］王东海，赵秋红.ABC库存分类的多指标体系及其信息熵方法［J］.数学的实践与认识，2014，44（13）：1-9.

［11］刘思峰，方志耕，杨英杰.两阶段灰色综合测度决策模型与三角白化权函数的改进［J］.控制与决策，2014，29（7）：1232-1238.

［12］张明媛，高颖，袁永博.模糊聚类和灰色聚类的集成分析方法［J］.模糊系统与数学，2015，29（3）：145-153.

［13］强凤娇.灰色聚类决策中指标权重和综合决策测度权系数的确定［J］.统计与决策，2015（22）：50-54.

［14］刘思峰，谢乃明.基于改进三角白化权函数的灰评估新方法［J］.系统工程学报，2011，26（2）：244-250.