并行广义本征值求解器GenELPA*

沈 瑜，孙广中

1.中国科学技术大学 超级计算中心，合肥 230026

2.中国科学技术大学 计算机科学与技术学院，合肥 230026

1 前言

在很多需要数值计算的领域，如何高效求解大型矩阵的本征值和本征向量是常见的问题。例如在电子结构理论中，人们常常要把求解的Kohn-Sham方程转换为矩阵形式，然后求出本征值[1]。很多时候系统需要通过多次自洽迭代达到稳态，而在每次迭代中都需要求解该方程，尤其在几百个原子以上的较大尺度下，该方程的求解成为最耗费时间的步骤[2]，因此如何求解Kohn-Sham方程成为影响计算速度的关键因素之一。

一般情况下，Kohn-Sham方程是一个广义本征值方程，具有如下形式：

其中，A和B为已知的N×N的矩阵；c是N×N的本征向量矩阵；λ是以本征值为对角元的矩阵。很多情况下，A和B都是对称矩阵（如果为实数矩阵）或者厄米矩阵（如果为复数矩阵），同时B还是正定且非奇异矩阵。这种情况下，可以把广义本征值方程转化为一般本征值方程，然后进行求解。

本征值的求解是数值计算的一个基本问题，直接对所有本征值和本征向量进行代数求解的计算复杂度为O(N3)，在需求解矩阵规模增长时，所需要的计算能力增长得非常快。但如果问题有一定特殊性，例如只需要一小部分本征值和本征向量，或者本征函数有一些约束条件等，可以采用迭代等方法来降低计算复杂度[3]。在某些情况下，甚至可以绕过求解本征值的步骤，从而使得问题复杂度降低到O(N)[4]。另一方面，也可以采用大规模并行的方法来加速本征值的计算。尤其是近些年超级计算机的飞速发展，不仅顶级超级计算机的规模迅速扩大，而且千核乃至万核级服务器也日趋普及（http://www.top500.org）。目前，有很多工作是研究大规模并行本征值求解，例如ScaLAPACK（scalable linear algebra package）[5]、PLAPACK（parallel linear algebra package）[6-7]、eigen_s和eigen_sx[8]、Elemental[9]、EleMRRR[10]等。同时，基于众核的 PLASMA（parallel linear algebra for scalable multicore architectures）和基于GPU的MAGMA（matrix algebra for GPU and multicore architectures）也随着近年来异构计算的发展而开发出来[11-14]。

2011年德国马克斯普朗克学会的科学家们为了解决在FHI-aims全电子结构软件中的针对上千个原子体系中需要求解的大规模对称和厄米矩阵的本征值问题，发展了面向P级应用的本征值求解库（eigenvalue solver for petaflop-applications，ELPA）[15]。ELPA具有相对传统ScaLAPACK更好的计算速度和并行效率，除了在FHI-aims[16]里得了应用，也为很多专业软件采用，例如针对纳米尺度材料模拟软件OpenMX（open source package for material explorer）[17]、量子化学和固体物理软件CP2K[18]等。

本文将介绍一种自行开发的基于ELPA的广义本征值求解器GenELPA，该求解器以开源形式公开发布（https://git.ustclug.org/yshen/GenELPA_C），它实现了转换广义本征值方程为一般本征值方程的方法，然后调用ELPA进行计算。为了方便使用，采用了类似ScaLAPACK的接口和自动选择最佳转化的方法，并提供了转化和求解分步调用的函数。本文将该求解器应用到由中国科学技术大学量子信息重点实验室开发的第一性原理软件ABACUS[19]（atomic-orbital based ab-initio computation at USTC，http://abacus.ustc.edu.cn）中，获得了理想的效果。

2 原理

求解广义本征值问题可以先将广义本征值方程转化为一般本征值方程，然后求解转化后的一般本征值问题。第一种转化方法是将B矩阵做Cholesky分解为上三角矩阵或者下三角矩阵，这里以上三角矩阵为例：

其中，U为上三角矩阵；UT是它的转置矩阵。

然后令：

那么方程（1）就变为标准本征值问题：

方程（5）可以通过ELPA来求解，如果需要本征向量的话，可以通过下式求得：

第二种方法是将B对角化后，求得B-1/2。即先用ELPA求解关于B的本征值方程，得到本征值和本征向量e={ei,i=1,2,…}和q={qij,i,j=1,2,…},然后有：

其中，B-1/2ij为矩阵B-1/2的矩阵元；qik和qkj为本征向量矩阵q的矩阵元；ek为第k个本征值。令：

则方程（1）可转变为一般本征值形式：

同样，上式可以通过ELPA来求解，如果需要本征向量的话，可以通过下式求得：

3 功能与使用

GenELPA主要功能是自动进行上述过程，用户只需要输入矩阵A和B以及进程的相关信息，就可以直接调用GenELPA进行计算。用户可自行选择转化方法以及是否计算本征向量。

在实际的电子结构计算中，有时候在进行迭代计算时，B矩阵保持不变而A矩阵会随着迭代的进行而不断更新，因此有必要将B矩阵的分解和求解最终结果分开，以避免重复计算。在GenELPA中，对这两步计算可以单独调用函数进行计算：第一步将B矩阵做Cholesky分解为上三角矩阵U,然后计算U-1,或者将B矩阵对角化后计算B-1/2；第二步再利用分解后得到的U-1或者B-1/2和A矩阵计算本征值和本征向量（如果需要的话）。

在第一步中，由于ELPA提供的Cholesky分解函数在某些较小的系统下可能会不稳定（https://doxygen.cp2k.org/d9/d87/classcp_fm_diag.html#a89cb3ce325957a111071b0d2200bbf17），还提供了使用Sca-LAPACK中的分解函数作为替代选择。因此加上对矩阵B进行对角化的方法，总共有3种方法对矩阵B进行分解。在GenELPA中，使用者可以指定使用某种方法，也可以由程序自动选择。

GenELPA中的函数采用类似ScaLAPACK的命名规则：第一个字母如果是p，表明是个并行的函数；第二个字母表示处理的数据类型，d为双精度实数，z为双精度复数。ELPA本身也有两个求解引擎“ELPA1”和“ELPA2”，因此需要调用ELPA的函数也有两个不同的版本，分别对应“ELPA1”和“ELPA2”，其函数名分别用1和2结尾区别。

表1是目前GenELPA提供的函数。GenELPA的输入参数类似于ScaLAPACK，此外还加入了在整个程序中只需要一次初始化的一些参数，以避免重复计算。本文以pdSolveGenEigen1为例说明输入参数。

其中，各个参数意义详见表2。

使用GenELPA时，有以下需要说明的地方：

（1）ELPA底层为FORTRAN语言编写，因此二维数组（a、b、q、work）中的数据在内存中的存储需要按FORTRAN语言使用的列主序方式存储。至于进程矩阵，则不限定采用行主序或者列主序。

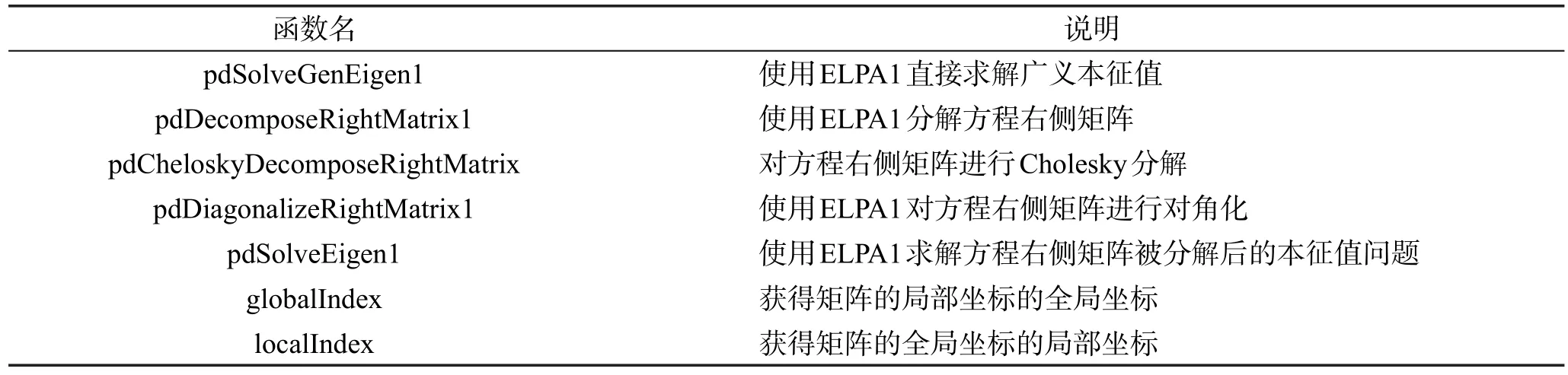
Table 1 Function list of GenELPA表1GenELPA函数列表

Table 2 Parameter list of pdSolveGenEigen1表2 pdSolveGenEigen1参数列表

（2）程序运行中，数组a、b会被用作中间变量，因此程序结束后，变量a、b的值会被改变。如果希望保留输入数组，请事先将输入数组复制一份。

（3）除非必要，否则method方法最好选择0作为默认参数。当使用参数0时，在程序结束后method会返回实际使用的方法序号。

（4）程序目前尚在开发中，会尽快采用ELPA2进行计算和处理复数方程的部分补齐，同时会进一步对性能调试优化。

4 性能测试

本文使用了20 000×20 000大小的矩阵进行了实际测试，测量了不同方法所需要的矩阵分解时间、本征值计算时间和总计算时间。使用的测试平台是中国科学技术大学超级计算中心的TC4600集群[20]，该集群的每个计算节点有24个CPU核心，因此测试使用的CPU核心数为24的整数倍，即48、96、192、384和768个。

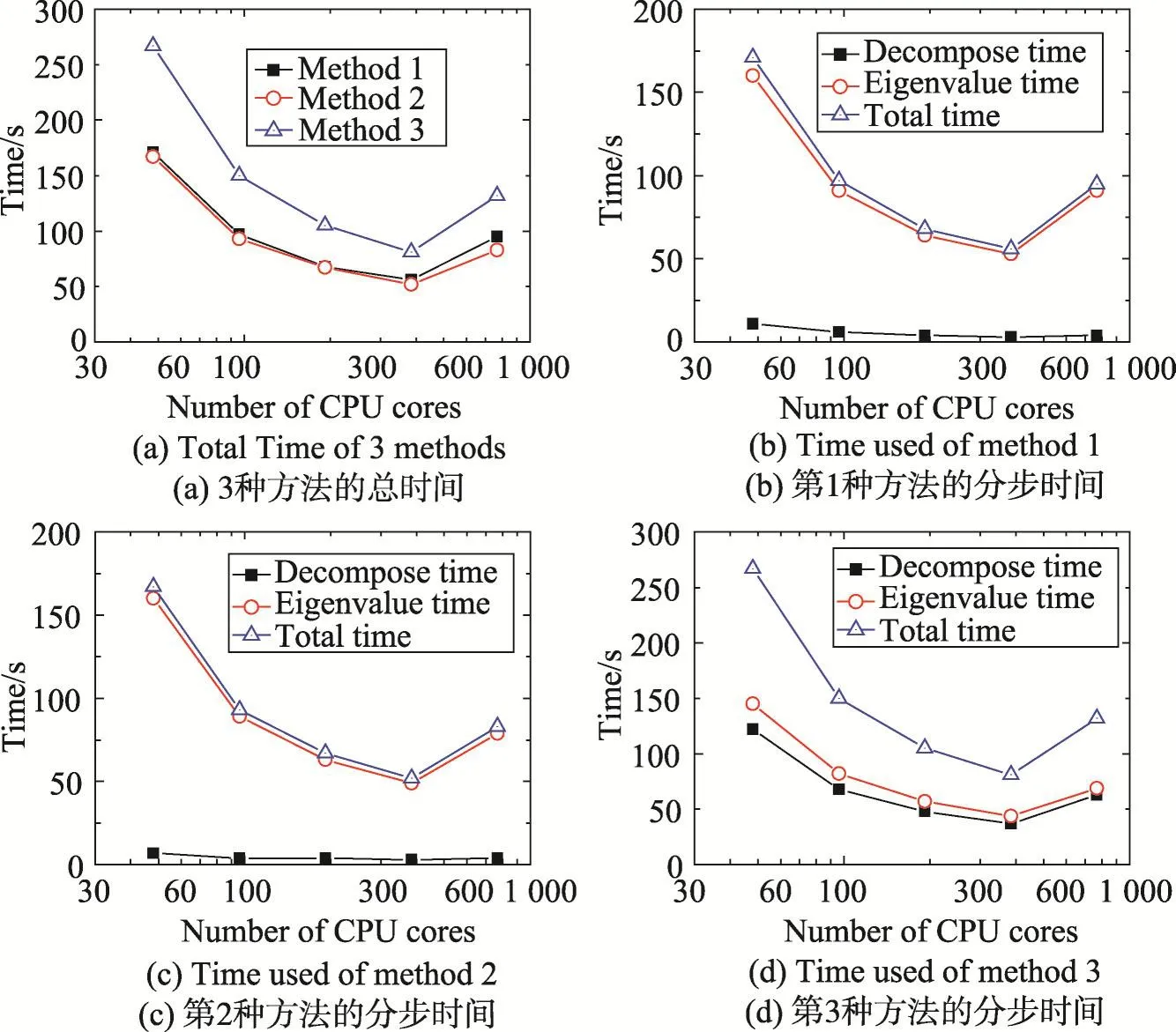
Fig.1 Time to calculate all eigenvalues图1 计算所有本征值的时间

Fig.2 Time to calculate half of all eigenvalues图2 计算一半本征值的时间

图1和图2分别是计算全部（20 000）和一半（10 000）本征值的时间统计，横轴为使用的CPU核心数，纵轴为时间。其中图（a）是3种方法所用整体时间的对比，黑色方块线为方法1，红色圆圈线为方法2，绿色三角线为方法3。可以看出在使用CPU核心数较少时方法1和方法2的速度几乎一样，而使用CPU核心数较多时，方法2要稍快一些。至于方法3，所需时间一直要比其他两种方法长很多。图（b）～（d）分别是方法1到方法3的分步骤时间统计，其中黑色方块线为右侧矩阵分解时间，红色圆圈线为计算本征值时间，绿色三角线为总时间。由于方法3通过对角化右侧矩阵进行分解时需要计算右侧矩阵的本征值，方法3的矩阵分解时间要接近计算本征值的时间。而方法1和方法2的矩阵分解使用Cholesky方法，所需时间要远远小于计算本征值的时间。

测试结果表明：首先，使用Cholesky分解比对角化能够更快地将矩阵B分解；其次，在使用CPU核心数较少时，采用ScaLAPACK和ELPA提供的Cholesky分解方法耗时几乎一样。

需要说明的是，该测试程序还没有得到充分优化，因此在大规模并行效率上还不如ELPA本身的效率，后续工作中将进一步对其优化。

将此求解器应用到第一性原理软件ABACUS，并使用一个由2 048个硅原子（Si）组成的晶体进行了初步测试（图3），该体系在每一个电子步的迭代中需要计算一次26 000×26 000大小的广义本征值方程。同样在TC4600系统中，采用96个CPU核心进行了测试。作为对比，ABACUS原始使用的求解器是由中科院网络信息中心开发的HPSEPS（high performance symmetric eigenproblem software）软件包[21]。测试结果表明，采用GenELPA进行计算后，本征值求解部分计算时间由4 300 s减少到2 000 s，程序整体运行时间由4 800 s减少到2 500 s，程序性能取得了显著提高，如图4所示。

Fig.3 Asample containing 2 048 silicon atoms图3 包含2 048个硅原子的测试算例

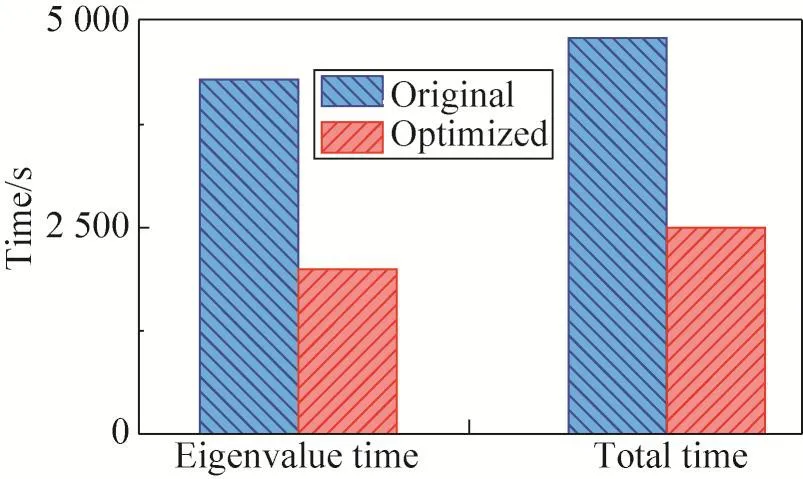
Fig.4 Comparison of computing time图4 计算时间对比

5 总结

本文基于具有良好的计算速度和并行效率的本征值求解器ELPA编写了广义本征值求解器GenELPA，该求解器为用户提供了3种将广义本征值问题转化为一般本征值问题的方法，简化了使用方式，避免了在求解某些问题时ELPA中可能存在的问题；实际测试表明该求解器还具有较好的计算速度和并行效率。针对电子结构计算等需要大规模并行求解广义本征值的问题，能够有效地简化难度，提高效率。

致谢本工作得到了中国科学技术大学中科院量子信息重点实验室的何力新教授、任新国教授和刘晓辉博士在应用集成和实例测试中的帮助。

[1]Martin R M.Electronic structure:basic theory and practical methods[M].New York:Cambridge University Press,2004.

[2]Li Pengfei,Liu Xiaohui,Chen Mohan,et al.Large-scale ab initio simulations based on systematically improvable atomic basis[J].Computational Materials Science,2016,112(44):503-517.

[3]Golub G H,van der Vorst H A.Eigenvalue computation in the 20th century[J].Journal of Computational and Applied Mathematics,2000,123(1):35-65.

[4]Goedecker S.Linear scaling electronic structure methods[J].Reviews of Modern Physics,1999,71(4):1085-1123.

[5]Blackford L S,Choi J,Cleary A,et al.ScaLAPACK users'guide[M].Philadelphia:SIAM,1997.

[6]Alpatov P,Baker G,Edwards C,et al.PLAPACK:parallel linear algebra package design overview[C]//Proceedings of the 1997 ACM/IEEE Conference on Supercomputing,San Jose,Nov 15-21,1997.New York:ACM,1997:1-16.

[7]Baker G,Gunnels J,Morrow G,et al.PLAPACK:high performance through high-level abstraction[C]//Proceedings of the 1998 International Conference on Parallel Processing,Minneapolis,Aug 10-14,1998.Washington:IEEE Computer Society,1998:414-422.

[8]Imamura T,Yamada S,Machida M.Development of a highperformance eigensolver on a peta-scale next-generation supercomputer system[C]//Proceedings of the 2010 International Conference on Supercomputing in Nuclear Applications and Monte Carlo,Tokyo,Oct 17-21,2010.Tokyo:Atomic Energy Society of Japan,2011:643-650.

[9]Poulson J,Marker B,van de Geijn R A,et al.Elemental:a new framework for distributed memory dense matrix computations[J].ACM Transactions on Mathematical Software,2013,39(2):13.

[10]Petschow M,Peise E,Bientinesi P.High-performance solvers for dense hermitian eigenproblems[J].SIAM Journal on Scientific Computing,2013,35(1):C1-C22.

[11]Haidar A,Solcà R,Gates M,et al.Leading edge hybrid multi-GPU algorithms for generalized eigenproblems in electronic structure calculations[C]//LNCS 7905:Proceedings of the 28th International Supercomputing Conference,Leipzig,Jun 16-20,2013.Berlin,Heidelberg:Springer,2013:67-80.

[12]Agullo E,Demmel J,Dongarra J,et al.Numerical linear algebra on emerging architectures:the PLASMA and MAGMA projects[J].Journal of Physics:Conference Series,2009,180:012037.

[13]Dongarra J J,Tomov S.Matrix algebra for GPU and multicore architectures(MAGMA)for large petascale systems[R].Knoxville:University of Tennessee,2014.

[14]Buttari A,Dongarra J,Kurzak J,et al.The impact of multicore on math software[C]//LNCS 4699:Proceedings of the 8th International Workshop on Applied Parallel Computing:State of the Art in Scientific Computing,Umeå,Jun 18-21,2006.Berlin,Heidelberg:Springer,2007:1-10.

[15]Marek A,Blum V,Johanni R,et al.The ELPA library:scalable parallel eigenvalue solutions for electronic structure theory and computational science[J].Journal of Physics:Condensed Matter,2014,26(21):213201.

[16]Blum V,Gehrke R,Hanke F,et al.Ab initio molecular simulations with numeric atom-centered orbitals[J].Computer Physics Communications,2009,180(11):2175-2196.

[17]Ozaki T.Variationally optimized atomic orbitals for largescale electronic structures[J].Physical Review B,2003,67(15):155108.

[18]Hutter J,Iannuzzi M,Schiffmann F,et al.CP2K:atomistic simulations of condensed matter systems[J].Wiley Interdisciplinary Reviews:Computational Molecular Science,2014,4(1):15-25.

[19]Liu Xiaohui,Chen Mohan,Li Pengfei,et al.Introduction to first-principles simulation package ABACUS based on systematically improvable atomic orbitals[J].Acta Physica Sinica,2015,64(18):187104.

[20]Li Huimin.User manual of Sugon TC4600 100TFLOPS supercomputing system[EB/OL].(2016-06-15).http://scc.ustc.edu.cn/zlsc/tc4600/tc4600-userguide.pdf.

[21]Zhao Yonghua,Chi Xuebin,Wang Wu.HPSEPS software and parallel computing performance on thousand cores[J].e-Sciense Technology&Application,2010,1(4):20-28.

附中文参考文献:

[19]刘晓辉,陈默涵,李鹏飞，等.基于数值原子轨道基组的第一性原理计算软件ABACUS[J].物理学报,2015,64(18):187104.

[20]李会民.曙光TC4600百万亿次超级计算系统使用指南[EB/OL].(2016-06-15).http://scc.ustc.edu.cn/zlsc/tc4600/tc4600-userguide.pdf.

[21]赵永华,迟学斌,王武.HPSEPS软件包及其在千核上的并行计算性能[J].科研信息化技术与应用,2010,1(4):20-28.