社交关系在基于模型社会化推荐系统中的影响*

房倩琦，柳 玲，文俊浩，曾 骏，高 旻

重庆大学 软件学院，重庆 401331

1 引言

推荐系统常用于解决互联网上的信息过载问题，传统推荐系统基于协同过滤的方法[1-2]进行推荐。然而在真实场景中，大多数用户只对很少的项目进行了评分，缺乏共同的历史评分数据将造成协同过滤方法的推荐质量明显下降。现今，由于社交平台的流行，社交关系信息获取更为便捷，而社交信息的融入能够明显缓解传统推荐系统中的评分数据稀疏和冷启动问题[3]，因此社会化推荐系统[4-5]应运而生。

与传统的推荐系统有所不同，社会化推荐系统在进行推荐时，不仅考虑用户的历史评分信息，同时也考虑了用户的社交关系信息，因而在一些场景中取得了更好的推荐结果。根据系统算法的不同原理，社会化推荐系统中采用的推荐算法可以分为基于内存的推荐算法和基于模型的推荐算法。由于后者通常能够方便地融合先验知识，目前社会化推荐系统方面的研究者将主要的研究方向集中于构建性能更优的基于模型的推荐算法[4]。现有的基于模型的方法的一般思路为从完整的已有评分矩阵（关系矩阵）上提取用户与项目的潜在特征，然后通过将两个低维特征矩阵相乘来对缺失评分进行预测。由此思路衍生出的一系列模型算法在实验数据集上取得了较高的推荐性能，并被广泛应用于实际系统[6]。然而，由于分解得到的低维隐式特征通常难以解释，并且社交关系作为算法输入的一个重要部分，其密度信息与结构信息的改变可能会使推荐性能产生较大差异，故社交关系在基于模型的推荐系统中的影响仍待探索。

本文着力于研究基于模型的社会化推荐系统中社交关系变化对推荐结果的影响，并主要从以下方面进行了实验探究：（1）社会化推荐系统中关系数量的变化对推荐结果的影响；（2）关系数量的变化对不同用户组的影响；（3）社交网络中心节点与边的变化对推荐结果的影响。实验结果表明，社交关系的数量增多将对推荐质量带来明显提升，对获取新用户偏好的帮助尤为明显，同时中心节点对推荐质量的影响具有决定性作用。

2 相关工作

社会化推荐系统的输入信息由两部分信息构成：用户评分信息与社交关系信息。现有的大部分社会化推荐系统选用协同过滤模型作为基础模型构建系统，并将社交信息作为社会化推荐系统输入信息的一部分。因此，基于协同过滤的社会化推荐系统的框架[7]包含两部分：基础协同过滤模型和社会化信息模型。

根据协同过滤基础模型的不同，可将社会化推荐系统分为两类，基于内存的推荐系统和基于模型的推荐系统。前者使用经典的协同过滤模型作为基础模型，考虑了用户的社会关系。通常，该类社会化推荐系统首先找出当前用户的关联用户集合，然后再从中获取评分来对当前用户的缺失评分进行预测，不同的系统采取了不同的获取N+i的方式。Social based Weight Mean算法[8]中，对于给定用户ui，将与给定用户有直接关系的用户作为给定用户的关系数据集N+(i)。Golbeck[9]提出的 TidalTrust算法中为了得到更多的关联用户，考虑了用户间的信任传播，且认为：（1）传播路径越短，信任值越大；（2）信任值高的路径产生的预测结果越准确。Jamali等人[10]提出的TrustWalker与TidalTrust类似，但采用了随机游走的思路来寻找更多关联用户，并加入了相似项目的概念，使得预测结果更为精确。

不同于传统的推荐系统中使用的矩阵分解算法，基于模型的社会化推荐系统将社交关系信息引入到算法输入中。矩阵分解[11]是一种最为主流的基于模型的基础算法，该算法通过已有的评分信息对高维评分矩阵进行低秩逼近，分解得到两个低维特征矩阵，并利用分解后的矩阵乘积来对缺失评分进行预测。它的通用最优化目标函数[12]可以表示为：

其中，R∈Rm×n为用户对商品的评分矩阵；T∈Rm×m为用户与用户之间的社交关系矩阵；U∈Rk×m为用户潜在特征矩阵；V∈Rk×n为项目潜在特征矩阵；Social(T,S,Ω)是对社交网络分析所得的社会化信息；Ω是从社会化信息中学习得到的参数；系数α用于控制Social(T,S,Ω)的影响。根据对Social(T,S,Ω)定义的不同，基于模型的社会推荐系统被进一步划分为3个类别：协同分解方法（co-factorization methods）、集成方法（ensemble methods）以及正则化方法（regularization methods）。

2.1 协同分解方法

协同分解方法的原理为社交信息和评分信息可以通过共享用户潜在特征空间来进行连接。即是说，社交信息中的用户潜在特征空间与评分矩阵中用户潜在特征空间重合。由此可以导出公式R=UTV,T=UTZ,其中Z∈Rk×m是信任隐式特征。SoRec（social recommendation）[13]是这类算法中最具代表性的一个。

SoRec算法的最优化目标函数可以表示为：

其中，Social(T,S,Ω)定义为

2.2 集成方法

集成方法假设用户的偏好是由用户个人的口味和其好友的口味共同决定。评分矩阵中的缺失评分可以通过将用户的评分和其好友的评分做线性组合预测而产生。这类算法中最具代表性的算法就是RSTE（recommend with social trust ensemble）[14]算法。

RSTE中预测评分的线性表达式Ri,j表示为：

其中，Ni是用户所有朋友的集合；Si,k是用户i所有朋友评分之和的正则化项；β用来控制用户朋友评分在结果中所占的比例，其最优化目标函数可以表示为：

其中，Social(T,S,Ω)定义为βSUTV),tr()表示矩阵的迹。

2.3 正则化方法

正则化方法假定用户的偏好会近似于其好友，因此在模型训练过程中，正则化方法会使用户的潜在特征向量接近其好友的潜在特征向量。SocialMF（matrix factorization based model for recommendation in social rating networks）[15]是这类方法中最典型的一种。

在 SocialMF 算法中，Social(T,S,Ω)被定义为用户i的偏好应接近于用户i所有好友的平均偏好。

SocialMF旨在优化以下问题：

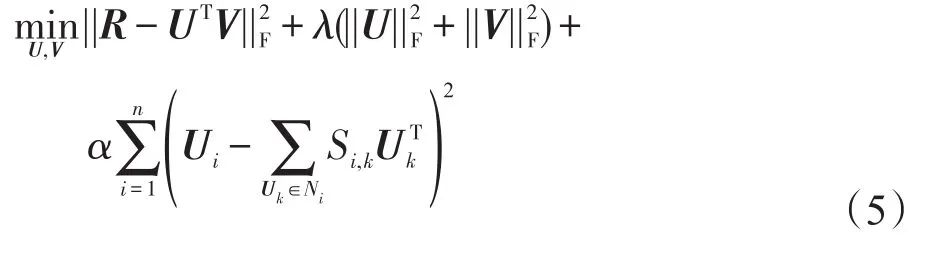
3 社交关系对基于模型的社会化推荐系统影响的实验设计

本章通过实验探究了基于模型的社会化推荐系统中关系的变化对推荐性能的影响，主要实验内容如下：（1）关系数量的变化对用户推荐性能的影响；（2）关系数量的变化对不同用户组推荐性能的影响；（3）中心节点与边的变化对推荐性能的影响。

3.1 实验数据

实验中使用的数据集为从Epinions网站爬取的包含评分信息和社交信息的真实数据集[6]。从中随机抽取了1 500名用户和其信任用户，并保留了这些用户之间所有的信任关系与商品评分。采样数据包含8 183个用户，104 000个项目和339 000个评分。用户信任关系数为20 000。评分尺度为1至5，喜好程度依次递进。信任关系为二元信任：存在信任关系，值为1；不存在信任关系，值为0。图1给出了数据集的相关信息统计。

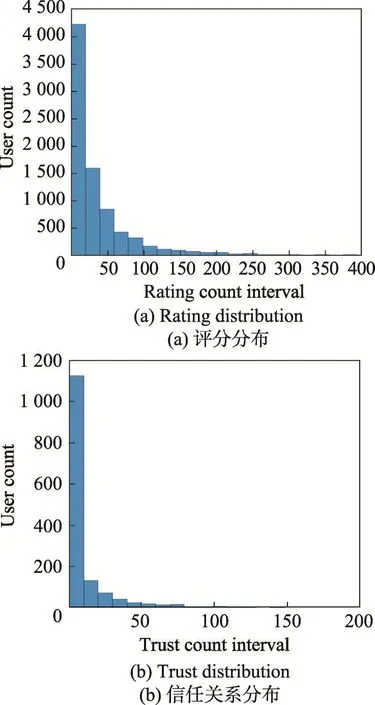
Fig.1 Rating distribution and trust distribution图1 数据集的评分分布与信任关系分布

3.2 评价指标

本文基于评分角度选取均方根误差（root mean squared error，RMSE）作为评价指标，基于项目排序角度选取准确率、召回率、F1值作为评价指标。这几个指标均为最常用的推荐质量度量方法。

RMSE值越小，表明预测精度越高。计算公式如下：

其中，ri,j是真实评分；rˆi,j是预测评分；N为数据数量。

准确率和召回率取值在0和1之间，数值越接近1，推荐精度越高。准确率的定义为：

F1值是准确率与召回率的调和平均值，其值越大，推荐精度越高。F1值可表示为：

其中，P为准确率；R为召回率。

3.3 实验设计

实验探索了社交关系对基于2.1节提到的3种模型算法的社会化推荐系统的影响。3种算法的参数都被设置为通过实验寻找到的最佳值，算法实现平台为开源的推荐系统项目LibRec[16]。实验采用了十折交叉验证，实验设备为配备i7 4790k Intel处理器，8 GB内存的PC机。实验分为以下三部分进行。

3.3.1 关系数量的变化对推荐性能的影响

此部分实验采用按比例随机移除用户关系的方法，依次删减用户信任关系数据集中所有关系数量的10%、30%、50%、70%、90%，查看关系稀疏程度对推荐精度的影响。

3.3.2 关系数量变化对不同用户推荐性能的影响

此部分探究关系数量的变化对不同用户的影响，在进行实验之前，首先需要按照一定的标准对用户类别进行划分。将评分数量大于等于50的用户划为活跃用户组（active），评分数量大于等于10小于50的用户划为普通用户组（general），评分数量小于10的用户划为不活跃用户（inactive）。此部分的实验仍然采用第一部分实验对用户数量的处理方法，查看不同关系数量下不同用户推荐性能的变化。

3.3.3 中心节点与边的变化对推荐性能的影响

此部分选择了社交网络的3个中心特性来探究其变化对推荐性能的影响。3个中心特性为度中心性、点介数中心性、边介数中心性[17]。

度中心性是在社交网络分析中刻画节点中心性（centrality）的最直接度量指标。一个节点的度（degree）（在图论中，某节点的邻接节点的数量成为该节点的度）越大，该节点在网络中就越重要。节点的度

中心性可以用公式表示：

其中，n表示节点vi所属网络中节点的总数量。度中心性的值与节点vi的度成比例。

介数表示一个网络中经过该节点（边）的最短路径的数量。在一个网络中，节点（边）的介数越大，它在节点的通信中起到的作用越大。介数中心性又可分为点介数中心性和边介数中心性，其直接定义式为：

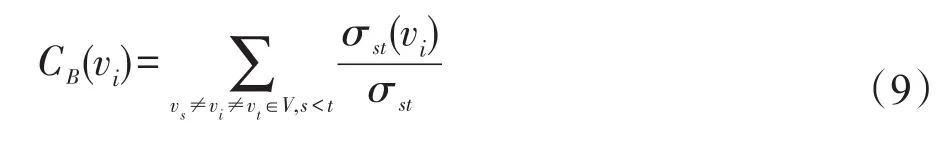
其中，σst(vi)表示经过节点vi（边）的s→t的最短路径条数。直观上来说，介数反映了节点vi（边）作为“桥梁”的重要程度。

度中心性代表点的关系重要程度，按照度中心性由高到低对用户信任关系数据进行排序后，分别按照5%、10%、15%、20%、25%删减数据后得到5次实验的用户信任关系数据集。点介数中心性代表点在社交网络通信中点的重要程度，按照点介数中心性由高到低对用户信任关系数据进行排序后，分别按照1%、2%、3%、4%、5%删减数据后得到此部分5次实验的用户信任关系数据集。边介数中心性代表边在通信中的重要程度，将边介数排序后按照10%、30%、50%、70%、90%的比例删减数据得到实验所用数据集。

4 实验结果与分析

4.1 关系数量的变化对推荐性能的影响

按照3.3.1小节实验设计进行实验后得出结果中RMSE值如表1所示，准确率、召回率、F1值如图2所示。

分析实验结果可知，随着关系数量的减少，推荐结果的准确率、召回率和F1值整体呈现下降的趋势。RMSE值呈现波动微小或不规律的趋势。但考虑到实际情况中，用户只关注推荐列表中的结果，故认为准确率、召回率和F1值的变化较RMSE更具价值和参考性。从项目排序的指标看，3种模型算法中RSTE算法的推荐性能下降幅度尤为明显。推测原因为RSTE算法的评分结果是由用户本身评分与其好友评分线性组合而得，故其受关系影响最为直接与明显，且在随机移除10%与30%的关系后，RSTE的推荐质量并无明显下降，认为这是由于删减的关系中存在部分噪声，删减后对结果影响不大。SoRec算法受关系变化影响相对较弱，但整体的推荐性能也细微地呈现出下降趋势。推测这是由于在SoRec算法中，关系矩阵采用了协同分解的方式，语义上更难以解释，故朋友的影响相对RSTE较间接与隐式。而SocialMF尽管有较低的RMSE，其准确率和召回率却很低，且几乎没有波动，故认为其整体上基本不受关系数量变化的影响。

4.2 关系数量变化对不同用户推荐性能的影响

按照3.3.2小节实验设计进行实验后得出结果中RMSE值如表2所示，准确率、召回率、F1值如图3所示。

分析实验结果可知，在SoRec与RSTE算法中，随着关系的减少，3种用户的准确率、召回率和F1值都呈下降趋势，但通过对比可知，活跃用户的准确率和F1值受关系影响最大，下降趋势最明显，普通用户次之，不活跃用户的准确率和F1值下降的趋势最微弱，受关系影响最小，但其召回率下降最剧烈，受关系影响最大。推测活跃用户之所以对更多项目进行了评分，原因之一可能为活跃用户更多地关注了其朋友喜好的项目，浏览并评分了该项目。故当关系数量减少时，该用户组的准确率下降最为明显。而不活跃用户由于评分数量较少，推荐列表中较小的变动，也会造成召回率的较大变化，故其召回率变化最为明显。普通用户则介于两者之间。

4.3 中心节点与边的变化对推荐性能的影响

按照3.3.3小节实验设计进行实验后得出结果中RMSE值如表3所示，准确率、召回率、F1值如图4所示。

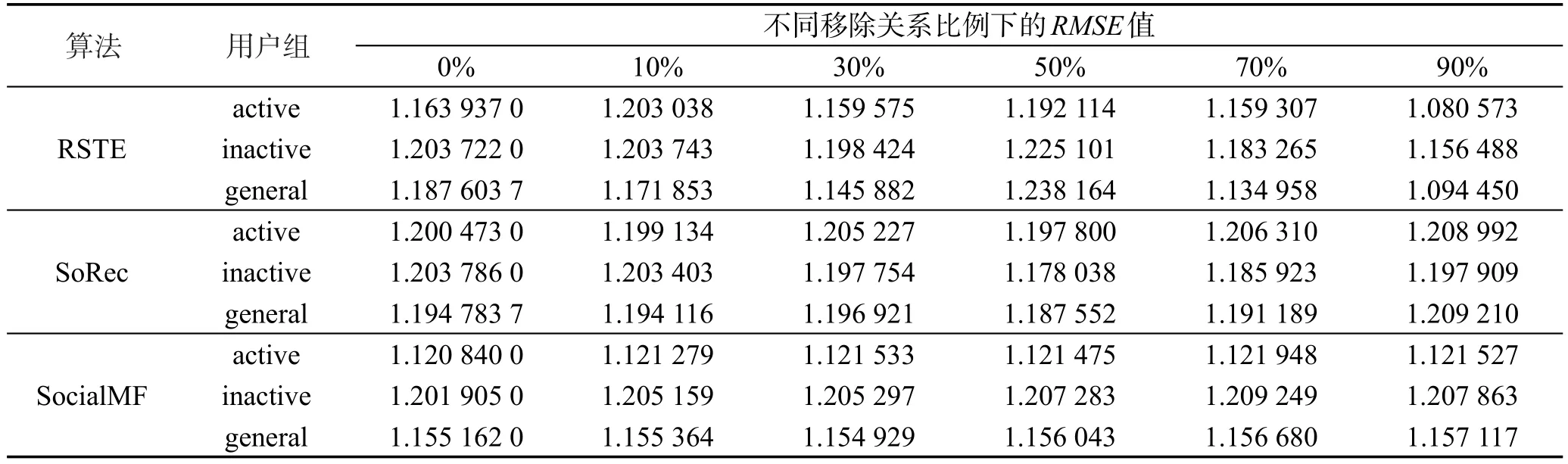
Table 2 RMSE of 3 algorithms on different user groups with different relation density表2 社交网络中用户数量的变化时，不同用户组推荐结果的RMSE值

Table 3 RMSE of 3 algorithms on condition that central nodes are removed proportionally表3 按中心性进行节点关系删减之后3种算法的RMSE值

Fig.3 Precision,recall and F1 of 3 algorithms on different user groups with different relation density图3 不同用户组在3种算法下的准确率、召回率和F1值

从表3中可看出，3种算法的RMSE值在度中心性与点介数实验中均产生了一定变化，其中RSTE算法随着中心节点/边的移除，RMSE值减小，而SoRec算法的RMSE值表现为增大，SocialMF的RMSE值也有微小增大。另外3个指标的变化如图4所示，RSTE算法在度中心性与点介数中心性实验部分，推荐结果的准确率、召回率与F1值呈陡峭下降后趋于平缓的态势，因关键点在所有数据中所占比重较小，在第一次删减时，关键点的减少对算法的影响较大。而在关键边实验中，推荐结果的准确率、召回率与F1值呈现明显的逐步下降的趋势，且从度中心性和介数中心性实验的图像可以看出，在删减中心性排序靠前的10%的节点后，曲线呈现小幅度上升趋势，推测这是由于所删数据中包含一定噪声而造成的。而其他两个算法中，SoRec算法受其影响较弱，而SocialMF依然几乎不受影响。

4.4 中心节点的重要性验证

由4.3节发现，中心节点在推荐算法中发挥着尤为重要的作用。因此在本节中将节点的度中心性信息融入到社会化推荐模型中，对以上实验结论进行进一步验证。

Fig.4 Precision,recall and F1 of 3 algorithms on conditions that nodes are removed proportionally by different ways图4 按不同方式删减数据后3种算法的准确率、召回率和F1值

融入节点度中心性的RSTE+算法的优化函数为：

融入节点度中心性的SocialMF+算法的优化函数为：

融入节点度中心性的SoRec+算法的优化函数为：

其中，Wi为Ui所代表的节点的中心性权重，满足公式：

Wi∈(1,2),centrality∈[1,n],n为该网络中最大中心性值。若Ui为孤立节点，则Wi=1。

在对相同的数据集进行实验后，得出结果如表4所示。从表4中可以看出，将中心性信息融入算法后，3种推荐算法的推荐质量均有不同程度的提升。

Table 4 MAE and RMSE of algorithms after adding importance information of nodes表4 增加节点重要性信息后算法的MAE值与RMSE值

通过以上实验可以发现，尽管在不同算法中社交信息的结合方式不同，但社交关系的加入明显改善了推荐质量。同时，更多的关系信息将使得推荐结果更为精确，对于新用户的推荐，关系的增多带来的性能提升尤为显著。此外，社交关系的结构也左右着推荐质量，中心节点在推荐算法中发挥着尤为重要的作用。

5 结束语

社交网络平台的兴起带来了丰富的社会信息，若将这些社会信息合理利用，社会化推荐系统的推荐质量将得到极大改善。

本文着力于研究基于模型的社会化推荐系统中社交关系变化对推荐结果的影响，并主要从以下方面进行了实验探究。首先，对社交网络中关系数量的变化对推荐性能的影响进行了分析；其次，通过对用户进行分类，分别研究关系数量的变化对不同用户推荐性能的影响；最后，探究了在按照不同社交网络特性使关系数量发生变化时对推荐性能的影响，并对结果进行了验证。实验发现高密度的关系信息的融入将使得推荐结果更为精确，对于新用户的推荐性能提升尤为明显，社交信息数据中的噪声会对推荐精度产生负面影响。此外，中心节点在推荐算法中发挥着尤为重要的作用。

在之后的工作中，将继续在社交网络对推荐质量的影响方面开展研究工作。根据本次的实验结果，寻找有效去除社交信息数据噪声的新方法，探索能提高推荐质量的最佳的社交信息结合方式，并使用更多具有代表性的算法与数据集进行实验。

[1]Schafer J B,Frankowski D,Herlocker J,et al.Collaborative filtering recommender systems[M]//LNCS 4321:The Adaptive Web.Berlin,Heidelberg:Springer,2007:291-324.

[2]Su Xiaoyuan,Khoshgoftaar T M.A survey of collaborative filtering techniques[J].Advances in Artificial Intelligence,2009(12):4.

[3]Gao Huiji,Tang Jiliang,Liu Huan.gSCorr:modeling geosocial correlations for new check-ins on location-based social networks[C]//Proceedings of the 21st International Conference on Information and Knowledge Management,Maui,Oct 29-Nov 2,2012.New York:ACM,2012:1582-1586.

[4]Meng Xiangwu,Liu Shudong,Zhang Yujie,et al.Research on social recommender systems[J].Journal of Software,2015,26(6):1356-1372.

[5]Zhu Yangyong,Sun Jing.Recommender system:up to now[J].Journal of Frontiers of Computer Science and Technology,2015,9(5):513-525.

[6]Chen B C,Guo Jian,Tseng B L,et al.User reputation in a comment rating environment[C]//Proceedings of the 17th International Conference on Knowledge Discovery and Data Mining,San Diego,Aug 21-24,2011.New York:ACM,2011:159-167.

[7]Guy I.Social recommender systems[M]//Ricci F,Rokach L,Shapira B,ed.Recommender Systems Handbook.Boston:Springer US,2015:511-543.

[8]Victor P,Cornelis C,Cock M D,et al.A comparative analysis of trust-enhanced recommenders for controversial items[C]//Proceedings of the 3rd International Conference on Weblogs and Social Media,San Jose,May 17-20,2009.Menlo Park:AAAI,2009:342-345.

[9]Golbeck J.Generating predictive movie recommendations from trust in social networks[C]//LNCS 3986:Proceedings of the 4th International Conference on Trust Management,Pisa,May 16-19,2006.Berlin,Heidelberg:Springer,2006:93-104.

[10]Jamali M,Ester M.TrustWalker:a random walk model for combining trust-based and item-based recommendation[C]//Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Paris,Jun 28-Jul 1,2009.New York:ACM,2009:397-406.

[11]Symeonidis P.Matrix and tensor factorization with recommender system applications[J].Graph-Based Social Media Analysis,2016,39:187.

[12]Tang Jiliang,Hu Xia,Liu Huan.Social recommendation:a review[J].Social Network Analysis and Mining,2013,3(4):1113-1133.

[13]Ma Hao,Yang Haixuan,Lyu M R,et al.SoRec:social recom-mendation using probabilistic matrix factorization[C]//Proceedings of the 17th ACM Conference on Information and Knowledge Management,Napa Valley,Oct 26-30,2008.New York:ACM,2008:931-940.

[14]Ma Hao,King I,Lyu M R.Learning to recommend with social trust ensemble[C]//Proceedings of the 32ndAnnual International ACM SIGIR Conference on Research and Development in Information Retrieval,Boston,Jul19-23,2009.New York:ACM,2009:203-210.

[15]Jamali M,Ester M.A matrix factorization technique with trust propagation for recommender in social networks[C]//Proceedings of the 4th ACM Conference on Recommender Systems,Barcelona,Sep 26-30,2010.New York:ACM,2010:135-142.

[16]Guo Guibing,Zhang Jie,Sun Zhu,et al.LibRec:a Java library for recommender systems[C]//CEUR Workshop Proceedings 1388:Proceedings of the 23rd Conference on User Modeling,Adaptation,and Personalization,Dublin,Jun 29-Jul 3,2015.

[17]Wang Haoxiang,Zeng Shan,Liu Huiyang.An importance analytical approach for online social network[J].Journal of Shanghai Jiaotong University,2013,47(7):1055-1059.

附中文参考文献：

[4]孟祥武,刘树栋,张玉洁,等.社会化推荐系统研究[J].软件学报,2015,26(6):1356-1372.

[5]朱扬勇,孙婧.推荐系统研究进展[J].计算机科学与探索,2015,9(5):513-525.

[17]王昊翔,曾珊,刘挥扬.虚拟社交网络中节点重要度分析[J].上海交通大学学报,2013,47(7):1055-1059.