改进的ICP算法在三维模型配准中的研究*

杨 军，张 瑶，黄 亮

1.兰州交通大学 电子与信息工程学院，兰州 730070

2.兰州交通大学 自动化与电气工程学院，兰州 730070

1 引言

配准技术是当今数字化检测领域的一项关键技术，最早出现于医疗诊断和图像处理领域[1]，目前已广泛应用于逆向工程[2]、虚拟现实[3]、机器人[4]和柔性装配[5]等领域。

模型配准是指通过在源模型和目标模型之间构造一个三维空间变换，使源模型在此变换作用下能够最大限度地和目标模型重合。目前主要有三类方法：第一类是基于标记的配准方法，通过确定两模型中对应的特征点，并由对应特征点计算目标模型和源模型之间的空间变换。该方法主要应用于医学领域。第二类是基于表面的配准方法，在模型表面上定义并计算突出的特征，根据模型表面的共同特征在重叠区域内搜索两个表面之间的唯一匹配模式。该方法通常应用于工业领域的模型配准。第三类是基于体素相似性的配准方法，不需要对像素做预处理（去噪或者分割），直接作用于图像，但该方法计算量太大，很少用于三维模型配准。模型配准一般分为两步：初始配准和精确配准。初始配准是通过缩小两模型旋转和位移误差将两模型大致调整到同一位置，为迭代最近点（iterative closest point，ICP）配准提供最优初始值；精确配准则是利用初始匹配值不断地执行迭代变换，并使迭代收敛到全局最优的配准结果。

1992年，Besl和Mckay提出了ICP算法[6]，由于其操作简单和良好的配准效果而广泛应用于各种领域的配准问题，然而ICP算法对于初始值的敏感性极高且运行效率低。针对经典ICP算法的缺点，中外许多学者对寻找和选取对应点对设计了各种算法，以保证能够得到最优的初始匹配点对，提高ICP算法的速度和精确度。文献[7]结合点集增强技术与经典ICP算法，将一些新的采样点加入到已有的点集中并作为标记点，用于解决由多传感器扫描获取的三维点云数据的坐标融合问题，提高了配准的准确度和鲁棒性，然而该算法太依赖新加入的标记点，而标记点对应位置准确与否直接影响配准结果。文献[8]利用模型表面曲率变化和法线矢量之间的夹角来约束对应点对，这种方法虽然提高了配准效率和准确度，但仍然需要用户给定初始配准点。文献[9]除了用模型表面一点和其邻近点组成的切平面与此点处法向量的夹角阈值约束对应点对外，还加入了点云数据的对应点对间的欧氏距离阈值来选取最合适的对应点对，这种方法对于小型零件检测效果很好，但当点云数据规模超过8 000点之后，其精确度不如经典ICP算法。文献[10]认为错误的对应点对对配准结果影响较大，于是将图像信息融合到改进的ICP算法中，用SIFT特征点减少错误对应点对，提高了配准的准确度和效率，但此方法除了必须的点云外还需要模型在真实环境中的二维图像信息。文献[11]提出了基于点云边界特征点的改进ICP算法。首先，对点云最小包围盒进行三维空间划分，运用边界种子网格识别及生长算法，从点云边界提取特征点，运用奇异值矩阵分解法求出点云的变换矩阵，得到初始配准结果。其次，对点云对应点赋予权重，剔除权重大于阈值的点，通过对目标函数引入M-估计，剔除异常点。最后，在初始配准的基础上，运用改进的ICP方法精确配准。算法效率提高了，但准确度并不是很高。

常用的初始配准方法有重心重合法[12]、标签法[13]、提取特征法[14-15]。重心重合法计算出两模型的重心坐标，然后将重心重合，这种方法只能缩小平移错位而无法缩小旋转错位；标签法在测量时人为地贴上一些特征点，然后利用这些特征点进行定位，根据这些对应的特征点将两模型大致调整到同一位置，这种方式仍然是依赖于测量和仪器的；提取特征法，如提取平面特征、轮廓曲线等，通过将模型表面特征相同部分重合以达到初始配准的目的，但这种方式要求点云有比较明显的突出特征。

本文针对ICP算法对于初始值的敏感性以及整体与部分模型的配准精确度两方面进行了改进。首先，采用主成分分析法（principal component analysis，PCA）对模型进行初始配准，使用三维缩放变换将两模型调整为同等大小。然后，用KD-tree进行最近点搜索提高搜索速度。由于本文主要针对整体与部分模型间的配准，对配准精度要求更高，故利用自适应最优阈值优化ICP算法，提高模型配准的准确度。最后，为了防止在上下或前后颠倒的情况下进行三维模型重合度检测，做最后的反转调整。

2 模型的初始配准

在运用ICP算法对模型进行精确配准之前，两模型的点集有可能在不同的坐标系下，也有可能处于同一坐标系的任意位置，那么点集的迭代初始值就不能满足精确配准的要求，因此需要通过搜索最近点，或者使用三维几何特征来计算两组点集的匹配条件。然而，算法的复杂度和计算量会剧增，影响执行效率。因此，在精确配准前先进行两模型点集间的初始配准，为精确配准提供初始值以提高最终的配准精确度和效率。

文中使用了一种全局配准方法。由于两模型点集的主轴形状相似度很高，可以通过计算两组点集的主轴以得到点集之间的刚体变换矩阵，此方法称为主成分分析法。给定一组点集P={P1,P2,…,Pn},计算其均值和协方差矩阵cov,对矩阵cov进行特征向量分解，得到的正交特征向量作为点集P的三坐标轴X、Y、Z,以均值为坐标系原点，建立这组点集的坐标系。可以用同样的方式处理源模型和目标模型的点集，并将两模型的坐标系进行位置调整，以满足初始配准的要求。

然而，本文并没有将两模型新的坐标系调整至同一位置，而是先将两模型进行三维缩放调整为同等大小。

给定包含n个采样点的源模型S={s1,s2,…,sn}和包含m个采样点的目标模型T={t1,t2,…,tm},用矩阵（1）和（2）分别表示源模型和目标模型点云数据的坐标。其中，下标s和t分别表示源模型和目标模型。

分别计算源模型和目标模型的点集在X、Y、Z坐标轴上的平均值分别表示点在X轴、Y轴、Z轴上的坐标。

分别计算源模型和目标模型所有点坐标值xi、yi、zi和相应均值之间的差值，如式（5）和（6）所示。

用Bs和Bt分别表示经过PCA分析后形成的新坐标系下源模型和目标模型各点的新的坐标矩阵。

分别计算源模型和目标模型每一列的最大值和最 小 值 max(Bs)、 min(Bs)、 max(Bt)、 min(Bt),并 计 算最大值和最小值之间的差值Ds、Dt。

构造新的矩阵D,其中元素d是矩阵Ds和Dt对应元素相除得到的一行三列矩阵，d(1,1)、d(1,2)、d(1,3)分别表示矩阵d的第一行一列、一行二列和一行三列元素。

D即为源模型到目标模型的缩放矩阵，因此模型的缩放调整由下式完成：

再将源模型依次绕X轴、Y轴、Z轴、XOY面、XOZ面、YOZ面反转并求出每次反转后的误差，选取误差最小的反转方式来调整源模型的方向。这样做既节省时间又不影响结果。

3 模型的精确配准

初始配准只是将源模型和目标模型缩放至同等大小，并调整至方向基本一致，其精度太低，远不能达到完全配准的要求。为了提高配准精度，还需在初始配准的基础上进行精确配准。本文采用ICP算法进行精确配准，其关键是对应点集配准（corresponding point set registration）。

对应点集配准算法的目的是利用最小二乘法计算模型间最优的坐标变换矩阵。对两个点集，可以采用单位四元数法[1]得到它们之间的变换矩阵。

用S和T分别表示源模型和目标模型的点云数据，它们应满足以下条件：

（1）T中有m个点和S中有n个点，且m=n;

（2）对于T中的任意点ti都对应于S中具有相同下标的si,即ti=(sisi、ti分别表示源模型和目标模型上的点）。

设旋转变换向量为单位四元数qrotat=[q0q1q2q3]T,其中q0≥0,并且,则可以得到3×3旋转变换矩阵R(qrotat)。设平移变换向量为qtrans=[q4q5q6]T,则求解对应点集间的最佳坐标变换向量问题可转化为求解qrotat和qtrans使得函数f(qtrans,qrotat)最小化的问题：

算法流程如下：

步骤1给定源模型和目标模型的对应点集S和T,计算目标模型点集T的重心μT和源模型点集S的重心μS:

步骤2由点集T和S构造协方差矩阵：

步骤3由协方差矩阵构造4×4对称矩阵：

其中，I3是 3×3单位矩阵；tr(ΣT,S)是矩阵 ΣT,S的迹，Δ=[A23A31A12]T,Ai,j是ΣT,S的反对称矩阵,Ai,j=(ΣT,S-ΣTT,S)i,j。

步骤4计算Q(ΣT,S)的特征值和特征向量，其最大特征值对应的特征向量即为最佳旋转向量qrotat=[q0q1q2q3]T,最佳旋转矩阵R(qrotat)为：

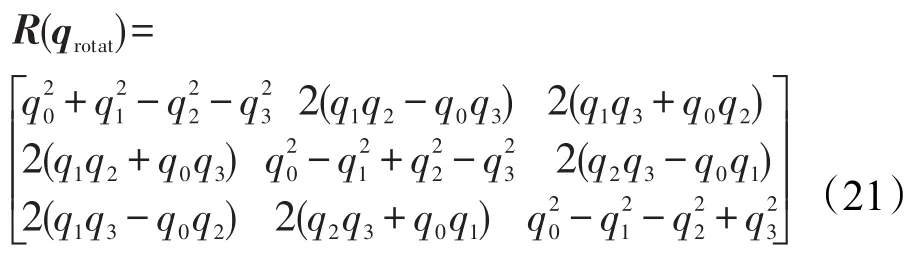
步骤5计算最佳平移向量为：

步骤6利用已得到的平移向量和旋转向量，计算dl=f(qtrans,qrotat),即迭代后的最小误差。

4 改进的ICP算法

ICP算法是目前应用最普遍的配准方法，其配准效果良好，但是算法本身计算效率不高。而KD-tree[12,16]是一种分割k维数据空间的数据结构，主要应用于多维空间关键数据的搜索（如本文中的最近邻搜索），并对搜索空间进行层次划分，具有搜索速度快的优点，故本文采用KD-tree搜索最近点来提高搜索效率。此外，整体与部分模型间的配准对于配准精度的要求更高，故本文采用自适应的最优阈值来优化迭代结果，提高了经典ICP算法的配准精度。

在两模型初始配准之后，不直接执行ICP算法，而是给定不同的阈值K，计算不同阈值时对两模型执行ICP算法所对应的配准误差，记录最小误差所对应的阈值并记为Kbest,用Kbest作为阈值，重新执行迭代最近点算法，直至算法收敛。

在执行ICP算法之后有可能会出现模型上下或者前后颠倒的现象，这是由于算法在执行过程中，可能会出现由于初始配准的不够准确导致执行ICP算法时不能找到正确的对应点对，故目前通常的做法是在初始配准后用最小包围盒的方法进行校正。但在实验中发现即使在初始配准后用最小包围盒进行矫正，最终还是可能会出现这种状况。

因此，本文算法在执行完ICP配准后，增加了三维目标重合度检测算法，根据两模型重合度再进行最后的反转调整，这里也要用到最小包围盒。根据包围盒立方体的三条边与三个坐标轴间的位置关系，包围盒分为沿坐标轴的轴向包围盒AABB（axisaligned bounding box）和有向包围盒OBB（oriented bounding box）[17]两种，如图1所示。本文选用OBB包围盒。

Fig.1 Axis-aligned bounding box(left)and oriented bounding box(right)图1 AABB包围盒（左）和OBB包围盒（右）

设Vs为源模型点云包围盒体积，Vt为目标模型点云包围盒体积，Vi为源模型点云和目标点云包围盒相交得到的包围盒的体积，则包围盒重合系数为：

如果τ＞thr,thr为设定阈值，则两点云模型大致重合。否则两模型不重合，那么反转坐标系的X轴或Y轴，将X轴和Y轴是否反转的4种情况全部测试完，并且没有任何一个τ大于thr,则说明两模型间差异较大，不能配准。

算法流程如图2所示，具体步骤说明如下。

步骤1输入源模型和目标模型的点云数据。

步骤2经过缩放，使两模型大小相同，再用矩阵C调整模型的方向。

步骤3用KD-tree来搜索目标模型最邻近点为对应点对，计算源模型上一点到目标模型上对应点之间距离的平均值aver和标准差sde。

步骤4设变量k,且1≤k≤3。k从1开始每隔0.05取一个值，得到不同的阈值K=k×aver+sde,对对应点对进行筛选，对应点对间的距离小于阈值的保留，否则剔除。计算得到不同阈值K执行ICP算法后对应的配准误差，记录最小误差对应的阈值为Kbest。

步骤5以Kbest为阈值执行ICP算法，并计算每次执行ICP算法后的配准误差。

步骤6判断误差是否收敛，若收敛，则两模型完成配准。若不收敛，判断迭代次数是否超出预设值，如超出，则强制结束迭代，两模型无法完全配准；如迭代次数没有超出预设值，返回步骤4。

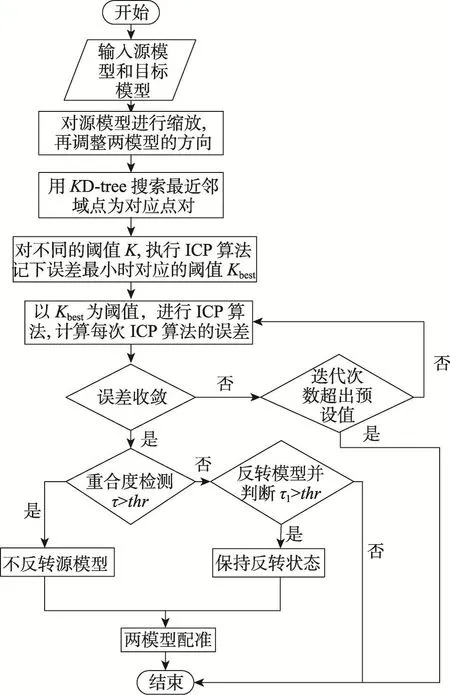
Fig.2 Flow chart of improved ICP algorithm图2 算法流程图

步骤7ICP算法结束后，执行三维目标重合度检测算法，分析两个目标的重合度情况，根据重合度再进行最后的旋转调整。

5 实验结果与分析

在基于极点谱植入的初始化过程中，由于优化策略采用了贪婪优化算法，从而建立了较好的初始对应关系。对已建立的初始对应关系再通过贪婪优化算法进行优化，就可得到最终的稀疏对应关系。

本文算法采用Matlab编程实现，实验中迭代次数预设最大值为300，针对部分模型（与源模型相比，目标模型缺少了某一部件）与完整模型进行实验，并将本文算法的误差与经典ICP算法进行对比。

图3是缺少两只小臂且没有穿衣服的人体模型（绿色）与完整模型（黄色）在只执行初始配准算法后的结果，可以看出配准精确度很差，没有对齐。同样的模型，图4所示实验表示只用精确配准的结果，配准效果依然不好。由此可见，如果没有初始配准为ICP算法计算出一个最优的初始值，则配准效果较差，这是由于ICP算法对初始值的敏感性所致。图5所示为本文算法的配准结果和迭代误差图，基本完全配准，最终配准误差为4.217×10-5。图6为缺少一条腿的马模型（绿色）和完整马模型（黄色）使用本文算法的配准结果和迭代误差。可以看出，在迭代过程的初期误差曲线有曲折，当迭代次数超过20次时，算法收敛，基本达到完全配准。最终配准误差为11.981×10-5。图7所示为缺少两只胳膊的人模型（绿色）与完整模型（黄色）的配准结果，此组模型中源模型（绿色）与目标模型（黄色）在小腿部分不完全相同，从配准结果看小腿部分绿色多而其他部分黄色多，在迭代过程中不断地前后调整导致误差不停波动，最终配准误差为14.139×10-5。图8为缺少一只胳膊且穿衣服的人体模型（绿色）与完整模型（黄色）使用本文算法的配准结果。与前三组模型相比，此模型的点云规模较大，且表面纹理复杂（因为衣服的皱褶）。可以看出，配准效果良好，但是在模型的脚腿部由于有衣服浮动的影响，两模型有差别，在迭代过程中不断地调整，最终配准误差在24.975×10-5附近波动收敛。当两模型姿态完全相同时，本文算法会完全配准，但当两模型姿态有所区别时，本文算法会在不同的部分不断调整迭代直到达到预设迭代值。

Fig.3 Result of using initial registration separately to align point clouds图3 仅用初始配准的结果

Fig.4 Result of using precise registration separately to align point clouds图4 仅用精确配准的结果

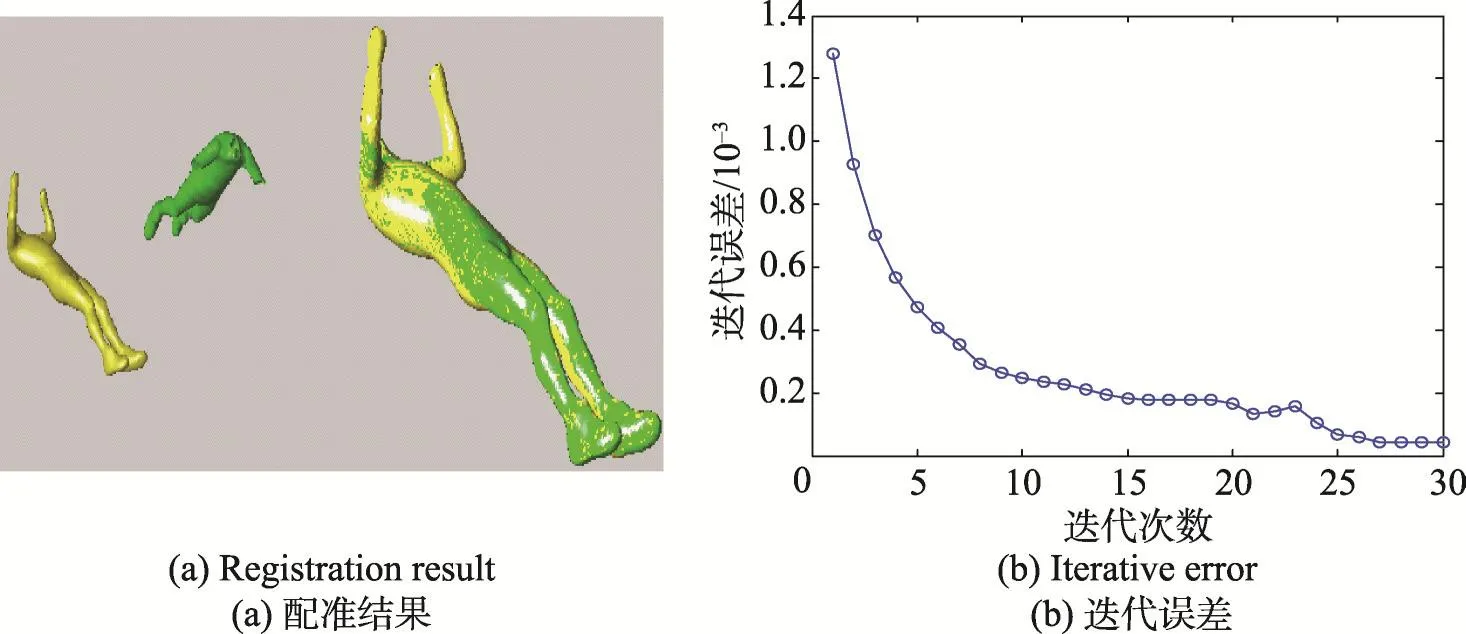
Fig.5 Registration result and iterative error of two human models(complete human model vs partial human model lack of two forearms)图5 完整与部分（缺少两只小臂）人体模型的配准结果与迭代误差

Fig.6 Registration result and iterative error of horse models(complete horse model vs partial horse model lack of right foreleg)图6 完整与部分（缺少一条腿）马模型的配准结果与迭代误差

Fig.7 Registration result and iterative error of human models(complete human model vs partial human model lack of two arms)图7 完整与部分（缺少两只胳膊）人体模型的配准

Fig.8 Registration result and iterative error of two human models with clothes(complete human model vs partial human model lack of right arm)图8 穿衣服的完整与部分（缺少右臂）人体模型配准与迭代误差

本文算法对完整模型之间的配准也非常有效。图9是4组完整模型的配准结果，可以看出，配准效果良好，骨头、猫、狗、人体模型的最终配准误差分别为10.224×10-5、0.380 42×10-5、2.569 8×10-5、6.842 4×10-5。

表1是本文算法和经典ICP算法对不同点云数目的模型进行配准的误差对比。本文算法根据每个模型的实际情况，搜索出最适合的阈值来筛选出最合适的对应点对，提高配准的准确度。且本文主要针对整体与部分模型间的配准，对配准精确度要求更高。可以看出，本文算法对于人和马模型（整体与部分模型）配准精确度的提高程度相对于猫和狗模型（两个完整模型）高很多。配准误差对比表明本文算法既能用于源模型是目标模型的某些部件这种情况，也适用于两个完整模型的配准，同时提高了经典ICP算法的模型配准精度。

Fig.9 Registration results of 4 sets of complete models图9 4组完整模型配准结果

6 结束语

随着科技工业的快速发展，医学和工业等领域对各种技术检测的精确度要求越来越高，模型配准是这些检测领域中的基本问题。本文提出了加入缩放功能的PCA算法，使用KD-tree搜索邻近点提高搜索速度，并使用自适应最优阈值优化ICP算法提高其准确度。此外，还进行模型重合度检测做最后调整避免出现模型上下或前后颠倒问题。实验结果表明本文算法既可以配准整体与部分模型，也适用于两个完整模型间的配准问题，同时提高了配准精度和效率。然而，在整体与部分模型的配准中，目标模型经常比源模型多一些部件，当搜索目标模型的所有点以寻找源模型的对应点时，往往也会搜索在源模型中没有对应点的部件。这属于无用遍历，增加了程序的运行时间，故在程序的运行速度方面可以再做进一步改善，比如利用三维网格分割技术，先将目标模型中多余的部件去除掉，然后再执行本文改进的ICP算法来进一步提高速度，这将是下一步的研究方向。

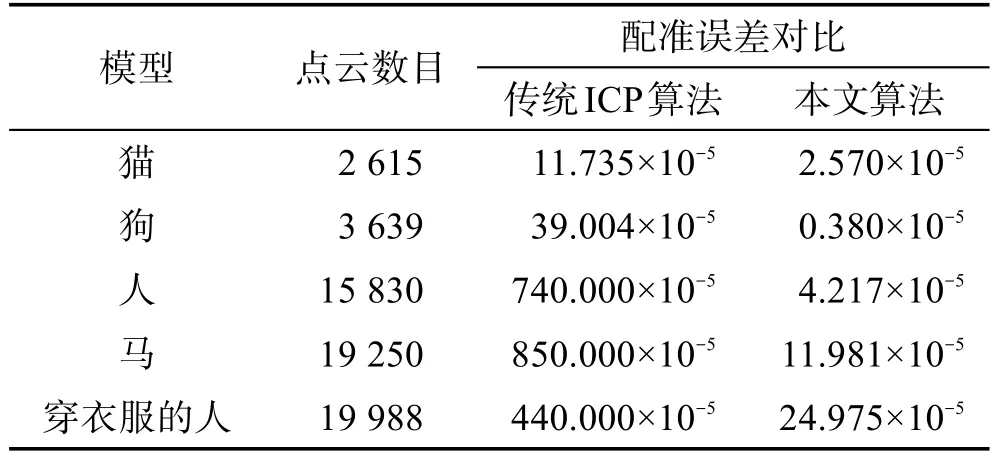
Table 1 Comparison of registration error between traditional ICP algorithm and improved ICP表1 本文算法与传统ICP算法配准误差对比

[1]Zhang J,Yan C H,Chui C K,et al.Multimodal image registration system for image-guided orthopaedic surgery[J].Machine Vision&Applications,2011,22(5):851-863.

[2]Imbert M,Li Xiaoxing.Automatic registration of 3D point clouds for reverse engineering[J].Journal of Computational&Theoretical Nanoscience,2011,4(6):2431-2432.

[3]Lemeszenski D D A,Nakamura R.A marker-free calibration and registration process for multiple depth maps from structured light sensors and its application in video avatar systems[C]//Proceedings of the 15th Symposium on Virtual and Augmented Reality,Cuiabá-Mato Grosso,May 28-31,2013.Washington:IEEE Computer Society,2013:73-82.

[4]Schneider C,Guerrero J,Nguan C,et al.Intra-operative“pick-up”ultrasound for robot assisted surgery with vessel extraction and registration:a feasibility study[C]//LNCS 6689:Proceedings of the 2nd International Conference on Information Processing in Computer-Assisted Interventions,Berlin,Jun 22,2011.Berlin,Heidelberg:Springer,2011:122-132.

[5]Jacobs A G,Jung B,Ober C K,et al.Control of PS-b-PMMA directed self-assembly registration by laser induced millisecond thermal annealing[C]//Proceeding of the SPIE 9049,Alternative Lithographic Technologies VI,Bellingham,Mar 28,2014.San Jose:SPIE,2014:4177-4180.

[6]Besl P J,Mckay N D.A method for registration of 3-D shapes[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1992,14(2):239-256.

[7]Senin N,Colosimo B M,Pacella M.Point set augmentation through fitting for enhanced ICP registration of point clouds in multisensor coordinate metrology[J].Robotics and Computer-Integrated Manufacturing,2013,29(1):39-52.

[8]Bae K H,Lichti D D.A method for automated registration of unorganized point clouds[J].ISPRS Journal of Photogrammetry and Remote Sensing,2008,63(1):36-54.

[9]Zhong Ying,Zhang Meng.Automatic registration of point clouds based on improved ICP algorithm[J].Control Engineering of China,2014,21(1):37-40.

[10]Zheng Zhongyang,Li Yan,Wang Jun.LiDAR point cloud registration based on improved ICP method and SIFT feature[C]//Proceedings of the 2015 International Conference on Progress in Informatics and Computing,Nanjing,Dec 18-20,2015.Washington:IEEE Computer Society,2015:588-592.

[11]Wang Xin,Zhang Mingming,Yu Xiao,et al.Point cloud data registration using improved iterative closest point method[J].Optics and Precision Engineering,2012,20(9):2068-2077.

[12]Liu Jiang,Zhang Xu,Zhu Jiwen.ICP three-dimensional point cloud registration based onK-D tree optimization[J].Engineering of Surveying and Mapping,2016,25(6):15-18.

[13]Meng Cai,Zhang Jun,Zhou Fugen,et al.New method for geometric calibration and distortion correction of conventional C-arm[J].Computers in Biology&Medicine,2014,52(3):49-56.

[14]He Bingwei,Lin Zeming,Li Y F.An automatic registration algorithm for the scattered point clouds based on the curvature feature[J].Optics&Laser Technology,2013,46(1):53-60.

[15]Lakehal A,Beqqali O E,Zemzami O A.Retrieval of similar shapes under affine transform using affine length paramete-rization[J].Journal of Computer Science,2010,6(10):1226-1232.

[16]Shakhnarovich G,Darrell T,Indyk P.Nearest-neighbors methods in learning and vision:theory and practice[J].Pattern Analysis andApplications,2008,11(2):221-222.

[17]Walizer L E,Peters J F.A bounding box search algorithm for DEM simulation[J].Computer Physics Communications,2011,182(2):281-288.

附中文参考文献：

[9]钟莹,张蒙.基于改进ICP算法的点云自动配准技术[J].控制工程,2014,21(1):37-40.

[11]王欣,张明明,于晓,等.应用改进迭代最近点方法的点云数据配准[J].光学精密工程,2012,20(9):2068-2077.

[12]刘江,张旭,朱继文.一种基于K-D树优化的ICP三维点云配准方法[J].测绘工程,2016,25(6):15-18.