考虑燃料成本的集装箱码头集卡路径优化

赵金楼， 黄金虎， 刘馨， 高宏玉

(1.哈尔滨工程大学 经济管理学院，黑龙江 哈尔滨 150001； 2.工业和信息化部电子第五研究所，广东 广州 510610)

在实现既定目标下，有效对资源进行调度优化近年来引起了学者们的重视。周林等[1]基于以物流成本和延迟惩罚成本之和为目标函数，构建了多任务集成调度模型，采用基于优先权的遗传算法，对多起始地-多目的地的多任务集成调度问题进行研究。Bookbinder等[2]通过构建概率模型来选择最大持有时间和期望的发货量，结合已有的卡车运输时间合并的实际决策规则，从而减少给定的起点和目的地之间的总运输成本。XU等[3]通过构建双层规划模型，以减小或者消除供应不确定性在协同物流网络中的不利影响，该模型降低了资源规划变化的规律和成本，从而增加了协同物流网络模型的稳定性。并在此基础上，提出通用两阶段量化框架，使决策者能够在不确定的情况下为协同物流网络模型选择最优的网络设计方案，对协同物流网络模型的稳定性和低成本进行进一步研究[4]。

在集卡研究中集卡路径问题是学者们关注的焦点。Jean-François Cordeau等[5]以集卡运输和等待时间之和最小为目标，构建了集卡路径优化模型，采用局部搜索算法和仿真手段对不同时刻下的集卡运行情况进行了模拟。Kim等[6-7]构建了集卡多目标路径优化模型，以时间和行驶距离最短为目标，并运用整数规划的方法进行求解。Bish等[8]以集卡行驶距离最短为目标，研究了集卡路径问题与进口箱的堆场位置问题。Berghman等[9]将码头集卡作业划分为三个阶段，以时间最短为目标，参考柔性流水车间问题构建了调度模型，并引入枚举搜索树设计了拉格朗日启发式算法来求解。杨静蕾[10]以集卡行驶距离最小为目标提出了集装箱码头物流路径优化模型，获得了集卡最优路径。计明军等[11]以集卡和岸桥作业时间之和最小为优化目标，构建了集卡线路优化模型，并利用改进的进化规划来求解。曾庆成等[12]以总作业时间最小为目标，建立了集卡调度动态模型，并设计了Q学习算法对装卸任务进行分配。曹庆奎等[13]将集卡成本划分为固定成本、可变成本、惩罚成本，分别直接给定单位成本，以最小化作业成本为目标，建立了面向“作业面”的港口集卡路径成本优化模型，并采用遗传蚁群算法求解。

综上，集卡路径相关研究虽然较多，但多以集卡行驶距离或运输时间最小为优化目标。然而，在规定时间内能够完成任务的前提下，码头经营者更为关注运输成本。集卡运输成本由固定成本和可变成本构成，可变成本中很重要一部分就是燃料成本。然而，目前对集卡路径问题的研究中尚未有人从燃料消耗的角度来考虑集卡成本。随着低碳理念和碳税相关制度的逐步确立，减少集卡燃料消耗从而降低碳排放兼具环保和经济意义。

基于上述背景，本文在考虑燃料成本的基础上分两步进行集卡路径优化。基于集卡运输成本对路径进行优化，运输成本中重点分析燃料成本。此部分不考虑集卡数量，主要考虑如何规划路径使集卡运输成本最低。在此基础上，考虑集卡数量的影响，基于集卡作业时间对路径进行优化，主要考虑如何分配任务使所有集卡完成作业的时间最短。对应地分别构建了两个模型，即考虑燃料成本的集卡路径优化模型和考虑集卡作业时间的路径任务分配模型，结合算例分别采用了Lingo和粒子群算法来求解。

由于粒子群算法参数较少，操作较简单；不存在交叉和变异运算，搜索速度快，且具有记忆性，可以保持历史最优解等优点，是解决组合优化问题的一种很好的方法，所以本文中采用粒子群算法对问题进行求解。

1 集装箱码头集卡路径问题描述

假设每辆集卡一次只能运输一个40英尺集装箱(FEU)。集卡作业过程和路径见图1。待卸船舶和待装船舶分别停靠于集装箱码头的泊位1和泊位2，同时进行两船的装卸作业。集卡从泊位1出发，将卸下的进口集装箱运至进口箱区，然后空载到出口箱区提取一个出口集装箱运至泊位2。此作业方式也称为作业面模式。在此过程中集卡主要作业路径为：泊位1→进口箱区→出口箱区→泊位2。由于可能存在装卸不平衡的情况，即待卸集装箱的总量与待装集装箱的总量不相等，除上述路线外，还存在：泊位1→进口箱区，泊位2→出口箱区两种往返路径，分别实现多余进口箱和出口箱的运输任务。三种路径中，集卡的装载情况已在图上标明，其中虚线表示空载。因一次最多只能装载一个集装箱，故集卡只存在满载和空载这两种装载情况。

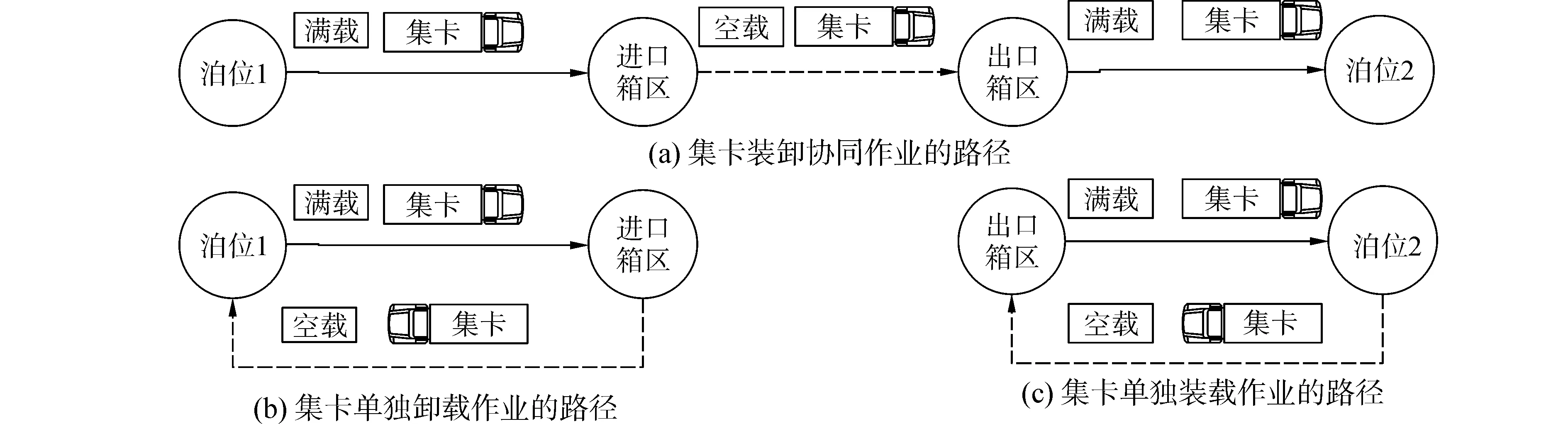
图1 集装箱码头集卡作业的三种路径Fig.1 The three ways of the packing yard trailers

本文中，集卡的路径问题实际上有两层含义，一是在一次作业过程中集卡需要经过哪个进口箱区和哪个出口箱区，二是对于每条相同的路径集卡需要走多少次。把这两个问题归为集卡的初步路径规划问题。在此基础上，对于既定数量的集卡和路径任务，还需在此基础上进一步研究如何给每辆集卡分配任务。本文构建的两个模型分别解决了集卡的初步路径规划问题和进一步的路径任务分配问题。

2 燃料成本计算

燃料成本是车辆运输中可变成本的主要组成部分，研究显示车辆燃料成本受到距离、载重量、速度、路况、燃料消耗率(fuel consumption rate，FCR)等多个因素的影响，Xiao等[14]对车辆燃料消耗研究情况进行了归纳和应用，参考相关文献[14]，本文采用如下燃料成本计算方法：

(1)

本文燃料消耗率是指单位距离的燃料消耗体积。研究表明，燃料消耗率受到车辆载重量和速度的影响，与车辆载重量和速度大致呈正相关关系[14-15]。在集卡作业过程中，假设集卡行驶速度不变。一般来说，运输过程中货物的集散会导致载重量的变化，因此集卡在运输过程中燃料消耗率是变化的。由于集卡运输过程只存在满载和空载两种装载状态，故只对应存在满载燃料消耗率和空载燃料消耗率两种状况。这两项参数参考相关标准和经验值给出。

3 集装箱码头集卡路径优化的两阶段模型

3.1 考虑燃料成本的集卡路径优化模型

3.1.1 参数与变量

决策变量如下：

Xij为集卡沿路径“泊位1→进口箱区i→出口箱区j→泊位2”的运行次数；Yoi为集卡沿路径“泊位1→进口箱区i”之间往返的运行次数；Zrj为集卡沿路径“泊位2→出口箱区j”之间往返的运行次数。

3.1.2 数学模型

假设集卡运输中可变成本仅考虑燃料成本，燃料成本通过式(1)来计算。以包括可变成本和固定成本的集卡运输成本最小为目标函数，构建集装箱码头集卡路径优化模型如下

(2)

s.t.

(3)

(4)

(5)

(6)

Xij≥0,i∈I,j∈E

(7)

Yoi≥0,i∈I

(8)

Zrj≥0,j∈E

(9)

式中：N1为待卸进口集装箱总量；N2为待装出口集装箱总量；I为进口箱区的集合，共有l个箱区；用i表示进口箱区的序号，i=1,2,…,l；E为出口箱区的集合，共有m个箱区；用j表示出口箱区的序号，j=1,2,…,m；doi为泊位1到进口箱区i的距离；用o表示泊位1；drj为泊位2到出口箱区j的距离，用r表示泊位2；dij为进口箱区i到出口箱区j的距离；Qi为第i个进口箱区所能容纳的集装箱数量；Pj为第j个出口箱区已堆存的集装箱数量；c0为单位体积燃料成本；n为集卡数量；ρ0为空载燃料消耗率；ρm为满载燃料消耗率；c′为每辆集卡运输的固定成本。其中，目标函数(2)表示集卡完成所有装卸任务的总成本最小。式(2)：等号右侧前5项反映由集卡燃料成本构成的运输可变成本；第1项表示集卡在泊位1与进口箱区之间满载运输的燃料成本；第2项表示集卡在泊位1与进口箱区之间空载运输的燃料成本；第3项表示当沿路径“泊位1→进口箱区i→出口箱区j→泊位2”运输时，集卡在进口箱区与出口箱区之间空载运输的燃料成本；第4项表示集卡在泊位2与出口箱区之间满载运输的燃料成本；第5项表示集卡在泊位2与出口箱区之间空载运输的燃料成本；第6项为运输固定成本。约束(3)保证所有待卸进口集装箱都能卸载完毕。约束(4)保证所有待装出口集装箱都能装载完毕。约束(5)保证运送到第i个进口箱区的集装箱总数不超过该进口箱区的容量。约束(6)保证第j个出口箱区的已堆存集装箱都能装船。约束(7)～(9)表示决策变量的取值范围。

3.2 考虑集卡作业时间的路径任务分配模型

根据上述模型可以得到集卡的初步路径规划，即需要沿哪些路径来运输集装箱，每条路径需要走多少次。然而实践中通常有多辆集卡共同完成作业，基于初步路径规划的结果，接着需要对每辆集卡进行任务分配。本部分把每条路径的一次运输过程当成一项任务，以所有集卡完成作业的时间最小为目标，建立进一步的优化模型。

已知的相关参数及变量如下：

H为任务集合，任务数量为h；用s表示任务的序号，s=1,2,…,h；N为集装箱卡车的集合，集卡数量为n；用k表示集卡的序号，k=1,2,…,n；Tk为第k辆集卡执行完任务所用的时间；v为集卡行驶速度；Ds为任务s的路程，根据泊位与箱区之间的距离计算得到：

假设所有集卡在作业过程中的行驶速度不变，考虑集卡作业时间构建的路径任务分配模型如下

minT=max{Tk,k∈N}

(10)

s.t.

(11)

(12)

Gks∈{0,1},s∈H,k∈N

(13)

目标函数(10)表示所有集卡完成任务的总时间最短，取完成任务序列中时间最长的集卡作业时间为总时间。约束(11)表示每个任务有且仅有1辆集卡执行，约束(12)给出了每辆集卡作业时间的计算方法，约束(13)表明了决策变量是0～1的变量。

4 模型求解

4.1 考虑燃料成本的集卡路径优化模型求解

待卸船舶停靠于泊位1，有480个进口箱需要卸载。待装船舶停靠于泊位2，有450个出口箱需要装载。码头有5个进口箱区和5个出口箱区，各进口箱区所能容纳的集装箱数量和出口箱区已堆存的集装箱数量见表1及表2。箱区与泊位、箱区与箱区之间的距离见表3。单位体积燃料成本c0=7元/L，集卡的空载燃料消耗率ρ0=0.15 L/km，满载燃料消耗率ρm=0.50 L/km，集卡速度v=10 m/s，每辆集卡固定成本c′=4 000元，集卡数量n=10。

使用Lingo软件对考虑燃料成本的集卡路径优化模型进行求解，得到最优总成本为46 055元，最优路径及沿各路径装卸量见表4。

表1 进口箱区容量

表2 出口箱区堆存量

表3 堆场各点间距离

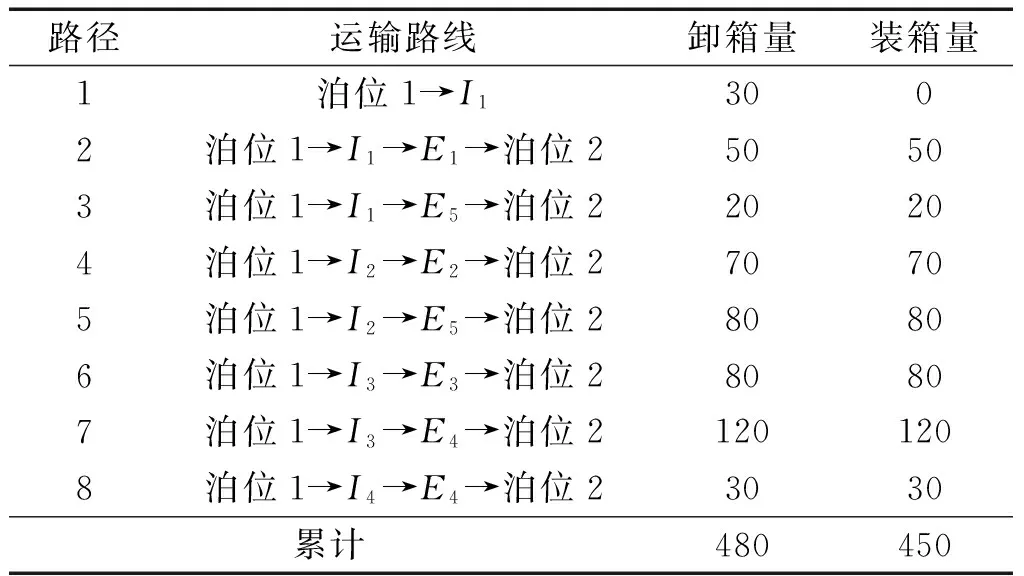
表4 集卡运输路径及装卸箱量Table 4 The route and loading or unloading of the container

在不考虑燃料成本，而以距离最短为目标的传统模型中，根据最优方案计算得到的总成本为46 819元[16]。显然，本文构建的考虑燃料消耗的优化模型得到的结果更优。

4.2 考虑集卡作业时间的路径任务分配模型求解

使用带惯性权重的粒子群算法对集卡路径任务分配模型进行求解，具体步骤如下[17]:

1)初始化粒子群。采用整数编码方式，用长度为h的位置向量Xv来表示各任务的分配情况，Xv中元素的取值代表集卡序号，Xv取值范围为1～n(集卡数量)。在该算例中，n=10。编码过程见表5，Xv表示执行各任务的集卡序号。随机生成位置向量Xv和速度向量Vv，保证Xv每一维取1～n之间的整数，Vv每一维取-(n-1)～(n-1)之间的整数。

表5 编码示意

2)计算适应值函数。利用式(10)、(12)计算适应值函数，以此作为粒子评价标准。

3)重复以下步骤，直到满足迭代终止条件。

①对每一个粒子，按位置和速度公式进行更新，超过边界范围时按边界取值。速度及位置更新公式如下：

(14)

(15)

式中:c1和c2是学习因子，r1和r2是随机数，pbest是当前粒子的历史最优位置，gbest是所有粒子的历史最优位置。ω是线性递减的惯性权重，采用如下公式计算：

(16)

式中：ωmax是初始权重，ωmin是最终权重，itermax是最

大迭代次数，iter是当前迭代次数。

②用适应值函数评价所有粒子。

③若某个粒子的当前适应值优于历史最优适应值，则记当前适应值为历史最优适应值。同时记下此时的粒子位置为该粒子历史最优位置。

④寻找当前各粒子群内的最优解和总群体最优解，若优于历史最优解则更新pbest和gbest。对于子群内有多个最优值，则随机取其中一个为子群内当前最优解。

4)设置迭代终止条件。以最大迭代次数为算法停止条件。

基于粒子群算法使用Matlab对考虑集卡作业时间的路径任务分配模型进行求解，得到各集卡任务分配及作业时间情况见表6。表中列出了各集卡沿各路径的运输次数，即相应任务数量。取集卡中完成任务时间最长者为总作业时间，为5.27h。

表6 集卡任务分配及作业时间

5 结论

对于集装箱码头的集卡路径问题，本文综合考虑了燃料消耗情况和作业时间两个因素，构建两阶段模型对集卡路径优化进行研究。综合两个模型，既考虑了燃料成本又考虑了作业时间，与实际码头经营者的关注点相一致。通过本文中的研究，主要得出如下结论：

1)通过构建的考虑燃料消耗的优化模型得到的总成本小于传统模型中以距离最短为目标的根据最优方案计算得到的总成本。

2)通过构建的两阶段集卡路径优化模型，可以在降低总成本的基础上，降低集卡的作业时间，对集卡路径进行进一步优化。

在考虑燃料成本的情况下，从成本和时间两个角度对集卡路径进行优化。研究还不够深入，应在本文研究的基础上，从等待时间、固定成本、可变成本等多维角度，对集卡路径优化问题进行进一步研究。

[1] 周林，王旭，林云，景熠. 面向空间分布式小批量物流供需的多任务集成调度[J]. 计算机集成制造系统， 2016， 22(3)： 822-832.

ZHOU Lin, WANG Xu, LIN Yun, et al. Integrated multi-task scheduling for spatially distributed small-batch logistics[J]. Computer integrated manufacturing systems, 2016， 22(3)： 822-832.

[2] BOOKBINDER J H，HIGGINSON J K. Probabilistic modeling of freight consolidation by private carriage [J]. Transportation research part E: logistics and transportation review, 2002, 38(5): 305-318.

[3] XU X F，ZHANG W，LI N，et al. A bi-level programming model of resource matching for collaborative logistics network in supply uncertainty environment [J]. Journal of the Franklin institute, 2015, 352(9): 3873-3884.

[4] XU Xiaofeng, HAO Jun, DENG Yirui, et al. Design optimization of resource combination for collaborative logistics network under uncertainty[J]. Applied soft computing, 2017, 560(7): 684-691.

[5] CORDEAU J F, LEGATO P, MAZZA R M, et al. Simulation-based optimization for housekeeping in a container transshipment terminal[J]. Computers & operations research, 2015, 53: 81-95.

[6] KIM K H, BAE J W. A look-ahead dispatching method for automated guided vehicles in automated port container terminals[J]. Transportation science, 2004, 38(2): 224-234.

[7] KIM K H. A pooled dispatching strategy for automated guided vehicles in port container terminals [J]. International journal of management science, 2000, 6(2): 47-67.

[8] BISH E K, LEONG T Y, Li C L, et al. Analysis of a new vehicle scheduling and location problem[J]. Naval research logistics (NRL), 2001, 48(5): 363-385.

[9] BERGHMAN L, LEUS R. A Lagrangian heuristic for a dock assignment problem with trailer transportation[C]// 2010 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM). [S.l.], 2010: 1376-1380.

[10] 杨静蕾. 集装箱码头物流路径优化研究[J]. 水运工程, 2006(1): 32-35.

YANG Jinglei. Logistics routing optimization of constainer[J]. Port & waterway engineering, 2006(1): 32-35.

[11] 计明军, 靳志宏. 集装箱码头集卡与岸桥协调调度优化[J]. 复旦学报: 自然科学版, 2007, 46(4): 459-464.

JI Mingjun, JIN Zhihong. A united optimization of crane scheduling and yard trailer routing in a container terminal[J]. Journal of Fudan University: Natural Science, 2007, 46(4): 459-464.

[12] 曾庆成, 杨忠振. 集装箱码头集卡调度模型与Q学习算法[J]. 哈尔滨工程大学学报, 2008, 29(1): 1-4.

ZENG Qingcheng, YANG Zhongzhen. A scheduling model and Q-learning algorithm for yard trailers at container terminals[J]. Journal of Harbin Engineering University, 2008, 29(1):1-4.

[13] 曹庆奎, 赵斐. 基于遗传蚁群算法的港口集卡路径优化[J]. 系统工程理论与实践, 2013, 33(7): 1820-1828.

CAO Qingkui, ZHAO Fei. Port trucks route optimization based on GA-ACO[J]. Systems engineering-theory & practice, 2013, 33(7): 1820-1828.

[14] XIAO Y, ZHAO Q, KAKU I, et al. Development of a fuel consumption optimization model for the capacitated vehicle routing problem[J]. Computers & operations research, 2012, 39(7): 1419-1431.

[15] 吴丽荣,胡祥培,饶卫振. 考虑燃料消耗率的车辆路径问题模型与求解[J]. 系统工程学报, 2013, 28(6): 804-811.

WU Lirong, HU Xiangpei, RAO Weizhen. New capacity-vehicle-routing-problem model and algorithm for reducing fuel consumption[J]. Journal of systems engineering, 2013, 28(6): 804-811.

[16] 赵金楼, 黄金虎, 刘馨. 集装箱码头的集卡两阶段路径优化研究[J]. 中国管理科学, 2017(4): 152-157.

ZHAO Jinlou, HUANG Jinhu, LIU Xin. Two-stage optimization for yard trailers routing in container terminals [J]. Chinese jurnal of management dcience, 2017(4): 152-157.

[17] 纪震, 廖惠连, 吴青华. 粒子群算法及其应用[M]. 北京：科学出版社, 2009.

JI Zhen, LIAO Huilian, WU Qinghua. Particle swarm optimization and application [M]. Beijing：Science Press, 2009.

本文引用格式：

赵金楼， 黄金虎， 刘馨， 等. 考虑燃料成本的集装箱码头集卡路径优化[J]. 哈尔滨工程大学学报， 2017， 38(12): 1985-1990.

ZHAO Jinlou, HUANG Jinhu, LIU Xin, et al. Optimization for routing yard trailers in container terminals by considering fuel cost[J]. Journal of Harbin Engineering University， 2017， 38(12): 1985-1990.