气泡高速艇波浪中阻力及运动性能数值研究
欧勇鹏, 周广礼, 吴浩
(海军工程大学 舰船工程系,湖北 武汉 430033)
目前,船舶气层减阻技术已在俄罗斯、乌克兰、日本、荷兰等国家获得了广泛应用,取得了显著的军事经济效益[1]。我国自20世纪80年代开始,在该领域开展了相关理论及试验研究,取得了静水中模型绝对减阻率达20%~25%的效果[2-4],但至今尚未实现实艇应用,主要原因即是在考虑风浪作用下气泡高速艇的减阻效果及运动性能尚未明确。气泡高速艇在波浪中是否仍然具备良好的减阻效果?波浪中的艇底气层是否能保持稳定状态?气层作用下高速艇在波浪中的运动性能如何?气层与摇荡运动艇体之间的相互作用力学规律如何?这一系列问题尚需深入研究和解答。
针对以上问题,国内外公开发表的相关理论及试验研究不多。在试验研究方面,董文才等[5-6]通过拖曳水池试验探索了波浪中的气层减阻效果以及气层对艇体运动的影响规律,但鉴于试验条件限制,未能给出艇体运动、气层形态、阻力的同步变化过程。在理论研究方面,美国的Jin-Keun Choi等[7]联合采用面元法与求解URANS的方法研究了喷气下瘦长型船的船体兴波、气层形态及船体运动对气层分布的影响,但该方法在计算船体兴波时采用线性势流理论,不适用于计算高速艇的喷溅等非线性流动问题。
为此,本文考虑了高速艇流场的强非线性及气-液两相流的复杂性,采用粘性CFD的方法,从波浪中阻力、纵向运动及气层形态等角度进行研究,试图通过理论计算揭示波浪中气层-艇体的相互作用过程,掌握气泡高速艇在波浪中的航行性能。
1 数值波浪水池
1.1 研究对象
计算对象为一条底部设置凹槽的B.H.型气泡高速艇模型,主尺度参数如表1所示,图1给出了艇体及底部凹槽的三维效果图。其中,Δ为排水量,L为艇体总长,LP为折角线长,BPX为折角线最大宽度,βM为中部艇底斜升角,βT为尾部艇底斜升角;LP/BPX表示折角线长与折角线最大宽度之比,HB/BPX表示艇体凹槽深度与折角线最大宽度之比,SBH/SP表示水平面上的艇底凹槽投影面积与折角线投影面积之比,Ryy/L表示纵向惯性半径与艇长之比。

表1 计算模型的主尺度参数

图1 计算对象三维视图Fig.1 3-D geometry model of hull
1.2 两相流模型
气-液两相流采用VOF模型(volume of fluid model),界面追踪采用高分辨率HRIC方法(high-resolution interface capturing scheme)。考虑界面压缩修正的VOF方法的控制方程如式(1)~(5)所示,详细可参见文献[8]。
质量守恒方程:
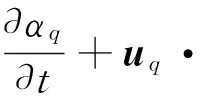
(1)
动量方程:
-αqp+·(μqαquq)+
ρqαqg+FD,q+Fs,q
(2)
式中:ρq、αq和uq分别表示第q相的密度、体积分数和流动速度;FD,q和Fs,q分别为相间曳力与表面张力,本文计算过程中忽略了这两项的影响;uc为界面压缩速度,其表达式为uc=Cα|u|(α/|α|),式中|u|为流动速度,Cα为锐化因子,取值范围为0~1。
界面追踪采用高分辨率HRIC格式,其基础是NVD方法(normalized variable diagram),原理示意图如图2所示。图中,αD、αA、αU分别表示施主单元、受主单元及迎风单元的体积分数,αf表示控制体边界的体积分数,其计算表达式为:

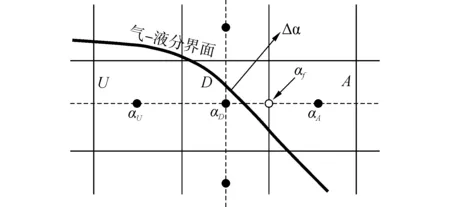
图2 NVD方法原理示意图Fig.2 The schematic diagram of NVD method

图3 角度θf的定义Fig.3 Definition of angle θf
HRIC方法在求解过程中考虑了界面与网格夹角、当地库朗数等因素的影响,其求解的主要方程和步骤如下[9-10]:
1)采用NVD方法计算归一化体积分数
(3)
2)考虑角度θf的影响,通过权重因子γf对界面伪变形进行修正。
(4)
式中:θf定义为施主单元D指向受主单元A的单元向量d与界面法向n之间的夹角(如图3所示),γf=(cosθ)Cθ,C0称为角度因子。
3)考虑当地库朗数的影响,对计算的不稳定性进行修正。
(5)
式中:CUL为库朗数下界值,CUU为库朗数上界值,Cf为当地库朗数。
1.3 湍流模型
湍流模型采用在船舶流体性能计算中被广泛应用和验证的Realizablek-ε模型[11-12],其基本数学表达形式如下。
湍动能方程(k方程):
(6)
耗散率方程(ε方程):
(7)

(8)
(9)

1.4 数值造波
数值波浪采用线性波,无限水深下的波浪参数满足:
(10)
式中:ω为圆频率,k为波数,a为波幅,U为边界入口处的流体速度,x和z分别为流体的纵向和垂向坐标位置。此外,为保持压力出口边界条件的稳定性,在距离压力出口1倍艇长区域内添加阻尼项,动量源的函数表达形式为
(11)

1.5 计算域及网格
考虑到流动关于艇体中纵剖面对称,仅对流场的一半进行网格离散。计算流域分成随艇体一起运动的重叠网格区域和固定不动的背景区域,如图4所示。这两个区域均采用剪切型网格进行离散,区域之间的数据传递采用重叠网格技术。
重叠网格区域前方距艇艏0.25L,后方距艇艉0.3L,上表面距甲板为0.3L,下表面距艇底0.25L,侧面距舷侧为0.3L,均设置为重叠网格边界。中纵剖面设置为对称面,艇体表面设置为无滑移物面,喷气口位于艇底凹槽的艏部,设置为速度入口。
背景区域在计算过程中保持静止,该区域总长5.5L、总宽2L、总高3.1L,上表面距离艇体甲板为1.3L,下表面距离艇底部为1.7L,侧面距离艇体舷侧为1.8L,均设置为对称面;入口距离艇艏为1.5L,设置为速度入口;出口距离艇艉为3.0L,设置为压力出口;中纵剖面设置为对称面。
图5给出了重叠网格区域及背景区域的网格划分情况。对艇底凹槽、艏部喷溅及艉部兴波等区域进行了网格加密,艇体附近的网格尺度为5 mm,喷溅处的网格尺度为3 mm,边界层网格厚度为3 mm,设置4层网格,沿法向的增长率为1.25。对自由液面附近的网格进行了加密,垂直自由液面方向的网格尺度为4 mm,同时为保证艇体姿态变化过程中重叠区的网格尺度基本相同,自由液面加密区的高度在重叠网格区域中为0.06 m,在背景区域中为0.1 m,且在两者相互重叠的位置处进行适当增加(如图5(b)所示)。网格总数为120万,其中重叠网格区域的网格数为90万,背景区域的网格数为30万。
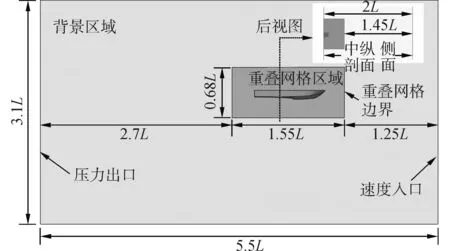
图4 区域划分与边界条件Fig.4 Calculation region and boundary condition

图5 计算区域的网格划分Fig.5 The meshes of calculation region
2 数值方法验证
艇体纵摇和垂荡的计算采用6-DOF刚体运动模型,仅计及沿垂直方向的平动及绕横轴方向的转动,限制了其余自由度的运动。非稳态时间离散采用二阶格式,时间步长Δt=5.0×10-4s。空气的密度为1.184 kg/m3,动力粘性系数为1.855×10-5Pa·s;水的密度为997.561 kg/m3,动力粘性系数为8.887×10-4Pa·s。
在计算过程中为避免气-液相在艇体表面发生伪扩散现象,考虑模型尺度、航速、时间步长等因素的影响,HRIC-VOF方法的主要参数取值为Cа=0.7、Cθ=0.5、CUL=0.5、CUU=6.0,其中模型试验在中国特种飞行器的高速拖曳水池中进行,试验结果可参见文献[14]。
2.1 数值波浪
图6给出了波长λ=4.0 m、波高hw=0.06 m时充分发展后的波形图像以及距离区域入口1.5L处(艇艏所在位置)数值计算波升与理论结果的对比。从图6可以看出:采用本文的数值造波方法可以清晰表达所需的数值波浪,计算所得波形与理论值吻合较好,验证了本文数值造波方法的有效性。
2.2 静水阻力
图7给出了饱和喷气下的阻力、纵倾计算值与试验值的对比,图中Rt/Δ为单位排水量阻力。从图7可以看出:采用该数值方法计算所得阻力、纵倾值与试验结果吻合较好,阻力最小相对偏差可达1.48%,最大相对偏差为4.59%;纵倾值的最小相对偏差可达3.10%,绝对偏差值为0.14°。可见,该数值计算方法计算艇体阻力及航行姿态且具备较好的精度。图8给出了FV=2.80时,艇体兴波及气层形态图像的计算结果。通过试验过程中的观察发现,计算所得兴波及艇底气层在形态上与试验结果基本一致。
2.3 顶浪中的纵向运动
图9给出了喷气流量Q=12 m3/h、容积傅汝德数FV=2.24、波长船长比λ/Lp=2.171、波高船长比hw/Lp=0.021 7时艇体垂荡与纵摇的时历过程。图中k为入射波的波数,ζa为波幅,ZG为垂荡值,θ为纵摇角。从图中可以看出,当时间t>15 s后,艇体运动处于稳定波动状态。
图10为艇体运动稳定状态下无因次垂荡、纵摇与试验结果的对比。从图中可以看出,垂荡与纵摇的计算结果与试验结果吻合较好,垂荡幅值与试验结果的偏差为6.4%,纵摇幅值与试验结果的偏差为2.8%。说明该数值计算方法求解艇体在波浪中的摇荡运动具备较好的可靠性。

图6 数值造波及结果分析Fig.6 Numerical wave patterns and its Comparison with theoretical value

图7 数值计算结果与试验值的对比Fig.7 Comparison of numerical results with experimental results

图8 艇体兴波及艇底气层数值计算与试验观测的对比Fig.8 Comparison of spray and air cavity pattern of numerical results with experimental results

图9 垂荡与纵摇的时历计算过程Fig.9 the time history of heave and pitch
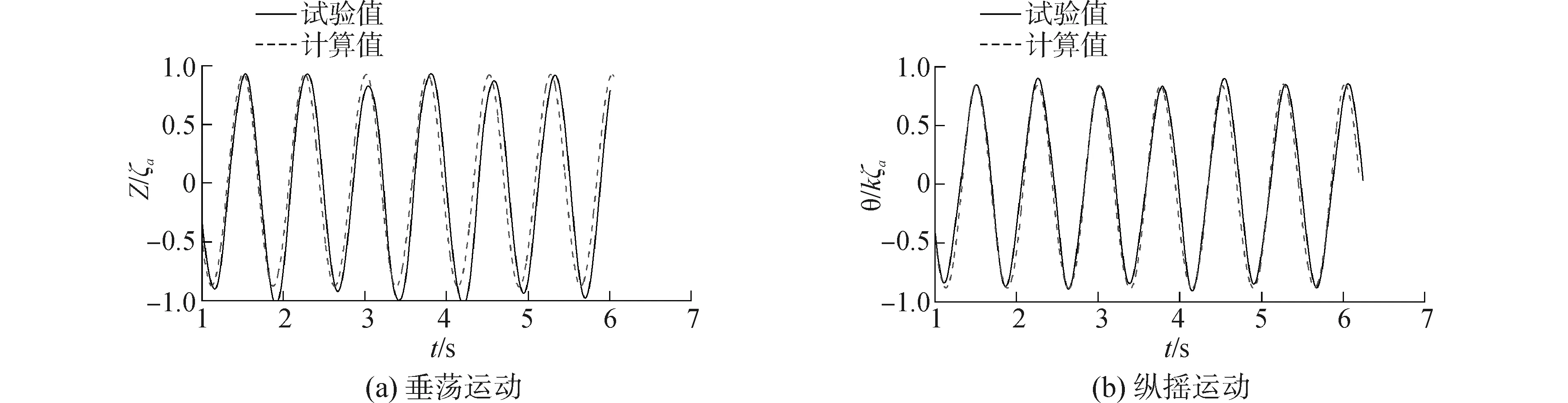
图10 垂荡与纵摇曲线与试验结果的对比Fig.10 Comparison of heave and pitch numerical results with experimental results
3 气层对波浪中阻力及纵向运动性能的影响
3.1 气层对波浪中阻力的影响
图11给出了FV=2.24时波浪中喷气前后的总阻力变化,此时波长λ/LP=2.171、波高hw/LP=0.021 7、气流量Q=12 m3/h。从图中可以看出:在波浪作用下,艇体阻力随时间呈周期性波动,气层可使波浪中的阻力大幅度降低。

图11 喷气对波浪中阻力的影响Fig.11 The effect of air cavity on hull resistance in wave
表2给出了不同波长下喷气前后艇体平均阻力及减阻率的变化,从表中可以看出:在不同波长下,气层均可使阻力大幅度降低,减阻率可达27.53%~30.41%;从表2中还可以看出,随着波长增长,减阻率呈增大趋势。
表2不同波长下喷气对阻力及减阻率的影响
Table2Theeffectofairinjectiononhullresistanceatdifferentwavelength
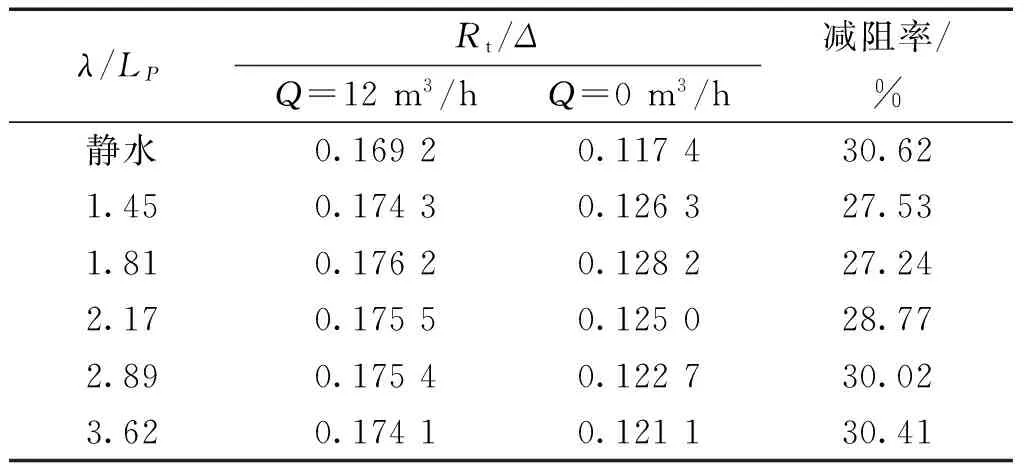
λ/LPRt/ΔQ=12m3/hQ=0m3/h减阻率/%静水0.16920.117430.621.450.17430.126327.531.810.17620.128227.242.170.17550.125028.772.890.17540.122730.023.620.17410.121130.41
图12给出了不喷气及喷气下波浪中阻力相对静水阻力的增加量随波长的变化,图中ΔR/R表示波浪中的阻力增加与静水阻力之比。从图中可以看出:喷气及不喷气条件下艇体阻力增值随波长的变化规律相类似;但气层作用下艇体在波浪中的阻力增值有所增大;随着波长增加,两者阻力增值的百分比趋于相同。
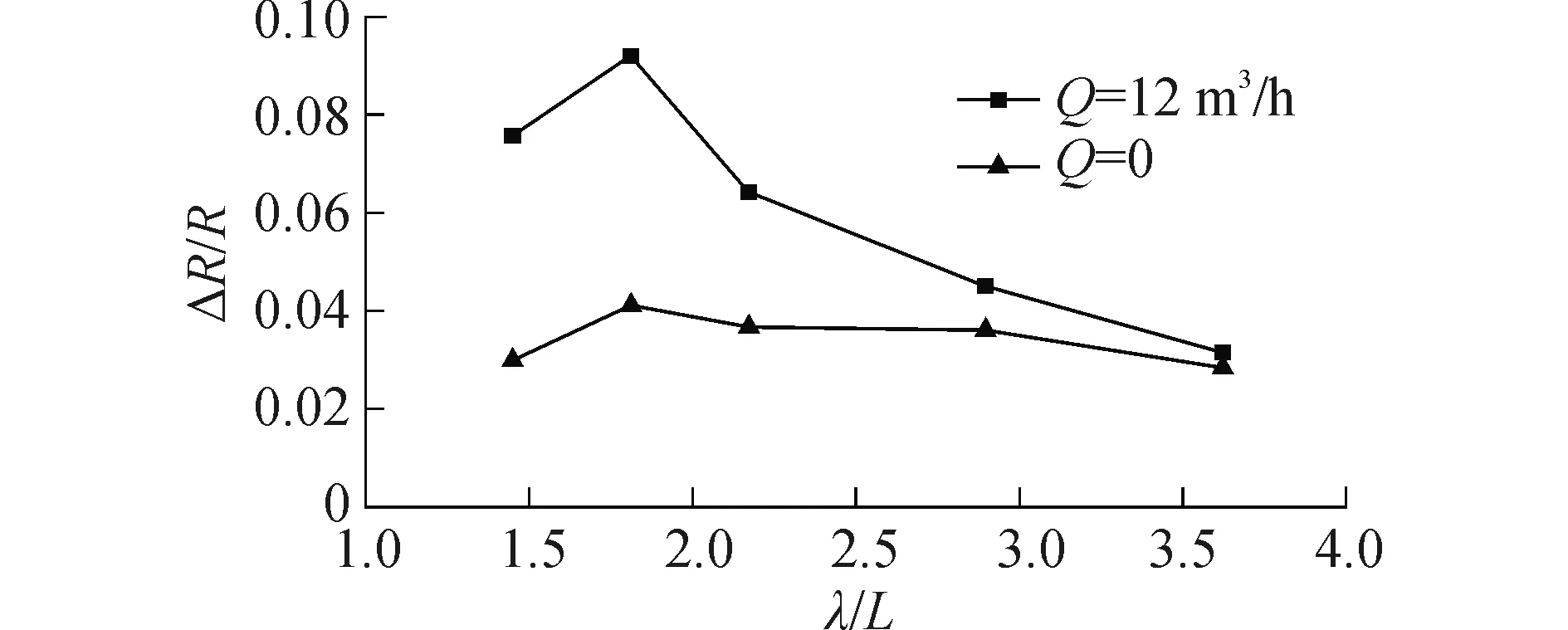
图12 相对静水的阻力增加随波长的变化Fig.12 The add resistance in different wave length
3.2 气层对纵向运动的影响
图13给出了喷气前后艇体垂荡、纵摇时历曲线的对比,此时航速FV=2.237,波长λ/LP=2.17,波高hw/LP=0.021 7,喷气时的气流量Q=12 m3/h。图14给出的是艇体运动处于稳定波动状态下时中心化时历曲线(去均值)的对比情况。
从图13看出:喷气使得垂荡和纵摇运动的波动中心发生变化,气层使得垂荡运动的平均值增大,而纵摇运动的平均值略有降低。去除波动运动的中心值后发现:气层对垂荡运动幅值的影响不大,使纵摇运动幅值略有降低(如图14所示)。
图15给出了不同波长下,喷气前后艇体垂荡与纵摇响应的变化。从图15中可以看出:顶浪规则波中,艇体气层对垂荡运动响应的影响不大,对纵摇运动响应有所影响;喷气使得纵摇运动响应有所减小,且随着波长增长,气层导致的纵摇响应减小量呈增大趋势。
4 艇体运动对气层形态及其稳定性的影响
4.1 气层面积
图16给出了稳定运动状态下,艇底气层面积覆盖率随时间的变化,此时的波高、喷气量、波浪等参数与上一节计算工况完全相同。其中,气层面积覆盖率是指气层面积SA与艇底凹槽面积SBH之比,表征了气层在凹槽中所占有的面积比率。
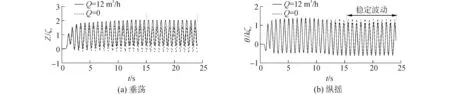
图13 喷气及不喷气下艇体纵向运动时历曲线对比Fig.13 The comparison of longitudinal motions between with and without air cavity

图14 中心化后的纵向运动波动曲线对比Fig.14 The comparison of longitudinal motions after subtraction of mean value

图15 不同波长下气层对垂荡与纵摇响应的影响Fig.15 The effect of air cavity on heave and pitch at different wave length
从图16可以看出:在波浪作用下,气层面积覆盖率呈周期性波动,这表征了艇体运动对气层形态的干扰作用;波长不同,气层面积覆盖率的波动情况略有不同,但差别不大。
表3给出了不同波长下,气层平均覆盖率、波动幅值的统计结果,从表中可以看出:在不同波长下,气层在凹槽中的平均覆盖率可达78.67%~83.76%,且波动幅值仅为6.92%~9.54%,说明气层在纵向规则波中未发生严重破碎现象,具备良好的稳定性,这正是B.H.型气泡高速艇在顶浪中仍然具备良好减阻效果的主要原因。
4.2 气层形态
图17给出了波长λ/LP=2.171下艇底气层在一个运动周期中的变化过程,航速、波长、波高、喷气量等参数与上一节的计算相一致。图中,t1时刻表示纵摇角位于波谷位置,t2时刻表示纵摇角位于从下往上穿过平衡位置,t3表示纵摇位于波峰位置,t4表示纵摇位于从上往下穿过平衡位置。从图中可以看出:在一个纵摇运动周期过程中,气层基本上均能填满整个底部凹槽,其形态与艇底凹槽形状接近;除了气层尾部发生小量变化外,其余变化不大。这说明采用设置凹槽的艇底构型,可较好地保持气层在顶浪航行状态下的稳定性。
表3波浪中气层覆盖率的平均值及波动情况
Table3Theaveragevalueofaircavitycoverratioonbottomhollow
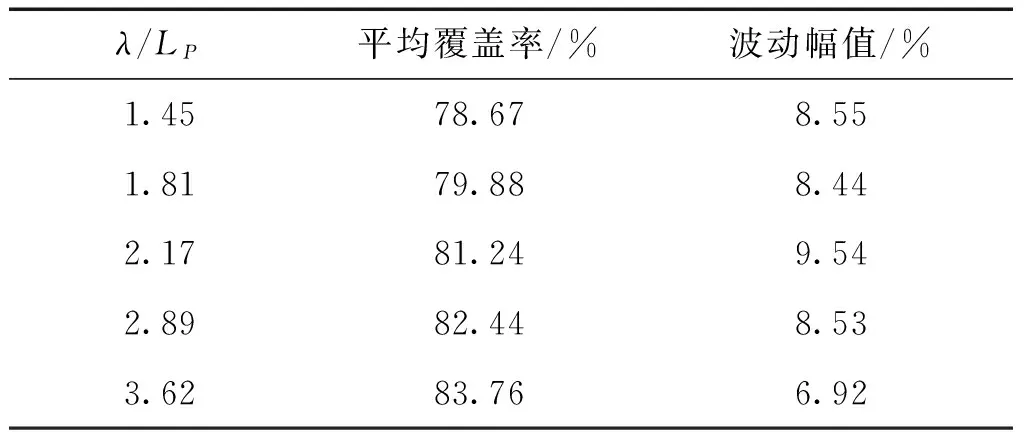
λ/LP平均覆盖率/%波动幅值/%1.4578.678.551.8179.888.442.1781.249.542.8982.448.533.6283.766.92

图16 气层面积覆盖率随时间的变化曲线Fig.16 Time history of air cavity cover ratio on bottom hollow
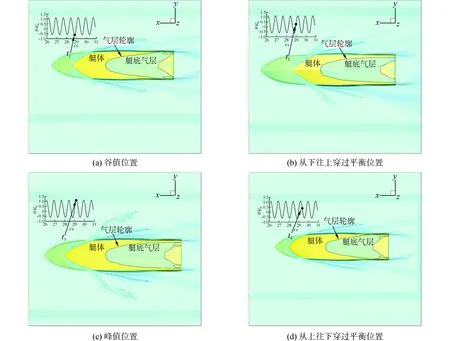
图17 艇底气层的形态变化Fig.17 The change history of air cavity pattern within a period of wave
5 结论
1)采用HRIC-VOF方法、Overset网格技术及刚体6-DOF模型相结合,可有效计算气层作用下高速艇波浪中的阻力、垂荡、纵摇及气层形态。
2)B.H.型气泡高速艇在顶浪中仍可取得良好的气层减阻效果,波长对减阻率有所影响,但影响不大。
3)气层对顶浪条件下B.H.型气泡高速艇垂荡的影响甚微;气层对纵摇有所影响,喷气可使纵摇响应减小。
4)顶浪条件下,气层在凹槽中的覆盖率可达78.67%~83.76%,气层面积变化不大,这是该型艇在波浪中仍具备良好喷气减阻效果的主要原因。
[1] SVERCHKOV A V.Application of air cavities on high-speed ships in Russia[C]// Proceeding of the International Conference on Ship Drag Reduction SMOOTH-SHIPS. Istanbul, Turkey, 2010: 20-24.
[2] 董文才.滑行艇及平板气层减阻的研究[D].武汉:海军工程大学,2003.
DONG Wencai. Study on the effect of air layer on planning craft and flat plate[D]. Wuhan: Naval University of Engineering, 2003.
[3] 董文才,郭日修,陈小玲,等.滑行艇气层减阻试验[J].中国造船, 2002, 43(4): 13-18.
DONG Wencai,GUO Rixiu,CHEN Xiaoling,et al.Experimental study on resistance reduction of planning craft by air[J].Shipbuilding of China, 2002, 43(4): 13-18.
[4] 唐桂林,倪其军,王丽艳,等.高速气泡艇阻力数值模拟及气泡减阻效果分析[J].船舶力学, 2014, 8(18): 882-888.
TANG Guilin, NI Qijung, WANG Liyan, et al. Numerical evaluation of the resistance reduction effect for three-dimensional high-speed air cavity craft[J]. Journal of ship mechanics, 2014, 8(18): 882-888.
[5] DONG Wencai,OU Yongpeng.Experimental study on resistance and longitudinal motion of high-speed air cavity craft[J].Journal of ship mechanics, 2011, 9(15): 950-959.
[6] 欧勇鹏,董文才,许勇.B.H型气泡高速艇规则波中纵向运动试验研究[J]. 中国造船, 2010, 51(3): 1-10.
OU Yongpeng, DONG Wencai, XU Yong. Experimental study on the longitudinal motion performances of bottom hollowed high speed air craft in regular wave[J].Shipbuilding of China, 2010, 51(3): 1-10.
[7] JIN-KEUN C,CHAO-TSUNG H,GEORGES L.Numerical studies on the hydrodynamic performance and the startup stability of high speed ship hulls with air plenums and air tunnels[C]//Ninth International Conference on Fast Sea Transportation FAST2007.Shanghai,China, 2007: 476-484.
[8] MUZAFERIJA S, PERIC M, SAMES P, et al. A two-fluid Navier-Stokes solver to simulate water entry[C]//Proc Twenty-Second Symposium on Naval Hydrodynamics. 1998.
[9] SHONIBARE O Y,WARDLE K E.Numerical investigation of vertical plunging jet using a hybrid multifluid-VOF multiphase CFD solver[C]//International Journal of Chemical Engineering.[S.l.], 2015, 925639.
[10] WACLAWCZYK T, KORONOWICZ T. Comparison of CICSAM and HRIC high-resolution schemes for interface capturing[J]. Journal of theoretical and applied mechanics, 2008, 46(2): 325-345.
[11] SHIH T H, LIOU W W, SHABBIR A, et al. A new k-ε eddy-viscosity model for high Reynolds number turbulent flows-model development and validation[J]. Computers & fluids, 1995, 24(3): 227-238.
[12] YONG Xua, ZHANG Guoqing. Numerical calculation for the flow in the air-thrust bearings[C]//Procedia Engineering. [S.l.], 2011: 922-927.
[13] FENTON J D. A fifth-order stokes theory for steady waves[J]. J waterway, port, coastal and ocean engineering, 1985,111(2): 216-234.
[14] 欧勇鹏.气泡高速艇水动力性能研究[D].武汉:海军工程大学, 2009.
OU Yongpeng. Study on hydrodynamic performance of high speed air cavity craft[D]. Wuhan: Naval University of Engineering, 2009.
本文引用格式:
欧勇鹏, 周广礼, 吴浩. 气泡高速艇波浪中阻力及运动性能数值研究[J]. 哈尔滨工程大学学报, 2017, 38(12): 1849-1857.
OU Yongpeng, ZHOU Guangli, WU Hao. Numerical investigation of the effects of air cavity on the resistance and longitudinal motion of a high-speed air cavity craft in regular waves[J]. Journal of Harbin Engineering University, 2017, 38(12): 1849-1857.

