多元时间序列缺失数据填补方法

李正欣, 张凤鸣, 王 瑛, 陶 茜, 李 超

(空军工程大学装备管理与无人机工程学院, 陕西 西安 710051)

0 引 言

按时间顺序获取的一系列观测值xt(j)称为时间序列,其中,t(t=1,2,…,n)表示第t个时刻,j(j=1,2,…,m)表示第j个变量,xt(j)表示第j个变量在第t个时刻上的记录值[1]。当m=1时,xt(j)为一元时间序列;当m>1时,xt(j)为多元时间序列。

时间序列广泛存在于气象、水文、医学和经济等众多领域[2]。与一元时间序列相比,多元时间序列更具一般性,例如,股票交易记录包含交易量、开盘价、收盘价、最高价和最低价[3];“黑匣子”记录的飞行数据包含速度、高度、俯仰角、倾斜角和航向角等。广义上,任何包含多变量的数据存储都可以视为多元时间序列[4]。

时间序列中隐含着深层知识,针对时间序列的数据挖掘已成为目前数据挖掘领域中的研究热点[5]。然而,在实际应用中,数据采集受多种因素的干扰,难免存在缺失数据,造成序列不连续,从而影响后续的分析处理。在数据挖掘领域UCI公开数据集中,超过40%的数据库都含有缺失数据[6]。因此,研究多元时间序列的缺失数据填补方法是分析处理时间序列的前提、具有重要的应用价值。

1 相关研究

传统的数据填补方法有均值填补、回归填补、期望值最大化方法等[7],这些方法计算简单,但当缺失数据量较多、波动较大时,填补精度大幅度下降。

随后在传统方法基础上,又融入了统计分析、机器学习等方法,在一定程度上提高了填补精度。然而,这些成果主要针对传统数据类型,多元时间序列在时间维和变量维上,都具有较强的相关性,与传统数据具有较大的差异,因此,这些方法并不完全适用于多元时间序列。

目前,针对多元时间序列填补方法的研究成果相对较少[7],主要有多元回归、神经网络、支持向量机(support vector machine,SVM)和组合填补方法等。

多元自回归模型[8]是一种经典的时间序列分析方法,它适用于线性模型,但对非线性的时间序列效果不佳。

神经网络[9]可以对任意非线性函数进行逼近,具有非线性、自学习的特点,可用于时间序列缺失数据填补。但基于经验风险最小化原则,要求较大的样本规模,对于小样本情况,容易出现过拟合、泛化能力不足等问题。

SVM[10]追求结构风险最小化,专门针对有限样本,得到现有信息下的全局最优解,且计算复杂度与维度无关。然而,大多数基于SVM的填补方法[11-12],仅关注缺失数据所属的单变量信息,没有针对多元时间序列的特点、有效利用其他相关的多变量信息。文献[13]提出了一种基于状态匹配与SVM的多变量填补方法。首先,判断存在缺失数据的序列所属的类;然后,分析该类序列中,同缺失数据所属变量相关的其他变量;最后,在相关变量中选择样本点,使用SVM填补缺失数据。然而,该方法在判断序列所属类别及分析相关变量时,使用人工判读,对经验依赖性较强。

文献[14]提出基于最小二乘支持向量机(least squares support vector machine,LSSVM)的组合权重填补方法,同时利用缺失数据所属的单变量以及与其相关的多变量信息,对单变量填补值与多变量填补值加权求和,作为最终填补结果。然而,该方法用一个权重值处理所有的缺失数据,难以体现各个缺失数据的差异性;此外,权重值在真实数据已知的情况下才能得到最优结果,限制了该方法的使用。

时间序列通常具有非平稳、非线性、非结构化等特征,此外,具有典型模式的序列通常样本规模较小。针对以上特征,提出一种基于LSSVM的组合阈值填补方法。首先,以存在缺失数据的多元时间序列为对象,搜索与其同类的相似序列;然后,利用LSSVM分别进行多变量填补和单变量填补;最后,根据多变量和单变量填补结果的差异度,进行组合阈值填补。

2 基于LSSVM的组合阈值填补

LSSVM把最小二乘线性系统引入到SVM中,将解二次规划问题转化为求解线性方程组,能有效提高求解速度与泛化能力[15]。

2.1 LSSVM

训练样本集D={(xk,yk)}中:xk∈Rn表示输入、yk∈R表示输出,原始空间中的函数估计转化为求解[14]

s.t.yk=ωTφ(xk)+b+ek,k=1,2,…,N

(1)

式中,γ为正则化参数；φ(·):Rn→Rnb是核空间映射函数；权矢量ω∈Rnb；误差变量ek∈R；b是偏差量。

可以构造拉格朗日方程求解最优化问题为

L(ω,b,e,α)=J(ω,e)-

(2)

拉格朗日乘子αk∈R。令L对ω,b,ek,αk的偏导数分别等于0,消去ek和ω可得

(3)

式中,Ω=K(xk,xl)=φ(xk)Tφ(xl)；y=[y1,y2,…,yN]T;α=[α1,α2,…,αN]T;1v=[1,1,…,1]T。

根据Mercer条件,存在映射函数φ和核函数K(·,·)使得

K(xk,xl)=φ(xk)Tφ(xl)

(4)

则LSSVM的函数估计为

(5)

α、b由式(3)求解得到。

2.2 组合阈值填补方法

利用LSSVM填补缺失数据有两种基本思路:单变量填补和多变量填补。单变量填补只利用缺失数据所属的单变量信息,进行支持向量回归,填补缺失数据。多变量填补利用与缺失数据所属变量相关的其他多个变量信息,对缺失数据进行填补。

单变量填补依据变量自身的内在规律,多变量填补利用变量间的相互关系。组合阈值填补方法同时利用单变量和其他多个相关变量信息。

不失一般性,设数据集中,序列X1的第i个变量维度上存在缺失数据。组合阈值填补方法的基本流程如图1所示。

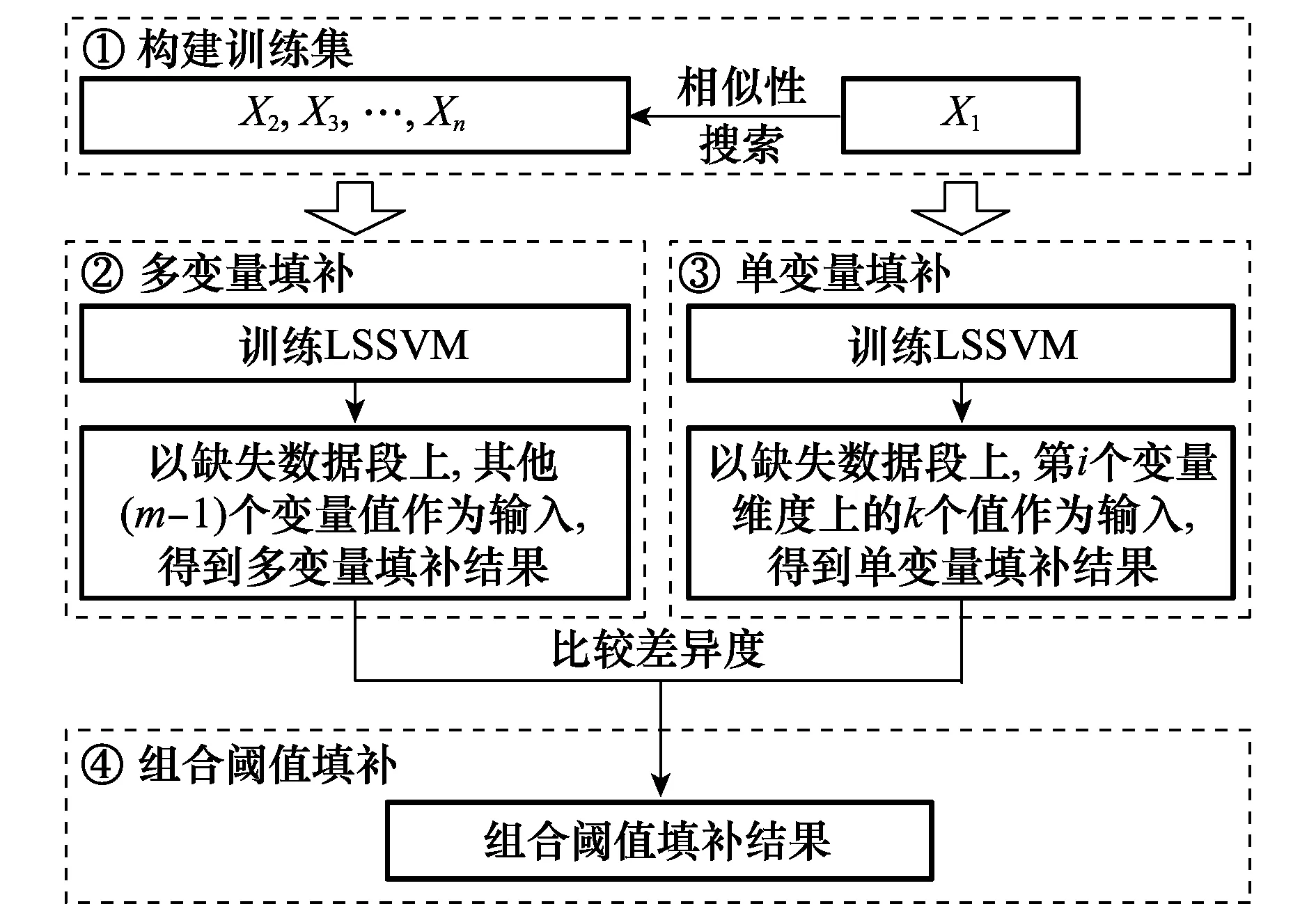
图1 组合阈值填补方法的基本流程Fig.1 Process of the threshold filling method

(1) 构建训练集。在多元时间序列数据集中,搜索与X1相似的其他序列,结果记为X2,X3,…,Xn,构成训练集。

(2) 多变量填补。在X2,X3,…,Xn的每个时刻上,以其他(m-1)个变量维度上的数据作为输入、第i个变量维度上的数据作为输出,训练LSSVM。然后,针对X1的缺失数据段,利用训练后的LSSVM模型进行填补,得到多变量填补结果。

(3) 单变量填补。在训练集的每个序列中,针对第i个变量维度,以k个变量值作为输入,第k+1个变量值作为输出,训练LSSVM。然后,针对X1的缺失数据段,利用训练后的LSSVM模型进行填补,得到单变量填补结果。

(4) 组合阈值填补。以多变量和单变量的填补结果为基础,按照

(6)

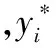
2.3 核函数与参数优化

LSSVM模型中,核函数把样本投影到高维空间,把非线性问题转化为线性问题。由于高斯径向基核函数(radial basis function,RBF)具有良好性能,且只有一个形状参数,因此,文中LSSVM采用RBF核函数。

LSSVM模型涉及2个参数:正则化参数γ和RBF核函数的形状参数σ。γ表示拟合误差权重,γ越大,拟合函数越逼近样本点。σ影响拟合结果平滑程度,σ越大,拟合结果越平滑,但会出现拟合效果不佳的情况;σ过小,拟合结果会出现起伏。为了达到较好的填补效果,应合理选择参数,保证拟合曲线比较平滑,同时具有较小的拟合误差。

3 实验与分析

实验环境为:Intel(R) Core(TM) i7-3770 CPU、4G RAM、Windows 7和Matlab R2010a。

用已知分类结果的公开数据集ASL(Australian sign language)[16]作为实验数据。ASL是一组手语信号,包含22个变量,左、右手动作各用11个变量描述:5个变量表示各手指的弯曲程度;6个变量(6个自由度)表示手的位置。数据集包含95种语意(95个类),每种语意包含27个序列,一共2 565个序列。

不失一般性,分别用前两种语意alive、answer的第27个序列(记为alive_27、answer_27)作为实验对象,序列长度分别为57、54。删除第6个变量维度上的最后10个数据,模拟缺失数据,如图2所示。比较多变量填补、单变量填补、组合权重填补[14]和组合阈值填补等4种方法的填补效果,以平均相对误差e作为比较依据。

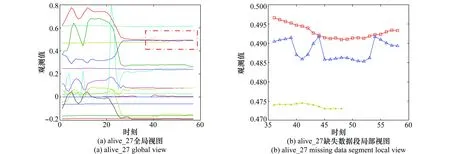
图2 存在缺失数据的alive_27Fig.2 Sequence containing missing data (alive_27)

(7)

式中,n为缺失数据个数;si,ri分别表示第i个填补值和真实值。

3.1 填补效果的比较

为了客观地比较填补效果,4种方法均以相似性搜索[17]的结果作为训练集,本文重点是数据填补,因此直接用与alive_27、answer_27同类的其他26个序列作为相似性搜索结果、构成训练集。

3.1.1 针对alive_27的填补

先对alive_27进行填补,多变量填补γ=2,σ=5时,e达到最小值3.6×10-4。针对不同的步长k,进行单变量填补,遍历γ,σ各种组合,当k=10时,e达到最小值3.3×10-4,对应的γ=38,σ=67。

组合权重、组合阈值填补均以多变量、单变量填补结果为基础,涉及参数分别为权重ω、阈值t。当ω=0.6时,组合权重填补e=3.16×10-4达到最小值。用式(6)计算每个时刻,多变量与单变量填补的差异度,如图3所示。图3(a)为针对alive_27的差异度,在10个填补数据中,时刻50、57上的差异度较大,阈值t=4×10-4时,组合阈值填补用多变量与单变量填补的均值表示两个时刻的填补数据。4种方法的填补结果如图4所示,误差如表1所示。

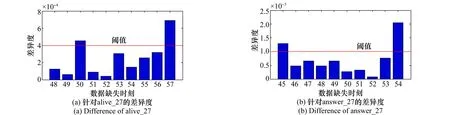
图3 多变量与单变量填补的差异度Fig.3 Difference between the results of multivariate and univariate filling methods

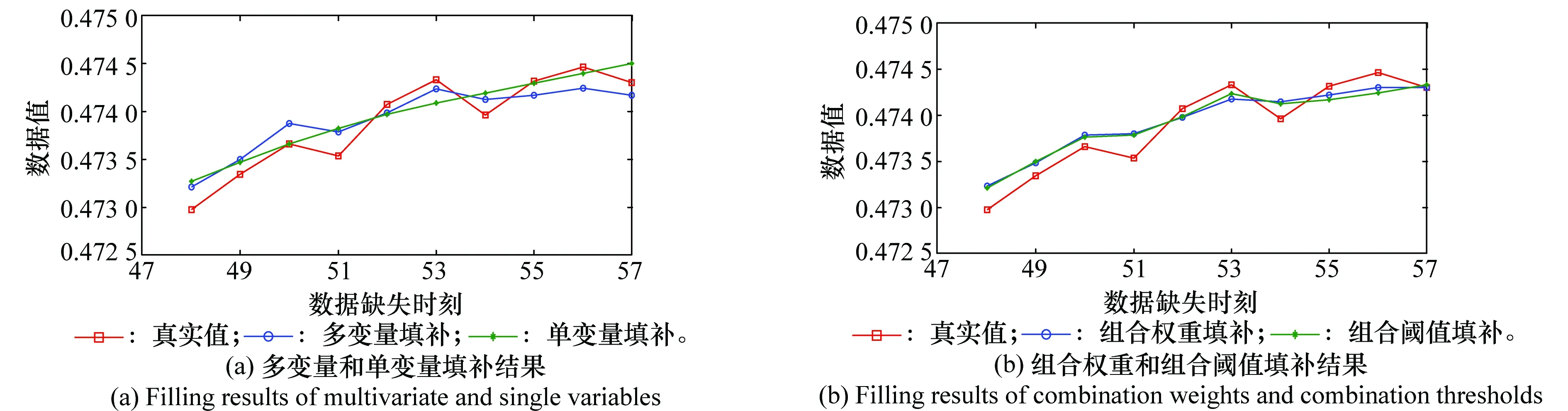
图4 针对alive_27的填补结果Fig.4 Filling results for alive_27

3.1.2 针对answer _27的填补

类似地,对answer_27进行填补,其中,多变量填补γ=38 700、σ=120;单变量填补k=10、γ=130、σ=152;组合权重填补ω=0.6;根据图3(b)针对answer_27的差异度,组合阈值填补t=1×10-3。填补结果如图5所示。

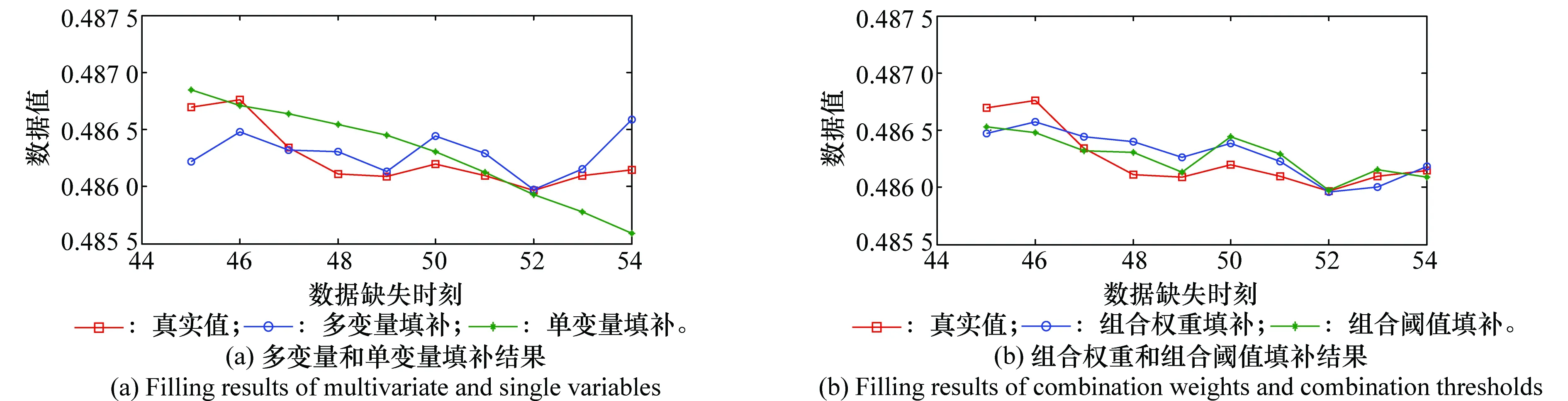
图5 针对answer_27的填补结果Fig.5 Filling results for answer_27

从alive_27、answer_27的填补结果可以看出,单变量填补体现了缺失数据的变化趋势;多变量填补能够体现波动情况。与组合权重方法相比,组合阈值方法确定阈值t,更加明确,且填补误差较小。

3.2 缺失数据段长度对填补的影响

为了进一步比较4种方法的填补效果,增加缺失数据段的长度。分别删除序列alive_27中第6个变量维度上的最后20、30、40个数据。填补结果如图6所示,填补误差如表2所示,对应的参数设置如表3所示。

随着缺失数据段长度的增加,4种方法的填补效果同上文类似,但多变量填补在部分数据段上的填补偏差变大。原因在于,单变量填补方法在缺失数据所属的变量维度上,以k个点为初始值进行填补,能够较好地保持序列趋势;但每次填补都以上次填补的结果作为输入、存在累积误差,难以体现波动细节。多变量填补方法利用其他多个相关变量信息,每次填补都以已知数据作为输入,不存在累积误差,能够体现波动细节;但没有利用缺失数据所属变量信息,在某些点上存在较大偏差。

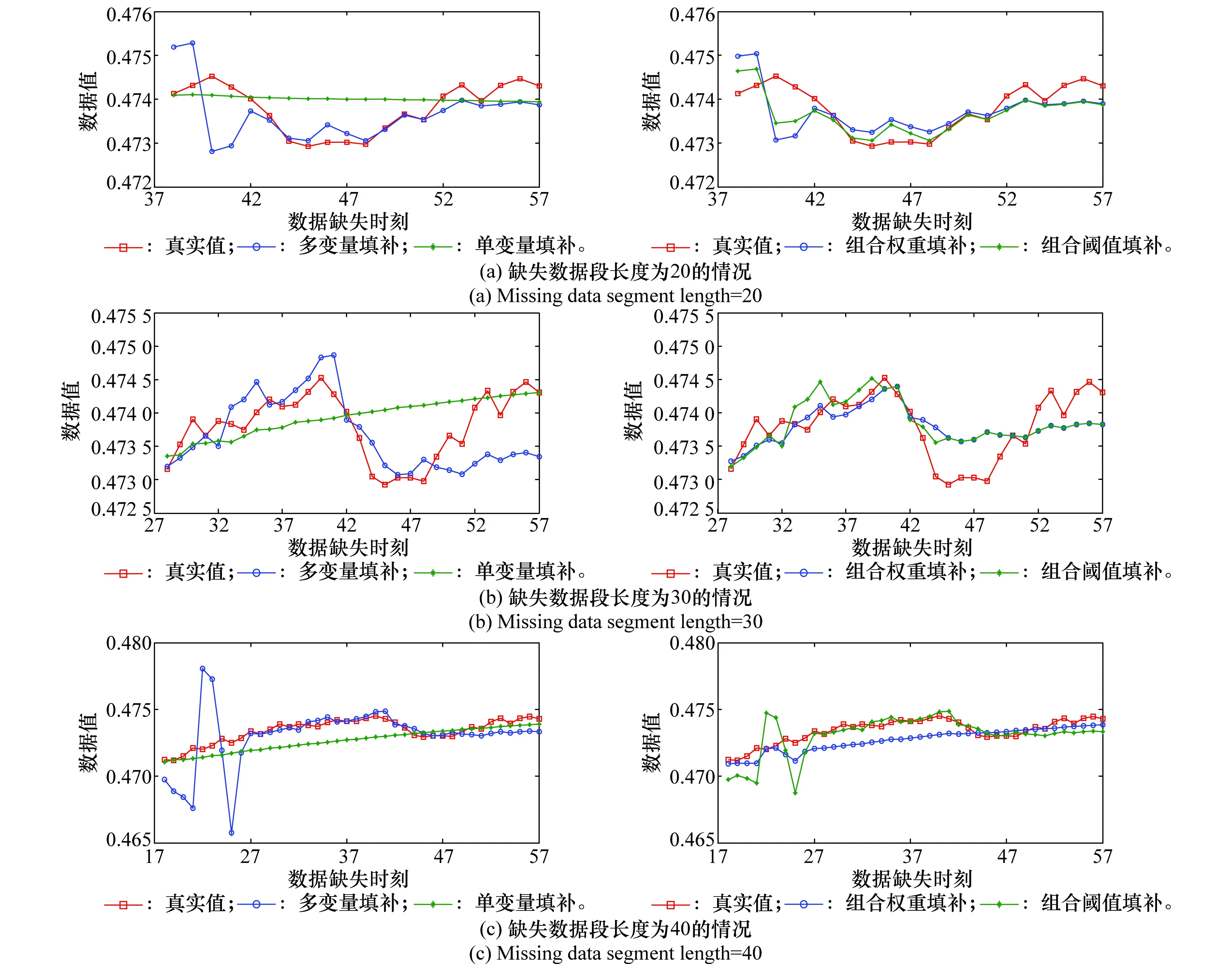
图6 缺失数据段长度对填补效果的影响Fig.6 Relation between the length of missing data segment and its filling effect

表3 4种方法的参数设置

相比之下,组合权重、组合阈值填补的精度较高,受缺失数据段长度的影响不大。这是因为两种方法利用单变量和其他相关多变量信息,较好地体现了波动细节,也有效避免了较大偏差。

然而,组合权重填补对单变量和多变量填补结果加权平均,用一个权重值处理所有的缺失数据,难以体现各个缺失数据的差异性;此外,权重值不易确定也限制了其使用。组合阈值填补以多变量填补结果为基础,当多变量与单变量填补的差异度较大时,以两者的均值作为填补结果,既体现了填补的差异性,也避免了权重值的选择。

4 结 论

在小样本情况下,针对多元时间序列中的缺失数据,利用缺失数据所属单变量和其他相关多变量信息,提出了一种基于LSSVM的组合阈值填补方法,并进行了实验验证。结果表明,它能较好地体现序列的波动细节,且受缺失数据段长度的影响相对较小。

与组合权重填补方法相比,组合阈值填补方法的参数(差异度阈值)较容易确定,且能较好地体现填补的差异性,填补精度较高。

[2] 韩敏, 许美玲, 任伟杰. 多元混沌时间序列的相关状态机预测模型研究[J]. 自动化学报, 2014, 40(5): 822-829.

HAN M, XU M L, REN W J. Research on multivariate chaotic time series prediction using mRSM model[J]. Acta Automatica Sinica, 2014, 40(5): 822-829.

[3] 吴虎胜, 张凤鸣, 张超, 等. 多元时间序列的相似性匹配[J]. 应用科学学报, 2013, 31(6): 643-649.

WU H S, ZHANG F M, ZHANG C, et al. Matching similar patterns for multivariate time series[J]. Journal of applied sciences, 2013, 31(6): 643-649.

[4] PREE H, HERWIG B, GRUBER T, et al. On general purpose time series similarity measures and their use as kernel functions in support vector machines[J]. Information Sciences, 2014, 281(4): 478-495.

[5] LI H L,GUO C H.Piecewise cloud approximation for time series mining[J]. Knowledge-Based Systems, 2011, 24(4): 492-500.

[6] 马茜,谷峪,李芳芳,等.顺序敏感的多源感知数据填补技术[J].软件学报,2016,27(9): 2332-2347.

MA Q, GU Y, LI F F, et al. Order-sensitive missing value imputation technology for multi-source sensory data[J]. Journal of Software, 2016, 27(9): 2332-2347.

[7] 吕政, 赵珺, 刘颖, 等. 基于最大方差权信息系数的煤气数据填补[J]. 控制理论与应用, 2015, 32(5): 646-654.

LÜ Z, ZHAO J, LIU Y, et al. Missing data imputation based on maximal variance weight information coefficient for gas flow in steel industry[J].Control Theory & Applications,2015,32(5):646-654.

[8] 雷春丽, 芮执元. 基于多元自回归模型的电主轴热误差建模与预测[J]. 机械科学与技术, 2012, 31(9): 1526-1529.

LEI C L, RUI Z Y. Thermal error modeling and forecasting based on multivariate autoregressive model for motorized spindle[J].Mechanical Science and Technology for Aerospace Engineering, 2012, 31(9): 1526-1529.

[9] ZOUCAS F A M, BELFIORE P. An empirical analysis of a neural network model for the time series forecasting of different industrial segments[J]. International Journal of Applied Decision Sciences, 2015, 8(3): 261-283.

[10] VAPNIK V. The nature of statistical learning theory[M]. NewYork: Springer-Verlag, 1995.

[11] 许磊, 张凤鸣. 缺失飞参数据填补的组合方法研究[J]. 计算机工程与应用, 2010, 46(21): 210-212.

XU L, ZHANG F M. Research on combined method in missing flight data complement[J]. Computer Engineering and Applications, 2010, 46(21): 210-212.

[12] CHEN T T, LEE S J. A weighted LS-SVM based learning system for time series forecasting[J]. Information Sciences, 2015, 299(C): 99-116.

[13] 谢川,倪世宏,张宗麟.一种缺失飞行参数预处理的新方法[J].计算机仿真,2005,22(4): 27-30.

XIE C, NI S H, ZHANG Z L. A new method for preprocessing in absent flight parameter[J].Computer Simulation,2005,22(4): 27-30.

[14] 杨轲, 张晓丰, 赵录峰, 等. 基于LSSVM的缺失飞行数据组合填补方法[J]. 火力与指挥控制, 2013, 38(1): 84-90.

YANG K, ZHANG X F, ZHAO L F, et al. Combined method of complementing missing flight data based on LSSVM[J]. Fire Control & Command Control, 2013, 38(1): 84-90.

[15] LANGONE R, ALZATE C, KETELAERE B D, et al. LS-SVM based spectral clustering and regression for predicting maintenance of industrial machines[J]. Engineering Applications of Artificial Intelligence, 2015, 37(37): 268-278.

[16] MOHAMMED W K. High-quality recordings of australian sign language signs[EB/OL].[2017-01-20].http :∥kdd.ics.uci.edu/databases/ High-quality Australian Sign Language/ High-quality Australian Sign Language. html.

[17] KEOGH E, RATANAMAHATANAC. Exact indexing of dynamic time warping[J]. Knowledge and Information Systems, 2005, 7(3): 358-386.