基于Nash-Q的网络信息体系对抗仿真技术
闫雪飞, 李新明, 刘 东, 王寿彪
(装备学院复杂电子系统仿真实验室, 北京 101416)
0 引 言
武器装备体系(简称为体系)作战仿真研究一直是军事领域的热点和难点,对于指导体系发展建设[1]、进行使命能力论证[2]、开展系统需求评估、辅助战场指挥决策等均具有重要的意义。网络信息体系(network information system-of-systems,NISoS)被认为是体系发展的高级形态,虽然相关概念才刚提出,但却引起了军事专家的高度重视。目前,针对NISoS的基本概念、内涵和架构研究已形成共识,对其基本形态也有了一个初步的认识,但对其更深层次的作战机理研究则尚未起步,因此,迫切需要开发新的适合探索NISoS特征规律和概念演示的作战仿真平台,对于NISoS的论证评估研究具有基础性意义。
通过总结针对NISoS的相关研究成果,可知NISoS是指由基础网、感知网、决策网、火力网、保障网共同组成的,通过集成各种信息共享网络,将陆、海、空、天、电、网多维战场空间融为一体的大规模武器装备体系。基本架构由基础网、感知网、决策网、火力网、保障网组成,每个子网又由相应类型的武器装备聚合而成,这是与一般武器装备体系的主要区别,如图1所示。另外,其基本内涵为网络中心、信息主导与体系支撑,而如何以网络为中心、以信息为主导、以体系为支撑则是需要进一步研究的内容。NISoS也是一个武器装备体系,因此NISOS是一个复杂巨系统,同时也是一个复杂适应系统,而multi-Agent系统(multi-Agent system,MAS)是复杂系统以及复杂适应系统研究的主要渠道[3-4],此外,NISOS的复杂性、非线性、涌现性等体系特征也特别适合于采用MAS进行探索,因此,基于MAS的建模仿真是NISOS试验研究的最佳选择。但NISoS的极端复杂性则是制约将MAS技术进行成功移植的一大挑战,其中,体系驱动的核心——Agent认知决策技术,则是最关键也是最棘手的环节。
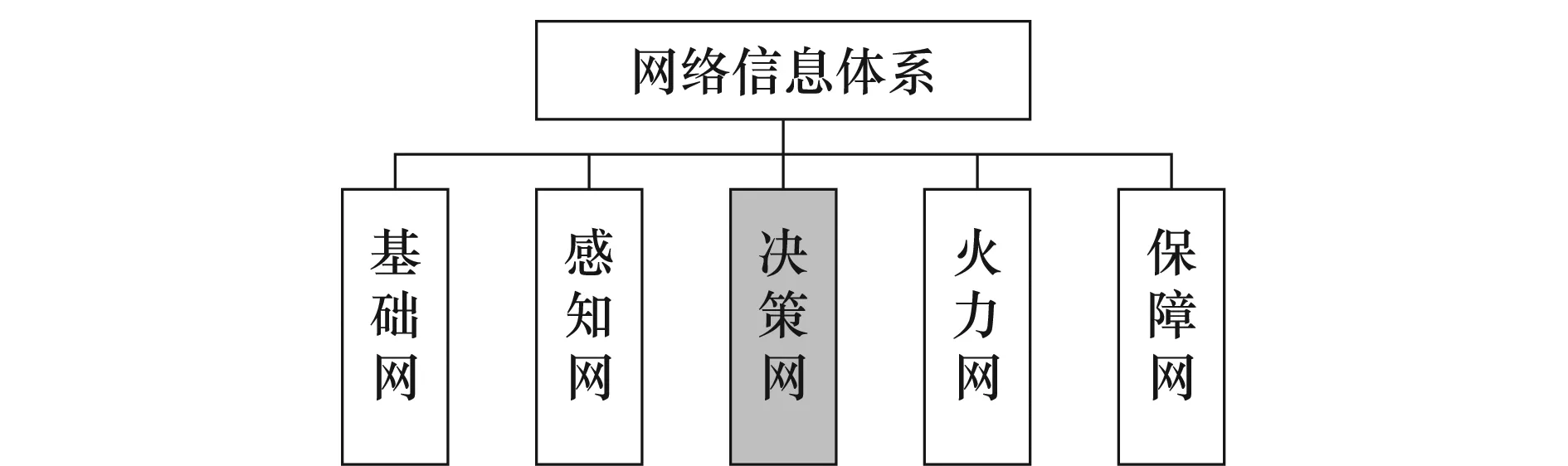
图1 NISoS架构示意图Fig.1 Schematic diagram of NISoS architecture
文献[5]对空战Agent的决策行为进行了理论研究,采用反应型Agent决策,并结合作战实际将Agent的决策规则分成了不同的阶段,包括起飞阶段、巡航阶段、攻击阶段、规避阶段以及降落阶段等。文献[6]在海军作战任务中采用了反应型Agent对指挥官的决策行为进行了建模,并对每条规则的权值进行了设定,具有最大权值的规则被采用,而在实际应用时,规则可以根据实际情况进行更新。文献[7]基于信息、愿望和意图(belief desire intention,BDI)模型对不对称作战Agent的决策制定进行了研究,但由于BDI基于逻辑演绎的推理方式,在实现过程中过于复杂,尤其是对于更复杂的作战场景。文献[8]针对multi-Agent作战仿真决策机制的复杂性、不确定性提出了一种基于组件思想的Agent体系结构——基于multi-Agent的非对称作战仿真体系结构(multi-Agent based asymmetric combat simulation architecture,ACOMSIM),包括逻辑推理Agent、行动制定Agent、地形分析Agent、己方态势感知Agent、敌方态势感知Agent、任务时间调度Agent、任务分析Agent等,通过模块化的思想将复杂问题简单化,各个组件Agent相互协作共同实现问题的求解,其主要不足是各个组件都依赖于丰富的先验知识,且不同组件之间的通信开销降低了决策的效率。上述针对作战Agent的决策行为研究都具有一定的代表性,但仅适用于特定的情形,且都存在一定程度的不足,尤其是当作战体系更复杂、环境的不确定性更高时。
强化学习(reinforcement learning,RL)作为一种无师在线决策技术,在无需任何先验知识的情况下即可实现对未知环境的学习,具有对不确定环境自适应的能力,因此被广泛用于复杂环境包括体系对抗仿真情形下的智能体自主决策研究[9]。文献[10]以战场仿真中安全隐蔽的寻找模型为例,对基于半自治作战Agent的Profit-sharing增强学习进行了实验研究;文献[11]将强化学习引入智能体模糊战术机动决策模型中,有效地解决了马尔可夫决策过程(Markov decision process,MDP)状态转移规律难以获得时的模型求解问题;文献[12]基于强化学习对仿真航空兵的空战机动决策问题进行了研究;文献[13]基于高斯径向基函数(Gauss radial basis function,GRBF)神经网络和Q-leaning算法对飞行器三维空间的隐蔽接敌策略进行了学习研究。
上述研究表明了RL在进行作战仿真认知决策方面的可行性,但对于更复杂的NISoS作战仿真决策,RL算法则具有其局限性。其根本原因是体系对抗中的Agent,其执行每个行为的收益不仅取决于自身的行为,还取决于对手的行为,而对于这一点,RL算法则不能很好地考虑,因此出现收敛较慢甚至决策不够合理等问题。而博弈论则是专门研究决策主体相互作用时的一门学问,尤其是在解决非合作博弈方面具有独特地优势。本文的主要创新工作为①针对体系对抗开展博弈论研究;②建立了战役层次零和动态博弈模型;③基于Nash-Q实现了Nash均衡求解;④通过NISoS作战仿真原型系统验证了算法的可行性以及相比Q-leaning的优势。
1 联合Q-leaning算法
Q-leaning算法是一种模型无关的RL算法,被广泛应用于复杂问题、不确定环境中的Agent认知行为求解。经典Q-learning算法是一种基于单Agent的RL算法,学习的Q值对应于单个Agent的状态-动作对,其优势在于即使只知道每个状态下的立即奖赏值,也可以基于时间差分(temporal difference,TD)公式完成Q(s,a)的学习,即
Qt(s,a)=Qt-1(s,a)+
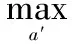
(1)
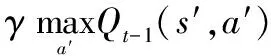
基于单Agent的Q-leaning算法在选择下一个动作时,仅仅考虑自身的行动而不去考虑对手动作的影响,这样做的好处是计算复杂度低并且实现起来容易,但也面临学习结果不够准确的问题,因此,采用联合Q-leaning算法是一种有效的解决途径。相比基于单Agent的Q-leaning算法,联合Q-leaning将原来的状态-动作对Q函数扩展为状态-联合动作对Q函数,即增加了自变量的维数,同样基于TD公式,其Q函数的迭代形式[14]为
(2)
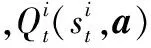
2 Nash-Q算法
Nash-Q算法与联合Q-learning算法类似,都是基于TD公式迭代求解,并且Q函数对应的动作为所有Agent的联合动作,区别在于其策略选取形式。Nash-Q算法基于Nash均衡选择新状态下的联合动作,并且不需要获取其他Agent的历史动作信息,但是需要其他Agent的支付函数以及动作集。对于有两个Agent的博弈模型,设QA为A的支付函数,QB为B的支付函数,则Nash-Q的迭代公式为
(3)

3 问题描述
3.1 作战仿真原型系统及作战想定
为了实现NISoS的作战仿真研究,基于Java语言自主开发了一款作战仿真原型系统。系统采用分布式进程调度架构,采用时间离散方式,通过用户界面可向红蓝双方的对抗体系加入不同类别的Agent,共包含6种类型的Agent,分别为通信Agent(communication Agent,CCAgent)、侦察Agent(scout Agent,SCAgent)、补给Agent(supply Agent,SUAgent)、修复Agent(repair Agent,RPAgent)、打击Agent(attack Agent,ATAgent)以及指控Agent(canmand Agent,CMAgent),对应于NISoS的组成架构,可支持面向NISoS的地空一体化体系对抗研究,如图2所示。

图2 面向NISoS的空地一体化作战仿真情景Fig.2 NISoS oriented ground to air integrated combat simulation scene
需要说明,虽然仿真时构建的NISoS与现实中的NISoS在规模和复杂程度上还有很大差距,但是作为真实NISoS的雏形,研究结果对于真实NISoS的规划设计等相关研究具有一定的启发。原型系统的物理作战空间为按照JAVA3D标准定制的100 m×100 m的三维几何地图,在作战开始时,红蓝双方的兵力被分别自动部署在地图的左右两侧,当仿真开始后,双方会相向运动,直到在中间区域遭遇并展开对抗。
从层次上分,NISoS共包含两个层次:战术层次和战役层次。其中,CCAgent、SCAgent、SUAgent、ATAgent、RPAgent隶属于战术层次,由于其决策行为相对简单,可采用有限状态机实现。而CMAgent隶属于战役层次,负责对所属Agent的指挥与控制,决策行为比较复杂,是论文研究的重点。
3.2 指控Agent的认知域描述
由于系统基于时间离散模型进行调度,因此CMAgent的决策行为是以仿真时钟为单位进行的,其主要目的是在当前感知态势的基础上进行决策,其认知域描述如表1所示,考虑到RPAgent为少量(通常红蓝双方各有一个,作为双方“大后方”出现),忽略其影响。

表1 CMAgent的认知域描述表
此外,CMAgent还能够获取杀伤敌军数目以及死亡数目的实时信息。然而,CMAgent无法获取对手Agent的支付函数以及行为策略,并且对于态势感知也是具有不确定性的,这是体系对抗博弈模型求解的难点。
4 基于Nash-Q的CMAgent认知模型
4.1 参数的规范化
为了压缩参数空间,也为了使学习成果更具一般性,需要首先对用到的学习参数进行规范化,其意义类似于流体力学中的无量纲化,对于实验结果至关重要。主要包括状态空间参数的归一化以及奖赏参数的规约。状态空间的归一化公式为
式中,δ是一个极小值,其意义是避免除零,根据归一化公式,CMAgent的状态空间可由四维参数向量s={NCC,NSC,NSU,NAT}表示。奖赏信息的规约公式为

式中,EK为杀伤敌军数目;OD为死亡友军数目;δ的意义同前。可以看出,当r>0时,CMAgent得到的是正奖赏,当r<0时,CMAgent得到的是负奖赏,奖赏的好坏一目了然。通过以上对学习参数的规范化处理,使得学习数据更具普遍性,并且限定了范围。
4.2 状态空间的分割
传统的Q函数采用表格进行状态空间的离散,然而,当状态空间是连续的且维数较多时,表格离散法会面临“分割难题”,并且学习效率较低。考虑到GRBF神经网络的离散性能以及泛化能力,可以采用GRBF神经网络对Q函数进行离散[12-13]。所谓泛化能力是指即使某个样本没有学习,GRBF神经网络也能估计其输出,而这是表格离散法不能做到的,其网络结构如图3所示。

图3 基于GRBF神经网络的Q离散Fig.3 Q discretization based on GRBF neural network
由图3可知,GRBF神经网络由4层组成,第1层为输入层,第2层为离散层,第3层为隐含层,第4层为输出层。其中,离散层的等宽离散公式为

(4)
可以算出,输入状态空间的样本数目最大为54=625个,可以想象采用传统离散方法的复杂性,其输出层是对应联合动作a={a1,a2,…}的Q值,共有|A|×|A|=3×3=9个联合动作,其计算公式为
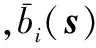
式中,径向基函数bi(s)的计算公式为
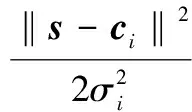
式中,ci是第i个基函数的中心,与s具有相同的维度;σi是第i个基函数的宽度;m是隐含层的个数;‖s-ci‖为输入状态与基函数中心的欧氏距离。
4.3 Nash均衡的计算
定义1(混合策略) 一个Agent的混合策略为其行动空间的一个概率分布为
式中,aij为Agenti对应的第j个行动,下面给出混合策略Nash均衡的定义。
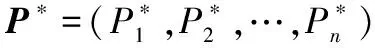
Nash-Q算法采用Q函数代替支付函数,假设学习Agent的支付函数为矩阵Amn,对手Agent的支付矩阵为Bmn,则根据Nash均衡的定义,双方混合策略的求解可转化为线性规划问题,即


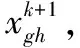
由于任何时刻

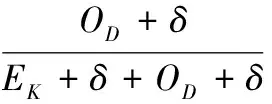
因此QA+QB=0,故CMAgent的博弈模型为零和博弈,故在已知自己的Q函数情况下,对手的支付函数可以设为Q函数的负,至此,可以实现Nash均衡的求解,而求解的Nash均衡对应的Q值即可作为Agent的学习目标,如式(3)所示。
4.4 GRBF网络结构的参数训练

(5)
式中,idx(at)为执行的行动的序号;TDNash为Nash强化信号,其计算公式为
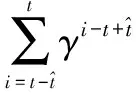
TDNash的计算公式与式(3)是有区别的,即GRBF神经网络的学习目标为Nash均衡而非单一状态-动作对的Q函数。
4.5 学习过程
学习过程以周期计数,当一个回合的作战结束时视为一个学习周期的结束,其学习框架如图4所示。

图4 基于Nash-Q的CMAgent认知学习框架Fig.4 CMAgent cognitive learning framework based on Nash-Q
基于Nash-Q的NISoS战役层次CMAgent的决策过程如下:
步骤1初始化CMAgent的GRBF神经网络,通过k-means聚类设置GRBF的中心和宽度,设定最大学习周期数K,令k=1;



步骤5执行决策at,转到新的状态st+1;
步骤6如果仿真没有分出胜负或者t<最大仿真步数,返回步骤3,否则继续;
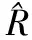
步骤8k=k+1,如果k>K,则结束学习,否则转到步骤2继续。
5 仿真验证
为了对本文所提算法的有效性进行充分验证,在NISoS作战仿真系统中共实现了3种决策方式,第1种是基于Nash-Q算法的决策,第2种是基于Q-Learning算法的决策,第3种是基于规则的决策,通过两两对抗的方式,验证Nash-Q算法的优越性。
5.1 仿真兵力部署
由于实验的目的是为验证基于Nash-Q的指控Agent智能决策算法,因此可以忽略对参战兵力的指标参数进行关注,只研究在相同的兵力结构下,在不同决策算法约束下的体系对抗效果,进而分析决策算法。在地空一体化体系对抗的作战背景下,设置红蓝双方的NISoS结构均相同,且均只有1个编队,对应1个CMAgent,每个编队由5个地基SCAgent、5个空基SCAgent、5个地基ATAgent、5个空基ATAgent、5个地基CCAgent、5个空基CCAgent、5个地基SUAgent、5个空基SUAgent以及1个地基RPAgent组成,由于性能指标不是研究内容,这里省略每种类别Agent的性能指标介绍。
5.2 实验设置

5.3 实验结果分析
5.3.1 Nash-Q与Rule-based算法的对比
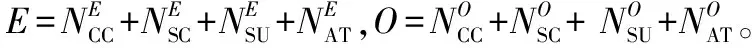

表2 基于Rule-based的CMAgent决策表
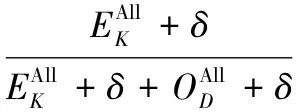

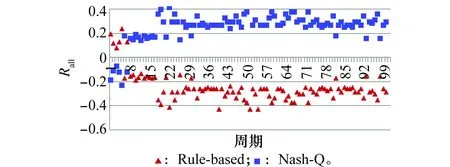
图5 Nash-Q与Rule-based算法的总奖赏值随周期的变化Fig.5 Total reward value of Nash-Q and Rule-based algorithm varying with the period
从图5中可以,看出采用Rule-based的红方在一开始占据优势,这是由于采用Nash-Q的蓝方在初始时刻以探索为主,无任何经验,故在决策上不占优势,然而随着学习周期的增加,Rall快速提升,在20个周期内就已基本收敛。此外,采用Nash-Q算法的蓝方无论是累积奖赏值还是获胜率都要远远高于采用Rule-based决策算法的红方,并且蓝方获胜概率几乎为1,表明了Nash-Q的绝对优势。Nash-Q决策算法能够优于Rule-based决策算法的原因有两个方面,一方面是由于强化学习特有的自适应能力,能够在对抗的过程中逐步掌握对手的弱点并进行相应的针对,另一方面是由于相比Rule-based算法,Nash-Q能够利用更多的态势信息(4个维度共625种),从而能够形成更准确的态势判断。
5.3.2 Nash-Q与Q-learning算法的对比
为了进一步验证Nash-Q算法的学习能力,设计实现了基于Q-learning的CMAgent决策算法,其学习框架同Nash-Q,并且同样采用GRBF神经网络对Q表进行离散,其区别之处在于网络权值的更新,即
由于联合Q-learning需要获取其他CMAgent的历史决策信息,占据通信带宽,且实现起来比较复杂,采用了单Agent Q-learning算法,其中强化信号为


图6 Nash-Q与Q-learning算法的总奖赏值随学习周期的变化Fig.6 Total reward value of Nash-Q and Rule-based algorithm varying with the studying period
5.3.3 Nash-Q的离线决策效能评估
当Nash-Q算法学习到一个较好的GRBF神经网络结构参数后,可以关闭对网络参数的学习,只根据已有的学习成果进行决策,即为离线决策。在离线决策试验中,改变每个阵营编队的数目以制造与在线学习阶段不同的体系对抗情形,并与Rule-based算法进行对比,其中每个编队的配置同前,得到的离线决策效能试验结果如表3所示。其中,Nc代表编队的数目,为了提高运行效率,实验用机的数目不小于Nc,以确保每个CMAgent被分配到单独的节点上。

表3 Nash-Q与Rule-based算法的离线决策效能对比
由表3可以明显看出采用Nash-Q算法的蓝方相比采用Rule-based算法的红方具有与在线决策相当的决策优势,无论是平均总奖赏值还是获胜率都要远远高于红方,表明了离线Nash-Q算法学习成果的普适性,同时也表明了战法战略的通用性,可以作为决策知识库使用。
6 结束语
传统的针对体系作战Agent的认知决策行为主要以BDI推理、反应式为主,主要存在过于依赖专家经验、实现过程复杂以及无法适应动态变化的环境等不足。为此,面向NISoS作战仿真,建立了战役层次指挥Agent不完全信息动态博弈模型,并基于Nash-Q实现了模型求解,可充分发挥强化学习以及博弈论各自的优势,满足对复杂体系对抗环境的自适应学习目的。此外,为了提高模型的泛化能力,采用GRBF神经网络对Q-table进行拟合离散。仿真实验证明了Nash-Q算法的可行性和相比Q-leaning以及反应式决策算法的优越性,并表明了Nash-Q算法较好的离线决策效能。下一步的工作是以动态博弈模型作为红蓝双方的共同决策依据,尽可能去除非理性决策因素对对抗过程的影响,实现体系作战效能的最大化、评估的客观化、决策的智能化。
[1] GILMORE J M. 2015 Assessment of the ballistic missile defense system (BMDS)[R]. Washington, DC: Defense Technical Information Center, 2016.
[2] PATRICK T H, KEVIN M A. Integrated condition assessment for navy system of systems[J]. International Journal of System of Systems Engineering, 2012, 3(3/4): 356-367.
[3] YANG A, ABBASS H A, SARKER R. Landscape dynamics in multi-agent simulation combat systems[J]. Lecture Notes in Computer Science, 2004, 3339: 121-148.
[4] CONNORS C D. Agent-based modeling methodology for analyzing weapons systems[D]. Ohio: Air Force Institute of Technology, 2015.
[5] GISSELQUIST D E. Artificially intelligent air combat simulation agents[D]. Ohio: Air Force Institute of Technology,1994.
[6] ERCETIN A. Operational-level naval planning using agent-based simulation[R]. Monterey: Naval Post-graduate School, 2001.
[7] TSVETOVAT M,ATEK M. Dynamics of agent organizations: application to modeling irregular warfare[J]. Lecture Notes in Computer Science, 2009,5269: 141-153.
[8] CIL I, MALA M. A multi-agent architecture for modelling and simulation of small military unit combat in asymmetric warfare[J]. Expert Systems with Applications, 2010, 37(2): 1331-1343.
[9] GALSTYAN A. Continuous strategy replicator dynamics for multi-agent Q-learning[J]. Autonomous Agents and Multi-Agent Systems, 2013, 26(1): 37-53.
[10] 杨克巍,张少丁,岑凯辉,等.基于半自治agent的profit-sharing增强学习方法研究[J].计算机工程与应用,2007,43(15): 72-95.
YANG K W, ZHANG S D, CEN K H, et al. Research of profit-sharing reinforcement learning method based on semi-autonomous agent[J]. Computer Engineering and Applications, 2007, 43(15): 72-75.
[11] 杨萍, 毕义明, 刘卫东. 基于模糊马尔可夫理论的机动智能体决策模型[J]. 系统工程与电子技术, 2008, 30(3): 511-514.
YANG P, BI Y M, LIU W D. Decision-making model of tactics maneuver agent based on fuzzy Markov decision theory[J]. Systems Engineering and Electronics, 2008, 30(3): 511-514.
[12] 马耀飞, 龚光红, 彭晓源. 基于强化学习的航空兵认知行为模型[J]. 北京航空航天大学学报, 2010, 36(4): 379-383.
MA Y F,GONG G H,PENG X Y.Cognition behavior model for air combat based on reinforcement learning[J]. Journal of Beijing University of Aeronautics and Astronautics,2010,36(4): 379-383.
[13] 徐安,寇英信,于雷,等.基于RBF神经网络的Q学习飞行器隐蔽接敌策略[J].系统工程与电子技术,2012,34(1):97-101.
XU A, KOU Y X, YU L, et al. Stealthy engagement maneuvering strategy with Q-learning based on RBFNN for air vehicles[J]. Systems Engineering and Electronics, 2012, 34(1): 97-101.
[14] 段勇, 徐心和. 基于多智能体强化学习的多机器人协作策略研究[J]. 系统工程理论与实践, 2014, 34(5): 1305-1310.
DUAN Y, XU X H. Research on multi-robot cooperation strategy based on multi-agent reinforcement learning[J]. Systems Engineering-Theory & Practice,2014,34(5):1305-1310.
[15] 贾文生,向淑文,杨剑锋,等.基于免疫粒子群算法的非合作博弈Nash均衡问题求解[J].计算机应用研究,2012,29(1):28-31.
JIA W S, XIANG S W, YANG J F, et al. Solving Nash equilibrium for N-persons non-cooperative game based on immune particle swarm algorithm[J]. Application Research of Computers, 2012, 29(1): 28-31.

