装备保障平台战时运用优化决策分析模型

赵晓东, 李 雄

(陆军装甲兵学院装备指挥与管理系, 北京 100072)

0 引 言

现代战争特别是信息化条件下的战争,参战装备种类多、使用强度高、毁伤方式多元、战损数量大,加上作战节奏快、战场范围广,因此,战场抢修难度大,任务繁重,作用突出。配备一支专业技术强、编制合理的装备保障力量,对于有效遂行战场抢修任务,恢复和保持军队战斗力,具有十分重要的意义。

装备机动保障是装备保障力量机动到达保障地点实施装备保障的方式,是装备保障力量遂行战场保障,特别是担负敌火力打击下装备保障任务的基本方式[1]。由于装备保障力量主要为作战部队提供物资供应保障和装备技术保障,其自身防卫作战能力有限,战斗力较弱,因而搭载保障人员的装备保障平台往往成为敌打击的重点目标。在执行战场抢修任务过程中,由于时间紧迫,战机稍纵即逝,需要根据装备维修任务多少、敌情威胁大小,采取不同的装备保障模式,从而合理调度使用装备保障平台,灵活组织实施战场抢修。若装备保障平台投入不足,战损装备将无法及时修复,不能投入战斗,战斗力再生受到影响;若某一作战方向上投入的装备保障平台过剩,将削弱其他作战方向的保障能力,同时因为保障装备多、目标明显而增大敌方打击的概率。因此,战时如何合理运用并优化配置装备保障平台是装备保障指挥决策的重点内容之一。

文献[2]利用马尔可夫模型建立了考虑转运时间和单级修理情况下的装备维修评估模型。文献[3]在文献[2]的基础上,利用多维马尔可夫链模型建立了基于转运时间和延误时间的装备维修评估模型。文献[4]运用马尔可夫链模型,定量分析了战斗平台的火力运用问题。文献[5]提出了一种改进Theil不等系数的马尔可夫链的导弹备件消耗预测模型。文献[6]构建了基于马尔可夫3级库存系统备件的横向调拨配置模型。上述模型并未涉及装备保障平台在战时运用过程中遭敌打击后的自身状态问题。为此,将利用马尔可夫链对战时装备保障平台在实施机动保障过程中遭遇敌方火力打击后的完好状态进行建模研究。

文献[7-10]建立了装备综合保障能力评估参数,对装备保障力量的综合保障能力进行计算或仿真。文献[11]基于离散系统建模理论,应用Anylogic仿真软件构建了装甲装备维修保障过程仿真模型,并将任务成功性、时效性、经济性作为维修保障资源优化的评价指标,进行了基于指标权重的维修保障资源优化评估。文献[12-13]分别基于通用仿真系统(general purpose simulation system, GPSS)语言和排队理论,构建了装备维修过程的仿真模型,将故障装备的不可用时间最短作为优化目标,对伴随保障力量和定点保障力量的优化配置进行了分析决策。文献[14]通过分析装备保障力量完成任务的能力、机动性和风险性,建立了装备保障力量部署方案的评估指标体系,提出了基于熵权TOPSIS(technique for order preference by similarity to ideal solution)的装备保障力量部署方案优选方法。文献[15]首先对受损目标的保障价值进行了模糊评判,然后运用运筹学目标规划理论,建立了精确调用装备保障力量的数学模型。上述文献虽然研究了装备保障力量的优化配置问题,但大都是基于装备的战损量、维修任务量和任务完成情况来进行研究,没有考虑装备保障平台自身的战损情况。为此,本文综合考虑装备保障平台在战时运用过程中遭敌方火力打击因素,针对装备保障平台自身的战场抢修率最大化而进行的优化编组问题开展决策分析。

1 优化决策分析总体流程

信息化条件下作战,敌各种火力对我装备保障人员、装备、物资和设施的综合毁伤,是战术装备保障力量生存面临的最大威胁。因战斗持续时间短,装备保障平台在作战过程中遂行机动保障任务,不考虑报废,其受到敌方火力打击后,在tn时刻所处状态的概率分布只与tn-1时刻所处的状态有关,而与以前的状态都无关,具有明显的马尔可夫性[16],即无后效性。同理,装备保障平台在条件允许的情况下进行自我维修后,在tn时刻所处状态的概率分布只与tn-1时刻所处的状态有关,而与以前的状态都无关,也具有明显的马尔可夫性。装备保障平台受到敌方火力打击的时间可以用受击次数来表示,从而将其离散化。因此,可以通过构建马尔可夫链模型[17],定量分析装备保障平台的战损问题,以此来判断装备保障平台能否完成战场抢修任务,从而决定其如何配置使用,并进行优化。

在实际作战过程中,有时单作战平台执行一些不太紧迫的任务时,如战术机动、战前侦察等,需配置装备保障单平台进行保障。单平台能否满足保障要求,需要装备保障指挥员进行决策分析:如果能满足需要,则不需要增加装备保障平台个数,既可减小被敌侦察和打击的概率,又可节约保障资源;如果不能满足需要,则需要增加装备保障平台的个数,以完成保障任务。当单作战平台执行重要任务,如冲击突破,或作战分队执行战斗任务时,单平台无法满足战场抢修需要,则需要配置多个装备保障平台进行保障。这时装备保障指挥员需要根据已掌握的敌情和战场抢修效率最高的目标,考虑平台编组的优化问题:2个编为一组(2个平台同时使用),3个编为一组,4个编为一组,或者更多。如果2个编为一组能满足优化条件(战场抢修效率最大),则不考虑3个编为一组,这样可以实现更加灵活的配置,而且避免保障资源的浪费。同理,如果3个编为一组能满足优化条件,则不考虑4个编为一组。通过研究装备保障平台的使用规模与遭敌打击的关系,利用运筹学目标规划理论,构建了基于战场抢修效率最大化的编组优化模型。通过将二者相结合,可以帮助装备保障指挥员对装备保障单平台和平台编组的战时运用进行优化决策分析,具体步骤如图1所示。

2 单平台战时运用模型

装备保障平台在实施机动保障过程中,其状态变化主要来源于遭敌火力打击和自我维修两种基本情况。由于其均具有马尔可夫性,可分别构建装备保障平台受击马尔可夫链模型和维修马尔可夫链模型两种基本模型。然后,根据不同敌情和作战任务,构建无条件自我维修模型和有条件自我维修模型。

2.1 构建状态空间

信息化条件下,嵌入指挥信息系统的装备保障平台在实施战场抢修任务中发挥着核心作用。装备保障平台受到敌方火力打击后,根据指挥信息系统和机械系统的完好程度,可划分为4种状态，表示为

式中,X(t)表示装备保障平台t时刻所处的状态;t表示装备保障平台受敌火力打击时刻对应的受击次数,t=1,2,…,n。

2.2 基础模型构建

2.2.1 受击模型构建

装备保障平台在机动过程中遭遇敌方火力打击后,装备保障平台的状态转移如图2所示。

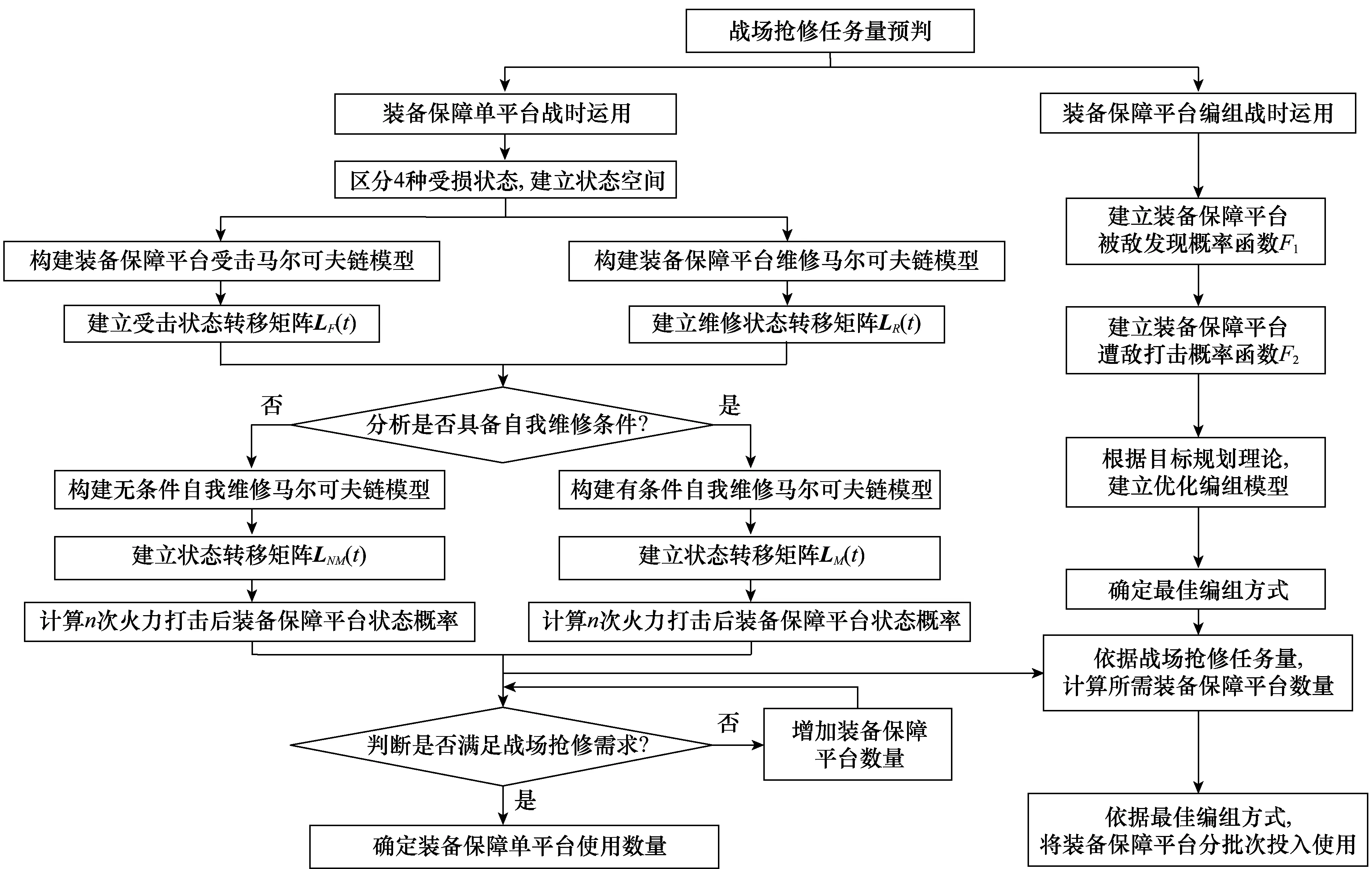
图1 装备保障平台战时运用优化决策分析流程Fig.1 Optimization decision analysis process of equipment support platform wartime application

图2 装备保障平台遭敌打击状态转移图Fig.2 State transition diagram of an equipment support platform after being fire attacked

战前,装备保障指挥员经过统计分析,可得到保障装备战损的历史数据。设装备保障平台指挥信息系统损坏的概率为p1,机械系统损坏的概率为p2,则二者同时损坏的概率为p1p2。因此,图2中有

p01=p23=p1

p02=p13=p2

依据图2可以得到装备保障平台遭敌打击的状态转移矩阵LF(t)，即

(1)

2.2.2 维修模型构建

装备保障平台在机动过程中遭遇敌方火力打击后,如果装备保障平台具备自我维修的条件,可进行自我维修。其自我维修状态转移如图3所示。

图3 装备保障平台自我维修状态转移图Fig.3 State transition diagram of an equipment support platform self-maintenance

战前,装备保障指挥员经过统计分析,可得到保障装备修复的历史数据。设指挥信息系统修复的概率为q1,机械系统修复的概率为q2,则二者同时修复的概率为q1q2。因此，图3中有

p10=p32=q1

p20=p31=q2

依据图3可以得到装备保障平台自我维修的状态转移矩阵LR(t)，即

(2)

2.3 无条件自我维修模型

装备保障平台在机动过程中,遭遇敌方火力打击后,由于军情紧急,时间紧迫,没有时间对受损平台进行自我维修;或者敌情威胁较大,如果不及时转移,会继续遭到敌方更猛烈的火力打击。因此,装备保障平台不具备自我维修条件,需继续机动。这种情况下,装备保障平台的状态转移矩阵LNM(t)等于遭敌打击的状态转移矩阵LF(t),即

LNM(t)=LF(t)

(3)

设装备保障平台的初始状态概率为δ0,则有：

(1) 遭遇敌方1次火力打击后,装备保障平台的状态概率为

δNM1=δ0·LNM(t)=δ0·LF(t)

(2) 遭遇敌方2次火力打击后,装备保障平台的状态概率为

(3) 类似地,遭遇敌方n次火力打击后,装备保障平台的状态概率为

2.4 有条件自我维修模型

在进攻战斗开进阶段,装备保障平台根据上级命令需机动至预定地点,进行定点保障。装备保障平台在机动过程中遭遇敌方火力打击后,由于时间较为宽裕,或者敌情威胁较小,且周围地形适合隐蔽疏散。装备保障平台迅速利用合适地形疏散隐蔽后进行自我维修,待修理完毕后继续机动至预定地域。这种情况下,装备保障平台的状态转移矩阵LM(t)等于遭敌打击的状态转移矩阵LF(t)与自我维修的状态转移矩阵LR(t)的乘积,即

LM(t)=LF(t)·LR(t)

(4)

装备保障平台初始状态概率同上,则有：

(1) 遭遇敌方1次火力打击并维修后,装备保障平台的状态概率为

δM1=δ0·LM(t)=δ0·LF(t)·LR(t)

(2) 遭遇敌方2次火力打击并维修后,装备保障平台的状态概率为

δM2=δM1·LM(t)=δ0·[LF(t)·LR(t)]2

(3) 类似地,遭遇敌方n次火力打击并维修后,装备保障平台的状态概率为

δMn=δM(n-1)·LM(t)=δ0·[LF(t)·LR(t)]n

3 平台编组优化模型

装备维修保障在平时和战时有极大的不同。平时维修的目标是使装备保持和恢复到规定状态,以最低的费用满足战备要求,因此经济性和效益排在第一位;而在战时,由于战机转瞬即逝,战场抢修的目标是使战损装备恢复其基本功能,以最短的时间满足当前的作战要求,因此维修时间和效率则显得尤为重要[18]。战时,装备保障平台想要缩短装备维修时间,提高战场抢修率,可以通过两个途径实现:一是提高装备保障平台的平均维修率;二是增加装备保障平台的数量。第1个途径,一方面需要研制和生产更先进的装备保障设施设备,另一方面需要装备保障人员进行长时间的知识积累和实践磨练,而这两个方面,都需要足够长的时间才能实现,因此不适用于战时。而第2个途径,在装备保障平台平均维修率一定的情况下,通过增加数量来提高战场抢修率,比较简单且容易实现。但由于战时的特殊情况,随着投入战场的装备保障平台数量的增加,规模增大,机动速度放缓,被敌发现的概率和遭敌火力打击的概率也随之增大。因此,装备保障平台在战时的使用数量不能随意增加,而需根据敌情威胁的大小进行优化配置,从而实现装备战场抢修率的最大化。

作战过程中,保障单元投入的保障平台越多,则越易被敌侦察。设装备保障平台被敌发现的概率F1与投入战场数量S成正相关,且

F1=K1(S)·S≤1

同理,投入使用的保障平台越多,则越易被敌攻击。设装备保障平台遭敌打击的概率F2也与投入战场数量S正相关,且

F2=K2(S)·S≤1

式中,K1(S)、K2(S)是S的函数。

设装备保障平台的平均维修率为p,投入战场使用的数量为S,遭敌打击后装备保障平台真正发挥效能的数量为S′,则

S′=S·(1-F1·F2)

装备保障平台的战场抢修率P为

P=p·S′=p·S·(1-F1·F2)=

p·S·[1-K1(S)·K2(S)·S2]

因此,为了实现装备保障平台遭敌打击后战场抢修率最大的目标,根据运筹学目标规划理论,其编组优化模型为

(5)

装备保障平台的平均维修率p与装备保障平台配备的设施设备和操作人员的技能相关,通常,这些因素在持续较短时间的作战过程中可视为常数。因此,装备保障平台的实际维修率P仅与投入战场配置的数量S相关。

4 应用实例

4.1 单平台无条件自我维修应用实例

在一场进攻战斗中,红方一作战平台执行冲击突破任务,遭敌火力打击。根据装备保障指挥所的指示,红方一装备保障平台需快速机动至指定地域进行装备抢修。在机动途中遭遇蓝方的压制性火力打击。由于敌情威胁较大,如果不及时转移,蓝方将加大打击力度,因此,红方装备保障平台不具备自我维修条件,需尽快转移。已知红方装备保障平台指挥信息系统的损伤概率为0.3,机械系统的损伤概率为0.2,二者同时损伤的概率为0.06。

根据式(1),红方装备保障平台受蓝方火力打击后的状态转移矩阵LF(t)为

根据式(3),红方装备保障平台无条件自我维修的状态转移矩阵LNM(t)为

若红方装备保障平台在保障能力齐整情况下投入战场,则其初始状态概率为

遭遇蓝方1次火力打击后,红方装备保障平台的状态概率为

遭遇蓝方2次火力打击后,红方装备保障平台的状态概率为

遭遇蓝方3次火力打击后,红方装备保障平台的状态概率为

红方装备保障平台遭遇蓝方火力打击后,无条件自我维修所处的状态概率分布如图4所示。

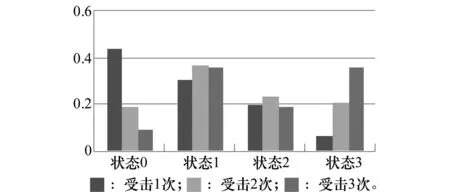
图4 红方保障平台无条件自我维修状态概率图Fig.4 State probability diagram of a red-force equipment support platform in unconditional self-maintenance

由于装备保障单平台对单作战平台进行保障时,目标单一,可以相对容易获取保障对象所处位置;而装备保障平台编组进行保障时,由于所有平台统一行动,部分平台的指挥信息系统损坏,可通过其他平台接收和传递信息;同时,装备保障平台主要担负战场抢修任务,首先需要机动至预定地点,其次需要借助其车载设施设备进行战场抢修。因此,装备保障平台的指挥信息系统损坏对完成保障任务的影响相对较小,将其机械系统的完好程度作为衡量能否完成保障任务的重要因素,即将装备保障平台处于状态0和状态1的概率相加,视为其完成保障任务的概率。

因此,装备保障平台在分别遭遇敌3次打击后,能进行战场抢修任务的概率为:0.74,0.56,0.45。根据军事规则,装备保障平台机械系统完好程度的概率小于0.5,视为无法完成任务,需得到上级加强。由此可见,红方装备保障单平台在不具备自我维修的条件下,遭遇蓝方火力打击3次或以上,将不能完成保障任务,需增加装备保障平台个数。

4.2 单平台有条件自我维修应用实例

某次演习过程中,红方一作战平台执行战场侦察任务发生故障,无法自行排除。红方一装备保障平台根据上级命令,需机动至相关地域进行抢修,在机动途中遭遇蓝方的零星火力打击。由于时间较为宽裕,且周边地形适合隐蔽,红方装备保障平台受击后迅速利用合适地形隐蔽,展开自我维修。已知红方装备保障平台的损伤概率同上,指挥信息系统的修复概率为0.4,机械系统的修复概率为0.3,二者同时修复的概率为0.12。

设红方装备保障平台受蓝方火力打击后的状态转移矩阵LF(t)同第4.1节。

则根据式(2),红方装备保障平台自我维修的状态转移矩阵LR(t)为

因此,根据式(4),红方装备保障平台受蓝方火力打击后有条件自我维修的状态转移矩阵LM(t)为

若红方保障单元刚投入战场时装备齐整,则红方装备保障平台的初始状态概率为

遭遇蓝方1次火力打击并维修后,红方装备保障平台的状态概率为

遭遇蓝方2次火力打击并维修后,红方装备保障平台的状态概率为

遭遇蓝方3次火力打击并维修后,红方装备保障平台的状态概率为

红方装备保障平台遭遇蓝方火力打击后,有条件自我维修所处的状态概率分布如图5所示。

图5 红方保障平台有条件自我维修状态概率图Fig.5 State probability diagram of a red-force equipment support platform in conditional self-maintenance

仍然将装备保障平台处于状态0和状态1的概率相加,视为其能完成保障任务的概率。因此,红方装备保障单平台在具备自我维修条件下分别遭遇敌3次打击后,能进行战场抢修任务的概率为:0.83,0.75,0.72。根据军事规则可见,红方装备保障单平台在具备自我维修的条件下,遭遇蓝方火力打击3次以后,仍能完成保障任务,不需要增加装备保障平台个数。

4.3 平台编组优化应用实例

实例1某次进攻战斗中,红方装备保障平台根据上级命令,需机动至某预定地域对作战部队实施定点保障,根据情报显示,蓝方已派出侦察分队,对红方保障单元进行侦察,并伺机进行火力打击。考虑到信息化作战陆军合成分队战时编组情况,设红方装备保障平台可投入战场配置的数量S∈[0,6],装备保障平台的平均维修率为p=0.8。

设红方装备保障平台被敌发现的概率与投入战场数量成线性正相关,且

(6)

设红方装备保障平台遭敌打击的概率也与投入战场数量成线性正相关,且

(7)

将式(6)、式(7)代入式(5),即可计算出装备保障平台的战场抢修率P。装备保障平台投入战场数量S为自然数,为了更好地观察S′与S的关系,将S看作[0,6]上的连续实数,Matlab仿真结果如图6所示。

图6 保障平台投入战场数量与发挥效能数量关系图Fig.6 Relationship between the number and the effectiveness ofequipment support platforms

实例2在一场对阵地防御之敌进攻战斗中,红方第一梯队作战分队在冲击、扩大突破口时遭到敌疯狂反扑,战损装备急剧增加。根据装备保障指挥所的指示,红方装备保障平台需快速机动至指定地域进行战场抢修。在机动途中遭遇蓝方的压制性火力打击。由于敌情威胁较大,如果不及时转移,蓝方将加大打击力度,因此,红方装备保障平台不具备自我维修条件,需尽快转移。根据第4.1节中的实例,红方装备保障单平台在不具备自我维修条件下分别遭遇敌3次打击后,能进行战场抢修任务的概率为:0.74,0.56,0.45。假设战场抢修需要3个保障单元的抢修能力才能满足需要,则装备保障指挥员可根据掌握的敌情,预测装备保障平台遭敌打击的次数,确定装备保障平台的使用数量,并下定决心:遭敌1次打击,需使用5个保障平台,应配置2个编组和1个装备保障平台分3个批次进行战场抢修;遭敌2次打击,需使用6个保障平台,应配置3个编组分3个批次进行战场抢修;遭敌3次打击,需使用7个保障平台,这时可使用的装备保障平台已不能满足战场抢修需要,应立即请求上级支援。

实例3某次进攻战斗中,红方装备保障平台根据上级命令,需机动至某预定地域对作战部队实施定点保障,在机动途中遭遇蓝方的火力打击。由于时间较为宽裕,且周边地形适合隐蔽,红方装备保障平台在受击后迅速利用合适地形疏散隐蔽,展开自我维修。根据第4.2节中的实例,红方装备保障单平台在具备自我维修条件下分别遭遇敌3次打击后,能进行战场抢修任务的概率为:0.83,0.75,0.72。假设战场抢修需要3个保障单元的抢修能力才能满足需要,则装备保障指挥员可根据掌握的敌情下定决心:遭敌1次打击,需使用4个保障平台,应配置2个编组分2个批次进行战场抢修,修理力量略有浪费;遭敌2次打击,需使用4个保障平台,应配置2个编组分2个批次进行战场抢修;遭敌3次打击,需使用5个保障平台,应配置2个编组和1个装备保障平台分3个批次进行战场抢修。

4.4 结果分析

从图4、图5中可以看出,当红方装备保障平台受击1次以后,其完好状态下降明显;受击2次以后,组织自我维修的装备保障平台的完好率是不维修的2.5倍;受击3次以后,组织自我维修的装备保障平台的完好率是不维修的5倍。经过验证,所建模型与实际作战结果相一致,与军事规律相吻合。这充分说明,装备保障平台受击后,如果条件允许,必须组织自我维修来提高自身完好率;如果条件不允许,不能进行自我维修,必须根据已掌握的敌情去判断受击概率,从而对装备保障平台的战时运用进行决策,才能圆满完成保障任务。

从图6可以看到,在初始阶段,随着红方装备保障平台投入战场数量S的增大,发挥效能数量S′不断提高,战场抢修率P也在不断提高;当S到达某一值后,S′达到极大值,P实现最大化;随后，S′随着S的继续增大而不断较小,当S达到一定值时,S′=0,P=0。这充分说明当红方装备保障平台投入战场数量足够大时,其将成为蓝方攻击的重点目标,从而被彻底消灭,这与军事规律相吻合,符合实际作战结果。因此,装备保障平台在战场上的配置数量不仅要考虑战损装备的维修量,还要根据敌情的威胁大小而进行合理规划,才能实现既提高战场抢修率,又保存装备保障力量的目的。

5 结 论

从信息化条件下装备保障平台在机动保障过程中遭遇敌方火力打击的问题出发,将装备保障平台受打击过程和维修过程描述为系统的有限状态随不同时间阶段不断转移的过程,根据其遭遇打击后面临的不同敌情和战场环境,构建了无条件自我维修和有条件自我维修的马尔可夫链模型,用于装备保障单平台战时运用的决策研究。随着装备保障平台在战场上使用规模的增大,遭受敌打击的概率随之增加,基于战场抢修率的最大化,运用运筹学目标规划理论,构建了编组优化模型,用于装备保障平台优化编组的决策分析。结果表明,基于马尔可夫链的装备保障平台受击预测模型及编组优化模型,具有研究方法简单、运算量小等特点,可以为装备保障力量的作战运用提供决策依据和指导。需要指出的是,在上述建模过程中,为了简化模型,将一次短时间战斗中装备保障平台的受打击损坏率和维修率设为常数,下一步将针对持续较长时间的更大规模的作战,需要考虑损坏率和维修率是随时间变化的函数进行研究,从而提高模型的预测精度。

[1] 蒋跃庆. 军事装备保障[M]. 北京: 中国大百科全书出版社, 2007.

JIANG Y Q. Military equipment support[M]. Beijing: Encyclopedia of China Publishing House, 2007.

[2] YANAGI S, SASAKI M. An approximation method for the pro-blem of a repairable-item inventory system with lateral resupply[J]. IMA Journal of Mathematics Applied in Business and Industry, 1992, 3(4): 305-314.

[3] HARTANTO W, CATTRYSSE D, VAN O D. Inventory pooling of repairable spare parts with non-zero lateral transshipment time and delayed lateral transshipments[J]. European Journal of Operational Research, 2005, 165(1): 207-218.

[4] 李雄, 刘德刚, 丛华. 战斗平台火力运用马尔可夫链模型[J]. 系统工程与电子技术, 2006, 28(10): 1549-1552.

LI X, LIU D G, CONG H. Markov chain model for combat platform fire application[J]. Systems Engineering and Electronics, 2006, 28(10): 1549-1552.

[5] 赵建忠,徐廷学,李海军,等.基于改进THeil不等系数的导弹备件消耗预测[J].系统工程与电子技术,2013,35(8):1681-1686.

ZHAO J Z, XU T X, LI H J, et al. Consumption forecast of missile spare parts based on improved Theil coefficient[J]. Systems Engineering and Electronics, 2013, 35(8): 1681-1686.

[6] 董琪,徐廷学,丛林虎.基于Markov三级库存系统备件横向调拨配置模型[J].系统工程与电子技术,2015,37(11):2524-2530.

DONG Q, XU T X, CONG L H. Allocation model of spare parts for three-echelon inventory system with lateral transshipment based on Markov[J]. Systems Engineering and Electronics, 2015, 37(11): 2524-2530.

[7] GUROV S V, UTKIN L V. The time-dependent availability of repairablem-out-of-nand cold standby systems by arbitrary distributions and repair facilities[J]. Microelectron and Reliability, 1995, 35(11): 1377-1393.

[8] KINSKIE S W. Evaluation of the budget and readiness impacts of battlegroup sparing[D]. Monterey: Naval Postgraduate School, 1998.

[9] SLAY F M, BACHMAN T C, KLINE R C. Optimizing spares support: the aircraft sustainability model[R]. Washington: Logistics Management Institute, 1996.

[10] RAFEA F A. Readiness based decision making: a reactive decision-making model for emergency supply of spare parts in a military scenario[D].Florida:Florida Institute of Technology,2002.

[11] 张会奇, 陈春良, 刘峻岩, 等. 装甲装备维修保障资源优化仿真研究[J]. 系统仿真学报, 2015, 27(1): 142-146.

ZHANG H Q, CHEN C L, LIU J Y, et al. Simulation research on armored equipment maintenance support resource optimization[J].Journal of System Simulation,2015,27(1):142-146.

[12] 曲长征, 王蕾, 赵武奎, 等. 基于仿真的装备维修保障力量配置优化[J]. 指挥控制与仿真, 2013, 35(4): 92-94.

QU C Z, WANG L, ZHAO W K, et al. Equipment maintenance force deployment optimization based on simulation[J]. Command Control & Simulation, 2013, 35(4): 92-94.

[13] 李明, 曲长征, 张波, 等. 基于排队论的战术装备维修力量分配问题研究[J]. 计算机与数字工程, 2011, 39(2): 23-25.

LI M, QU C Z, ZHANG B, et al. Assignment model of tactical maintenance force in wartime based on queuing theory[J]. Computer & Digital Engineering, 2011, 39(2): 23-25.

[14] 周辅疆, 朱小冬, 顾宏余. 信息熵与TOPSIS装备保障力量部署方案优化[J]. 火力与指挥控制, 2011, 36(9): 73-76.

ZHOU F J, ZHU X D, GU H Y. Optimization of equipment support power deployment plan based on information entropy and TOPSIS method[J]. Fire Control & Command Control, 2011, 36(9): 73-76.

[15] 胡亮, 王晖, 霍耀仲. 受损目标保障价值评估与装备保障力量精确调用模型[J]. 火力与指挥控制, 2008, 33(5): 89-92.

HU L, WANG H, HUO Y Z. Support value evaluation of damaged target and accurate selection model of powers for equipment support[J].Fire Control & Command Control,2008,33(5):89-92.

[16] ANDRONOV A. M, VISHNEVSKY V M. Markov-modulated continuous time finite Markov chain as the model of hybrid wireless communication channels operation[J]. Automatic Control and Computer Sciences, 2016, 50(3): 125-132.

[17] PRAGER D, ZHANG Q. Valuation of stock loans under a Markov chain model[J]. Journal of Systems Science and Complexity, 2016, 29(1): 171-186.

[18] 吴跃忠. 装备保障指挥[M]. 北京: 解放军出版社, 2009.

WU Y Z. Equipment support command[M]. Beijing: People’s Liberation Army Publishing House, 2009.