基于雷达方程的AN/TPY-2雷达作用距离与干扰研究

尹 良, 刘红杰, 赵晓峰, 李书芳

(1. 北京邮电大学先进信息网络北京实验室, 北京 100876; 2. 北京未来网络科技高精尖创新中心,北京 100124; 3. 北京电子工程总体研究所, 北京 100854)

0 引 言

2016年,美国和韩国宣布将在韩国部署末段高空区域防御系统,尤其是其配备的雷达探测范围能深入邻国腹地,引发中俄等周边国家强烈不满。其实早在2006年,美国就在日本东北地区部署了一套X波段雷达,主要用于监视朝鲜、俄罗斯和中国的导弹发射活动;2014 年,美国和日本又在日本京都地区部署了第二个X波段雷达,以增强日本和美国本土的弹道导弹防御覆盖[1]。末段高空区域防御系统包含发射器、拦截弹、火控和通信管理系统、X波段地基雷达共4个部分。其中，雷达是由美国雷声公司研制的AN/TPY-2(陆军海军/可搬移雷达监视-模式2)雷达[2],是末段高空区域防御系统的重要组成部分。通过研究AN/TPY-2雷达的作用距离,可以分析其工作性能,并采取针对性的对抗措施,对于巩固我国的战略威慑能力具有一定的意义。

AN/TPY-2雷达包含两种模式:末端模式和前置模式[2]。也就是说,AN/TPY-2雷达具有灵活的任务模式,既可以单个节点独立作为反导系统的火控雷达(末端模式);也可通过前置部署(前置模式),作为弹道导弹防御系统中的一个传感器网络节点,与导弹预警卫星、陆基预警雷达和海基预警雷达等接力预警,形成体系作战。因此,末端模式和前置模式这两种部署模式对AN/TPY-2雷达的作用距离有较大的影响。

(1)末端模式:雷达工作于美国陆军的末段高空区域防御系统中,用于战术反导,是反导武器系统的一部分。与火控中心和拦截器通信,执行探测、跟踪和识别目标的任务,配合反导武器系统担当火控雷达的角色,承担战术任务。

(2)前置模式:主要依靠地理位置优势前置部署提供早期预警,对刚发射的弹道导弹目标进行跟踪与识别,并将数据送往指挥与控制战场管理通信中心。如果目标有威胁,将由地基拦截器或者海基标准系列拦截器进行拦截。因此前置模式执行搜索、辨别和获取目标信息等情报侦察任务,是导弹防御系统的一部分。前置模式的AN/TPY-2雷达需要较远的作用距离,发挥搜索雷达角色,承担战略任务。

所以,AN/TPY-2雷达是一种能够兼顾战术与战略的雷达,不但能够接受系统内部的指令,还能够接受外部指令(例如宙斯盾系统、早期预警卫星、早期预警雷达)。同时,该雷达还可以为宙斯盾、爱国者等系统提供目标指示信息,在美国弹道导弹防御系统中发挥重要作用。另外,AN/TPY-2雷达除了具有灵活的2种工作模式外,还具有相对较小的阵面面积(运输灵活)、工作于X频段(可用频段宽,可以辨别真假弹头目标)、有源相控阵体质(功率大)、快速的波形和频率捷变(抗干扰)等技术特点。因此,AN/TPY-2雷达号称是世界上最大的地面/可机载运输的X波段雷达。未来,AN/TPY-2雷达在美国全球部署的导弹防御系统中将会发挥越来越重要的作用,有必要研究其工作性能以制定有效对抗措施。

分析雷达性能的一个主要的工具是雷达方程,本文主要基于雷达方程对AN/TPY-2雷达系统的最大作用距离进行研究。雷达方程可以给出特定信噪比条件下能够成功探测到目标的最大距离,是评估雷达性能的有力工具。该方程在二战之后由美国海军研究实验室的Norton和Omberg在文献[3]中首次提出,并在工程和学术领域获得了广泛的应用[4-6]。尤其是对于那些将雷达作用距离作为保密参数的国外军用雷达,通过公开发表的部分雷达参数,结合雷达方程就可以近似计算其作用距离。

目前,针对雷达方程的研究较多,专门针对AN/TPY-2雷达系统的雷达方程的研究却很少,甚至针对性干扰的研究还没有。美国康奈尔大学和平与冲突研究所的学者George和Theodore所写的文献[7],是公开发表的第一篇基于雷达方程对AN/TPY-2雷达的作用距离进行研究的文章。但是,文献[7]使用的雷达方程参考的是文献[8],而文献[8]假设的场景是雷达信号的带宽B与脉冲宽度τ的乘积为1。而对于AN/TPY-2雷达这样的X波段宽带雷达(带宽大于100 MHz),由于使用的是脉内调制的可脉冲压缩的线性调频(linear frequency modulation,LFM)波形,文献[7]中Bτ=1的假设并不成立。而且文献[7]在计算雷达方程时,考虑雷达信号的功率而非能量的方法,也违背了雷达方程利用匹配滤波进行信号检测的原理[3],并被雷达专家Barton认为是误用雷达方程的一个典型例子[6]。

因此,本文根据实际的AN/TPY-2雷达参数(主要来自公开文献)进行了雷达方程的推导,得到了不同信噪比条件下雷达的最大作用距离。同时,基于雷达方程的系统级链路仿真平台研究较少,本文通过SystemVue软件搭建了AN/TPY-2雷达的雷达方程链路验证平台,通过该平台完成了理论与仿真的结合,对于雷达总体设计有一定的意义。最后,在SystemVue软件平台上仿真了使用电子干扰的对抗方式降低AN/TPY-2雷达工作性能的可行性。

需要指出的是,本文只是使用了AN/TPY-2雷达的部分公开参数,并忽略了部分因素(例如大气衰减、系统匹配等),所以得到的距离值只是定性的估算。未来可以通过电子情报系统侦测其信号参数,获得更准确的雷达参数信息,以更精确地计算雷达作用距离。

1 AN/TPY-2雷达的雷达方程

1.1 雷达参数

对于AN/TPY-2雷达的技术参数,目前没有官方的公开文献进行雷达全部工作参数的报道,尤其是对于频点、脉冲宽度τ、脉冲重复间隔tr、信号带宽B、脉冲累积个数nf等对于雷达方程较为重要的参数。本文主要参考文献[1,7,9-12]中的数据,进行雷达方程推导过程中的参数计算,所用到的雷达参数如表1所示。需要指出的是,对于不同的雷达参数,会得到不同的计算结果,但是计算方法是一致的。

表1 AN/TPY-2雷达的参数

通过表1的数据可以发现,AN/TPY-2雷达信号采用LFM波形,解决了功率增益与距离分辨率之间的矛盾。另外,得益于X波段具有的大带宽(不小于100 MHz),该雷达能够提供真假目标分辨能力(较容易区分真假弹头)。而美国其他的X波段雷达(陆基X波段雷达和海基X波段雷达)虽然功率更大,但是由于体积巨大,运输不方便,不能灵活运输部署。所以,AN/TPY-2雷达是美国目前唯一具备灵活运输部署能力,且能够辨别真假弹道导弹目标的战略预警雷达。根据雷声公司的宣传资料,该雷达从2005年起,参与了超过50次弹道导弹飞行实验,以及超过数千次的卫星跟踪实验[2]。从文献[2]中“可以跟踪卫星”的表述,可以看出该雷达具有较远的作用距离。由于具体的最大作用距离数值一直没有公开,所以本文基于雷达方程,利用表1的数据推导其最大作用距离。

1.2 最大作用距离

当AN/TPY-2雷达使用单个脉冲进行目标探测的时候,假设采用匹配滤波作为接收机信号检测算法[6],在接收机输出端能够获得的最大信噪比为

(1)

式中,(S/N)max表示能够获得的最大信噪比;E1表示单个脉冲回波信号的能量,单位J;N0表示噪声的功率谱密度,单位为W/Hz;Pt表示发射机的峰值功率,单位为W;τ表示脉冲宽度,单位为s;Gt和Gr分别表示发射天线和接收天线的增益;λ表示波长;σ表示目标的雷达散射截面积RCS,单位为m2;Fp、Ft和Fr分别表示发射接收极化失配因子、发射的方向图传播因子和接收的方向图传播因子;k是玻尔兹曼常数,k=1.38e-23J/K;Ts表示系统噪声温度,单位为K;R表示雷达作用距离;Lt和Lα分别表示发射馈线损耗和大气吸收损耗。假设在AN/TPY-2雷达观察时间t0期间共有n个脉冲,接收时候采用相干脉冲串做为雷达接收机的匹配滤波器,则得到的最大信噪比为

(2)

式中,Ei(n) 是n个脉冲的累积效率,理想情况等于1。考虑到Ptτ=Pavtr,其中Pav表示平均功率,tr表示脉冲重复间隔,式(2)可以写为

(3)

式中，相干累积时间tf=n×tr。将距离变量R放在方程的左边就得到了式(4)所示的雷达方程。

(4)

考虑到Pavtf=ETx,所以雷达的一个相干处理周期上的总发射能量ETx决定了雷达最大作用距离[13],而不是单个脉冲的峰值功率。文献[14]也提出雷达方程中使用能量而非功率的优点之一是:适用于各种复杂的脉压信号,而非仅仅是未调制信号。

(5)

1.2.1 在整个观测时间t0上的相干累积

在整个观测时间上相干累积(t0=tf),则雷达方程(5)可以写为

(6)

1.2.2 在整个观测时间t0上的非相干累积

在相干处理间隔上累积时间为tf,并且在t0上非相干累积,则雷达方程(5)可以写为

(7)

式中,n′=t0/tf,表示用于后续非相干累积的相干处理器的输出端数目；Dx(n′) 表示向n′个非相干累积器馈电的接收机输出端的每个脉冲的信号检测要求。

1.3 前置模式的搜索雷达作用距离

根据AN/TPY-2雷达的两个工作模式可以发现,其处于前置模式时的作用距离远,因此下面主要对该模式进行研究。当处于前置模式时,雷达处于搜索模式,如图1所示。

图1 搜索模式下的雷达方程Fig.1 Radar equation for search mode

假设俯仰搜索方向所要覆盖的角度为Ω,单个波束的俯仰宽度为Ω0,单个波束的驻留时间为t0,单个波束内脉冲累积时间为tf,为了简化，假设t0=tf,当天线完成一定角度Ω0的扫描,雷达就可以得到目标的一批共n个主瓣脉冲的回波样本(回波的脉冲重复频率为fp=1/tr)。则重访时间(也叫搜索时间)ts可以表示为

(8)

(9)

在本文后续公式推导中,称式(9)得到的距离为基准距离。

分析式(9)可以发现,雷达搜索任务的不同决定了其最大作用距离的不同。如果所有的阵元都用于跟踪同一个目标(此时Pav最大),则作用距离最远;如果雷达同时要跟踪多个目标,每个目标上获得的功率值Pav变小,则雷达的最大作用距离将减少。

假设雷达单个波束的宽度Ω0为2°,则覆盖俯仰上±53°总共需要的重访时间为

(10)

如果在一定的角度内同时监视N个目标,仍然要求在给定的重访时间ts时间内完成对N个目标的监视,则每个目标的驻留时间为原来的1/N,则最大作用距离可以表示为

(11)

这也意味着雷达的最大作用距离变为基准距离(见式(9))的(1/N)1/4。但是,图1的雷达搜索模式导致空域过大时,连续两次搜索照射的时间间隔过长,若限定固定的重访时间,则根据式(11)得到的雷达最大作用距离下降。

1.3.1 同时多波束时的雷达方程

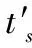
(12)

如果仍然要求在给定的重访时间ts时间内完成对俯仰方向角度Ω的监视,使用M个同时多波束覆盖对应空域的N个目标,则每个目标的驻留时间为原来的M倍,此时的雷达方程可以表示为

(13)

此时,雷达的最大作用距离为基准距离(见式(9))的(M/N)1/4倍,相控阵雷达工作在增程工作模式,其实质是当重访时间固定时,搜索波位变少,则每个波位上允许的波束驻留时间越长、驻留数目越多,则作用距离越远。实际上,从雷达方程(4)中决定雷达作用距离的是雷达发射波形的能量可以看出,同时多波束使得发射机在一个重复周期内同时产生覆盖多个方向的发射波束,必然导致能量的增加,因而相比基准距离(见式(9))也带来了测量距离的增加。

同时，多波束能够解决数据率与目标容量之间的矛盾,尤其是如果空域过大,会导致波位数目过多,会对相控阵带来复杂性的提升。目前,现代雷达常采用搜索屏技术进行监视空域的划分与波位编排。考虑到前置模式部署的弹道导弹目标上升段体积大,且发射后必然穿越事先设置的、由若干重叠的波位组成的搜索屏[17],雷达可以采用“守株待兔”的空域监视方式搜索目标。搜索屏的厚度关系到目标的穿屏时间,进而影响数据率。如果搜索时间ts固定,使用搜索屏导致搜索波位变少,则作用距离变远(因为每个波位上允许的波束驻留数目变多,作用效果类似于同时多波束),也能达到相控阵雷达增程工作的模式。

1.3.2 多帧参差脉冲解距离模糊时的雷达方程

当脉冲重复频率很高时,对应一个发射脉冲产生的回波可能要经过几个周期以后才能被接收到。由于目标回波的延迟时间大于脉冲重复周期,使得收发脉冲之间的对应关系发生混乱,同一个距离读数可能对应几个目标真实距离的现象叫做测距模糊。雷达采用高的脉冲重复频率fr时,在速度上不模糊但会产生距离模糊。解距离模糊的方法主要是利用多帧参差脉冲,通过改变脉冲重复频率(pulse recurrence frenquency,PRF),对发射信号进行脉冲参差,连续或者部分地改变PRF,主要包括连续变化的PRF和多重PRF组[18]。例如,使用几个不同的PRF信号测距,首先顺序使用各个PRF测出对应的模糊距离,再将这些测量值加以比较或者计算,得到无模糊的真实距离。具体的解模糊方法有重合法、余数定理法[19]、相关法和余差查表法等[20]。但是,利用多个PRF解决距离模糊的时候,由于需要做几帧探测才能完成一次距离的测定,因此导致脉冲积累时间tf变短(相比较不需要解距离模糊的场景),根据雷达方程(4),这必然将降低雷达的最大作用距离。

如果在一定的角度内同时监视N个目标,仍然要求在给定的重访时间ts内完成对N个目标的监视。必须将天线扫过目标的时间划分为几段,以适应测距系统所需的多次观测的要求,由于m帧参差处理导致天线扫过每个目标的时间变为原来的1/m,则每个目标的驻留时间为原来的1/(N×m),根据式(9),则最大作用距离可以表示为

(14)

这也意味着雷达的最大作用距离变为基准距离(见式(9))的(1/(N×m))1/4。

经过上面的分析,可以发现不同条件下,雷达的作用距离有不同的结果,如表2所示。

表2 各种条件对雷达最大作用距离的影响

2 雷达方程的数值结果

根据第1节的雷达方程(5)与表1,对雷达接收机输出的最小输出信噪比与雷达的最大作用距离进行计算。为了简化计算,把雷达方程(5)中的脉冲累积效率因子Ei(n)设置为0.8;衰减和损耗因子(Fp,Ft,Fr,Lt,Lα)都设置为1。需要指出的是,如果是要精确地评估雷达的作用距离,则上述衰减和损耗因子不能简单地设置为1,因为这些因子都与距离有着复杂的依赖关系(如此就很难得到距离的闭式解,需要用到计算机迭代编程和图形的方法[6])。

2.1 最大作用距离数值结果

2.1.1 前置模式

根据式(5),假设目标的雷达散射截面积(radar cross section,RCS)取值分别为0.01 m2,0.1 m2,1 m2,10 m2。考虑到洲际弹道导弹在上升阶段的RCS值较大,有利于雷达的信号检测,因此前置模式时考虑RCS=10 m2的情况较符合实际情况。图2的纵坐标表示雷达的最大作用距离(单位为km),横坐标表示接收机所需要的最小信噪比(单位为比值,非dB),脉冲累积个数nf=32。跟据图2可以看出,对于RCS=10 m2的目标,在接收机所需的最小信噪比为5的情况下,AN/TPY-2雷达的最大作用距离是3 735 km,这个距离可以探测到中国东北、华北、江南等地区的弹道导弹发射情况,能够为美国的导弹防御系统提供较长的早期预警时间,对中国的战略威慑能力造成一定的损害。

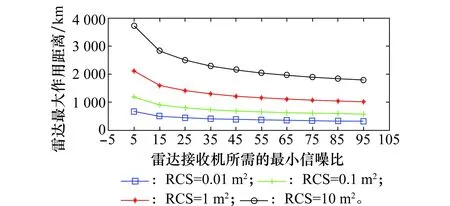
图2 前置模式下的雷达作用距离与信噪比关系Fig.2 Range versus signal-to-noise ratio (SNR) at forward-based mode (FBM)

若表1中的部分参数发生改变,如雷达接收机所需要的最小信噪比还可以更低(如信噪比远小于5),或者脉冲累积个数nf超过32,或者雷达发射功率变大,AN/TPY-2雷达的作用距离还会增大,但是计算方法是一致的。

2.1.2 末端模式

图3是末端模式下的雷达方程数值结果,相比较于前置模式,主要调整的两个参数是目标的RCS和脉冲累积个数nf。由于弹道导弹再入大气层时候,末端阶段的弹头RCS面积小,这里考虑的RCS分别取值0.001 m2,0.01 m2,0.03 m2,0.1 m2;并且假设火控雷达需要同时对付多批次目标,使得脉冲累积个数nf由前置模式的32减少为末端模式的8。所以,图3的末端模式,在最小信噪比为5,RCS为0.1 m2的条件下,雷达的最大作用距离约为834 km。

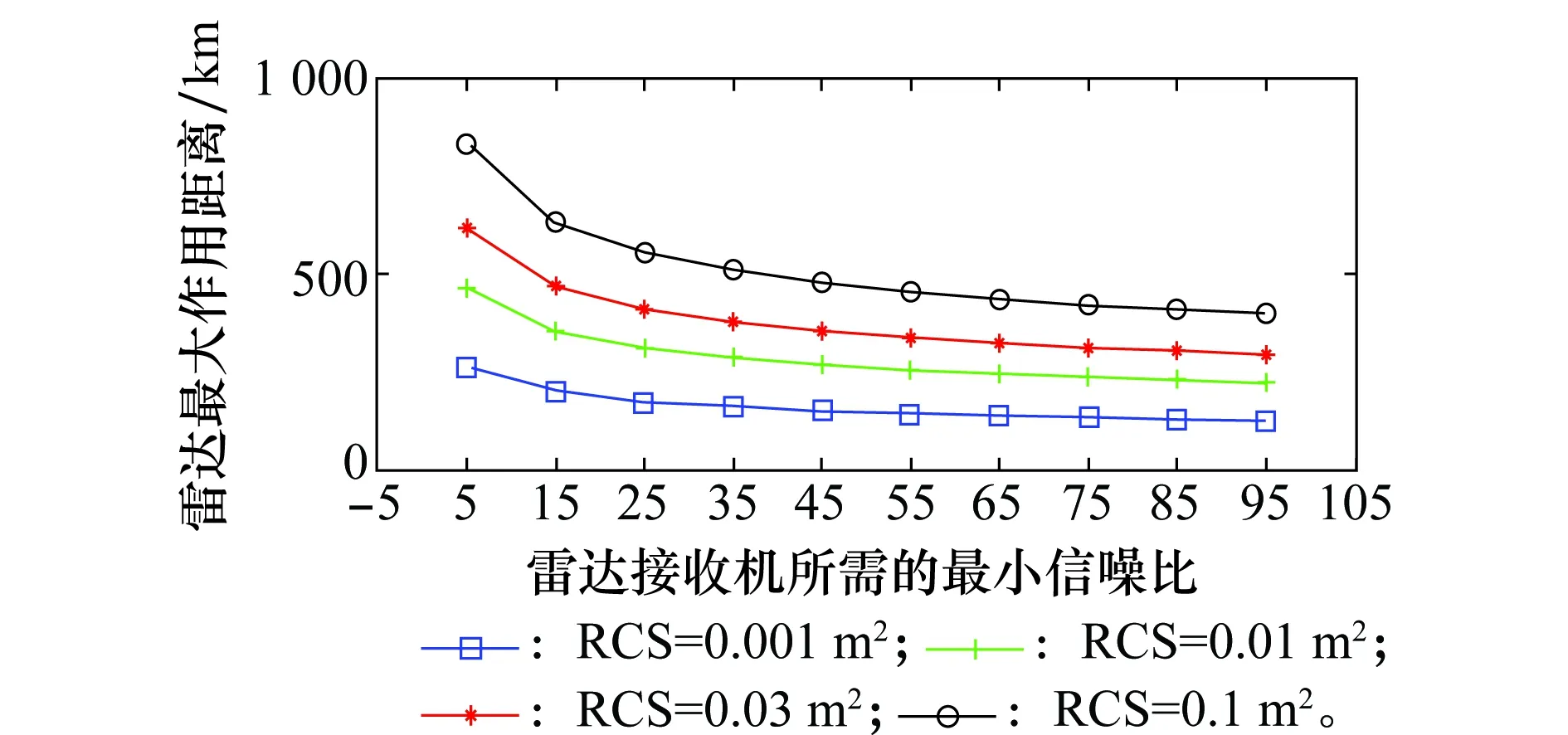
图3 末端模式下的雷达作用距离与信噪比关系Fig.3 Range versus SNR at terminal mode (TBM)

经过上述两种模式的对比可以发现,前置模式雷达作用距离远,可以提供弹道导弹发射的早期预警。针对前置模式对我国战略威慑能力影响较大的特点,下面主要针对该模式进行研究。

2.2 前置搜索模式下的作用距离

搜索模式的雷达方程与第2.1节的区别在于,需要考虑单目标和多目标时,式(9)中目标的重访时间参数ts。

图4表示在俯仰上存在单个目标时的雷达最大作用距离与接收机所需最小信噪比的关系,脉冲累积个数nf=32。结果可以发现,当进行搜索的时候,雷达的作用距离明显降低。对于RCS=10 m2的目标,在接收机所需的最小信噪比是5的情况下,雷达的最大作用距离是1 717 km,小于图2中不搜索情况下的3 573 km。

针对搜索时,雷达的最大作用距离降低,通过提高脉冲累积个数可以进行补偿。如图5所示,当进行搜索的时候,对于RCS=10 m2的目标,在接收机所需的最小信噪比是5的情况下,通过使脉冲累积个数nf从32提高到256,雷达的作用距离也明显得到提高(从1 717 km提高到2 888 km)。

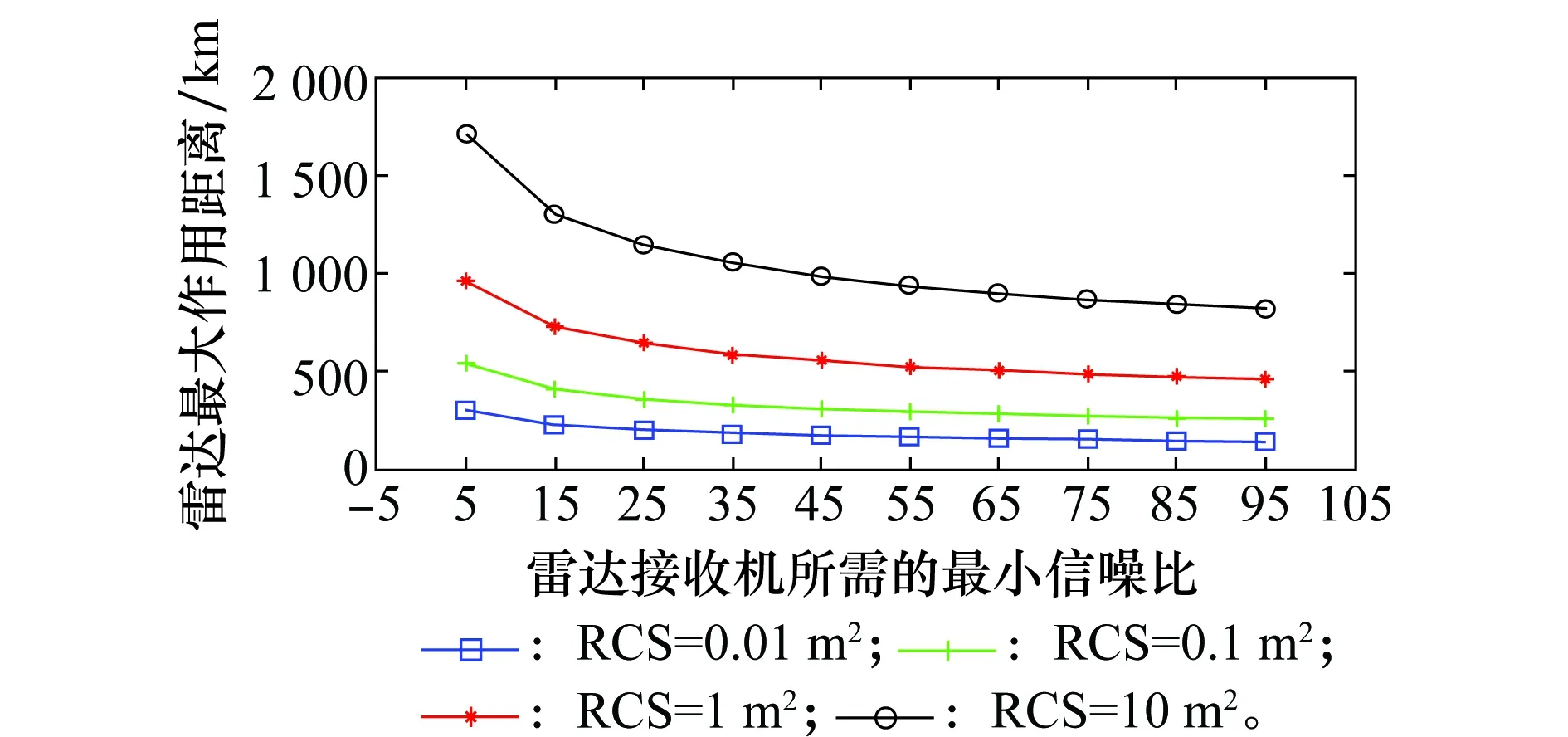
图4 前置模式俯仰单目标搜索Fig.4 Single target elevation search at FBM

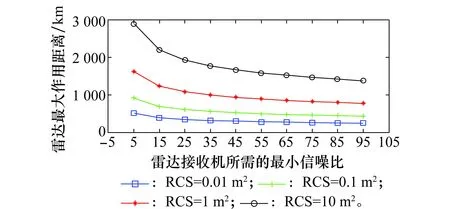
图5 前置模式俯仰单目标搜索(提高脉冲累积数)Fig.5 Single target elevation search at FBM (with increased pulse integration number)

当进行多目标(假设目标个数N=10)搜索的时候,如果仍然要求在给定的重访时间ts内完成对10个目标的监视,则每个目标的驻留时间为原来的1/10。如图6所示,对于RCS=10 m2的目标,在接收机所需的最小信噪比为5的情况下,如果仍然设置脉冲累积个数nf=32,雷达的作用距离也明显降低(965.6 km)。

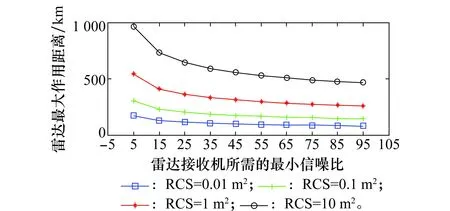
图6 前置模式俯仰多目标搜索Fig.6 Multi target elevation search at FBM

2.3 同时多波束时的作用距离

根据式(13),图7计算了20个同时多波束条件下的雷达最大作用距离,目标个数N=10,脉冲累积个数nf=32。对比图6可以发现,雷达的作用距离从没有使用同时多波束的965.6 km增加到2 042 km。因此,同时多波束技术能够明显提高雷达的作用距离,根据能量角度的雷达方程,本质上是因为发射机在一个重复周期内同时产生覆盖多个方向的发射波束,增加了发射波形的能量,导致最大作用距离增加。

图7 同时多波束明显提高雷达作用距离Fig.7 Multi-beam can improve radar range apparently

2.4 多帧参差脉冲解距离模糊时的作用距离

根据式(14),图8计算了使用3帧参差处理解距离模糊时的雷达最大作用距离,目标个数N=10,脉冲累积个数nf=32。可以发现对比图6,雷达的作用距离从没有使用多帧参差的965.6 km降低到733.7 km。因为多帧参差解距离模糊导致脉冲累积时间减少,导致雷达最大作用距离降低。

从上述图4～图8数值结果可以发现,在没有干扰的条件下,雷达的作用距离主要取决于作战任务的类型。而不同的作战任务会影响目标RCS、目标的数量、脉冲累积个数、搜索空域、同时多波束、距离模糊等参数,使得AN/TPY-2雷达具有不同的最大作用距离。对于干扰方来说,可以通过影响上述参数,来降低雷达的最大作用距离。另外,上述雷达方程推导过程中的系统性能主要受白噪声干扰的影响,实际中可以通过人为施加干扰源的方法,使得干扰信号的功率远远超过白噪声的功率,并超过雷达接收机检测目标的要求,就可以降低雷达的最大作用距离。第3节将基于SystemVue仿真平台研究有干扰条件下的AN/TPY-2雷达的雷达方程。

图8 多帧(3帧)参差处理解距离模糊导致雷达作用距离降低Fig.8 Radar range decrease due to multi-PRF (3 frames) based range ambiguity resolving

3 SystemVue仿真模块设计

SystemVue软件是系统级信号处理仿真平台,可以对雷达、电子战、蜂窝通信、导航等通信系统的物理层进行设计和仿真,对射频、DSP 和 FPGA/ASIC 等部分进行单独或者联合的设计和仿真。对于雷达的总体工程设计,可以使用SystemVue研究不同参数配置下的雷达方程,其包含的模块涵盖了雷达方程需要研究的大部分元素,还可以通过与Matlab的联合编程扩充算法库。如图9所示,仿真系统主要由AN/TPY-2雷达收发链路系统和干扰机系统两个系统组成。

图9 基于SystemVue的AN/TPY-2雷达方程仿真Fig.9 AN/TPY-2 radar range simulation based on SystemVue

3.1 雷达收发链路系统

如图9上半部分所示,通过模块化部件搭建一个完整的反映AN/TPY-2雷达参数的链路,并进行雷达方程验证。其中雷达方程涉及的参数包含:信号波形(脉冲宽度、脉冲重复间隔、LFM)、载频、发射功率、天线增益、目标(目标类型、RCS大小、距离)、接收天线增益、接收机匹配滤波算法、脉冲累积个数、检测要求(检测概率、虚警概率、检测门限)等,按照表1中的参数设置对应的SystemVue模块中的数值。

通过图9可以发现,雷达的收发链路主要包含3部分:发射机、目标、接收机。

(1) 发射机

基带LFM信号通过射频调制,调制到10 GHz的X波段,在基带雷达信号源LFM模块设置带宽为100 MHz;由于射频调制默认的功率是10 mW,需要在后面加上一个放大器,用于保证雷达发射机的平均功率Pav达到AN/TPY-2雷达要求的81 kW(见表1),根据占空比应用公式

(15)

表3 SystemVue中功率计测得的雷达发射功率

(2) 目标

图9中目标模块可以设置距离、速度、目标RCS的统计类型、RCS大小等。表1中的目标参数在这里进行设置。仿真中设置目标RCS的统计类型是Swerling 0型。经过上述设置的雷达回波信号如图10所示,显示了经过10 km距离延迟的2个LFM回波信号。

图10 雷达回波信号Fig.10 Radar echo signal

(3) 接收机

如图9中右半部分所示,回波信号与干扰机的信号合路后首先经过接收天线,接收天线的设置同发射天线。接收天线后面是一个噪声模块,可以对接收机信噪比的大小进行设置。接收机前端完成自动增益控制的设置。接收机信号处理部分完成基于匹配滤波的脉冲压缩、动目标显示、动目标检测、恒虚警率、检测概率Pd计算等功能。

3.2 干扰机模块

由于存在外部干扰的条件下,接收机内部的噪声功率远低于外部干扰,所以可以忽略内部噪声。此时,雷达的系统性能主要取决于干扰机的功率,干扰机位于图9的左下部分,干扰信号可以是录制的基带IQ文件,也可以是噪声干扰信号。干扰机与雷达交互主要通过信干比(signal-to-interference ratio,SIR)的值来设定干扰机的功率。通过观察接收机处于一定干扰下的检测概率值,可以获得有干扰时的雷达性能。

3.3 存在干扰时的雷达性能仿真结果

根据表1的数据,对AN/TPY-2雷达在存在干扰时的工作性能进行仿真,如果如图11所示。目标距离是1 000 km时,RCS类型为Swerling 0,RCS=1 m2,恒虚警概率设置为1×10-7,X轴信噪比由-73 dB以1 dB的步长增长至-56 dB,可以得到Y轴对应的雷达目标检测概率Pd。可以发现当干扰功率逐渐加大时(SIR的值由0 dB变化到-30 dB),雷达的检测概率Pd逐渐恶化。例如,当SIR=-20 dB时,雷达的检测概率即使在信噪比最大的-56 dB也不能达到1;当SIR=-30 dB时,雷达的检测概率全部为0,说明干扰信号已经完全压制了AN/TPY-2的雷达回波。

图11 存在干扰时的雷达检测概率与信噪比的关系Fig.11 Radar detection probability versus SNR facing interference

4 结束语

分析了AN/TPY-2雷达的参数,并基于雷达方程研究了该雷达的性能。经过数值计算发现前置模式时，雷达的最大作用距离较远,对我国的战略威慑力构成较大影响。基于SystemVue软件搭建了验证雷达方程的仿真平台,平台可以对雷达方程涉及到的所有参数进行验证。通过将干扰机的信号注入雷达接收机,使得一定距离时的雷达检测概率明显降低,可以明显降低AN/TPY-2雷达的检测性能。但是,考虑到雷达信号处理技术的发展以及氮化镓高功率效率器件的发展,升级版的AN/TPY-2雷达作用距离也会进一步提高。未来,可以使用更先进的干扰措施对抗AN/TPY-2雷达,平时通过先进的信号情报获取该雷达的信号参数建立信号数据库,再通过数字射频存储、认知电子战等形式的电子对抗措施降低AN/TPY-2雷达的作用距离。

[1] 陈士涛,杨建军,马丽.末端高空区域防御系统及其作战部署[J].飞航导弹,2011(5):61-65.

CHEN S T, YANG J J, MA L. The terminal high altitude area defense system and its operational deployment[J]. Aerodynamic Missile, 2011(5):61-65.

[2] Raytheon Company. AN/TPY2:Army Navy/transportable radar surveillance-model 2[EB/OL].[2017-03-06].https:∥www.raytheon.com/capabilities/products/antpy21,2009.

[3] NORTON K A, OMBERG A C. The maximum range of a radar set[J]. Proceedings of the Institute of Engineers, 1947, 35(1): 4-24.

[4] BARTON D K. Radar system analysis and modeling[J]. IEEE Aerospace & Electronic Systems Magazine, 2005, 20(4):23-25.

[5] MERRILL I S. Radar handbook[J]. Beijing: Publishing House of Electronics Industry, 2003.

[6] BARTON D K. Radar equations for modern radar[M]. Beijing: Publishing House of Electronics Industry, 2016.

[7] GEORGE L,THEODORE P. Ballistic missile defense: radar range calculations for the AN/TPY2 X band and NAS proposed GBXRadars[EB/OL].[2012-09-21].https:∥mostlymissiledefense.com/2012/09/21/ballistic-missile-defense-radar-range-calculations-for-the-antpy-2-x-band-and-nas-proposed-gbx-radas-septem-ber-21-2012/#more-420.

[8] SKOLNIK M I. Introduction to radar systems[M]. 3rd ed. New York: McGraw-Hill, 2001.

[9] SARCIONE M, MULCAHEY J, SCHMIDT D, et al. The design, development and testing of the terminal high altitude area defense solid state phased array (formerly ground based radar)[C]∥Proc.of the IEEE International Symposium on Phased Array Systems and Technology, 1996: 260-265.

[10] BROOKNER E. GaN transistors for radar[J]. Microwave Journal, 2008(1):5-11.

[11] BROOKNER E. Phased-array and radar astounding breakthroughs—an update[C]∥Proc.of the IEEE Radar Conference, 2008: 1-6.

[12] KOPP B A. S-and X-band radar transmit/receive module overview[C]∥Proc.of the IEEE Radar Conference, 2007:948-953.

[13] ALABASTER C. Pulse Doppler radar: principles, technology, applications[M]. Edison, NJ: Scitech Publishing, 2012.

[14] 丁鹭飞. 雷达原理[M]. 北京:电子工业出版社, 2014.

DING L F. Radar pinciple[M]. Beijing: Publishing House of Electronics Industry, 2014.

[15] 张光义. 多波束形成技术在相控阵雷达中的应用[J]. 现代雷达, 2007, 29(8):1-6.

ZHANG G Y. Application of multi-beam formation technologies in phased array radar[J].Modern Radar, 2007, 29(8):1-6.

[16] 张光义,赵玉洁.相控阵雷达技术[M].北京:电子工业出版社,2007.

ZHANG G Y, ZHAO Y J. Phased array radar technology[M]. Beijing: Publishing House of Electronics Industry, 2007.

[17] 毕增军, 鲁力, 徐晨曦,等. 相控阵雷达资源管理技术的发展与应用研究[J]. 现代防御技术, 2015, 43(5) :116-123.

BI Z J, LU L, XU C X, et al. Development and application of phased array radar resource management[J]. Modern Defense Technology, 2015, 43(5):116-123.

[18] 王娜,谭顺成,王国宏,等.基于IMM的高脉冲重复频率雷达解距离模糊方法[J].系统工程与电子技术,2011,33(9):1970-1977.

WANG N, TAN S C, WANG G H, et al. Range ambiguity resolving of HPRF radar based on IMM[J]. Systems Engineering and Electronics, 2011, 33(9):1970-1977.

[19] 翟颖颖. 高脉冲重复频率雷达解距离模糊方法的研究[D]. 哈尔滨： 哈尔滨工业大学, 2005.

ZHAI Y Y. Study on the range ambiguity resolving method of high pulse repetition frequency radar[D]. Harbin: Harbin Institute of Technology, 2005.

[20] 周闰, 高梅国, 戴擎宇,等. 余差查表法解单目标距离模糊的分析和仿真[J]. 系统工程与电子技术, 2002, 24(5):30-31.

ZHOU R, GAO M G, DAI Q Y, et al. Analysis and simulation for ambiguity resolving using residues’ difference look-up table[J]. Systems Engineering and Electronics,2002,24(5):30-31.