结合非正交子载波的空频索引调制技术
王 媛, 刘文龙, 金明录
(大连理工大学信息与通信工程学院, 辽宁 大连 116024)
0 引 言
根据升级的长期演进(long term evolution-advanced,LTE-A)标准,当下第四代(the 4th generation,4G)移动通信技术能够支低速移动特性下1 Gbps和高速移动特性下100 Mbps的下行峰值数据传输速率,其强大的优势给人们的生活带来了巨大的变革。然而,随着社会的迅速发展,人们对于移动通信技术的要求与日俱增。作为下一代移动通信技术,第五代(the 5th generation,5G)移动通信技术将面向2020年以后的移动通信需求,即支持在4G的基础上提高至少10倍的峰值数据传输速率、频谱效率和能量效率,以及1 000倍的系统容量和25倍的平均小区吞吐量,从而实现零时延、高可靠、低能耗的移动通信系统。为了实现5G的要求,国内外学者们不断进行着物理层的探索和创新,大规模多输入多输出(multiple input multiple output,MIMO)技术、基于滤波器的正交频分复用(orthogonal frequency division multiplexing,OFDM)技术、稀疏码多址接入技术以及毫米波通信技术等将有可能成为5G的关键技术[1]。
索引调制(index modulation,IM)技术自提出以来引起学者的广泛关注,由于其通过索引携带部分信息从而实现相比传统系统更高的频谱和能量效率,故期待其能够在5G中获得应用。目前索引调制技术包括两部分,即空间调制(spatial modulation,SM)技术和OFDM-IM技术[2]。作为一种特殊的MIMO技术,SM不仅通过发送符号传递信息,同时利用激活的发送天线序号携带信息,由于每次只有一根天线被激活,所以在发送端只需要一个射频链路,相比MIMO系统,其大大降低了系统成本;另外由于其可以避免天线间的干扰,使接收端设计较为简单,从而提升了系统的整体性能[3-4]。索引调制OFDM技术的思想来源于SM,即其不仅通过发送符号传递信息,同时利用激活的子载波序号携带信息,相比传统的OFDM,其能够有效降低峰均比(peak to average power ratio,PAPR)和载波间干扰(inter-carrier interference,ICI),并且实现了低阶调制下更好的系统性能[5-8]。近几年来,对于索引调制的研究不断发展,空移键控调制(space shift keying,SSK)[9]、广义OFDM-IM[10]、MIMO-OFDM-IM[11]等技术已被提出。
最近,将这两种索引调制技术进行结合广义空频索引调制技术(generalized space and frequency index modulation,GSFIM)被提出,该技术通过三部分发送信息,即星座符号、激活的发送天线序号和激活的子载波序号。仿真结果显示相比已在4G中应用的MIMO-OFDM,其能够实现中高信噪比下更好的误码率性能[12]。进而,文献[13]将空频索引调制技术应用于车辆与基础设施(vehicle-to-infrastructure,V2I)的通信系统中来减小由多普勒效应产生的ICI,并通过仿真结果证明了相比传统SM-OFDM其能够实现更好的误码率性能。然而GSFIM的信息分配方式导致了接收端高复杂度的检测。在此,讨论一种特殊形式的空频索引调制技术,即FQAM/FPSK-SM,其将FQAM/FPSK(frequency and quadrature amplitude modulation/frequency and phase shift keying)调制技术[14]与SM相结合,大大简化了系统结构。
近几年,由于非正交MFSK可以提高频带效率而引起学者研究。文献[15]提出了非正交MFSK的对数似然比检测算法,并给出了理论推导。进而,一种非均匀频带间隔的非正交MFSK系统被提出,作者通过理论分析以及仿真结果证明了其所带来的频谱效率的提升[16]。文献[17-18]将非正交子载波思想发展到OFDM系统中,由此展望了5G的前景。在本论文中,将此非正交子载波思想引入FQAM/FPSK-SM系统中,提出非正交FQAM/FPSK-SM,有效地提高了频谱效率。由于其每次只激活一个子载波,从而避免了通常意义上的非正交干扰,这也是非正交子载波思想应用于FQAM/FPSK-SM系统中的优势。仿真结果表明在不同的参数配置下,通过调整压缩系数,非正交FQAM/FPSK-SM系统不仅能够带来频谱效率的提升,而且能够在发送速率相同的前提下达到与正交系统基本相同的误码率(bit error rate,BER)性能,提高了系统的单位带宽吞吐量。
1 FQAM/FPSK-SM系统模型
本节首先介绍FQAM/FPSK调制技术,给出以FQAM为例的调制示意图。然后介绍FQAM/FPSK-SM的系统模型,并给出该系统的三维映射示意图以及具体映射表。该系统采用的信道模型为频率选择性衰落和加性高斯白噪声信道。
1.1 FQAM/FPSK调制技术
FQAM/FPSK调制示意图如图1所示(在此以4QAM为例),M阶FQAM/FPSK调制是由Mf阶FSK调制和Mq阶QAM/PSK调制结合而成,发送比特数为n=log2(M),其中M=MfMq,即nf=log2(Mf)比特信息用来选择激活频率,nq=log2(Mq)比特信息用于进行QAM/PSK的星座调制。Mf个子载波间相互正交,满足关系式
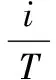
(1)
式中,T为FQAM/FPSK符号周期。由于每个QAM/PSK符号可以表示为sm=Amejθm(PSK调制中Am=1),则假设发送端第m个调制符号经第i个频率在[0,T)时间内发送时,发送信号表达式为
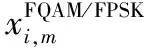
(2)
式中,1≤i≤Mf,1≤m≤Mq,当t∈[0,T)时pT(t)=1,其余情况下pT(t)=0[14]。
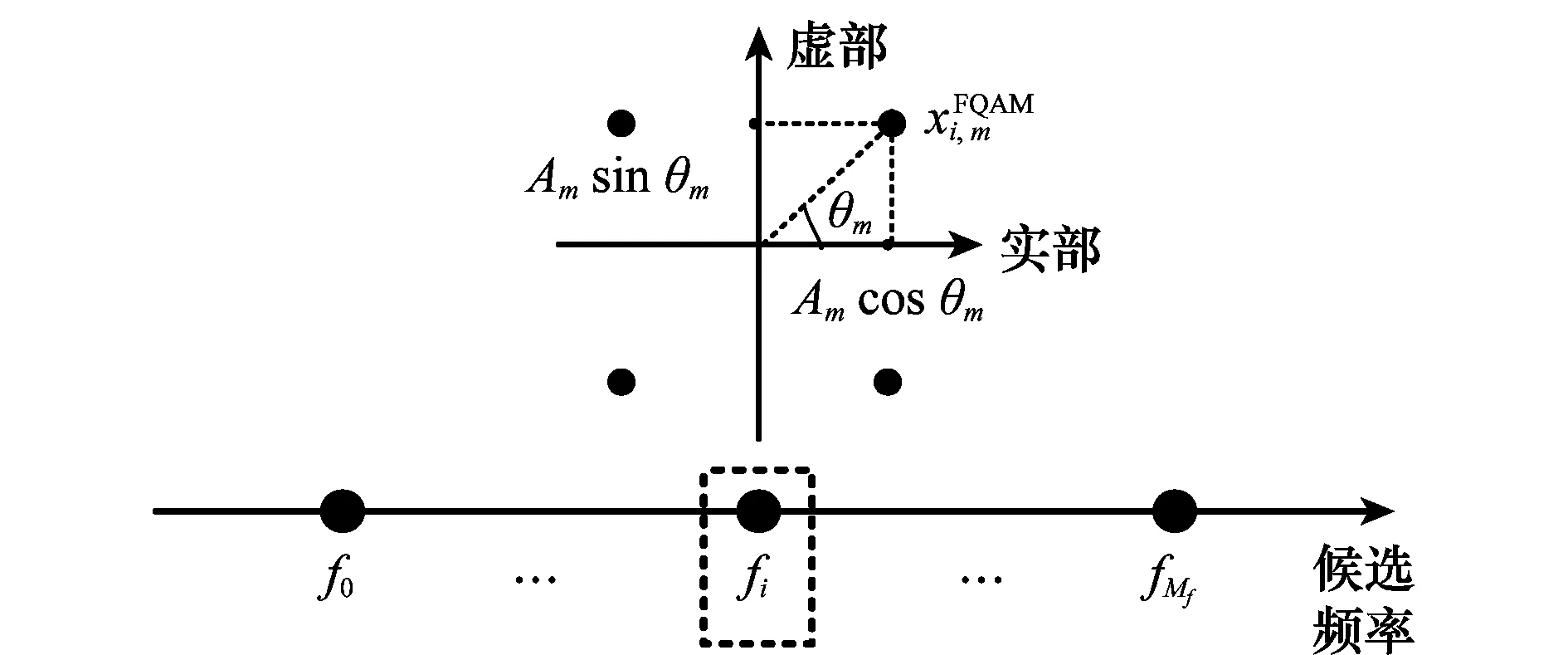
图1 FQAM/FPSK调制示意图Fig.1 FQAM/FPSK modulation diagram
1.2 FQAM/FPSK-SM系统模型
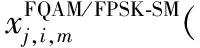
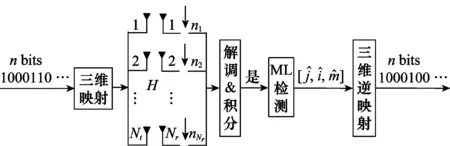
图2 FQAM/FPSK-SM系统模型Fig.2 FQAM/FPSK-SM system model
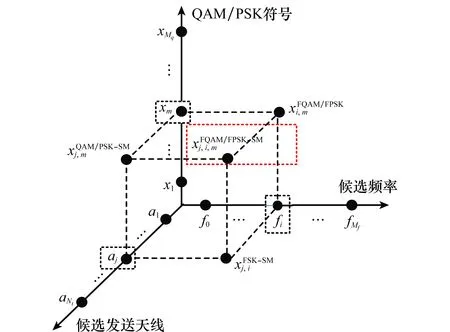
图3 FQAM/FPSK-SM三维映射示意图Fig.3 Three-dimensional mapping diagram of FQAM/FPSK-SM
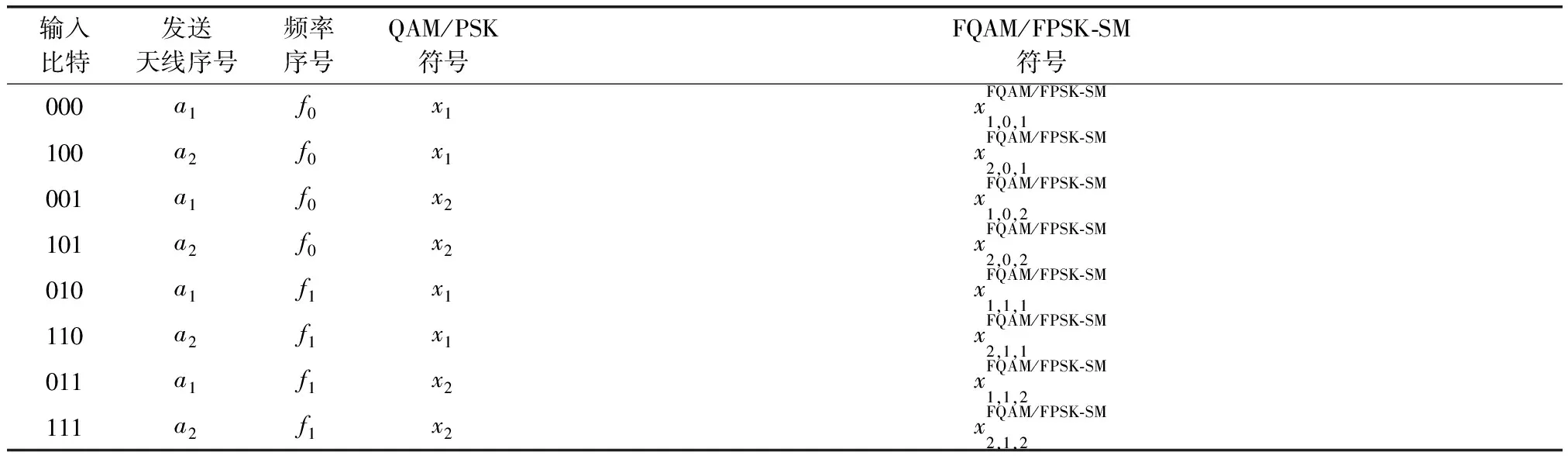
输入比特发送天线序号频率序号QAM/PSK符号FQAM/FPSK⁃SM符号000a1f0x1xFQAM/FPSK⁃SM1,0,1100a2f0x1xFQAM/FPSK⁃SM2,0,1001a1f0x2xFQAM/FPSK⁃SM1,0,2101a2f0x2xFQAM/FPSK⁃SM2,0,2010a1f1x1xFQAM/FPSK⁃SM1,1,1110a2f1x1xFQAM/FPSK⁃SM2,1,1011a1f1x2xFQAM/FPSK⁃SM1,1,2111a2f1x2xFQAM/FPSK⁃SM2,1,2
由于在FQAM/FPSK-SM系统中只有一个频率被激活用于携带星座调制信息,所以当第i个频率被激活时,单根天线的发送符号向量表示为
(3)
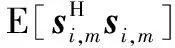
H=[H1H2…HNt]
(4)
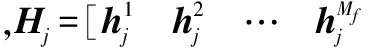
N=[n1n2…nMf]
(5)
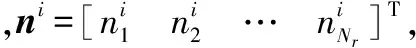
(6)
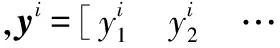
FQAM/FPSK-SM系统的接收端采用最大似然(maximum likelihood,ML)检测技术,由于SM系统在检测时是根据空间信道的差异性来判断激活天线的索引序号,且在通常的研究中均假设接收端已知完整的信道信息[4-6],所以本文同样假设接收端已知完整的信道信息。进而,根据ML检测原则可得
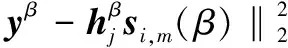
(7)
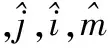
2 非正交FQAM/FPSK-SM频带设计与系统分析
为了提升频谱效率,本节在FQAM/FPSK-SM系统模型的基础上,提出非正交FQAM/FPSK-SM。首先介绍非正交子载波的频带设计并给出解调分析,其次对所提系统的频谱效率以及星座图特点进行了分析。
2.1 非正交子载波的频带设计
在上述FQAM/FPSK-SM系统中,Mf个子载波之间相互正交,满足关系式(1)。图4给出了非正交频带设计示意图,在此以两个子频带为例,中心频率分别为f1和f2。可以看到,图4(a)中的两个子频带的频率间隔为1/T,此时子载波之间相互正交。图4(b)、图4(c)和图4(d)均在图4(a)的基础上将两个子频带的频率间隔做不同程度的压缩,满足关系式
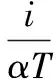
(8)
式中,将α定义为压缩系数,可以看出,随着α的增加,两个子频带的中心频率越来越靠近,即频率间隔逐渐缩小,节省的频带资源越来越多。图4中蓝虚线将正交时的频率间隔1/T二等分,红虚线将其三等分,故图4(b)中α=1.5,两个子频带相比正交时可以节省1/3T的带宽,n个子频带可以节省(n-1)/3T的带宽;图4(c)中α=2,两个子频带可以节省1/2T的带宽,n个子频带可以节省(n-1)/2T的带宽;图4(d)中α=3,两个子频带可以节省2/3T的频带,n个子频带可以节省2(n-1)/3T的带宽。
在通常的多载波通信系统中,虽然非正交频带可以节省频带资源,但会带来子载波间的非正交干扰。而在FQAM/FPSK-SM系统中,由于每个时刻只激活一个子载波,所以不存在通常意义上的非正交干扰,这也是本文将非正交频带思想引入该系统的出发点之一。
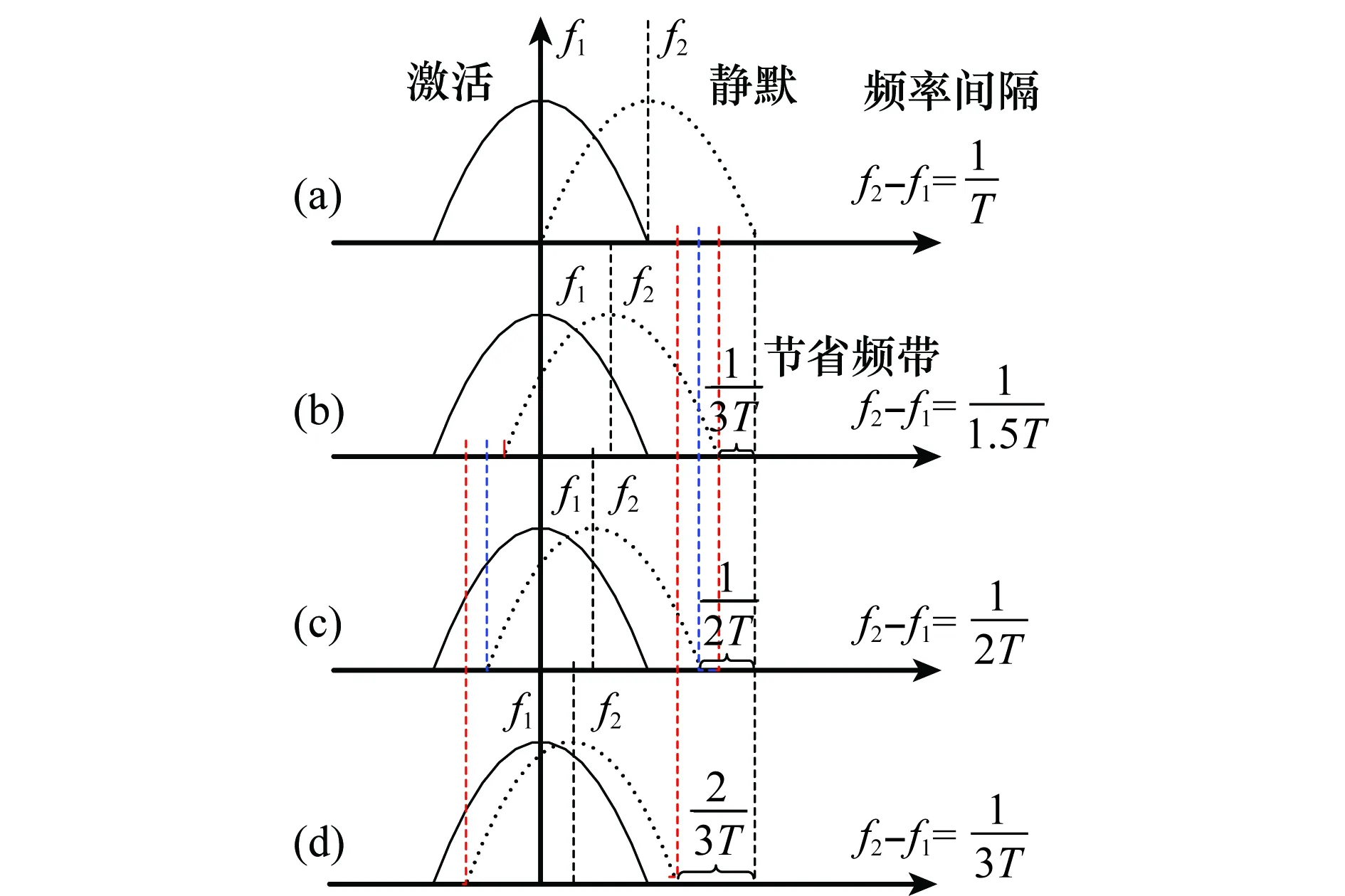
图4 非正交子载波的频带设计示意图Fig.4 Frequency spectrum diagram of non orthogonal subcarrier
然而,在非正交FQAM/FPSK-SM系统的接收端仍然存在解调干扰。在此,假设发送端f1被激活同时携带信息,f2处于静默状态,如图4所示。接收端对接收的每个子信道的信号进行解调,首先解调第一路信号,经过T时间内积分可得(为方便理解和表示,在此我们考虑单天线收发情况)
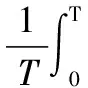
(9)
式中,y(t)为接收信号;h1和n1分别为第一个子信道的复衰落系数和高斯白噪声,分别服从均值为0、方差为1和均值为0、方差为σ2/Mf的复高斯分布。由于发送端只有一个子载波被激活并携带信息,所以对于这一路信号,无论是正交频带还是非正交频带,解调后得到的均是包含信道衰落以及噪声的发送符号,如式(9)所示。接下来对第二路信号进行解调,经过T时间内积分可得
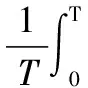
(10)
式中,n2为第二个子信道的高斯白噪声,服从的分布同第一个子信道。当子载波间相互正交时,f1上的接受信号不会对f2上的接收信号产生影响,即解调第二路信号后得到的只有噪声,所以接收端可以对激活频率直接作出判决。而子载波间非正交时,解调第二路信号后得到的结果不只有噪声,还会存在解调干扰,如式(10)中的第一项。将此解调干扰记为I,随着α的增加,I的能量越来越大,其会对激活频率的检测产生影响,进而影响其他部分的检测,从而降低系统的BER性能。
然而,在所提出的非正交FQAM/FPSK-SM系统中,在不同的参数配置下,通过调整α,不仅可以带来频谱效率的提升,而且能够在相同发送速率的条件下达到与正交系统基本一致的性能,该结论在第3节仿真中得以证明。
2.2 非正交系统分析
为了进一步理解非正交FQAM/FPSK-SM系统的优势和特点,本节对该系统的频谱效率和星座图进行了分析。
2.2.1 频谱效率
当采用正交Mf-FSK调制时,假设系统的总带宽为B,符号速率为Rs,即可表示为
B=NRs
(11)
此时B被N个正交子频带复用,频谱效率可表示为
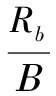
(12)
式中,Rb为比特速率,此时Mf为整数,且Mf=N。当N=3时,式(12)取得最大值nb=0.528 3 bit/s/Hz,对于正交Mf-FSK而言,该值是最大的频谱效率。
在FQAM/FPSK-SM中,式(12)变为
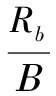
(13)
当采用非正交子载波的频带设计时,随着α的增加,Mf不一定为整数,且Mf>N,所以相比FQAM/FPSK-SM,非正交FQAM/FPSK-SM可以提高频谱效率。表2给出了Nt=2,Mq=2时不同N的条件下改变α的频谱效率,从表中可以看出随着α的增加,nb越来越大。

表2 非正交FQAM/FPSK-SM频谱效率
2.2.2 星座分析
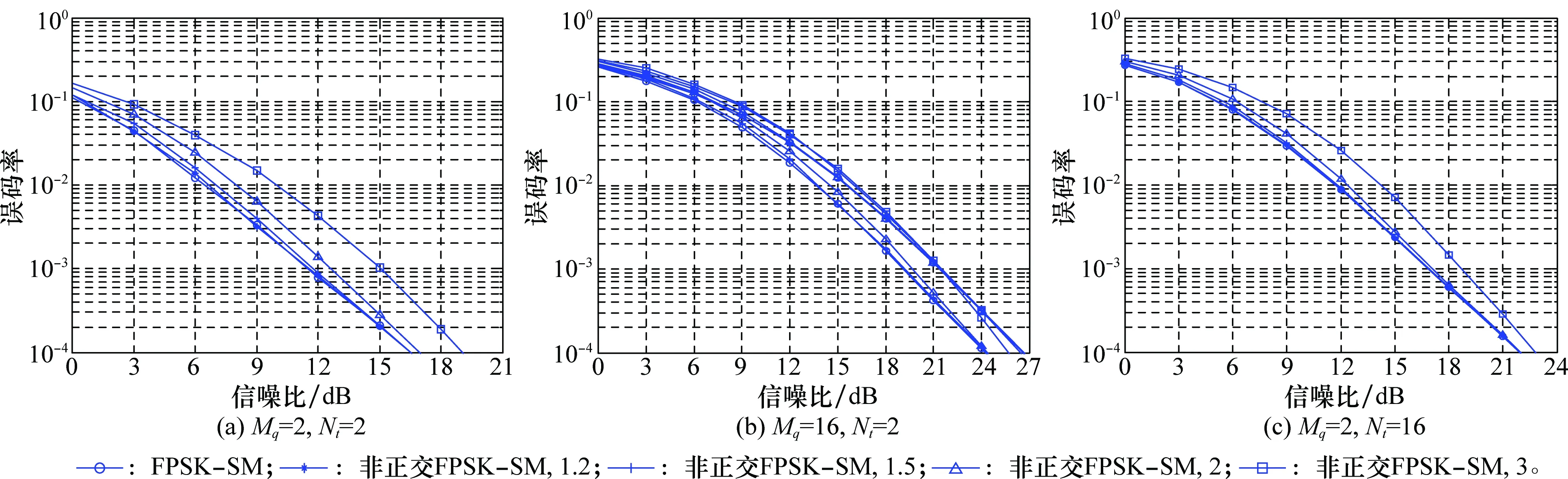
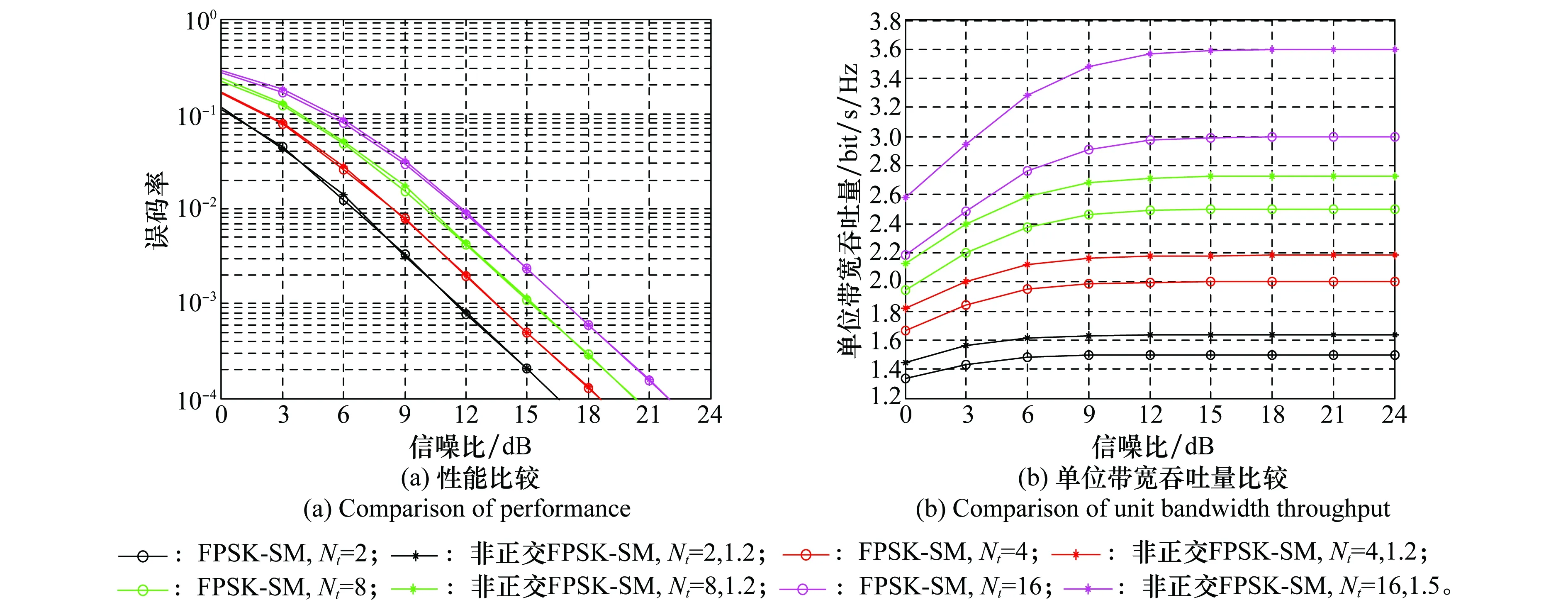
16-QAM/PSK调制的星座图如图5中实心点所示,可以看到,它们的最小欧氏距离lm均为两个相邻星座点之间的距离。而对于FQAM/FPSK调制,只有被激活的子载波会携带信息,未被激活的子载波不携带信息,故其星座图在原有的基础上增加了一个星座点,即原点,如图5中空心点所示。此时FPSK调制星座图的最小欧氏距离li仍为两个相邻星座点之间的距离,即li=lm;而FQAM调制星座图的最小欧氏距离li变为原点与离其最近的星座点之间的距离,注意到此时li 图5 FQAM/FPSK调制星座图最小欧氏距离示意图Fig.5 Minimum Euclidean distance diagram of FQAM/FPSK modulation constellation 为了体现α对非正交系统性能的影响,首先给出了非正交FQAM/FPSK-SM系统下Mq=2、Nt=2以及α分别为1.2、1.5、2、3时的BER性能仿真曲线,如图6(a)所示。可以看出,当α=1.2时,非正交系统与正交系统的BER曲线重合,而随着α的增加,I对检测的影响越来越大,故非正交系统与正交系统的BER曲线逐渐偏离,性能差距逐渐增加。在图6(b)和图6(c)中,分别给出Mq=16、Nt=2情况下α=1.5、2、3和Mq=2、Nt=16情况下α=1.2、1.5、2、3时的BER性能仿真曲线。可以看到,在图6(b)中α=2的条件下非正交FPSK-SM的BER曲线仍然能够与正交系统保持重合,而非正交FQAM-SM仅在α=1.5时与正交系统重合,由此验证了第2.2.2节中的分析。另外,随着信噪比的增加,α更高的非正交曲线也逐渐接近正交曲线,在α=3时,非正交FPSK-SM从18dB开始与FPSK-SM的曲线重合。在图6(c)中α=1.5的条件下非正交FPSK-SM系统的BER曲线能够与正交系统保持重合,同样,随着信噪比的增加,α=2、3的曲线也逐渐接近正交曲线。由此说明随着Mq或者Nt的增加,I对该系统的检测产生的影响逐渐减小,且在α较大时,中高信噪比下非正交系统具有更大的优势。以上仿真中Mf=Nr=2。 图6 不同α条件下非正交FQAM/FPSK-SM与FQAM/FPSK-SM系统的性能比较Fig.6 Performance comparison of non orthogonal FPSK-SM with FPSK-SM under different α 为了进一步证明上述结论,分别给出不同Mq和不同Nt时非正交FQAM/FPSK-SM与FQAM/FPSK-SM的性能比较和单位带宽吞吐量的比较。单位带宽吞吐量的表达式表示为 (14) 式中,Pb为系统的BER。 图7和图8分别为不同Mq和Nt条件下,非正交FQAM/FPSK-SM与FQAM/FPSK-SM的性能比较和单位带宽吞吐量比较。 图7 不同Mq条件下非正交FQAM/FPSK-SM与FQAM/FPSK-SM的性能比较和单位带宽吞吐量比较Fig.7 Performance and unit bandwidth throughput comparison of non orthogonal FQAM/FPSK-SM with FQAM/FPSK-SM under different Mq 图7(a)中给出Mf=2时不同Mq条件下非正交系统与正交系统的BER性能仿真结果。在非正交FPSK-SM中当Mq分别为2、4、8、16时,根据图6的仿真结果,本文分别选择α=1.2,1.2,1.5,2进行了仿真,而在非正交FQAM-SM中,在Mq=16时选择了α=1.5的情况。可以看出,在不同的参数配置下,通过调整α,非正交FQAM/FPSK-SM系统能够在发送比特速率相同的前提下达到与正交系统相同的BER性能。且随着Mq的增加,α逐渐增大,故节省的频带资源越来越多。为了进一步证明其优势,在图7(a)的仿真结果基础之上,图7(b)中给出相同参数配置下的单位带宽吞吐量的仿真结果。可以看出,相比正交系统,非正交FQAM/FPSK-SM系统可以提升单位带宽的吞吐量,且随着Mq的增加,增益越来越大。在非正交FPSK-SM系统中,Mq=16时极值处提升了1 bit/s/Hz,而低信噪比处的增益相对较小。图7的仿真中Nt=Nr=2。 图8 不同Nt条件下非正交FQAM/FPSK-SM与FQAM/FPSK-SM的性能比较和单位带宽吞吐量比较Fig.8 Performance and unit bandwidth throughput comparison of non orthogonal FQAM/FPSK-SM withFQAM/FPSK-SM under different Nt 图8(a)中给出Mf=2时不同Nt条件下非正交系统与正交系统的BER性能仿真结果。在非正交FPSK-SM中,当Nt分别为2、4、8、16时,分别选择α=1.2,1.2,1.2,1.5进行了仿真,进而在图8(a)的仿真结果基础之上,图8(b)中给出相同参数配置下的单位带宽吞吐量的仿真结果。注意到,图8可以得到与图7基本一致的结论,但是相比图7,随着Nt的增加,单位带宽吞吐量增益的提升相对较小,Nt=16时极值处提升了0.6 bit/s/Hz。图8的仿真中Mq=Nr=2。 图9中分别给出Mf=4,8时,Mq=16、Nt=2和Mq=2、Nt=16的条件下非正交FQAM/FPSK-SM与FQAM/FPSK-SM的BER性能仿真结果以及单位带宽吞吐量的仿真结果。 图9 Mf=4, 8条件下非正交FQAM/FPSK-SM与FQAM/FPSK-SM的性能比较和单位带宽吞吐量比较Fig.9 Performance and Unit bandwidth throughput comparison of non orthogonal FQAM/FPSK-SM with FQAM/FPSK-SM under Mf=4, 8 可以看到,图9(a)中非正交系统的性能曲线与正交系统基本重合,图9(b)中非正交系统同样能够带来单位带宽吞吐量的增益。Mf=4时,在非正交FPSK-SM中,Mq=16、Nt=2时,极值处提升了1 bit/s/Hz,Mq=2、Nt=16时,极值处提升了0.6 bit/s/Hz;在非正交FQAM-SM中,Mq=16、Nt=2时,极值处提升了0.6 bit/s/Hz。Mf=8时,3种情况下分别提升了0.8 bit/s/Hz、0.4 bit/s/Hz、0.4 bit/s/Hz。图9的仿真中,Nr=2。 首先介绍了一种特殊形式的空频索引调制技术,即FQAM/FPSK-SM,为了方便理解,给出了该系统的三维映射示意图以及具体的映射表。相比GSFIM,FQAM/FPSK-SM具有较为简单的信息分配方式和较低复杂度的检测。为了进一步提升该系统的频谱效率,本文将非正交子载波思想引入其中,提出非正交FQAM/FPSK-SM,给出了非正交子载波的频带设计和解调分析,并对频谱效率的提升以及星座图特点做了分析。仿真结果表明,在不同的参数配置下,通过调整α,非正交FQAM/FPSK-SM系统不仅可以提升频谱效率,而且能够在发送速率相同的前提下达到与正交系统基本相同的性能,提高了系统的单位带宽吞吐量。然而本文没有给出不同参数配置下的最优α,故没有得出最大的单位带宽吞吐量增益,这将是下一步的研究内容。 [1] WANG C X, HAIDER F, GAO X, et al. Cellular architecture and key technologies for 5G wireless communication networks[J]. IEEE Communications Magazine, 2014, 52(2): 122-130. [2] BASAR E. Index modulation techniques for 5G wireless networks[J].IEEE Communications Magazine,2016,54(7):168-175. [3] MIETZNER J, SCHOBER R, LAMPE L, et al. Multiple-antenna techniques for wireless communications-a comprehensive literature survey[J]. IEEE Communications Surveys and Tutorials, 2009, 11(2): 87-105. [4] MESLEH R Y, HAAS H, SINANOVIC S, et al. Spatial modulation[J]. IEEE Trans.on Vehicular Technology, 2008, 57(4): 2228-2241. [5] JEGANATHAN J, GHRAYEB A, SZCZECINSKI L. Spatial modulation: optimal detection and performance analysis[J]. IEEE Communications Letters, 2008, 12(8): 545-547. [6] RENZO M D, HAAS H. Bit error probability of SM-MIMO over generalized fading channels[J]. IEEE Trans.on Vehicular Technology, 2012, 61(3): 1124-1144. [7] BASAR E, AYGOLU U, PANAYIRCI E, et al. Orthogonal frequency division multiplexing with index modulation[J]. IEEE Trans.on Signal Processing, 2013, 61(22): 5536-5549. [8] XIAO L X, XU B, BAI H R, et al. Performance evaluation in PAPR and ICI for ISIM-OFDM systems[C]∥Proc.of the International Workshop on High Mobility Wireless Communications, 2014: 84-88. [9] JEGANATHAN J, GHRAYEB A, SZCZECINSKI L, et al. Space shift keying modulation for MIMO channels[J]. IEEE Trans.on Wireless Communications, 2009, 8(7): 3692-3703. [10] FAN R, YU Y J, GUAN Y L. Generalization of orthogonal frequency division multiplexing with index modulation[J]. IEEE Trans.on Wireless Communications, 2015, 14(10): 5350-5359. [11] WANG S, XU B, BAI H R, et al. MIMO-OFDM with interleaved subcarrier-index modulation[C]∥Proc.of the 10th International Conference on Wireless Communications, Networking and Mobile Computing, 2014: 35-37. [12] DATTA T, ESHWARAIAH H S, CHOCKALINGAM A. Generalized space-and-frequency index modulation[J]. IEEE Trans.on Vehicular Technology, 2016, 65(7): 4911-4924. [13] LIU Y, ZHANG M, WANG H, et al. Spatial modulation orthogonal frequency division multiplexing with subcarrier index modulation for V2X communications[C]∥Proc.of the International Conference on Computing, Networking and Communications, 2016: 1-5. [14] HONG S, SAGONG M, LIM C, et al. FQAM: a modulation scheme for beyond 4G cellular wireless communication systems[C]∥Proc.of the IEEE Globecom Workshops, 2013: 25-30. [15] NOJIMA D, NAGAO Y, KUROSAKI M, et al. Derivation of log-likelihood ratio for M-ary non-Orthogonal FSK wireless system[C]∥Proc.of the IEEE Vehicular Technology Conference, 2012: 1-5. [16] DAS A, RAO B D. Adaptive non orthogonal MFSK[J]. IEEE Trans.on Signal Processing, 2014, 62(23): 6077-6088. [17] ZHANG P J, FANG L, JIANG W, et al. A novel orthogonal transmission scheme for non-orthogonal multi-carrier signal[C]∥Proc.of the 3rd IEEE International Conference on Broadband Network and Multimedia Technology, 2010: 467-471. [18] DOMMEL J, BOCCOLINI G, RASCHKOWSKI L, et al. 5G in space: PHY-layer design for satellite communications using non-orthogonal multi-carrier transmission[C]∥Proc.of the 7th Advanced Satellite Multimedia Systems Conference and the 13th Signal Processing for Space Communications Workshop, 2014: 190-196.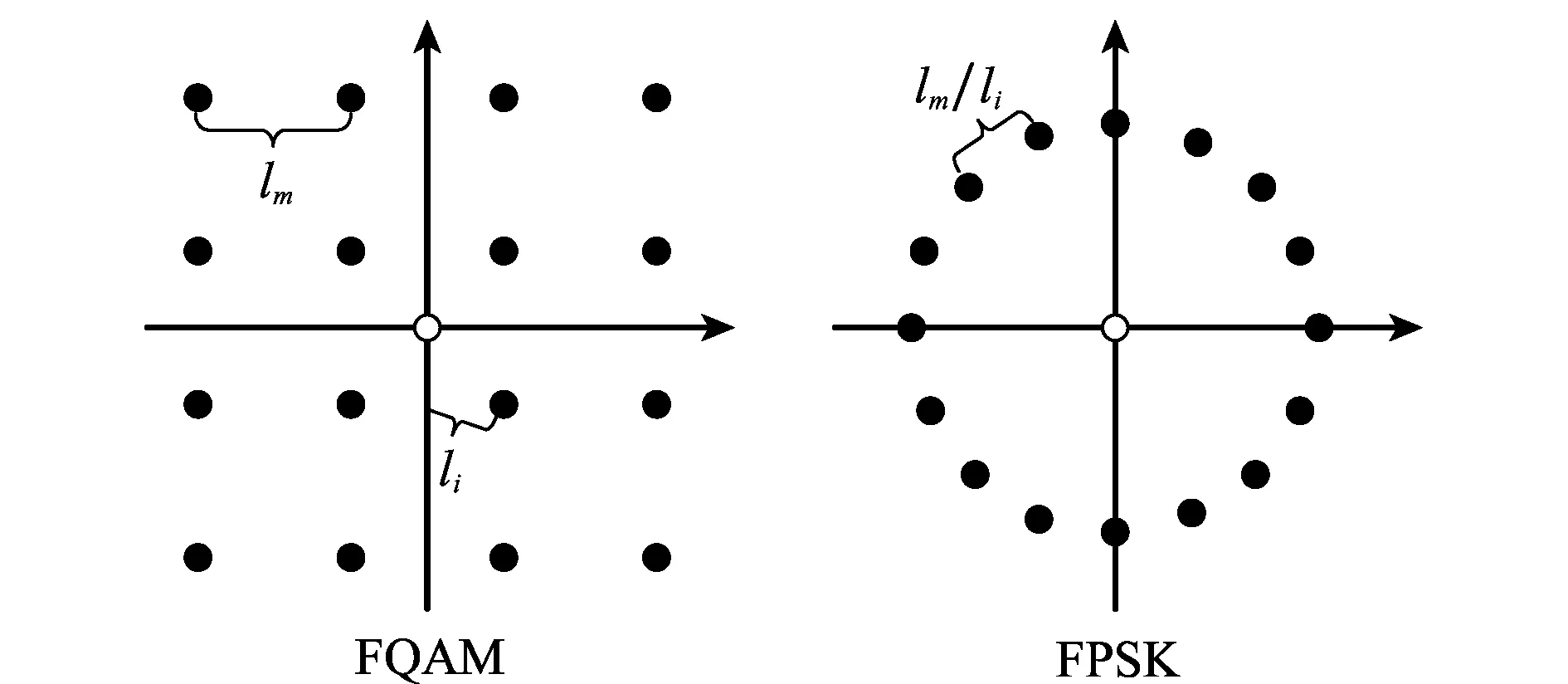
3 仿真结果
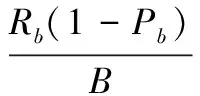
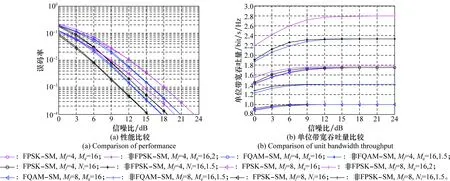
4 结 论

