机动目标距离徙动校正与检测算法

贺雄鹏, 廖桂生, 许京伟, 黄鹏辉, 魏嘉琪

(西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071)

0 引 言

随着高性能武器装备的发展,以新一代战斗机(具有超声速和高机动等特点)为代表的运动目标,对传统雷达的探测能力提出了严峻的挑战,高机动目标检测与高精度运动参数估计研究受到广泛的关注[1-3]。目标检测与参数估计对于雷达目标成像、目标跟踪与识别等具有重要意义[4-6]。脉冲相参积累可以有效提高目标输出信噪比,因此通过补偿不同脉冲之间的相位起伏,可以提高雷达的检测性能与目标参数估计性能[7-8]。然而,由于目标的机动性,在积累时间内会产生距离徙动和多普勒徙动现象,严重降低相参积累性能。

在积累时间内,目标的径向速度会引起距离走动和多普勒频偏,目标的径向加速度会导致距离弯曲和多普勒扩散。一阶Keystone变换在每一个频点上,通过对慢时间轴尺度变换来实现距离走动校正[9-10]。文献[11]提出的Radon傅里叶变换(Radon-Fourier transform, RFT)方法对目标运动参数搜索估计,可有效地在积累时间内对目标能量进行相干积累,但是运算复杂度高。一阶Keystone变换和RFT方法均没有考虑目标加速度产生的距离弯曲和多普勒扩散问题,在距离弯曲和多普勒扩散不能忽略的情况下,会造成积累性能的损失。

文献[12]利用二阶Keystone变换解决距离弯曲,然后通过估计线性走动的斜率得到多普勒中心频率参数,最后利用Wigner-Ville分布(Wigner-Ville distribution, WVD)方法[13]估计出多普勒调频率,完成二次相位补偿和方位压缩。然而,多普勒中心频率与调频率需要参数搜索估计,计算复杂度高。文献[14-15]提出了邻近互相关算法进行距离徙动的校正与多普勒徙动的降阶,但是需要满足目标在相邻脉冲内的徙动量不超过一个距离单元。文献[16]提出的RLVD (Radon-Lv’s distribution)算法通过参数搜索有效完成运动目标参数估计,但是计算复杂度高。文献[17]提出了Radon-分数阶傅里叶变换(Radon-fractional Fourier transform, RFRFT)算法,通过对距离、速度和加速度的搜索完成机动目标参数估计,计算复杂度高。为了减少运算量,文献[1]提出了改进的两维频域匹配滤波算法,通过搜索目标加速度,在两维频域构造匹配函数进行解耦合,然而这类方法在小时宽带宽积条件下并不适用。

针对于多普勒频率徙动问题,典型的方法有最大似然估计方法[18]、非线性瞬时最小均方误差算法[19]、积分立方相位函数算法[20]、高阶模糊函数算法[21]、短时傅里叶变换[22]、WVD方法[23]。然而,这些方法无法避免计算复杂度高,交叉项干扰等问题,并且这些方法均没有考虑距离徙动。文献[24]构造近似匹配函数补偿距离徙动存在误差,然后利用时间反转变换进行多普勒徙动校正。

综合上述方法的优点与不足,提出了一种基于频率轴反转和广义尺度傅里叶变换(generlized scaled Fourier transform, GSCFT)的距离徙动校正与参数估计算法。首先在距离频域-方位时域通过频率轴反转变换进行距离徙动校正,然后逆傅里叶变换(inverse Fourier transform, IFT)到距离时域-方位时域;利用WVD变换核与GSCFT估计出目标的多普勒中心频率与多普勒调频率;利用估计出的参数构造相位补偿函数来解决多普勒徙动;最后在距离-多普勒域完成目标能量聚焦。

1 回波信号模型

假设雷达发射线性调频(linear frequency modulation, LFM) 信号

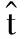
(1)

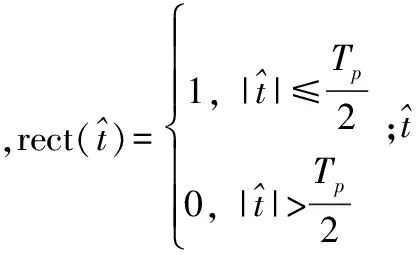
(2)

式中,r0表示目标距离雷达的初始斜距;φ1和φ2分别表示为目标的径向速度和加速度;tm(tm=m·PRT)表示慢时间,PRT为脉冲重复周期(pulse recurrence time, PRT),m=0,1,2,…,M-1;M表示相干积累脉冲数。

忽略噪声,雷达接收基带回波信号可以表示为

(3)

(4)

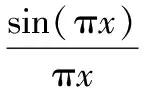
由式(4)的sinc(·)项可见,目标回波信号的包络随着慢时间发生变化,当包络变化超过一个距离单元(Δr=c/2B)时,会产生距离徙动。其中,包络中常数项不会对距离徙动造成影响,第二项产生距离走动,第三项导致距离弯曲。另外,考虑目标的加速度,式(4)的指数项为关于慢时间的LFM函数,指数项第二项引起多普勒频偏,第三项导致多普勒扩散。直接利用动目标检测(moving target detection, MTD)技术对目标相参处理,会导致信号能量散焦,降低目标积累增益。可见,距离徙动和多普勒徙动增大了目标信号的积累难度,为了提高积累性能,需要消除距离徙动和多普勒徙动。

2 本文算法原理

对式(4)进行距离维傅里叶变换,可得

(5)

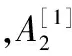
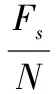
(6)

将式(6)代入式(5),得

(7)

式中,Fs为距离维采样率。由式(6)和式(7)可以看出,由于离散距离频率fr具有对称性,因此可以根据对称性将数据沿着距离维进行反转,即将数据沿着距离维倒序排列,反转之后的离散距离频率表示为

(8)

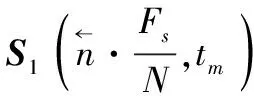
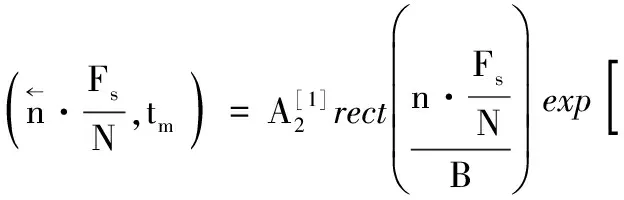
(9)

然后将两者相乘,示意图如图1所示。

图1 距离频率轴反转变换Fig.1 Range frequency axis reversal transform

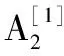
(10)

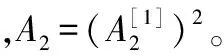
(11)

至此,完成了距离徙动校正,信号包络相对于慢时间tm为常数,即信号能量集中于一个距离单元。传统的距离徙动校正算法,如Keystone类算法和参数搜索类算法,都是对有限阶数(例如速度、加速度)的距离徙动进行校正,不能解决残留的高次项带来的影响,仅消除了部分距离频率fr与慢时间tm的耦合,存在一定的偏差。而本文所提出的距离徙动校正算法,通过距离频域的相关变换,完全消除了fr与tm之间的耦合,不局限于式(2)中的2阶项,可以对fr与任意阶tm解耦合,理论上实现精确的距离徙动校正。

距离徙动校正后,信号包络相对于tm为常数,因此式(11)可以表示为二阶相位函数

(12)

完成了距离徙动校正,下面利用参数估计的方法对多普勒徙动进行补偿。本文采用WVD变换核,对式(12)进行变换,表达式为

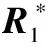
(13)

式中,上标*表示复共轭符号和时延;τ表示时延。

将式(12)代入式(13),得

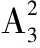
(14)

exp(-j2πξtmτf[ξτtm])·d(tmτ)=

(15)

T2(f[ξτtm],fτ)=FFTτ[T1(f[ξτtm],τ)]=

(16)

上述即为所提算法原理,因此,基于频率轴反转与GSCFT的机动目标检测与参数估计算法可以简写为

T2(f[ξτtm],fτ)=

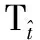
(17)

式中,GSCFT(·)表示式(15)中的广义尺度傅里叶变换;WVD(·)表示式(13)中利用WVD核函数进行自相关变换;FAR(·)表示式(10)中的频率轴反转变换。

利用本文算法对运动目标检测的流程图如图2所示。

图2 本文方法处理流程Fig.2 Processing steps of the proposed algorithm

3 计算复杂度分析

本文在计算复杂度方面与RFRFT[17]算法、两维频域匹配滤波算法[1]、Keystone算法、二阶WVD算法[26]和RFT算法进行对比。为了便于比较,假设距离维点数为N,方位维点数为M,对于速度和加速度的搜索次数均为L,通常情况下L大于N和M。

由图2可见,本文算法主要由WVD变换、GSCFT和沿着时延维的FFT构成。WVD运算量级为O(M2),GSCFT(通过chirp-z变换实现)运算量级为O(M2log2M),时延维FFT运算量级为O(M2log2M),因此总的运算复杂度仍然为O(M2log2M)。两维频域匹配滤波算法需要对加速度进行搜索,消除两维频域变量之间的耦合,所以运算复杂度为O(L(MNlog2M+MNlog2N)),运算复杂度要高于本文所提算法,而且两维频域匹配滤波算法在小时宽带宽积条件下不再适用。RFRFT算法需要对3个参数(距离单元、速度和加速度)进行搜索,因此计算复杂度为O(L3Mlog2M),运算量远大于本文所提算法。如果采用插值的方式进行处理,则Keystone算法的运算复杂度为O[N·M2],而且不能解决距离弯曲的问题。RFT需要对目标距离单元和速度进行搜索估计,计算复杂度为O(L2NM+NM·log2M)。二阶WVD算法主要由Keystone算法与两维FFT构成,因此计算复杂度为O[N·M2+M2log2M]。表1给出了6种算法的运算复杂度结果。表2给出了相同系统参数与目标仿真参数下(见表3与表4),6种算法的运行时间对比结果。(算法在Matlab R2015b运行,计算机配置为:Intel(R) Core(TM) 四核 i5-3570 (3.4 GHz), RAM为4 GB),可见,相比于其他5种方法,本文算法运算复杂度极低。

表1 计算复杂度对比

表2 运算时间对比

4 仿真实验与分析

本节在零均值复高斯白噪声背景下,通过点目标仿真实验来验证本文方法对运动目标聚焦的有效性。雷达系统仿真参数如表3所示。

表3 雷达系统参数

4.1 单目标仿真分析

首先分析单个目标的相参积累性能,目标运动参数如表所示。为了清楚体现本文方法处理过程,目标信噪比设为10 dB。图3(a)～图3(i)给出了本文方法与MTD和Keystone的运动目标处理结果。由图3(a)可见,原始数据距离脉压后,机动目标存在距离走动和弯曲现象。忽略目标距离徙动与多普勒徙动,将导致目标能量分散到多个距离单元,影响目标相参积累,MTD处理结果如图3(b)所示。图3(c)给出了基于频率轴反转变换距离徙动校正的结果,本文方法有效实现了机动目标的距离徙动校正,校正后的目标信号位于一个距离单元之内。图3(d)给出了对距离徙动校正后的数据做WVD变换的结果,由图可见,慢时间与时延存在耦合,因此需要对变换后数据(即式(14))进行GSCFT处理。图3(e)为GSCFT处理后的结果,可见,本文方法有效实现了调频率与时延的解耦合(即式(15))。

图3(f)给出了时延维FFT后的结果,调频率与中心频率已经在两维平面内聚焦,与式(16)相互对应。图3(g)为图3(f)的三维展示,通过峰值提取技术与式(16)的计算,得到估计的速度与加速度分别为99.95 m/s和49.925 m/s2,实际值分别为100 m/s和50 m/s2。图3(h)为最终目标聚焦结果,点目标已经精确聚焦。作为对比,图3(b)和图3(i)分别给出了MTD和Keystone的处理结果, 3种方法均出现了能量散焦,增大了目标检测难度。

表4 单目标运动参数

图3 单目标处理结果Fig.3 Simulation results for a moving target

4.2 多目标仿真结果

本小节进行基于本文方法的多目标仿真验证。雷达系统参数与第4.1节相同,目标运动参数如表5所示。图4给出多目标处理结果。由图4(a)可见,原始数据距离脉压后,两个机动目标均存在严重的距离走动和弯曲现象。图4(b)给出了基于频率轴反转变换距离徙动校正的结果,本文方法有效实现了多机动目标的距离徙动校正,校正后的目标信号位于一个距离单元之内。图4(c)为GSCFT处理后结果,本文方法实现了调频率与时延的解耦合,通过两维积累形成明显的峰值,具有良好的交叉项抑制性能。

表5 多目标运动参数

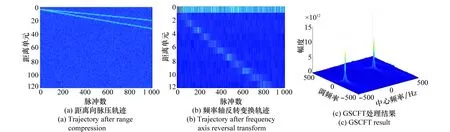
图4 多目标处理结果Fig.4 Simulation results for multiple targets

4.3 性能分析

4.3.1 目标参数估计性能分析

在本节中,分析所提算法在不同信噪比(signal-to-noise ratio, SNR)条件下的目标参数估计性能。为了便于分析,通过单目标仿真实验进行说明,雷达系统参数与目标运动参数分别如表3与表4所示,输入SNR(脉压后)分别取-10 dB,3 dB和20 dB。

图5给出了3个不同SNR下参数估计结果。图5(a)为SNR=-10 dB的处理结果,可见,此时不能正确估计出目标参数。图5(b)为SNR=3 dB的处理结果,速度与加速度估计值分别为99.85 m/s和50.05 m/s2。图5(c)为SNR=20 dB的处理结果,速度与加速度估计值分别为99.925 m/s和49.925 m/s2。实际值分别为100 m/s和50 m/s2。

图5 参数估计结果Fig.5 Processing results for parameters estimation

由图5可见,所提算法在低SNR条件下参数估计性能变差。本文算法的优势在于避免了繁琐的参数搜索操作,实现了非搜索的目标参数快速估计,运算量极低。但是快速是以牺牲目标输出信噪比为代价的,因为频率反转变换与WVD变换均为非线性变换,非线性变换会损失目标输出SNR,导致低信噪比条件下检测性能下降。所以,本文算法达到了计算复杂度与目标检测性能的折中。

4.3.2 检测性能分析

在本节中,利用恒虚警检测器,分析所提算法与目前典型算法在零均值复高斯白噪声背景下的检测性能。为了便于分析,通过单目标蒙特卡罗仿真实验进行说明,雷达系统参数与目标运动参数分别如表3与表4所示。令脉压后输入SNR变化范围为-5 dB到15 dB,步长为1 dB,每一个SNR进行100次蒙特卡罗实验。

图6为本文所提算法与RFRFT[17]、两维频域匹配滤波算法[1]、Keystone[9]、RFT[11]、二阶WVD[26]的检测概率随着输入SNR(脉压后)的变化结果,恒虚警率Pfa设为10-6。由图6可见,相同SNR条件下,本文所提算法的检测性能明显优于RFT,Keystone和二阶WVD算法,因为RFT与Keystone算法没有考虑加速度带来的影响,二阶WVD忽略了部分距离弯曲,并且两次相关操作会损失目标输出SNR。当SNR>1 dB时,所提算法检测性能优于两维频域匹配滤波算法,与RFRFT的工作性能曲线趋于一致。然而,RFRFT和两维频域匹配滤波算法均需要对参数搜索估计,计算复杂度高,本文所提算法不需要任何的参数搜索过程,运算复杂度远小于其他算法。

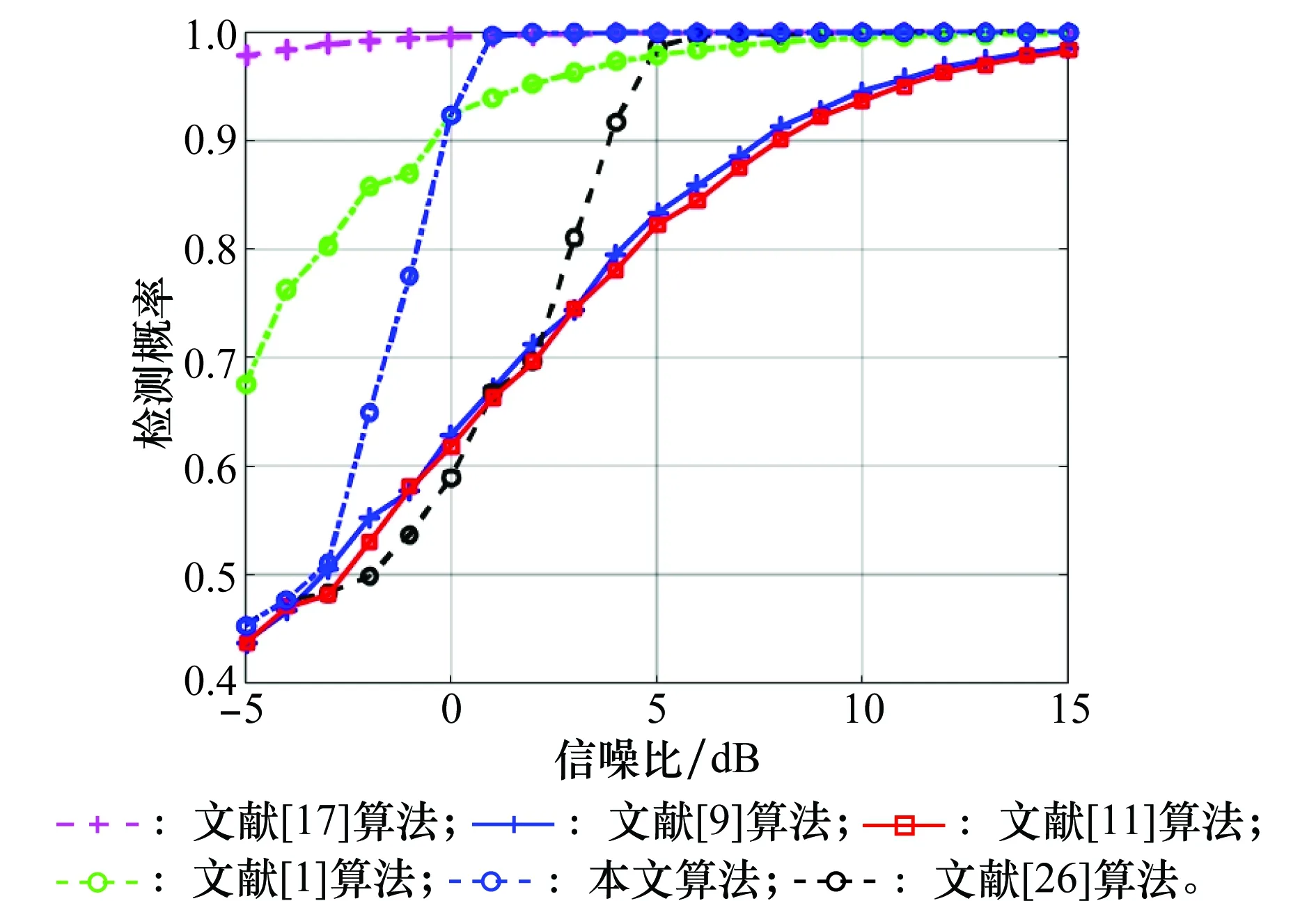
图6 检测概率Fig.6 Detection probability

5 结束语

机动目标回波信号在脉冲积累时间内发生的距离徙动和多普勒扩散现象,制约着雷达对运动目标的检测性能。本文讨论一种基于频率轴反转变换和GSCFT的运动目标检测方法。优点如下:①通过频率轴反转变换可以快速有效地消除距离徙动现象;②通过GSCFT可有效地抑制交叉项和改善参数模糊问题;③由于不需要对目标运动参数进行搜索估计,因此本文算法运算复杂度较低,便于工程实现。理论分析和仿真实验证明本文方法的有效性。针对低SNR环境下的机动目标参数快速估计,本文将在后续的工作中进一步展开研究。

[1] ZHU S Q, LIAO G S, YANG D. A new method for radar high-speed maneuvering weak target detection and imaging[J]. IEEE Geoscience and Remote Sensing Letter,2014,11(7):1175-1179.

[2] PANG C, TAO S, TAO R. Detection of high-speed and accelerated target based on the linear frequency modulation radar[J]. IET Radar, Sonar and Navigation, 2014, 8(1): 37-47.

[3] TIAN J, CUI W, WU S. A novel method for parameter estimation of space moving targets[J]. IEEE Geoscience and Remote Sensing Letter, 2014, 11(2): 389-393.

[4] SU J. High-speed multi-target detection with narrowband radar[J]. IET Radar, Sonar and Navigation, 2010, 4(4): 595-603.

[5] ZHENG J B, SU T, ZHANG L. ISAR imaging of targets with complex motion based on the chirp rate-quadratic chirp rate distribution[J]. IEEE Trans.on Geoscience and Remote Sensing, 2014, 52(11): 7276-7289.

[6] BAI X. ISAR imaging of a ship target based on parameter estimation of multicomponent quadratic frequency-modulated signals[J]. IEEE Trans.on Geoscience and Remote Sensing, 2014, 52(2): 1418-1429.

[7] KONG L J, LI X L, CUI G L. Coherent integration algorithm for a maneuvering target with high-order range migration[J]. IEEE Trans.on Signal Processing, 2015, 63(17): 4474-4486.

[8] TAO R. Analysing and compensating the effects of range and Doppler frequency migrations in linear frequency modulation pulse compression radar[J]. IET Radar, Sonar and Navigation, 2011, 5(1): 12-22.

[9] PERRY R P, DIPIETRO R C, FANTE R L. SAR imaging of moving targets[J]. IEEE Trans.on Aerospace and Electronic Systems, 1999, 35(1): 12-22.

[10] LI G, XIA X G, PENG Y N. Doppler keystone transform: an approach suitable for parallel implementation of SAR moving target imaging[J]. IEEE Geoscience and Remote Sensing Letter, 2008, 5(4): 573-577.

[11] XU J, YU J, PENG Y N. Radon-Fourier transform (RFT) for radar target detection (I): generalized Doppler filter bank processing[J]. IEEE Trans.on Aerospace and Electronic Systems, 2011, 47(2): 1186-1202.

[12] ZHOU F, WU R, XING M. Approach for single channel SAR ground moving target imaging and motion parameter estimation[J]. IET Radar, Sonar and Navigation, 2007, 1(1): 59-66.

[13] DING Y, XUE N. An analysis of time-frequency methods in SAR imaging of moving targets[C]∥Proc.of the Sensor Array and Multichannel Signal Processing Workshop,2000:221-225.

[14] LI X L. A fast maneuvering target motion parameters estimation algorithm based on ACCF[J]. IEEE Signal Processing Letters, 2015, 22(3): 270-274.

[15] LI X L. Fast non-searching method for maneuvering target detection and motion parameters estimation[J]. IEEE Trans.on Signal Processing, 2016, 64(9): 2232-2244.

[16] LI X L. Coherent integration for maneuvering target detection based on Radon-Lv’s distribution[J]. IEEE Signal Processing Letters, 2015, 22(9): 1467-1471.

[17] CHEN X L, GUAN J, LIU N B. Maneuvering target detection via Radon-fractional Fourier transform-based long-time coherent integration[J].IEEE Trans.on Signal Processing,2014,62(4): 939-953.

[18] GOLDEN S, BENJAMIN F. Maximum likelihood estimation, analysis, and applications of exponential polynomial signals[J]. IEEE Trans.on Signal Processing, 1999, 47(6): 1493-1501.

[19] ANGEBY J. Estimating signal parameters using the nonlinear instantaneous least squares approach[J]. IEEE Trans.on Signal Processing, 2000, 48(10): 2721-2732.

[20] WANG P, LI H B. Integrated cubic phase function for linear FM signal analysis[J]. IEEE Trans.on Aerospace and Electronic Systems, 2010, 46(3): 963-977.

[21] PORAT B, BENJAMIN F. Asymptotic statistical analysis of the high-order ambiguity function for parameter estimation of polynomial-phase signals[J]. IEEE Trans.on Information Theory, 1996, 42(3): 995-1001.

[22] XIA X G. A quantitative analysis of SNR in the short-time Fourier transform domain for multicomponent signals[J]. IEEE Trans.on Signal Processing, 1998, 46(1): 200-203.

[23] XIA X G, CHEN V C. A quantitative SNR analysis for the pseudo Wigner-Ville distribution[J]. IEEE Trans.on Signal Processing, 1999, 47(10): 2891-2894.

[24] HUANG P. Ground maneuvering target imaging and high-order motion parameter estimation based on second-order keystone and generalized hough-haf transform[J]. IEEE Trans.on Geoscience and Remote Sensing, 2017, 55(1): 320-335.

[25] ZHENG J, LIU H, LIAO G. ISAR imaging of targets with complex motions based on a noise-resistant parameter estimation algorithm without nonuniform axis[J]. IEEE Sensors Journal, 2016, 16(8): 2509-2518.

[26] HUANG P. Fast SAR imaging method for ground moving target using SOWVD transform[J]. IEEE Trans.on Geoscience and Remote Sensing, 2016, 54(4): 320-335.