流体力学仿真软件可信度评估与预测能力
王瑞利++梁霄++喻强

摘要: 针对爆轰流体力学过程的控制方程和辅助方程,剖析模型参数、模型形式和数值方法等的不确定因素,列举爆轰流体力学模型的不确定性因素并开展敏感度分析。针对几个重要参数,发展高维参数抽样技术,结合爆轰产物JWL状态方程的圆筒试验,开展自主研发的爆轰弹塑性流体动力学LAD2D仿真软件的可信度评估研究,给出可信度评估结果。此方法和研究思路为复杂工程仿真软件可信度评估提供一种有效手段。
关键词: 爆轰过程; 唯象模型; 数值模拟; 不确定性量化; 敏感度分析; 高维抽样
中图分类号: TB115.1文献标志码: B
Confidence evaluation and prediction ability of
hydrodynamics simulation software
WANG Ruili1, LIANG Xiao2, YU Qiang3
(1. Beijing Institute of Applied Physics and Computational Mathematics, Beijing 100094, China;
2. College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao 266590,
Shandong, China; 3. Beijing Anwise Technology Co., Ltd., Beijing 100022, China)
Abstract: As to the control equations and auxiliary equations of detonation fluid dynamics, the uncertain factors, such as the model parameters, the model form, and numerical methods, are analyzed, the uncertainty factors of detonation fluid dynamics model are listed, and their sensitivities are analyzed. Focusing on several important parameters, the high dimension parameter sampling method is developed. The reliability evaluation of the LAD2D software for the simulation of detonation fluid dynamics is carried out by combing with the JWL equation of state in the cylinder test. The reliability evaluation results are given finally. The method and research idea provides a very effective technology for evaluating the credibility of complex engineering simulation software.
Key words: detonation process; phenomenological model; numerical simulation; uncertainty quantification; sensitivity analysis; high dimension sampling
收稿日期: 2017[KG*9〗08[KG*9〗24修回日期: 2017[KG*9〗08[KG*9〗29
基金项目: 国家自然科学基金(11372051,91630312,11475029);国防基础科研计划(C1520110002);
中國工程物理研究院科学基金(2015B0202045)
作者简介: 王瑞利(1964—),男,研究员,研究方向为计算流体力学及其应用软件,(Email)wang_ruili@iapcm.ac.cn0引言
高能炸药爆轰和可燃气体燃烧爆炸过程都是多尺度、多物理场耦合的复杂系统,涉及高温、高压、高速以及材料相变等多种介质相互作用、相互混合,使理论和实验研究困难增大。[12]为此,国家高端领域复杂系统可靠性认证、大型装置性能评估和民用设备意外爆炸事故分析与预防等成为科学难题和瓶颈。随着计算机技术的快速发展,高置信度建模、高可信度应用软件开发与数值仿真技术逐渐弥补理论和实验的缺陷,成为理论、实验、模拟与科学、技术和工程相关领域交叉研究的重要课题。复杂系统的数值仿真技术是信息时代世界各国特别是发达国家激烈竞争的技术制高点,是一个国家综合国力、科技创新力和国防装备战斗力的重要标志,是未来提高武器装备研制的有效手段。但是,高能炸药爆轰和可燃气体燃烧爆炸过程具有瞬态性,其在极短时间内剧烈变化且各种因素相互耦合,难以独立(分解)处理,理论和实验难度都很高。基于对此类问题认知的缺陷,很多研究只能针对所关心的重大核心问题,忽略次要因素,通过适当的简化处理,建立适于解决某一问题的物理模型或唯象模型,探寻不断完善、逐渐逼近实际的数值仿真技术。这些研究方法最大的缺陷是由于模型参数、模型形式、逼近方法等众多不确定性融合在一起形成的强不确定性或模拟预测结果的随机性。[34]因此,国防安全领域中先进新型武器设计、现役武器维护、退役武器处理、可燃气体爆炸等数值仿真技术都面临强不确定性或随机性的挑战,现有方法和技术还不能处理此类强不确定性问题,亟待有所突破与创新。近几年,美国从国家层面推出ASC等系列计划,其目的是推动数字化设计和计算能力的提升,应对来自其他国家的竞争压力。验证与确认已成为提高可信度的最佳途径,其最大瓶颈仍是模型参数、模型形式、逼近方法等众多因素融合在一起的强不确定性,严重影响仿真软件的可信度。[57]中国亟需从战略高度认识到国防或CAE领域数值仿真技术中强不确定性量化和可信度评估的重要性。实际上,不论在实际生活还是科学研究中,研究人员都会面临对某些系统的运行性能进行评价,得到的评价结果对妥善使用系统或者改进系统至关重要。endprint
1爆轰流体动力学模型及其不确定性
1.1爆轰流体力学物理模型
爆轰流体力学物理模型是由双曲型的流体力学(偏微分方程组)与炸药唯象反应率模型(一阶常微分方程)、物态方程(复杂函数关系式)耦合在一起的非线性偏微分方程组。
2.2基于圆筒试验的爆轰模型多因素敏感度分析
圆筒试验结构示意和计算模型见图1。炸药取TNT炸药,性能参数为γT=3.1,ρT=1.634 g/cm3,DCJ=6.932 km/s;紫铜物理性能参数为γC=3.68,ρC=8.93 g/cm3,c=3.94 km/s。在O点起爆或者面爆,炸药采用JWL状态方程和Wilkins反应率模型,紫铜采用Gruneisen状态方程和SG本构模型。对每个因素采用抽样技术,然后将其输入到自主研发的确定性软件LAD2D[11]中,产生敏感度分析响应量的样本。各因素样本计算值见表2。计算参数除因素栏说明外,其余均按统一计算条件取值:JWL参数取R1=4.6,R2=1.3,ω=0.38;燃烧函数中的参数取nb=1.3,rb=2.1,采用压缩比起爆时取σ=1.03,采用时间起爆时按惠更斯原理预先计算起爆时间。
基于上述样本数据,爆轰压力、爆轰速度和爆轰位置的敏感性分析结果见图2。各因素对爆轰压力、爆轰位置影响的敏感性差异不大,而对爆轰速度敏感性差别比较大。将12个因素按速度敏感性进行排序,见表3。从图2和表3可以看出,对于爆轰模型,各影响因素的敏感性大小排序为:时间起爆燃烧下γb,体积起爆燃烧下γb,时间起爆下JWL ω,体积起爆燃烧下nb,时间起爆下JWL R1,体积起爆下JWL ω,体积起爆下JWL R2,时间起爆下JWL R2,体积起爆下JWL R1,时间起爆燃烧下nb,体积起爆阈值σ,起爆方式。由此可知,燃烧函数和JWL产物状态方程是2个敏感性强的模型。为此,需要重视其参数选取及模型形式。a) 爆轰压力3产物状态方程不确定性量化及软件可信度评估通过上述敏感性分析可以看出在爆轰物理模型和数值模拟中哪些因素“很敏感”或“很关键”,针对“很敏感”因素开展不确定性量化,以评估仿真软件的可信度。这里选取炸药爆轰产物JWL状态方程的唯象模型形式中的不确定参数为不确定度量化对象。
3.1产物状态方程参数区间抽样产生有效样本
由于JWL状态方程中参数A,B,C依赖于参数R1,R2,w,为此,表征或标定参数R1,R2,w非常重要。对于大多数炸药,凭先验估计这3个参数属于认知不确定度,R1∈[4.0,5.0],R2∈[1.0,2.0],w∈[0.2,0.4]。基于拉丁方抽样方法,本文发展高维抽样技术,即ξi=a+Δx·θ,对R1,R2,w这3个不确定性参数进行抽样,其中100组样本和1 000组样本抽样结果见图3。
考虑到爆轰产物的压力恒为正,则有不等式约束条件A>0且B>0且C>0。根据此约束条件,以JOB9003炸药为例[12],从物理层面上判断样本的有效性。JOB9003炸药的物理性能参数为ρ0=1.849 g/cm3,k=2.99,DCJ=8.712 km/s。由A,B和C参数与R1,R2和w参数的线性方程组[3],可计算出A,B和C这3个参数,再通过A>0,B>0,C>0,就能判断样本的有效性。参数R1,R2和w在100组样本点和1 000组样本点中的有效样本见图4。在100组样本中有81组样本有效,在1 000组样本中有840组样本有效。有效样本求出的参数A,B和C见图5。图中为A>0,B>0,C>0的有效样本,满足物理要求。
3.2响应量径向壁位置和速度
在众多爆轰产物状态方程的形式中,JWL状态方程是一种不显含化学反应、由试验方法确定参数的半经验状态方程,能比较精确地描述爆轰产物的膨胀驱动做功过程。圆筒试验是指将炸药放入等壁厚的铜质圆筒中,从圆筒的一端将其引爆,利用高速转镜式扫描相机记录筒壁在爆轰产物驱动下的膨胀过程,是确定炸药爆轰产物JWL状态方程和评估炸药做功能力的标准化试验,国内外广泛应用。圆筒试验布局见图6,采用狭缝扫描和VISAR联合测试方法。主炸药以JOB9003为例,直径为25.4 mm,长度为305.0 mm;圆筒内径为25.4 mm,壁厚为2.6 mm,材料为紫铜。狭缝扫描采用平行光后照明技术,狭缝位置距离起爆端200.0 mm。相机转速为6×104 r/min,对应的扫描速度为3 km/s。VISAR测试与狭缝扫描光路垂直,光纤探头前段距装置外表面75.0 mm,光路与静态装置外表面垂直。VISAR测试位置与狭缝扫描位置对应,距起爆端200.0 mm。同时,在圆筒末端的定常滑移爆轰段采用电探针法测定炸药爆速。[1213]
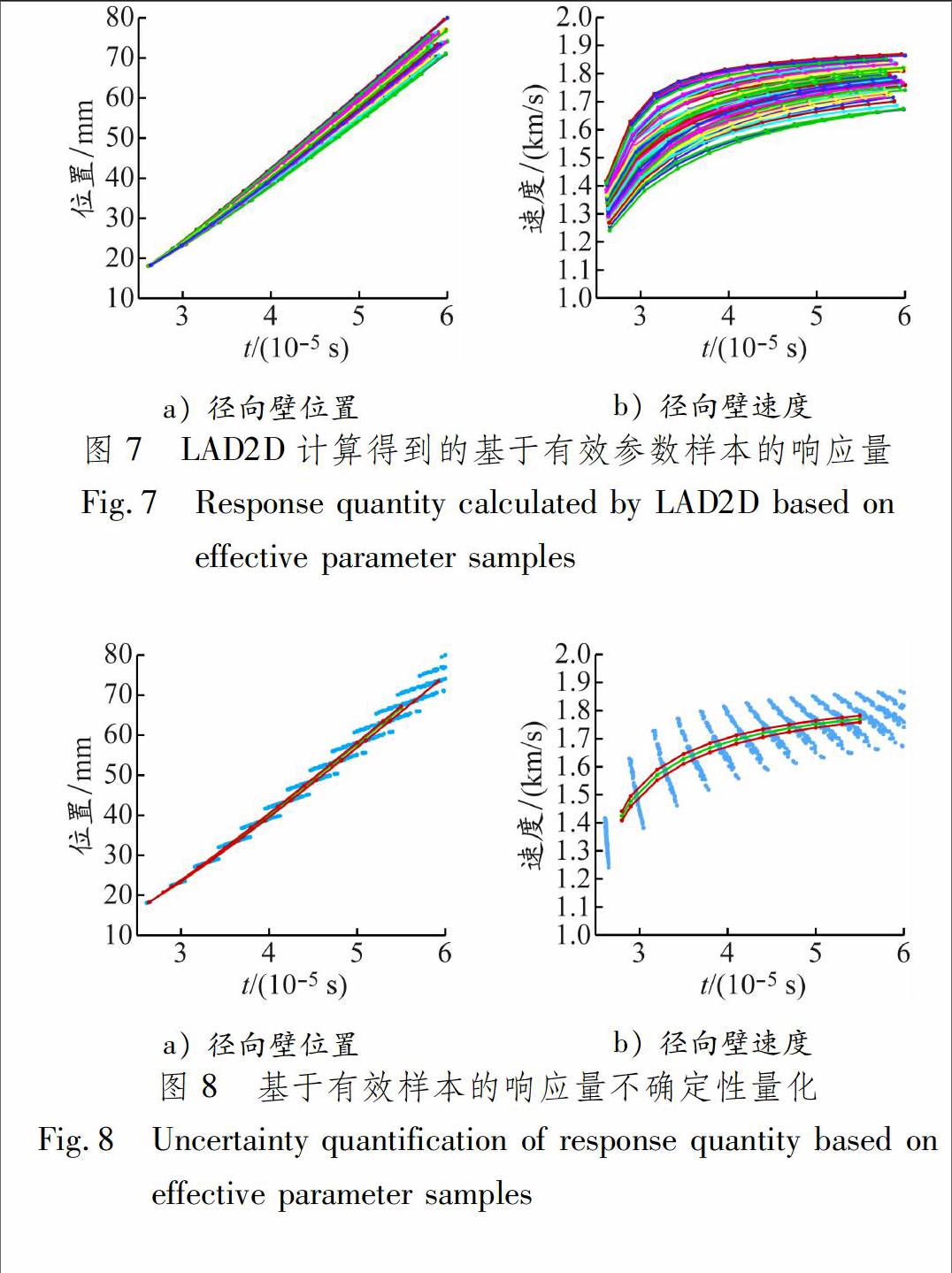
在参数R1,R2和w的样本点上进行确定性数值计算时采用LAD2D软件。[11]LAD2D是北京应用物理与计算数学研究所自主开发的大型爆轰弹塑性流体动力学程序,空间离散采用拉氏有限体积格式,能够准确捕捉自由面速度,时间离散采用预报校正方法。计算过程采用能够有效处理拉氏计算过程中网格大变形问题的网格邻域可变技术。为有效模拟激波传播及其相互作用的问题,采用人工黏性方法,综合考虑流体弹塑性和炸藥反应过程。大量数值模拟计算结果表明,LAD2D具有较为完整的解决工程实际问题的模拟能力。在81组有效样本上模拟计算圆筒试验,得到离起爆端200.0 mm狭缝面的径向壁位置和速度曲线,见图7。
a) 径向壁位置b) 径向壁速度图 7LAD2D计算得到的基于有效参数样本的响应量
3.3JWL状态方程不确定性量化及可信度评估
基于上述响应量的样本,通过统计方法,得到位置与速度随时间演变的期望与方差。参数R1,R2和w的不确定性对圆筒试验离起爆端200.0 mm狭缝处径向壁位置和速度传播的影响见图8。从图7可以看出,响应量(径向壁位置和径向壁速度)分散度比较大。采用多项式混沌方法给出的模拟结果的不确定性见图8,将其与确认试验(含有不确定性评估)的测试数据对比,就可以给出模型和软件的可信度。同时,采用贝叶斯原理[1415],可反推给出爆轰唯象模型的可信参数,达到高置信度的预测能力。endprint
a) 径向壁位置b) 径向壁速度图 8基于有效样本的响应量不确定性量化
Fig.8Uncertainty quantification of response quantity based on effective parameter samples
3.4Wilkins反应率不确定性量化及可信度评估
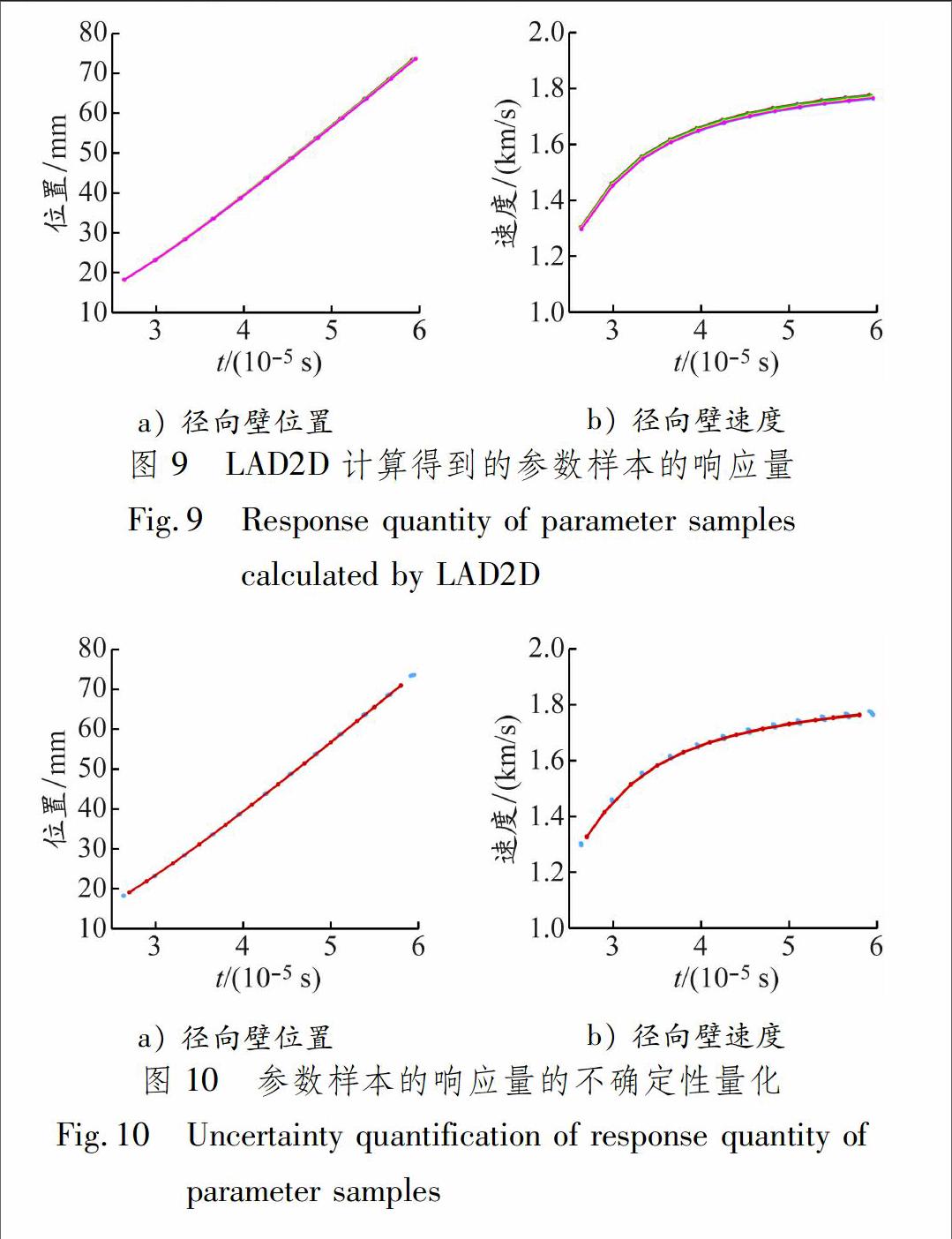
针对Wilkins反应率唯象模型中的参数nb和rb,凭先验估计,这2个参数属于认知不确定度,nb∈[1.0,6.0],γb∈[2.0,3.0],基于拉丁方抽样方法给出30个样本。对应的狭缝径向壁位置和速度的模拟结果见图9,采用统计分析方法给出模拟结果的不确定性量化见图10。
a) 径向壁位置b) 径向壁速度图 9LAD2D计算得到的参数样本的响应量
从图9和10可以看出,Wilkins反应率唯象模型分散度比JWL状态方程小,说明此模型不确定性小。
4结束语
针对炸药爆轰唯象模型(爆轰产物JWL状态方程)中的不确定性参数,通过拉丁方抽样技术,并结合爆轰流体力学软件LAD2D開展圆筒试验计算,建立不确定性参数与响应量的样本,通过贝叶斯理论,校准与确认计算模型的参数。
本文只是尝试模型确认的思路,通过实验说明其可行性。在复杂工程建模与模拟中,不确定性涉及内容较多,需要开展大量研究工作,应引起工程仿真学者的高度重视。
针对国防或CAE领域机理建模与模拟中强不确定性现象密切相关的科学规律、数学方法与理论,发展复杂工程仿真软件可信度评估方法及应用的前沿核心技术,突破数值仿真技术未考虑不确定性的桎梏,建立国防或CAE领域复杂系统数值模拟技术中强不确定性高效量化方法及分析软件,发展一批强预测能力的仿真软件,是未来国防或CAE领域发展的重要方向。
参考文献:
[1]孙锦山, 朱建士. 理论爆轰物理[M]. 北京: 国防工业出版社, 1995.
[2]王瑞利, 梁霄. 爆轰数值模拟中物理模型分层确认实验研究[J]. 中国测试, 2016, 42(10): 1320.
WANG R L, LIANG X. Research on validation experiment hierarchy of validation for physical modeling in numerical simulation of detonation[J]. China Measuement & Testing Technology, 2016, 42(10): 1320.
[3]王瑞利, 江松. 多物理耦合非线性偏微分方程与数值解不确定度量化数学方法[J]. 中国科学: 数学, 2015, 45(6): 723738. DOI: 10.1360/N01201400115.
WANG R L, JIANG S. Mathematical methods for uncertainty quantification in nonlinear multiphysics systems and their numerical simulations[J]. Science China: Math, 2015, 45(6): 723738. DOI: 10.1360/N01201400115.
[4]OBERKAMPF W L, ROY C J. Verification and validation in scientific computing[M]. Cambridge: Cambridge University Press, 2010.
[5]王瑞利, 温万治. 复杂工程建模和模拟的验证与确认[J]. 计算机辅助工程, 2014, 23(4): 6168. DOI: 10.13340/j.cae.2014.03.013.
WANG R L, WEN W Z, Advances in verification and validation of modeling and simulation of the complex engineering[J]. Computer Aided Engineering, 2014, 23(4): 6168. DOI: 10.13340/j.cae.2014.03.013.
[6]邓小刚, 宗文刚, 张来平, 等. 计算流体力学中的验证与确认[J]. 力学进展, 2007, 37(2): 279288.
DENG X G, ZONG W G, ZHANG L P, et al. Verification and validation in computational fluid dynamics[J]. Advances in Mechanics, 2007, 37(2): 279288.
[7]王瑞利, 刘全, 温万治. 非嵌入式多项式混沌法在爆轰产物JWL参数评估中的应用[J]. 爆炸与冲击, 2015, 35(1): 915.
WANG R L, LIU Q, WEN W Z. Nonintrusive polynomial chaos methods and its application in the parameters assessment of explosion product JWL[J]. Explosion and Shock Waves, 2015, 35(1): 915.
[8]梁霄, 王瑞利. 爆轰流体力学模型敏感度分析与模型确认[J]. 物理学报, 2017, 66(11): 116401. DOI: 10.7498/aps.66.116401.endprint
LIANG X, WANG R L. Sensitivity analysis and validation of detonation computational fluid dynamics model[J]. Acta Physica Sinica, 2017, 66(11): 116401. DOI: 10.7498/aps.66.116401.
[9]HELTON J C. Conceptual and computational basis for the quantification of margins and uncertainty: SAND20093055[R].
[10]KARNIADAKIS G E, GLIMM J. Preface: uncertainty quantification in simulation science[J]. Journal of Computational Physics, 2006, 217(1): 14.
[11]王瑞利, 林忠, 溫万治, 等. 多介质拉氏自适应流体动力学软件LAD2D研制及其应用[J]. 计算机辅助工程, 2014, 23(2): 17.DOI: 10.13340/j.cae.2014.02.001.
WANG R L, LIN Z, WEN W Z, et al. Development and application of adaptive multimedia Lagrangian fluid dynamics software LAD2D[J]. Computer Aided Engineering, 2014, 23(2): 17.DOI: 10.13340/j.cae.2014.02.001.
[12]徐辉, 孙占峰. 钝感高能炸药JB9014做功能力的实验研究[J]. 高压物理学报, 2013, 27(4): 582586.
XU H, SUN Z F. An experimental study on the capacity for work of insensitive high explosive[J]. Chinese Journal of High Pressure Physics, 2013, 27(4): 582586.
[13]于川, 刘文翰, 李良忠, 等. 钝感炸药圆筒试验与爆轰产物JWL状态方程研究[J]. 高压物理学报, 1997, 11(3): 227233.
YU C, LIU W H, LI L Z, et al. Studies on cylinder test and JWL equation of state of detonation product for insensitive high explosive[J]. Chinese Journal of High Pressure Physics, 1997, 11(3): 227233.
[14]颜王吉, 曹诗泽, 任伟新. 结构系统识别不确定性分析的Bayes方法及其进展[J]. 应用数学和力学, 2017, 38(1): 4459.
YAN W J, CAO S Z, REN W X. Uncertainty quantification for system identification utilizing the Bayes theory and its recent advances[J]. Applied Mathematics and Mechanics, 2017, 38(1): 4459.
[15]何炎高, 徐定华, 陈瑞林. 纺织材料设计反问题的贝叶斯统计推断方法[J]. 纺织学报, 2015, 36(1): 2329.
HE Y G, XU D H, CHEN R L. Bayesian statistical inference method for inverse problems of textile material design[J]. Journal of Textile Research, 2015, 36(1): 2329.(编辑武晓英)第26卷 第6期2017年12月计 算 机 辅 助 工 程Computer Aided EngineeringVol.26 No.6Dec. 2017endprint

