两个广义伽玛分布之间的相对熵及其性质

朱成莲

0 引言

1951年,统计学家Kullback和Leibler提出了相对熵的概念，用来度量两个分布之间的差异程度，也称为Kullback-Leibler距离。在数理统计中,统计推断的一个重要方面就是从已知样本去估计母体的分布,或者推断分布的特征,对于同样的母体分布，当用几种不同的统计方法获得了母体的不同估计分布后,人们往往要对所求得的分布进行比较，为此，统计学上引入了许多度量两个分布差异的方法，如相对熵，Pearson-χ2距离和全变差距离等，相对熵应用于许多领域，从相对熵的定义看出，它已经不满足传统的距离中对称性、三角不等式性等条款。尽管如此，由于它确实能够在某种程度上刻画两个密度函数的差异程度，近年来，概率密度函数的相对熵在学术界备受关注，人们在讨论极值分布的大样本问题、分布函数估计的收敛性、用不同算法借补有缺失数据的分布估计的收敛速度等问题时，都使用相对熵[1-5]。本文将相对熵定义进行了推广，定义了最小相对熵。从定义形式上看，并不难理解，最小相对熵是将两个概率密度函数间的相对熵求较小值，但它的意义在于克服了相对熵没有对称性的缺陷。本文计算了两个广义伽玛分布之间相对熵及最小相对熵。作为广义伽玛分布的特例，推导出两个伽玛分布、Weibull分布、Rayleigh分布、正态分布、指数分布之间的相对熵及最小相对熵。

1 相关定义及其性质

则称随机变量X服从广义伽玛分布,记为GΓ()α，β，λ。

由定义1可知，当α，β取一些特殊值时，得到以下一些特例：

定义1[6]：如果随机变量X的概率密度函数为：

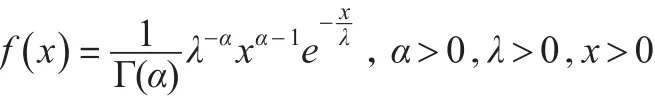
一般记为Γ(α，λ)。伽玛分布中，若α为整数就是Erlang分布；伽玛分布中，α=n（1）当β=1时，得到伽玛分布,密度函数为：2，λ=2就是 χ2分布。（2）当α=1时，得到Weibull分布,密度函数为：

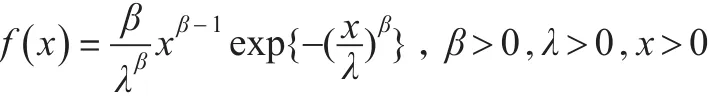
一般记为W(β，λ)。

（3）当 α=1，β=2，λ=2σ 时，得到 Rayleigh分布,密度函数为：

一般记为 R(σ)。

（4）当α=1，β=1时，得到指数分布，密度函数为：

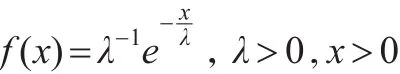
一般记为 E(λ)。

一般记为 N(0，σ2)。

定义 2[7]：设 f(x),g(x)是两个密度函数,Sf和Sg分f(x) dx＜+∞时,则称这个值是g(x)到f(x)的相对熵，又称为Kullback-Leibler距离,记为d( f ，g )。

当f(x)，g(x)都是离散型随机变量分布时，定义2中的积分需换成相应的求和记号。

定义3：设两个随机变量 X1，X2的概率密度函数分别为 f(x)、g(x)，并且 f(x)＞0，g(x)＞0，若 d( f ，g ) 和d(g，f)都存在，记 dmin(f，g)=min{d(f，g)，d(g，f)} ，则称dmin(f，g)为 f(x)，g(x)两个密度函数之间的最小相对熵。

由定义2和定义3易得以下有关相对熵的性质。

性质1：设 f(x)＞0，g(x)＞0是两个概率密度函数，则：

（1）非负性 d(f，g)≥0

（3）d(f，g)=0⇔E(lnf(x))=E(lng(x))⇔f(x)=g(x)=0

（4）d(f，g1)-d(f，g2)=

从性质1的（1）、（3）知相对熵确实能刻画两个分布g(x)与Sf之间的差异程度，但是相对熵对称性,三角形不等式未必成立。

性质2：设 f(x)＞0，g(x)＞0是两个概率密度函数，

则：

从性质2可以看出,最小相对熵与相对熵相比较,最小相对熵除了具有相对熵的性质外,还具有对称性、三角不等式性质。

引理1：如果随机变量X的概率密度函数为：

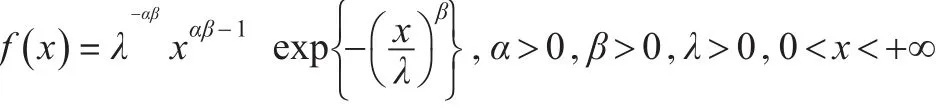
则：

证明：计算积分

由式（1）可得随机变量X的K阶矩为：

当式（1）中 s=0时，得到：

对式（2）两边关于α求导得：

因此：

2 两个广义伽玛分布之间的相对熵

定理 1：设 f(x)、g(x)分别是广义伽玛分布GΓ(α，β，λ1) 、GΓ(α，β，λ2)的密度函数,则：

证明：根据定义2可得：

所以：

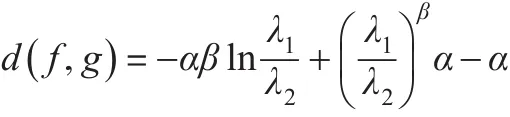
从上式可看出，当 λ1→λ2时，d(f，g)→0

定理 2：设f(x ) 、g(x)分别是广义伽玛分布GΓ(α，β，λ1) 、GΓ(α，β，λ2)的密度函数，则：

定理 3：设f(x ) 、g(x)分别是广义伽玛分布GΓ(α，β，λ1) 、GΓ(α，β，λ2)的密度函数，则：

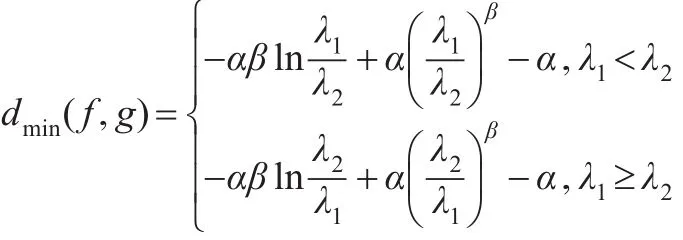
证明：由定理1和定理2可知：

构造函数：

可得：

易知 f(t)为(0，+∞ )单调递增函数。且当t=1时：

故：

因此：

且当 λ1→λ2时，d(f，g)→0 。

定理4：设 f(x)、g(x)分别是广义伽玛分布GΓ(α1，β，λ)、GΓ(α2，β，λ)的密度函数，则：′

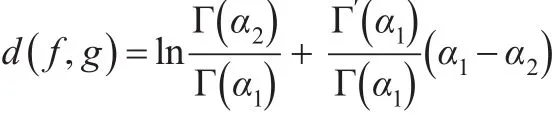
证明：根据相对熵的定义得：

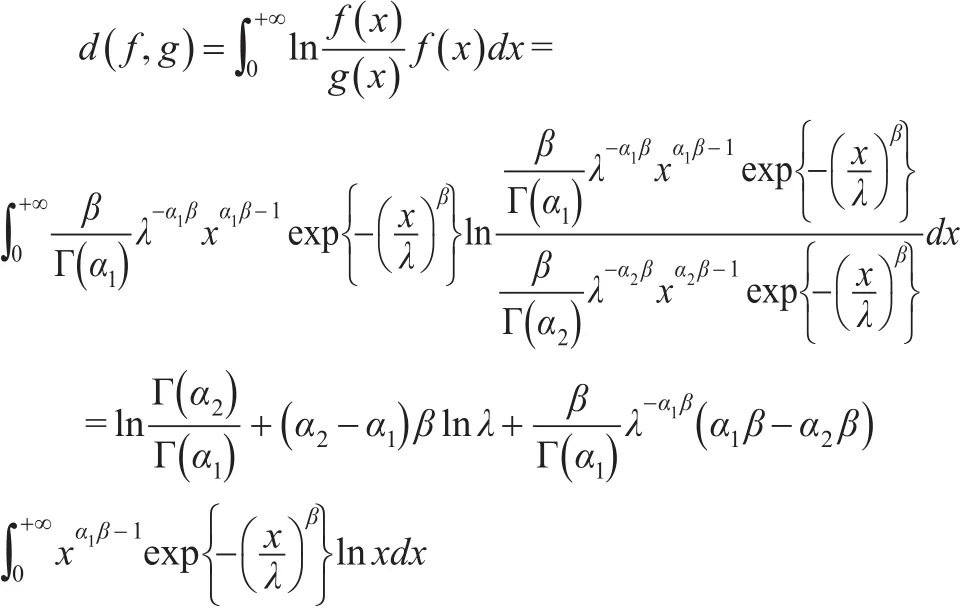
根据引理1结论可得：

所以：

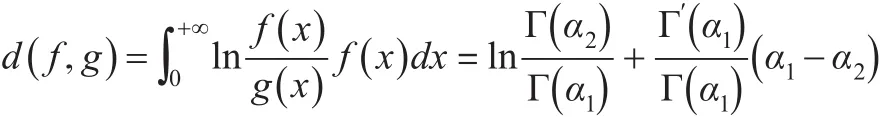
由上式可知，d( f ，g )与λ、β无关，两个密度函数的相近程度由参数α决定，当α1→α2时，d( f ，g )→0。

定理 5：设 f(x)、g(x)分别是广义伽玛分布GΓ(α1，β，λ)、GΓ(α2，β，λ)的密度函数，当 β ，λ确定时，

且当α1→α2时，d( f ，g )→0。

定理 6：设 f(x)、g(x)分别是广义伽玛分布GΓ(α，β1，λ)、GΓ(α，β2，λ)的密度函数，当 α ，λ确定时，

证明：根据相对熵的定义可得：

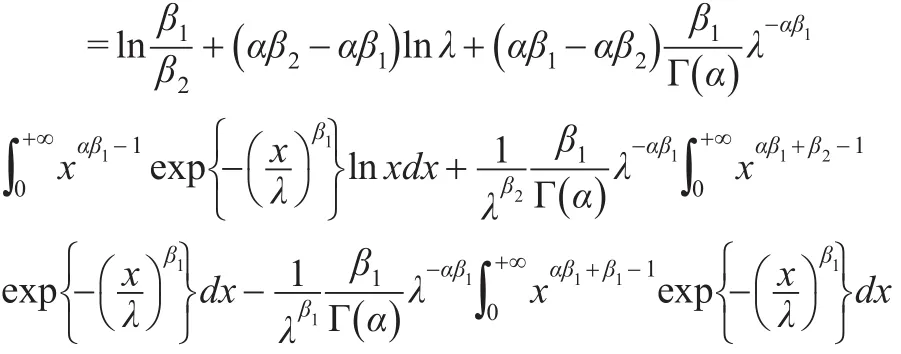
分别计算上式三个积分，根据引理1结论可得：

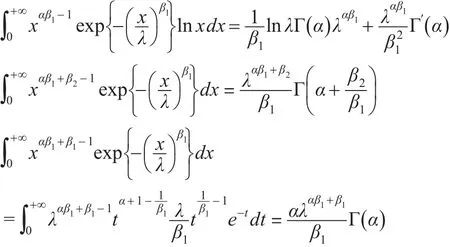
所以：

从上式可看出，d( f ，g ) 与 λ无关，当 β1→β2时，d(f，g)→0 。

定理 7：设f(x ) 、g(x)分别是广义伽玛分布GΓ(α，β1，λ)、GΓ(α，β2，λ)的密度函数,当 α ,λ确定时,则：

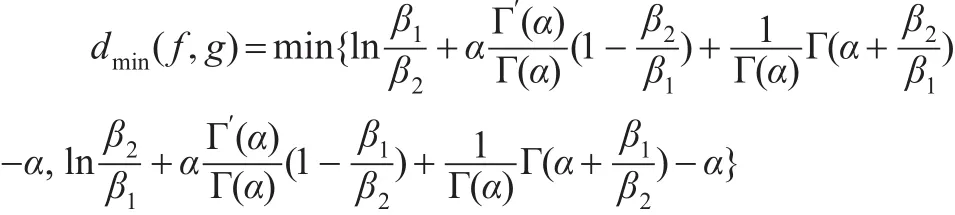
且当 β1→β2时，d(f，g)→0 。

由以上定理可得以下推论：

推论1：设 f(x)、g(x) 分别是伽玛 Γ(α，λ1) Γ(α，λ2)的密度函数，则：

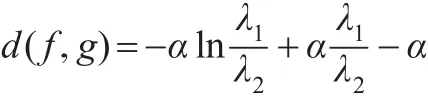
且当 λ1→λ2时，d(f，g)→0

推论2:设 f(x)、g(x) 分别是伽玛 Γ(α，λ1) Γ(α，λ2)的密度函数,则：

且当 λ1→λ2时，d(f，g)→0

推论3：设 f(x)、g(x )分别是Weibull分布W(β，λ1)、W(β，λ2)的密度函数，则：

且当 λ1→λ2时，d(f，g)→0。

推论4：设 f(x)、g(x )分别是Weibull分布W(β，λ1)、W(β，λ2)的密度函数，则：

且当 λ1→λ2时，d(f，g)→0 。

推论5：设 f(x)、g(x) 分别是 Rayleigh分布 R(σ1)、R(σ2)的密度函数，则：

且当σ1→σ2时，d(f，g)→0。

推论6：设 f(x)、g(x) 分别是 Rayleigh分布 R(σ1)、R(σ2)的密度函数，则：

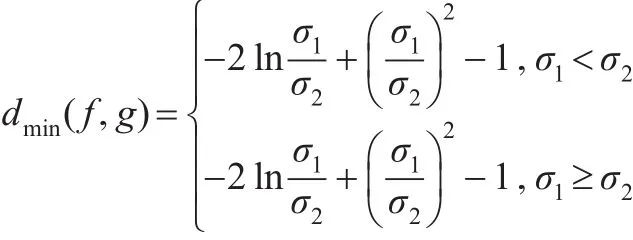
且当σ1→σ2时，d(f，g)→0。

且当σ1→σ2时，d(f，g)→0。

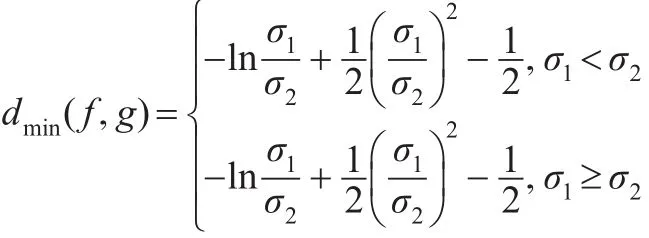
且当σ1→σ2时，d(f，g)→0。

推论9：设 f(x)、g(x) 分别是指数分布 E(λ1)、E(λ2)的密度函数，则：

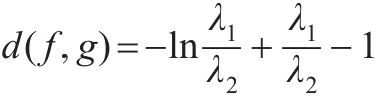
且当 λ1→λ2时，d(f，g)→0 。

推论10：设 f(x)、g(x) 分别是指数分布 E(λ1)、E(λ2)的密度函数，则：且当 λ1→λ2时，d(f，g)→0 。

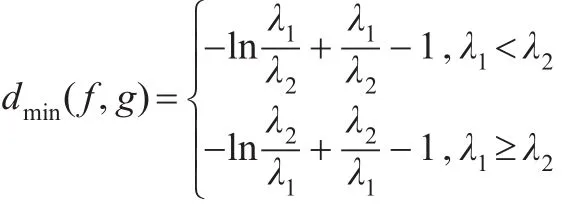
3 几个距离间的关系

定义4［7］：设 f(x)，g(x)是两个密度函数，Sf和Sg分离，记为 d2(f，g)。

定义 5［7］：设 f(x)，g(x)是两个密度函数，称V2(f，g)=suAp|F(A)-G(A)|是f(x)到g(x)的全变差距离，其中

定理8［7］：以下讨论的距离都存在，则：

（1）当 f(x)≥g(x)时，d(f，g)≤d2(g，f)。

（2）V2(f，g)≤ d2(f，g)。

有 d(f，g)，d(g，f)及 min{d(f，g)，d(g，f)} 的定义易得如下定理。

定理9：若以下讨论的距离都存在，则：

（1）min{d(f，g)，d(g，f)} ≤d(f，g)≤ max{d(f，g)，d(g，f)} ；

（2）当 f(x)≥g(x)时 d(f，g)≥d(g，f)，且 d(f，g)≥(d(f，g)+d(g，f))≥d(g，f) ；当f(x)≤g(x) 时 d(f，g)≤d(g，f)，且 d(f，g)≤(d(f，g)+d(g，f))≤d(g，f)。

从定理 9中的式（1）还可以看出，当 min{d(f，g)，d(g，f)}充分小时，必有d(f，g)充分小。用最小Kullback-Leibler距离min{d(f，g)，d(g，f)} 来比较两个密度函数比用d(f，g)刻画要合理。

4 结束语

相对熵用来度量两个分布之间的差异程度，相对熵越小，表示两个分布之间越接近，反之，相差越大，当两个分布相同时，相对熵为零。本文计算了两个广义伽玛分布之间的相对熵，得到了公式。根据参数的大小，非常容易度量两个广义伽玛分布之间接近程度，或根据两个广义伽玛分布之间接近程度的要求，由公式快捷选择参数。从相对熵的定义看出，它不满足传统的距离中对称性、三角不等式性等条款。本文定义了最小相对熵。从定义形式上看，并不难理解，最小相对熵是将两个概率密度函数间的相对熵求较小值，但它的意义在于克服了相对熵没有对称性的缺陷。并且最小相对熵充分小时，必有相对熵充分小。用最小相对熵来度量两个密度函数比用相对熵刻画更为合理。本文还推导出两个伽玛分布、Weibull分布、Rayleigh分布、正态分布、指数分布之间的相对熵及最小相对熵。为实际应用，提供许多方便。

[1]Robert G O,Shau S K.Updating Schemes,Correlation Structure,Blocking and Parameterization for the Gibbs Sampler[J].J R Statist Soc B,1997,(59).

[2]Liu S J,Wong W H,Kong A.Correlation Structure and Convergence Rate of the Gibbs Sampler with Various Scans[J].J R Statist Soc B,1995,(57).

[3]Reiss R D.Approximate Distributions of Order Statistics[M].New York:Springer,1980.

[4]Whittaker J.Graphical Models in Applied Multivariate Statistics[M].Wiley:Chichester,1990.

[5]李开灿,孟朝玲.χ2分布、t分布和F分布的一致渐进正态性[J].北京印刷学院学报,2004,12(3).

[6]金秀岩.广义Γ分布的Pearson-χ2距离及其渐近性[J].西南师范大学学报:自然科学版,2008,33(4).

[7]李开灿.Pearson-χ2距离的若干性质[J].数学的实践与认识，2003,33（1）.