两参数Weibull分布基于BLUE的异常数据检验

王蓉华，徐晓岭，顾蓓青

0 引言

所谓异常数据通常是指一批数据中的个别者，其值明显地偏离该批数据中的其余值。目前，对多个异常数据的检验方法有两种：一是称之为群组检验，就是一次可检验多个异常数据，此检验的关键是要确定异常数据的个数；二是称之为逐步检验，就是每次只检验一个数据是否为异常数据，逐步排除，直至检验到正常数据为止。鉴于两参数Weibull分布在可靠性工程中重要的应用地位，下面简单介绍几种目前常用的针对两参数Weibull分布异常数据的检验方法。

文献[1]提出了一种利用G型统计量的检验方法，文献[2]对此作了改进并提出了F型统计量来检验异常大值。文献[3]提出了均值比检验方法，为确定异常数据的个数，定义了跳跃度的概念。文献[4]提出了一种新的检验异常大值的XLD统计量与检验异常小的XLX统计量。文献[5]推广了F-型检验，为确定异常数据的个数，还定义了灵敏度的概念。Weibull分布异常数据的检验方法很多。值得指出的是针对指数分布，文献[6]基于样本中位数提出一种检验方法，文献[7]作了进一步推广，但从单个样本分量出发构造检验统计量，方法虽然可行，但也浪费了许多可用的数据信息，这是因为异常数据的个数应该是少数几个，样本数据中的大部分还应该是正常数据，而且如果异常数据比较多，用简单的剔除并不合适，而应该考虑其他模型，例如混合模型等。

本文针对两参数Weibull分布，基于参数的最佳线性无偏估计（BLUE），给出一种新的异常数据的检验方法。

其中，m称为形状参数，η称为刻度参数。

从产品中任意取n个进行寿命试验，到有r个失效时试验停止（定数截尾寿命试验），失效时间依次为：X(1)≤X(2)≤…≤X(r)，其相应的次序观察值为：x(1)≤x(2)≤…≤x(r)。

由于系数C(n，r，j)，j=1，2，…，r并不相等，于是对于参数σ的最佳线性无偏估计而言，各 X(1)，X(2)，…，X(n)对参数σ的估计所起的作用是不一样的。为此针对参数σ的最佳线性无偏估计，定义各次序统计量的贡献率为：

1 两参数Weibull分布参数BLUE系数的特征

设产品的寿命为X，其服从两参数Weibull分布，分

其中，ρj表示次序统计量X(j)的贡献率。

考虑到系数C(n，r，j)，j=1，2，…，r的正负号，如是正号，对应的贡献率称为正贡献率；如是负号，对应的贡献率称为负贡献率。

仔细观察系数 C(n，r，j)，j=1，2，…，r 发现有如下特且给定 n，r后系数 C(n，r，j)，j=1，2，…，r 中 第 一 个 大 于 0 所 对 应 的j0，即C(n，r，j)＜0，j=1，2，…，j0-1 ，而 C(n，r，j)＞0，j=j0，j0+征（仅针对样本容量n=2(1)25）：

特征二：对于C(n，r，i)，i=1，2，…，j0，总存在 i0＜j0，是严格单调减少的。

特征三：对于C(n，r，i)，i=j0+1，j0+2，…，r，有：

C(n，r，j0+1)＜C(n，r，j0+2)＜…＜C(n，r，r)

其中，C(n，r，r) 比 C(n，r，i)，i=j0+1，j0+2，…，r-1有大幅度提高，也即X(r)的正贡献率最大。

2 异常数据检验

若样本数据仅存在极小异常值，且异常值的个数不超过 i0个，即异常小数据存在于 X(1)，X(2)，…，X(i0)中，由于C(n，r，j)＜0，j=1，2，…，i0，易见参数 σ 的最佳线性无偏

如果样本数据存在异常值，则其必将影响到参数的估计。事实上，若样本数据仅存在极大异常值，且异常值的个数不超过r-j0+1个，即异常大数据存在于X(j0)，X(j0+1)，…，X(r)中，由于 C(n，r，j)＞0，j=j0，j0+1，…，值的个数至少为i0+1个，由于X(i0)的负贡献率最大，是一个转折点，于是可以认为是两个不同总体的混合，即采用混合模型处理。

若样本数据同时存在极大异常值与极小异常值，且极大异常值的个数不超过r-j0+1个，即异常大数据存在于如果异常大值的个数至少为r-j0+2个，异常小值的个数至少为i0+1个，于是可以认为是三个不同总体的混合，即

步骤2：构造检验统计量Tj0=采用混合模型处理。

异常数据检验的关键问题之一是确定异常数据的个数，鉴于上述讨论，在此可以认为异常数据的最多疑似个数为i0+(r-j0+1)个，其中有i0个是疑似极小异常值，即X(1)，X(2)，…，X(i0)，r-j0+1个是疑似极大异常值，即 X(j0)，X(j0+1)，…，X(r)。或者说非异常的样本数据有 j0-i0-1个，即 X(i0+1)，X(i0+2)，…，X(j0-1)。

由此，针对定数截尾两参数Weibull分布异常数据检验分为如下三种场合，其检验步骤如下（给定显著性水平α）：

场合一：如果只存在极大异常值

记由次序统计量 X(1)，X(2)，…，X(k)所得的参数σ的最佳线性无偏估计（BLUE）为 σ̂n，k(X(1)，X(2)，…，X(k)) ，即：分布与参数无关。事实上，易见Tj0的分布与参数无关。同时有Tj0对X(j0)严格单调增加。记统计量Tj0的观察值为tj0，而记Tj0的分布的上侧α分位数为Tj0(α)。给定样本容量n以及 j0、显著性水平α，通过10000次Monte-Carlo模拟得到统计量Tj0的上侧α分数，结果见下页表1。

若tj0＜Tj0(α)，则认为 X(j0)不是极大异常值，检验转入步骤3。

步骤3：构造检验统计量Tj0+1=，其分布与参数无关，且对 X(j0)严格单调增加。

若 tj0+1≥Tj0+1(α)，则认为 X(j0+1)为极大异常值，进而认为 X(j0+2)，X(j0+3)，…，X(r)均为极大异常值，终止检验。

若 tj0+1＜Tj0+1(α)，则认为 X(j0+1)不是极大异常值，检验转入下一步骤。

如此下去，直至某一步终止检验。

如果一直没有终止检验，则最后所构造的检验统计量为：

表1 Tj0分布的上侧分位数表

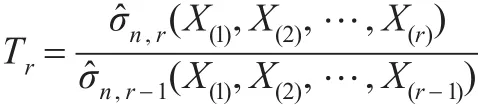
若tr≥Tr(α)，则认为X(r)为极大异常值，而X(j0)，X(j0+1)，…，X(r-1)都不是极大异常值。

若tr＜Tr(α)，则认为X(r)不是极大异常值，也就是说整个样本数据不存在极大异常值。

场合二：如果只存在极小异常值

记由次序统计量X(k)，X(k+1)，…，X(r)所得的参数σ的最佳线性无偏估计（BLUE）为σ̂n，k(X(k)，X(k+1)，…，X(r))，即：C(n，k，j)为左截尾的BLUE系数。

步骤 1：计算σ̂n，i0(X(i0)，X(i0+1)，…，X(r)) ，σ̂n，i0+1(X(i0+1)，X(i0+2)，…，X(r))

步骤2：构造检验统计量Ti0分布与参数无关，且对X(i0)严格单调减少。记统计量Ti0的观察值为ti0，而记Ti0的分布的上侧α分位数为Ti0(α)。

若ti0≥Ti0(α)，则认为X(i0)为极小异常值，进而认为X(1)，X(2)，…，X(i0-1)均为极小异常值，终止检验。

若ti0＜Ti0(α)，则认为X(i0)不是极小异常值，检验转入步骤3。

步骤3：构造检验统计量Ti0-1布与参数无关，且对X(i0-1)严格单调减少。

若ti0-1≥Ti0-1(α) ，则 认 为X(i0-1)为极小异常值，进而认为X(1)，X(2)，…，X(i0-2)均 为 极 小 异 常值，终止检验。

若ti0-1＜Ti0-1(α) ，则 认 为X(i0-1)不是极小异常值，检验转入下一步骤。

如此下去，直至某一步终止检验。

如果一直没有终止检验，则最后所构造的检验统计量为：

若t1≥T1(α)，则认为X(1)为极小异常值，而X(2)，X(3)，…，X(i0)都不是极小异常值。

若t1＜T1(α)，则认为X(1)不是极小异常值，也就是说整个样本数据不存在极小异常值。

场合三：如果既存在极大异常值，又存在极小异常值

从j0-i0-1个非异常的样本数据X(i0+1)，X(i0+2)，…，X(j0-1)出发，分别向两个方向检验极大异常值与极小异常值。记由次序统计量X(k+1)，X(k+2)，…，X(s-1)所得的参数σ的最佳线性无偏估计（BLUE）为σ̂n，k+1，s-1(X(k+1)，X(k+2)，…，X(s-1))，即：

而此处的C(n，k+1，s-1，j)为双边截尾的BLUE系数。

检验极大异常值如下：

步骤1：计算 σ̂n，i0+1，j0(X(i0+1)，X(i0+2)，…，X(j0))，σ̂n，i0+1，j0-1(X(i0+1)，X(i0+2)，…，X(j0-1))

步骤2：构造检验统计量Tj0=且对X(j0)严格单调增加。记统计量Tj0的观察值为tj0，而记Tj0的分布的上侧α分位数为Tj0(α)。

若 tj0≥Tj0(α)，则认为 X(j0)为极大异常值，进而认为X(j0+1)，X(j0+2)，…，X(r)均为极大异常值，终止检验。

若tj0＜Tj0(α)，则认为 X(j0)不是极大异常值，检验转入步骤3。

步骤3：构造检验统计量Tj0+1=且对X(j0+1)严格单调增加。

若 tj0+1≥Tj0+1(α)，则认为 X(j0+1)为极大异常值，进而认为 X(j0+2)，X(j0+3)，…，X(r)均为极大异常值，终止检验。

若 tj0+1＜Tj0+1(α)，则认为 X(j0+1)不是极大异常值，检验转入下一步骤。

如此下去，直至某一步终止检验。

如果一直没有终止检验，则最后所构造的检验统计量为：

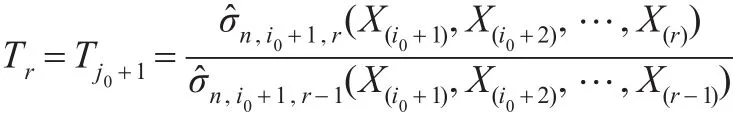
若 tr≥Tr(α)，则认为X(r)为极大异常值，而X(j0)，X(j0+1)，…，X(r-1)都不是极大异常值。

若tr＜Tr(α)，则认为 X(r)不是极大异常值，也就是说整个样本数据不存在极大异常值。

检验极小异常值如下：

步骤1：计算 σ̂n，i0，j0-1(X(i0)，X(i0+1)，…，X(j0-1))，σ̂n，i0+1，j0-1(X(i0+1)，X(i0+2)，…，X(j0-1))

步骤2：构造检验统计量Ti0=且对X(i0)严格单调减少。记统计量Ti0的观察值为ti0，而记Ti0的分布的上侧α分位数为Ti0(α)。

若ti0≥Ti0(α)，则认为 X(i0)为极小异常值，进而认为X(1)，X(2)，…，X(i0-1)均为极小异常值，终止检验。

若ti0＜Ti0(α)，则认为 X(i0)不是极小异常值，检验转入步骤3。

步骤3：构造检验统计量Ti0-1=对X(i0-1)严格单调减少。

若 ti0-1≥Ti0-1(α)，则认为 X(i0-1)为极小异常值，进而认为 X(1)，X(2)，…，X(i0-2)均为极小异常值，终止检验。

若 ti0-1＜Ti0-1(α)，则认为 X(i0-1)不是极小异常值，检验转入下一步骤。

如此下去，直至某一步终止检验。

如果一直没有终止检验，则最后所构造的检验统计量为：

若 t1≥T1(α) ，则 认 为 X(1)为 极 小 异 常 值 ，而X(2)，X(3)，…，X(i0)都不是极小异常值。

若t1＜T1(α)，则认为 X(1)不是极小异常值，也就是说整个样本数据不存在极小异常值。

3 算例分析

本文仅针对场合一（只存在极大异常值）通过算例分析来说明本文方法的应用。

例1[6]：取 n=r=16 ，x(1)，x(2)，…，x(14)来自标准指数分布（这14个数据见GB8056-87），并混入另两个数据x(15)，x(16)。16个样本数据如下：

0.0667 ，0.1381，0.2150，0.2984，0.3893，0.4893，0.6004，0.7254，0.8682，1.0349，1.2349，1.4849，1.8182，2.3182，8.0411，8.0914

当 n=r=16 时，j0=12，Tj0(α)=Tj0(0.05)=1.2424 ，而Tj0的观测值 tj0=1.0244＜Tj0(α)，不能说明 X(12)为极大异常值，进入下一步检验。

Tj0+1(α)=1.2113, 观 测 值tj0+1=1.0194＜Tj0+1(α)=1.2113,不能说明X(13)为极大异常值。进入下一步检验，Tj0+2(α)=1.1928 ，观测值 tj0+2=1.0267＜Tj0+2(α)=1.1928 ，不能说明 X(14)为极大异常值，进入下一步检验。Tj0+3(α)=1.1887 ，观测值 tj0+3=1.3738＞Tj0+3(α)=1.1887 ，则X(15)为极大异常值，进而X(16)也为极大异常值。

例2[9]：XXX飞机自上世纪70年代末装备部队以来，其飞机主要承力构件机翼的疲劳、腐蚀等耗损问题日益突出，个别机翼或因断裂而导致飞机事故，或因有裂纹而报废。经过多年的使用和部队、翻修厂的普查，已经积累一些裂纹尺寸、形状与飞机时间相关的数据以及失效机翼主梁的寿命数据。如何分析并处理这些数据，掌握它的分布情况，对确定主梁的疲劳寿命具有非常重要的意义。

航空工程上通常将材料的疲劳寿命认为是对数正态分布或者是Weibull分布，那么针对机翼主梁寿命更接近实际情况呢？XXX在使用过程中积累的主梁断裂数据有限，所以采用本文的小样本场合的拟合检验。文献[9]给出了样本容量为8的全样本数据如下：

2865.28 ，2895.12，2895.2，2918.31，3077.52，3105.37，3127.12，3146.01

当 n=r=8时，j0=7，Tj0(α)=Tj0(0.05)=1.5398而 Tj0常值。

4 总结

所谓异常数据通常是指一批数据中的个别者，其值明显地偏离该批数据中的其余值。目前关于异常数据检验的难点主要是两个，一是如何确定异常数据的个数，二是构造合适的检验统计量。

本文针对样本数据服从两参数Weibull分布，定数截尾样本中出现异常数据的检验问题。从寿命X服从两参数Weibull分布（形状参数为m，刻度参数为η）的产品中任意取n个进行寿命试验，到有r个失效时试验停止（定数截尾寿命试验），失效时间依次为：X(1)≤X(2)≤…≤X(r)，其相应的次序观察值为：x(1)≤x(2)≤…≤x(r)。参数 σj)lnX(j)。由于各 X(1)，X(2)，…，X(n)对参数 σ 的估计所起的作用是不一样的，为此本文定义了各次序统计量的贡献率。依据贡献率的分析给出了异常数据的疑似个数，在此基础上，基于参数σ的最佳线性无偏估计（BLUE）构造了异常数据的检验统计量，为方便实际工作者的应用，通过Monte Carlo模拟给出了检验统计量分布的分位数。最后通过两个应用实例说明本文所给出的方法是切实可行的。

[2]费鹤良,陆向薇,徐晓岭.极值分布和威布尔分布异常数据的检验方法[J].应用数学学报，1998，21（4）.

[3]王蓉华,费鹤良,徐晓岭.异常数据检验的均值比方法[J].数理统计与应用概率，1998，13（1）.

[4]徐晓岭,王蓉华.Weiull分布异常数据检验[J].数理统计与应用概率，1996，11（2）.

[5]王蓉华,徐晓岭.全国第五届可靠性学术会议论文集[M].北京:机械工业出版社，1995.

[6]朱宏.指数分布样本多个异常数据的检测[J].电子学报，1994，22（12）.

[7]田存志,张进,王学仁.指数分布中下异常值的逐步检验的改进[J].数理统计与应用概率，1998，13（1）.

[8]中国电子技术标准化研究所.可靠性试验用表（增订本）[M].北京:国防工业出版社,1987.

[9]宣建光,马康民.XXX机翼主梁的寿命分布研究[J].强度与环境，2000,（4）.