各向异性半椭圆型波导对平面波的电磁散射
毛仕春, 吴振森, 张兆慧, 高剑森
(1.宿迁学院 信息工程学院, 江苏 宿迁 223800; 2.西安电子科技大学 物理与光电工程学院, 陕西 西安 710071)
0 引言
近年来,随着各向异性材料介质在高灵敏度天线的研制开发,以及在各种高性能电子器件等领域的广泛应用,使其与电磁波之间的特性成为众多学者研究的热点[1-3].研究成果中,许多文献讨论了圆柱体或者椭圆柱体对平面波的散射问题[4-7].也有学者对于半椭圆柱嵌入导体时的散射特性进行了分析讨论[8-9],但文献中仅仅探讨了半椭圆柱体为各向同性介质材料时的电磁特性,对于柱体为均匀各向异性介质材料未有涉及.柱体为各向异性介质材料时,半椭圆柱波导嵌入导体基底的电磁特性对于开发和研制相关器件有一定的参考价值.
本文讨论了横截面为半椭圆型各向异性介质柱体波导嵌入到导体时对平面波的电磁散射.由于在椭圆柱体边界,其切向分量和法向分量并不正交,所以角向马丢函数的正交关系无法应用到推导过程中,为此,通过积分方法(Galerkin’s Method)对边界条件进行了处理,最终将散射场和柱体内场的待定系数求解出来.本文仅讨论入射波为横磁波入射的情形,此时在导体基底上切向分量即电场强度为0,以此方法可以较方便的推导出横电波入射的情形.为描述问题方便,时谐因子exp(jωt)不再标出.
1 理论
如图1所示,横截面为椭圆的无限长均匀各向异性柱体,其下半椭圆截面嵌入到导体内,一束TM平面波以相对于x轴呈θi入射到柱体上.平面直角坐标系(x,y)与平面椭圆柱坐标系(u,v)具有如下关系:
x=dcoshucosv
(1)
y=dsinhusinv
(2)
其中d表示椭圆的半焦距,a与b分别表示半长轴和半短轴.
在平面直角坐标系中,描述均匀各向异性介质椭圆柱体(区域II部分)的电容率和磁导率分别为:
(3)
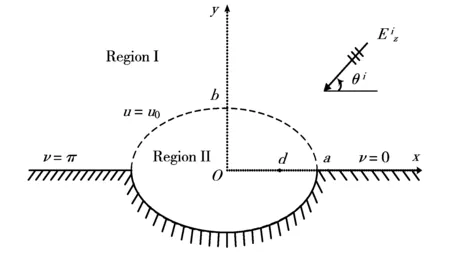
图1 半椭圆波导截面示意图
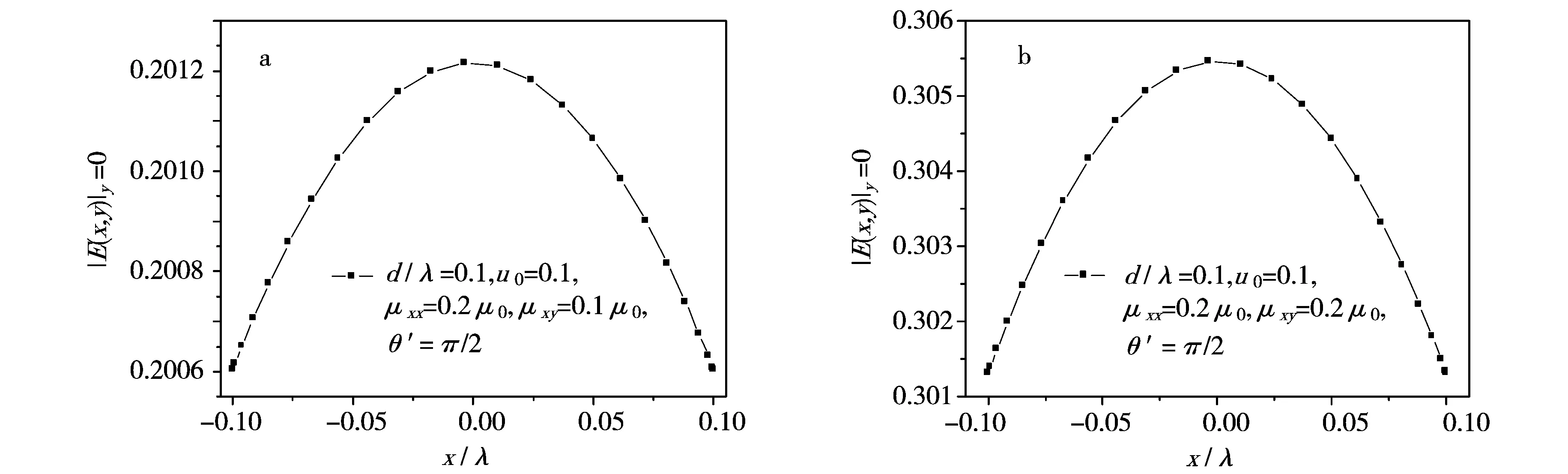
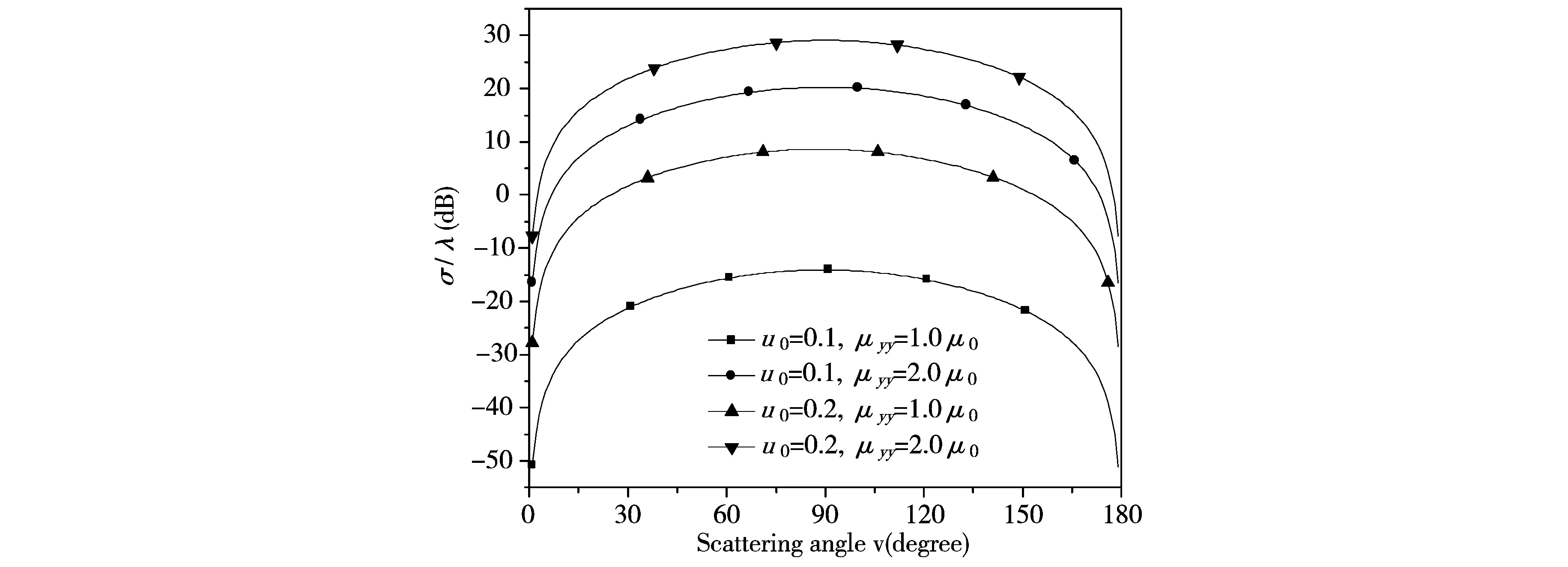
当入射平面波以θi角入射到导体基底上时,由于导体表面对平面波的散射效应,在椭圆柱体内存在同时存在着导体对平面波的镜面反射波,散射波以及透射波.在区域I (u>u0,0 (4) (5) (6) 如前所述,区域I部分的电磁波为入射波、镜面反射波及散射波的叠加,即 (7) 在区域II(u 在上半椭圆柱与自由空间的界面上(0≤v<π,u=u0),椭圆柱内场在界面处的切向分量满足关系: (9) 其中 (10) (11) a=sinhucosv,b=coshusinv (12) (13) 同时,在区域I部分的电磁场在上述界面处(0≤v<π,u=u0)的切向分量满足 (14) 其中μ0表示自由空间的磁导率. 上述透射波以及散射波包含的待定系数需要通过边界条件进行确定,即 (15) Ez=0(π≤v<2π,u=u0) (16) (17) 经过整理,利用边界条件可以得到如下两方程组 (18) (19) 其中 (20) (21) (22) (23) (24) 上述公式中符号“D”表示马丢函数对变量u或者v的导数. 通过对上述方程组进行截断处理,可以同时求出待定系数g(θ)和h(θ),同时也可以将om求解出来.最后,单位长度的雷达散射截面可以表达为: (25) 图2给出了沿x轴方向的电磁波振幅的分布情况.从图中可以看出,由于此时入射波垂直入射到柱体上,所以波振幅相对于x轴对称分布.图3给出了沿y轴方向的电磁波振幅的分布情况. 图2 沿x轴方向电场强度振幅分布情况 图3 沿y轴方向电场强度振幅分布情况 图4 E极化波,双向雷达散射截面()dB. =0.2,θi=,μxx=2.0μ0,μxy=μyx=0,εzz=2.0ε0. 讨论了二维均匀各向异性半椭圆型波导对平面波的电磁散射,以横磁波入射为例进行了解析说明,且较容易推导到出横电波入射的情形.给出了椭圆截面沿x和y轴方向的电磁波振幅的分布情况,并讨论了当磁导率分量μyy以及椭圆截面形状变化对雷达散射截面的影响,数值结果对于新颖天线、波导的设计应用都有一定价值. [1] Richmond J H. Scattering by a ferrite-coated conducting sphere[J]. IEEE Trans Antennas Propagat, 1987,35(1): 73-79. [2] Gurwich I, Kleiman M, Shiloah N, et al. Scattering of electromagnetic radiation by multilayered spheroidal particles: recursive procedure[J]. Appl Opt, 2000,39(3): 470-477. [3] Beker B, Umashankar K R, Taflove A. Electromagnetic scattering by arbitrarily shaped two-dimensions perfectly conducting objects coated with homogeneous anisotropic materials[J]. Electromagnetics, 1990,10: 387-406. [4] Yeh C. The diffraction of waves by a penetrable ribbon[J]. J Math Phys, 1963,4: 65-71. [5] Ragheb H A, Shafai L. Electromagnetic scattering from a dielectric-coated elliptic cylinder[J]. Can J Phys, 1988, 66: 1115-1122. [6] Richmond J H. Scattering by a conducting elliptic cylinder with dielectric coating[J]. Radio Sci, 1988, 23: 1061-1066. [7] Caorsi S, Pastorino M. Scattering by multilayer isorefractive elliptic cylinder[J]. IEEE Trans Antennas Propagat, 2004, 52: 189-196. [8] Mao S C, Wu Z S. Scattering by an infinite homogenous anisotropic elliptic cylinder in terms of Mathieu functions and Fourier series[J]. J Opt Soc Am A, 2008,25(12): 2925-2931. [9] Mao S C, Cui L, Wu Z S. Scattering by a conducting elliptic cylinder coated with a nonconfocal homogeneous anisotropic shell[J]. Waves in Random and Complex Media, 2013, 23(4): 435-445.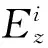

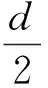
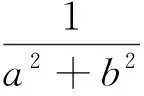

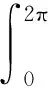
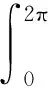


2 数值结果
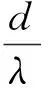


3 结束语

