异质环境中西尼罗河病毒稳态问题解的存在唯一性

葛 静

(淮阴师范学院 数学科学学院, 江苏 淮安 223300)

0 引言

考虑到蚊子和鸟都有空间扩散的特点,Lin等[1]研究了如下均质环境下西尼罗河病毒的自由边界问题

(1)

早期传染病研究通常假设环境是均质的, 所研究的模型多数是仅与时间有关的常微分系统[2-3], 随着研究的不断深入人们渐渐意识到空间扩散和环境异质性对疾病传播有重要的影响[4-6]. 相对于蚊子而言, 鸟类的扩散受环境影响较为显著,仅仅考虑恢复率γh以及死亡率dh和空间x相关. 而且由于蚊子的活动范围相对鸟的活动范围要小得多,可以忽略不计, 本文主要考虑如下西尼罗河病毒模型:

(2)

1 稳态问题解的存在唯一性

考虑问题(2)相应的稳态问题

(3)

接下来,求其平衡解, 由式(3)第中的第1个方程得

再将上式代入式(3)的第2个方程得

于是将方程简化为

(4)

由变分法可得模型(2)的基本再生数

容易证明如下性质, 参见文[2,3,7].

引理1 1-R0与λ1具有相同的符号,其中λ1为如下椭圆问题的主特征值

这里ψ(x)>0,x∈Ω为λ1相应的特征函数.由上述R0的定义以及[4]中的引理可得如下结论.

2 结论

定理1 关于R0下列性质成立.

(a)R0为正数, 且关于Dh是单调递减的;

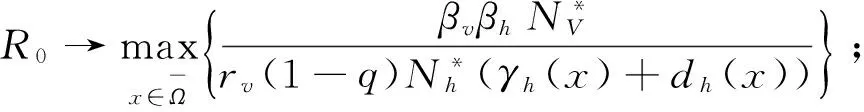
下面将依据阈值R0讨论问题(2)的稳态解的存在唯一性.

定理2 如下论断成立.

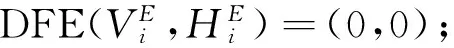
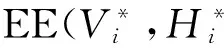
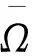
从而

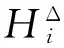
对上述不等式两边在x∈Ω上积分得

而不等式右边

故

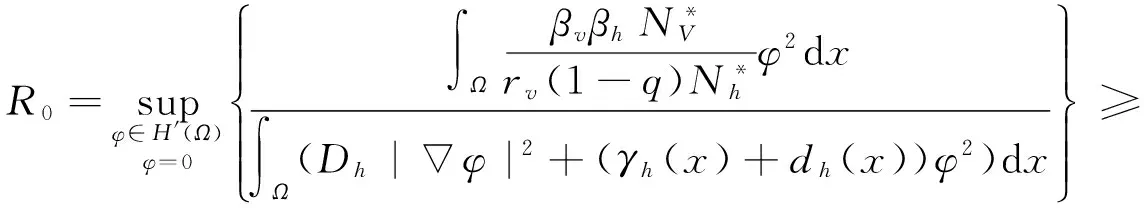
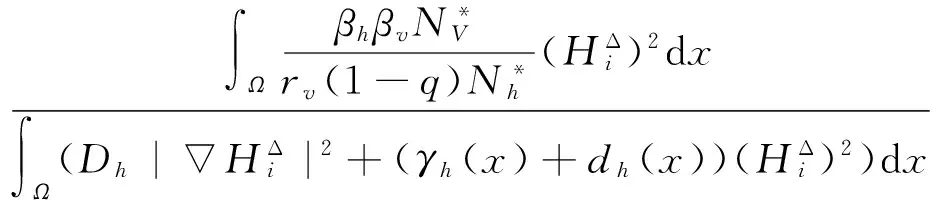
这与条件R0≤1矛盾, 故非负平衡点只有DFE.

下面证(ii), 当R0>1, 由引理1可知1-R0<0, 则如下特征问题

要保证εψ是问题(4)的下解, 只需

即只要

亦即

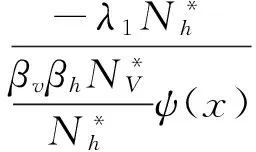
因为‖ψ‖L∞(Ω)=1, 故取

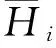
最后用乘乘减积技巧证明染病平衡点的唯一性.

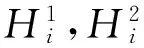
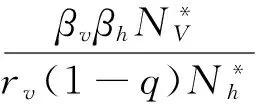
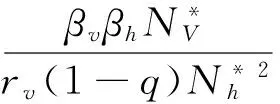
(5)

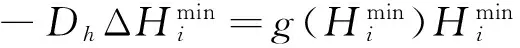
(6)

式(5)～(6)得

(7)

且在Ω上对式(7)两端分别积分有

[1] Lin Z G, Zhu H P. Spatial spreading model and dynamics of West Nile virus in birds and mosquitoes with free boundary[J].J Math Biol,2017,75(6-7):1381-1409.

[2] Jiang J F, Qiu Z P, Wu J H, et al. Threshold conditions for West Nile virus outbreaks[J].Bull Math Biol,2009,71(3),627-647.

[3] Fan G H, Liu J L, Driessche P vanden, et al. The impact of maturation delay of mosquitoes on the transmission of West Nile virus[J].Math Biosci,2010,228(2):119-126.

[4] Allen L J S, Bolker B M, Lou Y, et al. Asymptotic profiles of the steady states for an SIS epidemic reaction-diffusion model[J].Discrete Contin,Dyn Syst Ser A,2008,21(1):1-20.

[5] Ge J, Kim K I, Lin Z G, et al. A SIS reaction-diffusion-advection model in a low-risk and high-risk domain[J].J Differential Equations, 2015,259(10):5486-5509.

[6] 林支桂. 张丹，宋燕，等.一类具有常数输入及饱和传染率的传染病模型[J].渤海大学学报(自然科学版)，2013，34(1)：8-15.

[7] 林支桂. 数学生态学导引[M].北京: 科学出版社, 2013.