W UMa型食双星GM Bootis测光研究*

杨 勇，张燕平，付建宁，苍天启

(北京师范大学天文系，北京 100875)

GM Boo(又称GSC 02016-00830，ROTSE1 J144 726.56 + 224 515.0)在ROSTE 巡天(2000)[1]中被证认为是一个食双星系统，并给出轨道周期是0.361 103 00 ± 0.000 017 87天以及V星等是12.230等。随后，Blattler和Diethelm(2001)*http://www.konkoly.hu/cgi-bin/IBVSpdf?5125对包括GM Boo在内的一些双星进行了CCD测光观测。他们获得了GM Boo的光变曲线，并且第1次给出了GM Boo的线性历元公式：

Min.I=HJD2 452 001.403 2+(0d.361 112)×E

(1)

文[2]利用ROTSE-I数据联合2MASS的J, H, K波段近红外数据从ROTSE-I中证认出1 022颗明亮的密近双星系统，并且给出了GM Boo的J-H色指数0.192，H-K色指数0.057，轨道周期0.361 112天以及日心距586 ± 7 pc。 文[3]认为GM Boo是一个W Ursae Majoris类型的密近双星，同时给出轨道周期是0.361 08天。

到目前为止，还没有任何对这颗食双星进一步详细的研究，从2010年到2015年，对这颗食双星进行了V和R两个波段的CCD测光观测，目的是分析GM Boo的轨道周期变化并得到它的测光轨道解。

1 观测和数据处理

从2010年5月16日到2015年2月3日，利用3台望远镜对GM Boo进行了共计16个夜晚的测光观测。其中，5个夜晚的数据是利用国家天文台兴隆观测站60 cm反射望远镜观测。该望远镜主焦点焦比F/4.23，有效视场18′ × 18′，位于主焦点的CCD像素1 024 × 1 024，像元分辨率1.056″/pixel。10个夜晚的数据是利用云南天文台的60 cm反射望远镜观测。该望远镜采用卡塞格林焦点，其焦比F/12.5，有效视场12′.5 × 12′.5，CCD型号Andor/s DW 436，CCD像素和像元分辨率分别2 048 × 2 048和0.37″/pixel。

仅有一个晚上的数据是利用位于美国新墨西哥州Tzec Maun望远镜远程观测。该望远镜是一台口径16英寸的反射望远镜，它的有效视场26′.1 × 17′.4，焦比F/9，CCD型号SBIG STL-6303，相应的像素和像元分辨率分别3 072 × 2 048和0.51″/pixel。测光观测日志见表1。图1展示了兴隆60 cm望远镜拍摄的一幅GM Boo图像。选择UCAC4 564-052034作为比较星和TYC 2016-1086-1作为校验星。表2列出了它们的坐标和V星等。利用IRAF程序对该双星的测光数据进行处理，主要过程包括减本底、除平场和孔径测光。

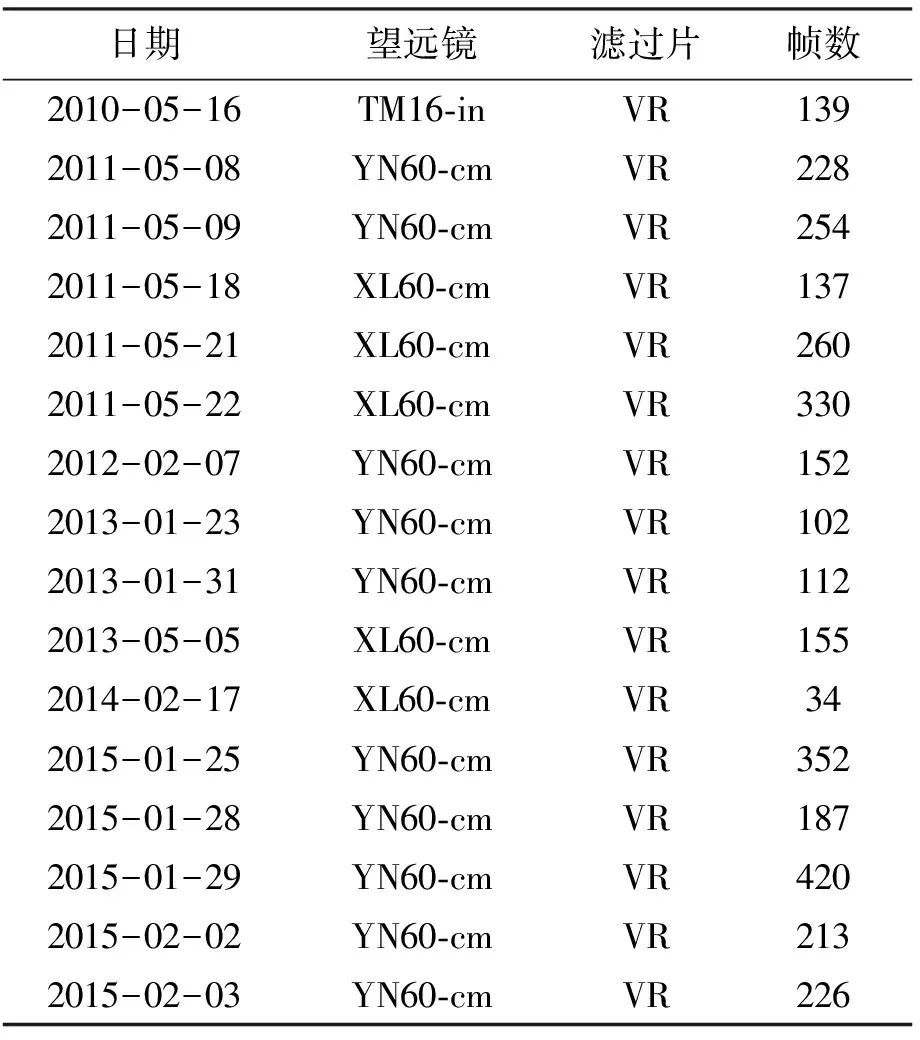
表1 GM Boo测光观测Table 1 Photometric observations of GM Boo

图1 兴隆60 cm望远镜观测的一幅GM Boo的CCD图像

Fig.1 A CCD image of GM Boo observed with the XL 60-cm telescope

表2 目标星、比较星和校验星的坐标和星等Table 2 Coordinates and magnitudes of the object, the check, and the comparison star

2012年5月14日，使用位于兴隆站的2.16 m望远镜获得了GM Boo的低色散光谱。该光谱是用BFOSC低色散光谱仪拍摄，其光栅为G7，狭缝宽度为1.8″，线色散为95 mm，中心波长为530 nm，波长范围为380～680 nm。利用IRAF程序对原始光谱数据进行了处理，得到该双星低分辨率的光谱(见图2)。与Pickles光谱流量库[4]进行对比，GM Boo的光谱类型初步被证认为是F3V～F5V，温度范围约为6 800～7 000 K。

图2 兴隆2.16 m望远镜观测的GM Boo光谱
Fig.2 The spectrum of GM Boo observed with XL 2.16-m telescope

2 轨道周期变化

利用较差测光，提取了GM Boo所有的光变曲线。同时采用最小二乘法对光变极小值附近进行二次拟合，确定了19个新的极小值时刻。为了研究轨道周期的变化，从历史数据中收集了43个极小值时刻，所有极小值时刻列于表2。利用最小二乘法得到了GM Boo新的线性和二次历元公式：

Min.I=HJD2 455 332.900 7(3)+0d.361 118 63(7)×E，

(2)

Min.I=HJD2 455 332.900 5(2)+0d.361 119 3(1)×E+1d.05(2)×10-10×E2.

(3)

因此，根据新的线性和二次历元公式推导该双星的O-C值(观测和计算得到的极小值时刻之差)，列在表3。利用表3中的(O-C)1值和圈数E，描绘了GM Boo的O-C图(见图3)，目的是分析该双星长期的轨道周期变化。图3中，红色实心圆点代表本文的数据，黑色空心圆代表文献中的数据。通过对图3中所有数据点进行二次拟合，得到一个向上的抛物线，表明GM Boo的轨道周期正在增加。根据二次历元公式的二次项得到该双星轨道周期增加的速率是dP/dE=1.05 × 10-10d·cycle-1或dP/dt=1.06 × 10-7d·yr-1。相接双星轨道周期增加表明较小质量子星正在向较大质量子星进行物质转移[5]。

图3 GM Boo的O-C图。实点代表本文的数据，空心圆点代表文献中的数据。实线是对全部数据的二次拟合

Fig.3 O-C diagram of GM Boo. The solid points represent our data and the open circles represent the data from the literature. The solid curve shows the quadratic fitting

3 测光数据的轨道解

使用2015版的Wilson-Devinney(W-D)程序[6-9]获得GM Boo测光数据的轨道解。用于解轨的测光数据来自2011年兴隆60 cm望远镜观测的3天数据(见表1)，因为这3天数据质量相对较高。对这3天测光数据进行相位合并得到在V和R波段具有完整相位覆盖的光变曲线(见图4)。

GM Boo是被分类为W UMa类型的食双星[4]。因此，使用W-D程序的Mode 3(overcontact binary not in thermal contact)寻找轨道初解。根据GM Boo的光谱型是F3V～F5V，假设主星温度T1=6 900 K，取两子星的重力昏暗系数g1=g2=0.32[10]，两子星的热反照率A1=A2=0.50[11]，两子星的热临边昏暗系数和各个波段的临边昏暗系数从文[12]获得(见表3)。以上参量在解轨过程中固定不变。在W-D解轨过程中可以被调整的自由参量包括轨道倾角i，次星温度T2，两子星的表面势能Ω1和Ω2，两子星的质量比q=m2/m1，以及主星VR波段的相对单色光度。

图4 GM Boo的光变曲线。空心圆点代表观测数据，实线是理论光变曲线
Fig.4 Light curves of GM Boo. The open circles represent observational data and the solid lines show theoretical light curves1BBS=Bulletin der Bedeckungsveraenderlichen-Beobachter der Schweizerischen Astronomischen Gesellschaft.; BAVM=BAV- Mitteilungen (Berliner/Bundesdeutsche Arbeitsgemeinschaft für Veränderliche Sterne); IBVS=Information Bulletin on Variable Stars; OEJV=Open European Journal on Variable Stars; VSB=Variable Star Bulletin (Japan); JAAVSO=Journal of the American Association of Variable Star Observers

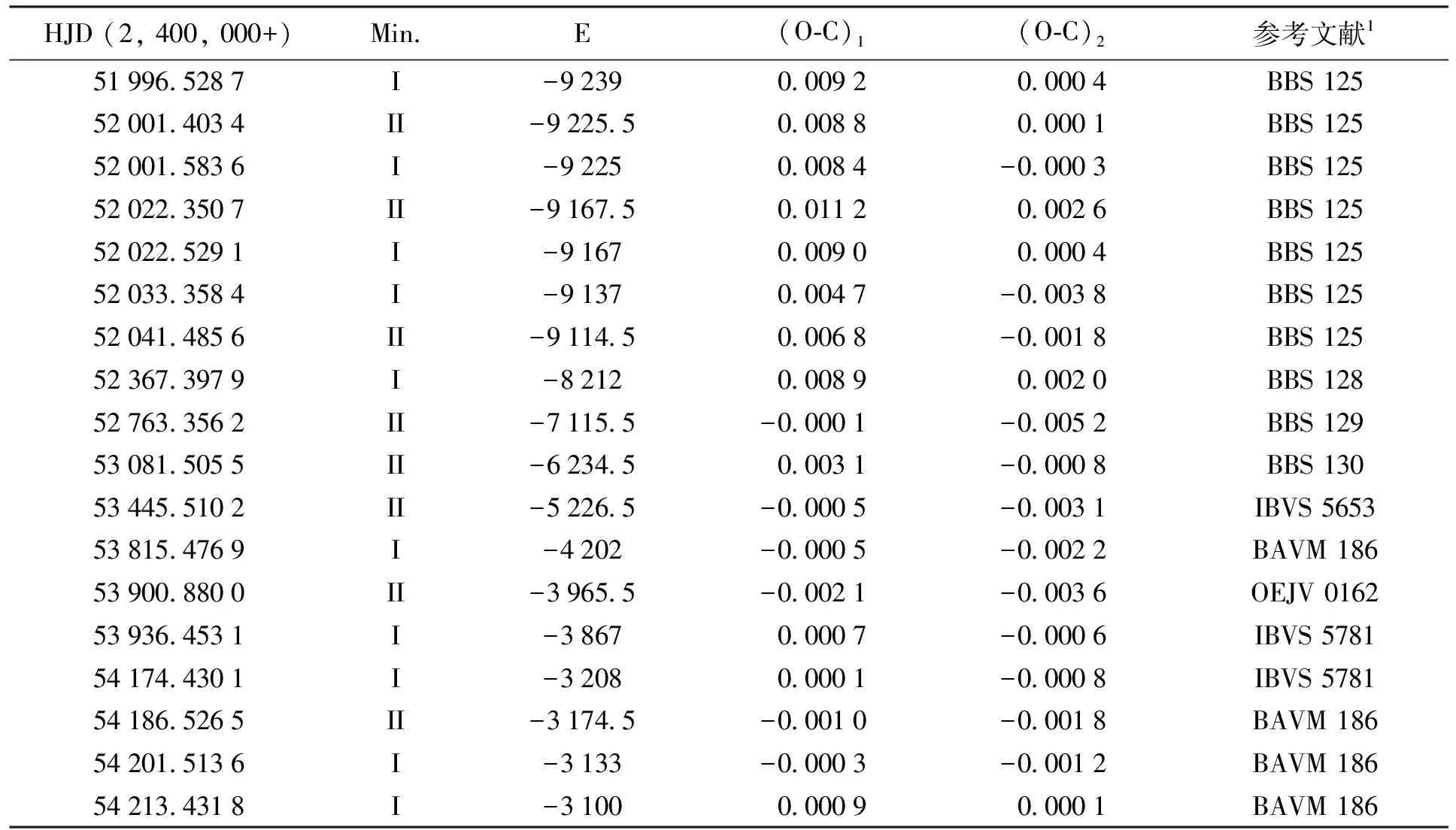
表3 GM Boo的极小值时刻和O-C值Table 3 Minimum times and O-C residuals of GM Boo

(续表3)

由于到目前为止没有任何关于该双星质量比(q=m2/m1)的信息，因此执行一个q-search的过程寻找最佳质量比。q-search的具体过程是选择一系列0.3到2之间的q值，间隔步长0.1，然后对每个q值分别执行W-D程序解轨，调整其它自由参量直到它们的校正值小于标准误差以及拟合光变曲线和观测的曲线之间残差σ达到最小值，最后对每个q值得到一个相应的残差σ。图5描绘了残差σ与质量比q之间的关系，在q=1.2处找到残差σ的最小值。因此，在q=1.2附近寻找最佳的质量比，放开q值进行微调，最终确定最佳的质量比q=1.22。最终的解轨结果揭示其质量小但温度更高的子星在主极小时被质量大的子星遮掩。因此，GM Boo是一个典型的W次型过相接双星系统[13]。

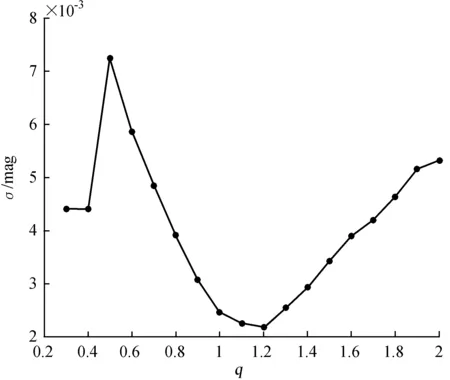
图5 残差σvs质量比q=m2/m1
Fig.5 The residualσversus mass ratioq=m2/m1

从图4光变曲线可以发现，位于相位0.25处的双星主极大光度比相位0.75处的次极大更暗，即存在O′Connell 效应*http://adsabs.harvard.edu/full/1951PRCO....2...85O。该效应代表在双星表面可能存在黑子或者亮斑。此处假设在大质量子星表面存在两颗黑子，然后调整黑子的经度、纬度、角半径和温度系数拟合光变极大值。最终得到最佳的测光数据的轨道解，列在表4。图4实线描绘了通过轨道解拟合得到的V和R波段理论光变曲线。GM Boo的几何结构如图6。

表4 GM Boo的轨道解Table 4 Orbital solution of GM Boo

Note:aAssumed

图6 相位0.0、0.25、0.5和0.75处GM Boo的几何结构
Fig.6 The geometry configurations of GM Boo at the phase 0.0, 0.25, 0.5 and 0.75, respectively

4 总结与讨论

通过CCD测光观测，获得了GM Boo 19个新的光变极小时刻，并推导出它的线性和二次历元公式。另外，通过与Blattler和Diethelm(2001)的光变曲线和历元公式进行对比发现，在本文的观测中，GM Boo的主极小和次极小时刻发生了反转，即光变主极小的相位对应Blattler和Diethelm光变次极小相位。类似的现象同样出现在Kepler卫星观测的部分食双星中[14]，该现象可能是由双星表面存在的黑子转移造成的。

在O-C图上展示了一个开口向上的抛物线，表明这十几年来GM Boo的轨道周期一直在增加，相应的周期增加速率是dP/dE=1.05 × 10-10d·cycle-1或dP/dt=1.06 × 10-7d·yr-1，这与近年来对相接双星周期变化研究的文[15-16]给出的结果相符。认为该双星周期增加可能是由于小质量伴星到大质量伴星之间存在物质转移，但是也不能完全排除第三体的存在，还需进一步的测光观测。

使用W-D程序获得了GM Boo的测光轨道解，并且因此确认了GM Boo是一个典型的W次型过相接双星系统。GM Boo两子星的表面势能是Ω1=Ω2=4.028 8(± 0.002 5)，利用f=(Ω-Ωin)/(Ωout-Ωin)，得出其填充因子f=11.11(± 0.39)%，即两子星相接度约为11%。根据GM Boo光变曲线极大值的不对称，表明存在O′Connell效应，利用W-D解轨得到在大质量伴星表面存在两个黑子。黑子的存在表明其表面有活跃的磁场活动，说明作为F型的恒星，与较晚型的恒星(G、 K型)一样，也存在较强的表面磁活动。

致谢：感谢兴隆2.16 m望远镜工作人员提供的支持。中国科学院国家天文台光学天文重点实验室的开放项目计划也对本文工作提供了部分支持。

[1] Akerlof C, Amrose S, Balsano R, et al. Rotse all-sky surveys for variable stars. I. test fields[J]. The Astronomical Journal, 2000, 119(4): 1901-1913.

[2] Gettel S J, Geske M T, McKay T A. A catalog of 1022 bright contact binary stars[J]. The Astronomical Journal, 2006, 131(1): 621-632.

[3] Hoffman D I, Harrison T E, McNamara B J. Automated variable star classification using the northern sky variability survey[J]. The Astronomical Journal, 2009, 138(2): 466-477.

[4] Pickles A J. A stellar spectral flux library: 1150-25000Å[J]. Publications of the Astronomical Society of the Pacific, 1998, 110(749): 863-878.

[5] Hoffman D I, Harrison T E, McNamara B J, et al. The case for third bodies as the cause of period changes in selected Algol systems[J]. The Astronomical Journal, 2006, 132(6): 2260-2267.

[6] Wilson R E, Devinney E J. Realization of accurate close-binary light curves: application to MR Cygni[J]. The Astrophysical Journal, 1971, 166: 605-619.

[7] Wilson R E. Accuracy and efficiency in the binary star reflection effect[J]. The Astrophysical Journal, 1990, 356: 613-622.

[8] Wilson R E. Binary star light-curve models[J]. Publications of the Astronomical Society of the Pacific, 1994, 106(703): 921-941.

[9] Wilson R E, Van Hamme W. Unification of binary star ephemeris solutions[J]. The Astrophysical Journal, 2013, 780(2): 151-167.

[10]Lucy L B. Gravity-darkening for stars with convective envelopes[J]. Zeitschrift für Astrophysik, 1967, 65: 89-92.

[11]Ruciński S M. The W UMa-type systems as contact binaries. I. two methods of geometrical elements determination. degree of contact[J]. Acta Astronomica, 1973, 23: 79-120.

[12]Van Hamme W. New limb-darkening coefficients for modeling binary star light curves[J]. The Astronomical Journal, 1993, 106: 2096-2117.

[13]Binnendijk L. The orbital elements of W Ursae Majoris systems[J]. Vistas in Astronomy, 1970, 12: 217-256.

[14]Tran K, Levine A, Rappaport S, et al. The anticorrelated nature of the primary and secondary eclipse timing variations for the kepler contact binaries[J]. The Astrophysical Journal, 2013, 774(1): 81-94.

[15]Qian S B, Li K, Liao W P, et al. The first photometric investigation of the neglected W-UMa-type binary star UZ CMi[J]. The Astronomical Journal, 2013, 145(4): 91-96.

[16]Qian S B, Liu N P, Liao W P, et al. First photometric investigation of the newly discovered W UMa-type binary star MR Com[J]. The Astronomical Journal, 2013, 146(146): 38-44.